基于“以学为中心”理念的格林公式的探究式教学∗

景慧丽 刘 华

(火箭军工程大学基础部，陕西 西安 710025)

0 引 言

格林公式是《高等数学》课程中的一个重点内容也是一个难点内容[1]，从形式上建立了平面有界闭区域上的二重积分和区域边界上的第二类平面曲线积分之间的联系，实质揭示的是函数在区域内部的取值规律和区域边界上的取值规律之间的联系，具有重要的理论价值和应用价值.其在多元函数积分学中最重要的应用之一是计算第二类平面曲线积分.但是在教学中大部分学生甚至是复习考研的学生使用格林公式时经常出错，甚至都不知道格林公式的使用条件.这是因为一方面格林公式确实是比较抽象，另一方面传统讲授法都是先复习牛顿—莱布尼茨公式[2]，再给出平面区域的分类及其边界曲线的正向定义，然后直接给出格林定理及其证明，最后再应用格林公式，所以大部分学生既记不住格林公式，更不理解格林公式的使用条件.为了帮助学生理解和熟记格林公式，并能正确地运用格林公式计算第二类平面曲线积分，笔者结合多年的教学实践，对这部分内容进行了探究式教学.

1 格林公式的教学过程

(1)强调联系性，提出问题，进行探索.

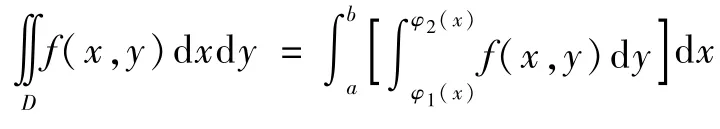
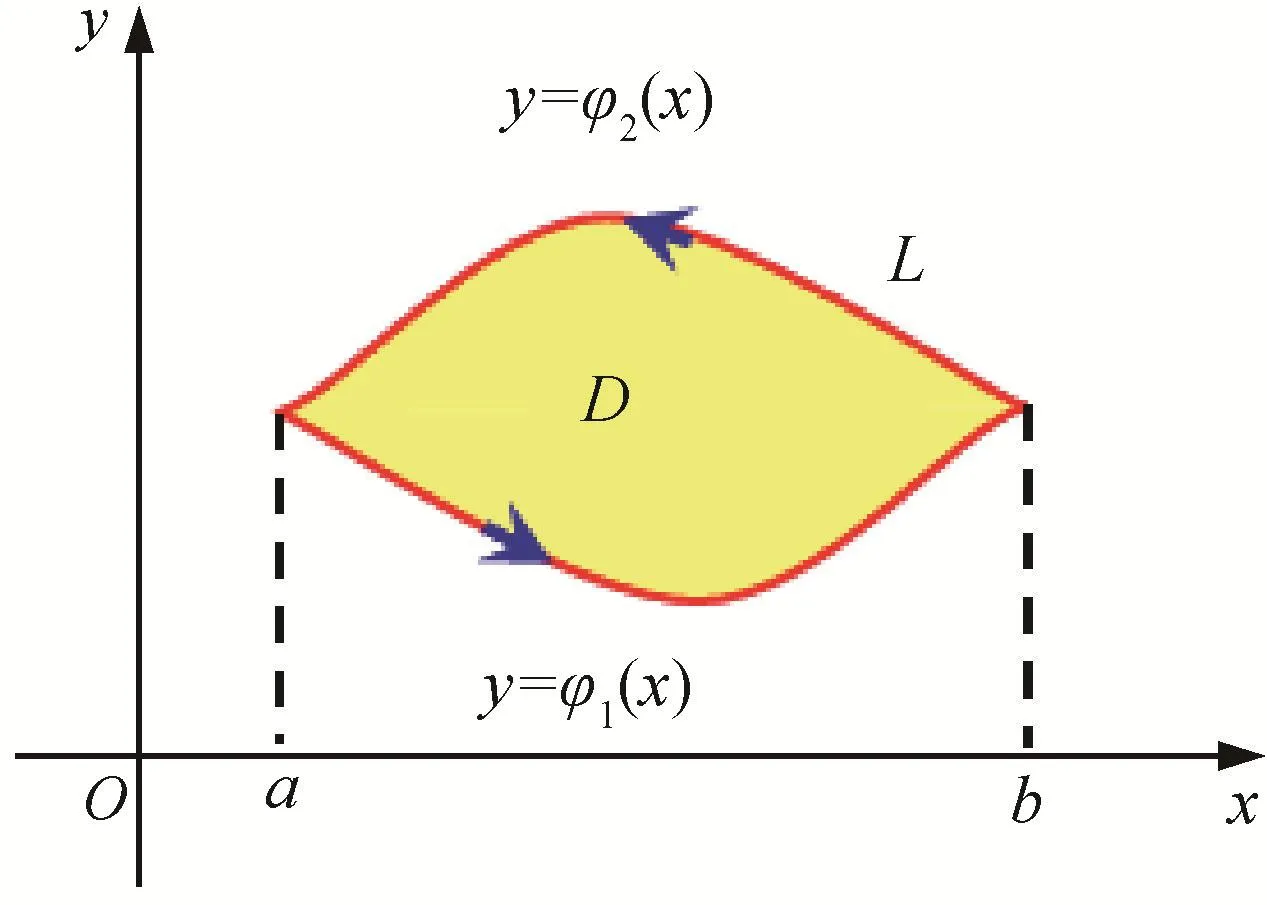
图1 X-型域

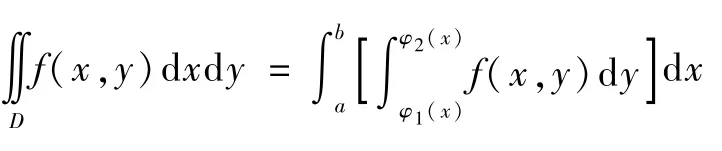
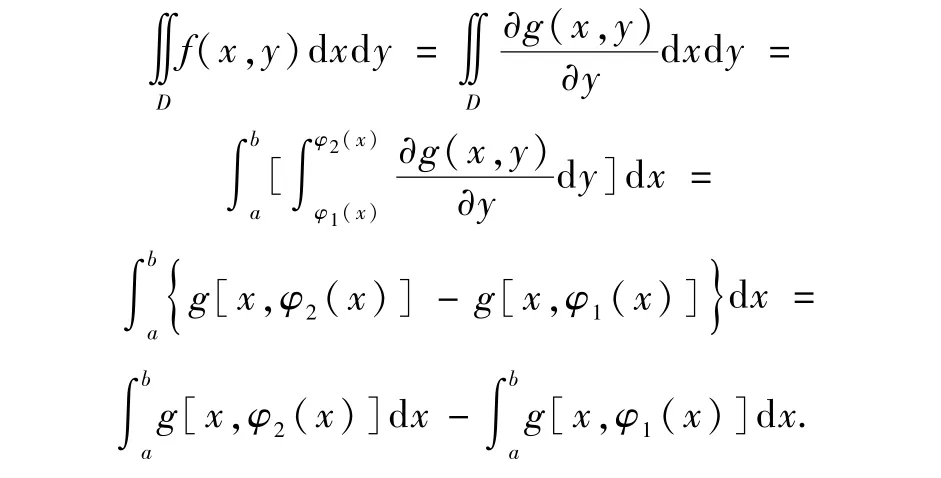
推导到这里，很容易发现并能总结出其间的关系，即:若令g(x，y)=P(x，y)， 则

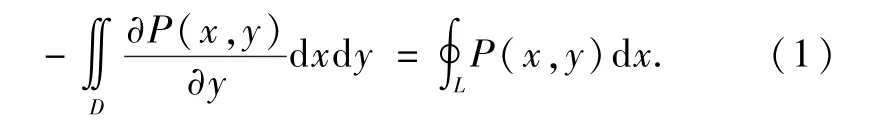
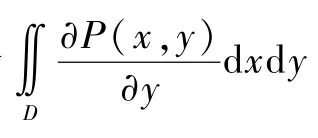
(2)大胆猜想，进行验证.

由于学生数学素养不同，接受新事物的能力也不同，所以存在猜想“五花八门”或“瞎猜胡猜”的现象.因此，强调“猜想”要建立在一定基础知识之上，通过观察、分析和实验等合情猜想.对猜想进行验证是让学生寻找方法对自己的猜想进行验证.最后进行总结，可以类比式(1)的获得过程，即把二重积分转化成定积分试试，并带领学生共同推导验证:

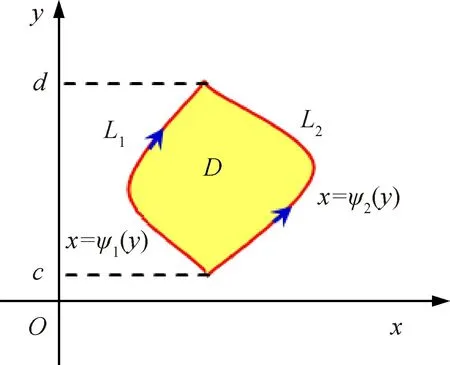
图2 Y-型域

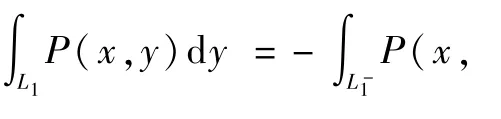
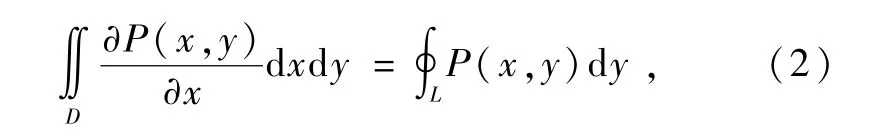
其中L是D的逆时针方向的边界曲线.

这个等式与大部分学生的猜想是不同的，是通过让学生总结式(2)成立的条件这种方法来解决学生的疑惑的.接下来需要把式(2)中的函数P(x，y)换成Q(x，y)，并没有直接替换，这是由于教材中第二类平面曲线积分的定义[1]是以 ∫LP(x，y)dx、∫LQ(x，y)dy形式给的，数学符号不要乱用，最好与教材符号保持一致，所以把式(2)中的函数P(x，y)换成Q(x，y)，即得等式

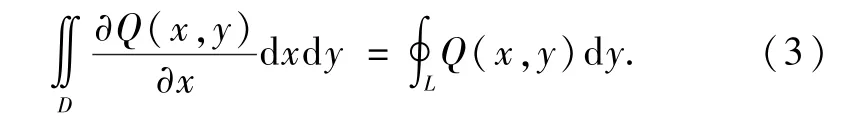
显然式(1)和(3)相加就是常用形式的格林公式，但是如果直接让式(2)相加，学生就会产生疑惑:为什么要相加?相加有什么意义呢?基于以上考虑，需先回忆第二类平面曲线积分的物理背景，然后了解其常见形式是∮LPdx+Qdy，观察式(1)和(3)，会发现2式右端相加刚好是∮LPdx+Qdy.此时，提出问题:2式能相加吗?相加的条件是什么?通过对上述问题的解答，并经过归纳总结就得到了下面的结论:

当区域D既是X-型域又是Y-型域，L是D的逆时针方向的边界线时，等式

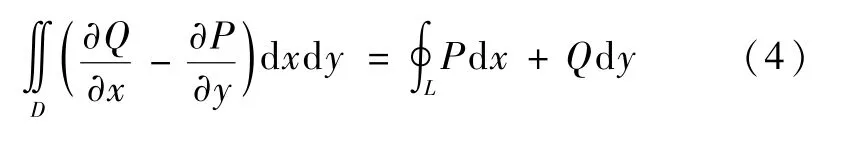
成立.

其实式(4)就是特殊单连通区域上的格林公式.即由平面上的有界闭区域并不都是这么特殊引出单连通区域和复连通区域的概念.这样就解决了学生的疑惑——为什么要讲这个概念，学生更容易理解和接受新知识.

(3)单、复连通区域及曲线正向见面.

在单、复连通区域的概念后，提出2个问题让学生思考、猜想:一般单连通区域和复连通区域上式(4)是否成立?如果L是D的顺时针方向的边界线，式(4)还成立吗?由此引出曲线正向的概念，这样就避免了一开始就给出该概念的突兀性.到此，所有准备工作完成，接下来就是证明式(4)在一般单连通区域及复连通区域上也是成立的.

(4)借助已知来研究未知，获取格林公式.

借助已知来研究未知是最常用的数学思想方法.数学研究问题的方法一般是从特殊到一般、从简单到复杂，引导学生很自然地想到先证明一般单连通区域的情形，启发学生把一般的转化成特殊的，这样很容易地完成此类区域的证明过程.对于复连通区域的证明，类比一般单连通区域的证明方法，把复连通区域转化成一般单连通区域来证明.但是部分学生不知道如何转化，是通过实物演示的方法来辅助分析的.另外，根据教学经验，部分学生会用大区域减去小区域这种错误的方法进行证明，因此用了故意出错的策略.

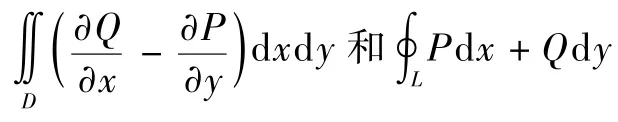
(5)揭示格林公式的本质，类比推广.

获得格林公式后，让学生从被积函数和积分域2个方面思考、总结公式所蕴含规律，从而揭示格林公式的本质.并让学生把格林公式和牛顿—莱布尼茨公式作比较，从而得到2个公式之间的关系，最后再类比这2个公式的本质，把这种思想推广到空间，这样既拓展了学生的知识又为后面的教学内容奠定了基础.

(6)应用格林公式，加深理解.

为了加深对格林公式的理解，精选下面的例题[4]:

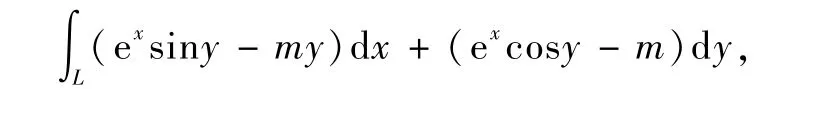
其中L是圆周x2+y2=ax(a＞0)的正向.

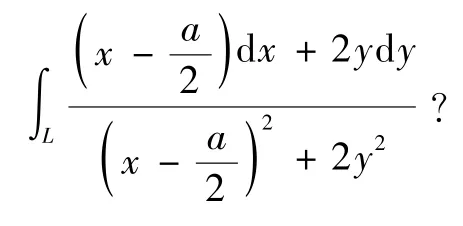
2 结束语

格林公式的探究式教学还原了知识的创建过程，融入了数学思想方法，有利于提升学生的数学素养.需要注意的是，在探究式教学中，教师是学生探索活动的设计者和探索过程中的引导者，如，在格林公式的教学中，式(1)的获得是探究式教学的关键和基础，运用了从特殊引导学生发现规律的策略.所以，要想充分发挥好探究式教学的优势，教师必须提高自身素质、熟悉教学内容、了解教学对象，这样才能充分发挥好自己的主导作用.