积累基本活动经验 发展数学核心素养——以一道例题教学片段为例

江苏省苏州市吴县中学 (215151) 吴海燕

《普通高中数学课程标准(2017年)》(下称《课程标准》)自颁布以来，引起了许多一线教师的关注与热议，大家最关心的是如何发展学生的数学核心素养.笔者在实践中认识到,积累基本活动经验不仅是“四基”的重要组成部分，也是学生提高“四能”、学会“三学会”的有效载体，更是学生发展数学核心素养的重要途径，对于实现课程目标具有重要的意义.下面笔者以一道例题教学片段为例，帮助学生正确解读和表征题目条件，运用数形结合、转化等数学思想来解决问题，提升学生解决圆锥曲线综合题的实战能力.以此来帮助学生积累基本活动经验，发展数学核心素养.

题目展示已知椭圆C的焦点为F1(-1,0)，F2(1,0)，过F2的直线与C交于A,B两点．若|AF2|=2|F2B|，|AB|=|BF1|，则C的方程为( ).

该题是2019年全国卷Ⅰ理科的第10题，涉及椭圆的标准方程、几何性质和直线与椭圆的位置关系等基础知识，难度中等偏上，题目叙述简洁入口宽，能有效甄别学生的思维能力，更是考察学科素养的良好素材，所以笔者决定和学生们共同解决.

1．亲历活动，获取基本活动经验

一位名人说过：我听过了，我就忘了；我看见了，我就记得了；我做过了，我就理解了.这句话道出了获取基本活动经验的重要性，学生在平时得到的经验往往是感性的、碎片化的，难以完善自身的知识认知结构，而经验性的认识往往是内隐的，这就需要我们教师设计、组织好每一个数学活动，以数学知识为载体，培养学生善观察、乐倾听、爱表达，会思辩的良好习惯，最终能使他们从感性认识上升到理性认识，并揭示出理性认识后的理性经验.

师：同学们，拿到一个解析几何问题，我们如何来审题？

生众：边阅读题目信息、边画出其示意图.

师：解析几何问题尽可能将文字语言转化为符号语言和图形语言.能交流一下这道题的想法吗？

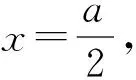
师：生1具有强烈的定义意识，轻松得出了各条线段的长度，定义法是解决圆锥曲线问题的重要方法，顺着生1的结果，大家能否根据题中的条件进行更深入的思考呢？

此时，教室里一片安静，同学们都在认真的思考和运算，5分钟后大部分同学都有了自己的想法，这时，生2的手举得高高的，于是让生2来说一下他的思路.只见生2不慌不忙走上讲台，一边口头表述，一边在黑板上板演.

图1

(写到这里生2似乎很兴奋)

师：生2能够抓住解析几何的本质—用代数的方法来研究解析几何问题，用向量知识将长度关系转化为坐标关系，结合方程组利用消元思想求解，整个求解过程体现了他较高的逻辑推理能力，较强的观察能力，变形能力和运算能力，虽然过程繁琐，但他还是顺利的到达了终点，让我们为生2这种坚韧不拔的精神点个赞(教室里响起了热烈的掌声).同学们!数学解题不仅是为了解决一个问题，更是培养我们一种契而不舍的精神，这对我们今后的学习和工作都是大有裨益的.那么这个题目还有别的思路吗？请同学们分组讨论一下.

学生们展开了热烈的讨论.一段时间过后，生3主动起来回答.

师：漂亮！生3先由线段关系发现点A的特殊性，而后迅速求出点B，再利用其在椭圆上得出了答案，快速简洁的求解得益于他较强的直观想象能力，这种数形结合的意识值得我们学习.还有别的解法吗？

说完，我便在黑板上画出了图2.这时，发现平时向来比较活泼的生4正眉头紧锁，若有所思地看着黑板上的图2，突然他兴奋地跳了起来，走上讲台，一边走一边喊：我有更简单的解法.

图2

图3

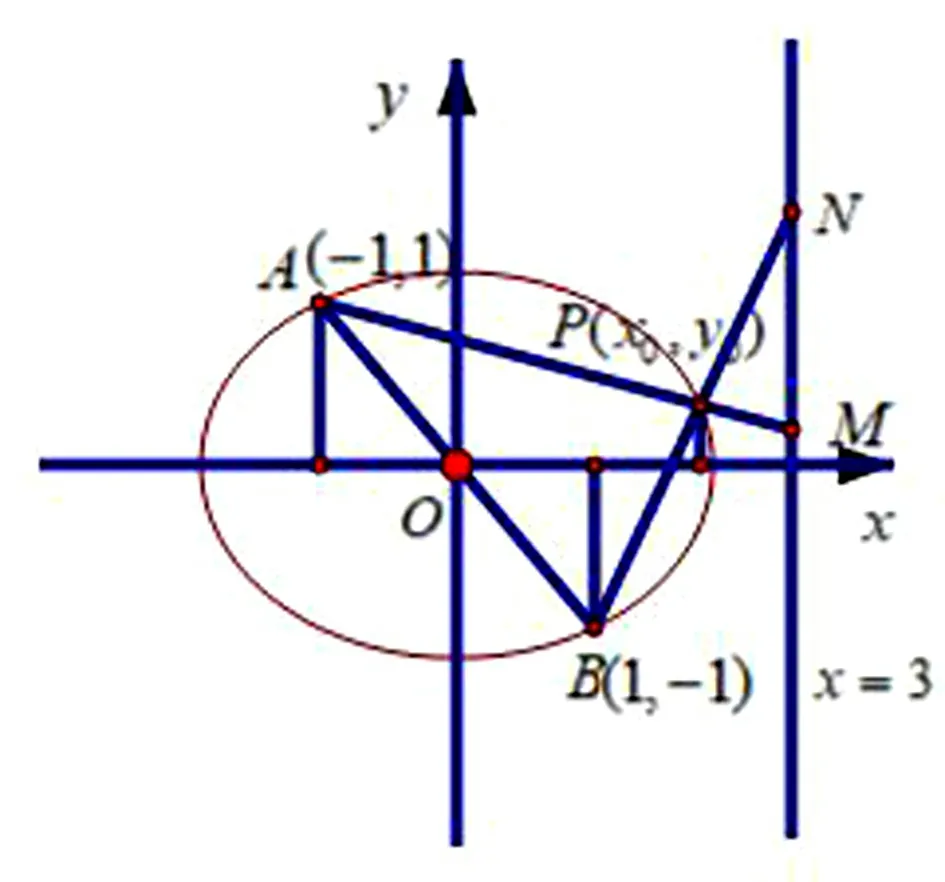
图4

基本活动经验的获取强调学生的主体性,学生只有通过自己亲身经历的活动经验才能更好地内化于心、外化于行,才能更好地发展数学核心素养.纵观整个课堂，教师鼓励学生自主探究、大胆陈述个人见解，引发学生进行充分的交流与真实的碰撞.在整个活动过程中，学从不同角度给出了试题的多种解法，而且通过在黑板上的讲、画结合的形式，给所有学生带来一种别样的解题体验，不仅使大家对题目的本质有了较清晰的认识，而且获取了几何直观助力代数推理和细致观察决定运算变形等基本活动经验，让直观想象、数学推理及数学运算等核心素养落地生根.

如果本题的教学仅限于止，学生则如“入宝山而空返”，收获的只是解决问题的基本经验，并未对解法的本质、各解法之间的比较等有更深层次的认识，不利于发展学生的数学核心素养.因此，需要教师帮助学生进一步提升基本活动经验.

2．主动反思，提升基本活动经验

学生经历或参与了数学活动并不是就能自动地获得充足的数学活动经验，它还需要学生主动地对活动过程进行反思、总结和交流，及时概括所获得的经验，使已得经验条理化和系统化.因此，教师应该引导学生对上述三个解法的由来、思维的过程以及运算的合理性等进行反思，让其体会到弄清问题，拟定计划在问题分析中的价值，养成批判性思维的习惯，以实现数学活动经验从低层次理解到高层次建构的生长.

师：同学们，刚刚我们用三种不同的方法解决了这个高考题，著名数学家波利亚提出的“怎样解题表”中“拟定计划”非常关键，它能清晰的展现解题的思维过程，大家能分别列出这三种方法的思维导图吗？经过大家的共同努力，学生们很快得出了结果.

解法一思维导图：

解法二思维导图：

排尿性晕厥又称小便猝倒，是指在排尿开始、排尿过程中或排完尿离开厕所时突然晕倒。主要是由于血管舒张和收缩障碍造成低血压，引起大脑一时供血不足所致。晕厥持续的时间，少则数秒钟，多则半小时，一般休息几个小时就会恢复正常，不会留下后遗症。排尿性晕厥多见于中老年男性，一般好发在夜间，常常突然发生，之前多无先兆。患有肺结核、神经衰弱和气血两虚的病人易发生此种晕厥。此外，病后体虚、过度疲劳以及饮酒等也可诱发这种现象。

解法三思维导图：

学生制作思维导图的过程是培养其自主、合作和探究的过程，宏观上能够在头脑中梳理解题思路，再现分析问题的思维过程；微观上通过线条将思维的触角延伸到解题的每一个环节，使学生的思维对每一个环节都比较清晰，便于学生面对具体问题时进行方法迁移，体会“拟定计划”之关键.

师：这三张思维导图为我们提供了思考问题的引导框架，大家能谈谈你对这三种方法的认识吗？

师：这需要我们有完整的知识结构和解题经验的积累，并能在不同的情境下对问题进行转化.

生6：解法二和解法三与解法一的运算顺序相刚好反，都是先利用线段AF1,AF2的相等关系并结合图形得出点A位置的特殊性(这里我觉得应养成把题中所求线段长及时标注在图中的习惯，有利于发现几何关系.)，从而迅速锁定点A坐标，接下来，法二利用坐标关系便捷的算出点B坐标，法三则从图形中的几何特征入手，利用三角形相似也轻松得出了点B的坐标，真是殊途同归呀！纵观整个法二和法三的求解过程，不仅运算长度大大缩短，而且较法一大大降低了运算量.我认为解法三是最简捷的解法，平几知识的介入使其运算量小，且易于操作， 真正体现了多想少算的解题理念.因此，在解决圆锥曲线问题时，我们要注重充分挖掘图形中的几何关系，结合图形的特点利用中垂线的性质、三角形相似的性质等进行逻辑推理和转化求解，直到问题解决为止.这要求我们平时要注重对直观想象和逻辑推理等能力的培养.

师：解法二和解法三的顺利进行得益于点A特殊位置的发现，同时也向我们渗透了一种解题的哲学思想—普遍性都寓于特殊性之中，发现了问题的特殊性，就找到了问题的突破口.

学生通过对第一阶段数学活动过程的反思和总结，虽然形成了较为有条理的数学活动经验，但这时经验的提升也仅限于解决一个高考题的活动经验，同时，学生由于受自身知识水平、社会阅历和解题经验等因素的制约，很难将活动经验顺利应用于新的情境中去，这时，就需要我们教师帮助学生在合作交流的过程中促进数学活动经验的内化和感悟，以便更好的实现迁移.

3.内化感悟，迁移基本活动经验

教师作为数学教学的组织者、引导者，要帮助学生将数学活动中内隐的数学思想方法转变成相对外显的、可以表达的知识和技能等数学活动经验，让学生感悟到这种经验已经脱离了某个具体的情境，显得更加直观，有一种“眼见为实”的感觉，而且在遇到新问题时可以自发的运用这些经验成功解决，让学生感觉到学习是快乐的.

师：同学们！到目前为止，大家对这道高考题的本质有了深刻的认识，解题的最高境界是从解题中学会解题，今后当我们面对一个陌生问题时，本题处理时的哪些经验值得我们借鉴呢？

生7：解析几何问题的求解不能更多的偏重于代数运算，而忽略对几何性质的挖掘.

师：很好！解决任何数学问题都应从代数和几何两个维度来思考，这是一个普遍性的原理，解析几何问题的求解也不例外，几何性质运用恰当不仅可以优化算法路径、缩短解题长度，而且还可以降低运算量，提高我们的正确率.因此，我们的解题需要数形结合意识.

生8：一个题目中如果有多个已知条件，在运算求解时必然涉及到先用哪个条件后用哪个条件的顺序问题，按照不同的顺序求解，往往能收到令人意想不到的效果.

师：生8的观察很仔细，数学运算是高中数学六大核心素养之一，也是我们每天进行的数学活动，《课程标准》明确提出要在关联的情境中设计运算程序，解决问题.这里设计运算程序就涉及运算顺序问题，如果一味的按照题设条件的出场顺序自然求解，难免会陷入困境，这就要求我们在拟定计划时要有足够的思维量，对解题中可能出现的繁简程度和运算量作出预判，并及时进行修正和优化，确保设计出最合理的运算顺序，来提高解题的速度和精准度.

因此，平时我们一定要加强自己的思维训练，积累解题经验，以便为解题时设计合理的运算顺序提供依据.

生9：解题中我们还应加强对一些常见经验的总结，比如，本题中两个线段的等量关系，可以从向量的角度来处理.这些，有助于我们碰到类似问题时，能顺利实现转化.

师：著名数学家笛卡尔曾说过：“我解决过的每一个问题都成为日后用以解决其他问题的法则.”这句话强调了解题经验积累的重要性，熟悉一些经典套路，多往典型题型上靠拢，有助于提升我们看问题的起点，跨越思维障碍，快速、准确的洞悉问题的本质，制定出可行的解题计划实现顺利求解.这就要求我们的数学解题要实现从“就题论题“到”经验积累“的跨越，因为这些经验才是我们今后解决相关问题的利器.

学生对相关解题经验的分享，旨在由此及彼，由点到面，获得解决类似数学问题的经验，这些经验的内化，不仅能更好的帮助理解基础知识，掌握基本技能得，感悟数学基本思想，而且能对基本活动经验本身产生再认和再生，有利于学生形成更高和更完整的认知结构，养成用一般观念思考问题的习惯.比如，这道高考题与生4所说的题目虽然呈现方式不一样，但如果学生积累了 “降维”的基本活动经验，三角形相似方法的出现便是基本活动经验顺利迁移的产物.

总之，作为一名数学教师，我们应在课堂教学中给学生提供充分数学活动的机会，注重积累和提升学生的数学活动经验，让学生在对话交流与深刻反思中理解数学的本质，获取理性的数学经验，并学会用数学的眼光观察世界，用数学的思维思考世界，用数学的语言表达世界，从而有效的促进数学核心素养的形成与发展.