基于矩估计赋权和改进TOPSIS法的节水灌溉模式优选

2021-01-27张忠琼徐洪峰

节水灌溉 2021年1期

张忠琼，徐洪峰

（1.安顺学院数理学院，贵州安顺561000；2.贵州师范大学经济与管理学院，贵阳361005）

0 引言

我国农业水资源分布严重不均，许多地区农业水资源十分短缺，经常因为无法及时灌溉造成农业生产的严重损失。因此，在农业生产中全面实施高效用水节水技术，对于保证农业生产的稳定发展意义重大。实施全面的农业节水，需要对原有的用水技术与模式进行变革，发展新型的节水灌溉技术和模式。由于节水灌溉技术与模式存在许多的种类，也各有其优缺点和适用条件，因此在各地的节水农业发展过程中，如何正确的选择适宜的节水技术模式就成为一个非常重要的技术问题。节水灌溉模式优选，实质上是一个多因素综合评价问题，它的影响因素是多方面的。张亮等[1]对农业高效节水灌溉模式选择问题进行了阐述、归纳、总结和展望。系统地分析了不同的节水灌溉综合评价模型的优缺点。余乾安等[2]基于ORYZA_V3 模型对赣抚平原灌区水稻节水灌溉模式开展研究。ORYZA_V3 模型不具有普适性，只是对水稻生长模拟。戚迎龙[3]改进了经典层次分析法并对西辽河流域春玉米不同灌溉模式作系统性评价。虽然在改进中加入实际监测和调研考察数据，但该方法所得结果仍不能避免主观的核心缺陷。张旭东等[4]采用二级模糊评判综合模型对节水灌溉方式进行研究。张星星等[5]引入熵权系数评价模型，对不同节水灌溉方案进行评价和优选。这两种模型均为客观评价模型，计算权重方法单一，没能很好地考虑主客观因素的影响，评价模型相对简单。通过对这些文献分析发现：当前针对节水灌溉模式优选的研究多采用单一评价方法，指标赋权较主观，且主要对某一节水灌溉模式展开研究，分析结果多以定性分析为主。单一评价方法存在顾此失彼的缺点，主观赋权或客观赋权都不能较好地反映指标权重信息；即便采取了主观赋权与客观赋权相结合的组合集成赋权，也只是对二者间进行简单的叠加与组合，组合权重并未达到最优。本文建立了矩估计法组合权重模型来计算评价指标的权重向量，该方法确定的指标权重更为合理，且能有效地调节主观权重和客观权重比例。同时对TOPSIS方法进行改进，改进后的TOPSIS评价模型有效地解决了数据波动变化大；样点与正、负理想点等距排序紊乱的现象，具有较强稳定性和客观性。

1 研究方法

本文首先建立归一化的决策矩阵，然后建立矩估计法的组合权重模型来确定评价指标的权重向量，接着对TOPSIS 方法进行改进逐步展开研究。

1.1 归一化决策矩阵的建立

假设在某一农业灌溉区域有m 种灌溉方式可供选择，每种灌溉方式包含n个优选指标，则可确定样本矩阵X =(xij)m×n（xij为第i 种灌溉方式在第j 个指标下的原始数值，i = 1,2,…,m；j = 1,2,…,n）。

因为每个指标的单位和数量级不同，所以需要对优选指标原始数值xij（i = 1,2,…,m；j = 1,2,…,n）作归一化处理。

正向型指标归一化公式为[6]：

负向型指标归一化公式为[6]：

1.2 矩估计法组合权重模型

定义1：Ws={wsj|1 ≤s ≤p,1 ≤j ≤n}为指标主观权重集合，且这里，采用p种主观赋权法确定评价指标的主观权重。

定义2：Wt={wtj|1 ≤t ≤q - p,1 ≤j ≤n}为指标客观权重集合，且这里，采用q - p 种客观赋权法确定评价指标的客观权重。

评价指标的组合权重向量记为W =(w1,w2,…,wn)T，建立下列权重向量优化模型：

式中：α和β分别为主观权重和客观权重的相对重要系数。

假设q个样本来自两个不同的总体，根据矩估计法的基本思想，首先，计算指标xj（j = 1,2,…,n）的主观权重分量wsj和客观权重分量wtj的期望值

进一步，求出指标xj（j = 1,2,…,n）的相对重要系数αj和βj

对于规一化决策矩阵中的评价指标，将它们看成为分别从两个不同总体中取出的n个样本，依据矩估计理论可得：

对于每一个指标xj（j = 1,2,…,n），当然是f(wj)越小越好，因此，模型（3）可转化为：

对模型（7）采取线性加权，得：

通过Lagrange 乘子法对式（8）求解，可确定评价指标的最优组合权重：

1.3 改进TOPSIS评价模型

TOPSIS（Technique for Order Preference by Similarity to an Ideal Solution）法是C.L.Hwang 和K.Yoon 于1981年首次提出，该方法通过构造多属性问题的理想解和负理想解，并以靠近理想解和远离负理想解两个基准作为评价各方案的依据[7]。因此，TOPSIS 法又称为双基点法。TOPSIS 方法只是单纯考虑指标之间的欧氏距离，不能反映评价指标序列的动态变化，在做决策分析时存在不足，尤其是针对动态序列进行决策。灰色关联分析能够反映各方案的内部变化规律，弥补了TOPSIS方法的不足。文中运用TOPSIS 模型结合灰色关联法对TOPSIS进行改进，定义了一个新的正、负理想点集和相对贴近度公式，同时还考虑了决策者的不同主观偏好。改进的TOPSIS 模型通过计算评价对象之间关联程度，解决数据波动变化大；在计算欧式距离时，避免出现样点与正、负理想点等距排序紊乱现象，具有较强稳定性和客观性。

把利用矩估计法确定的评价指标的组合权重向量W =(w1,w2,…,wn)T乘以归一化决策Y =(yij)m×n得到加权归一化决策矩阵：

式中：zi(j)为各种灌溉方式的zij值。

式中：i = 1,2,…,m；j = 1,2,…,n；ρ 称为分辨系数，ρ ∈[0,1]，一般取ρ = 0.5。

式中：a 和b 分别表示农业灌溉区域形状和位置的偏重程度，且a + b= 1，参数a和b的取值一般由决策者事先给定。

计算各备选灌溉方式的相对贴近度Di：

根据灌溉方式相对贴近度Di的大小进行排序和优选，Di的值越大，说明该灌溉方式的节水灌溉效益越高，反之，则越低。

2 实例应用

下面把本文构建的基于矩估计赋权和改进TOPSIS 法的优选模型应用于文献[8]中的应用实例来展开实证分析，进而确定最优的节水灌溉方式，原始指标数据见表1。

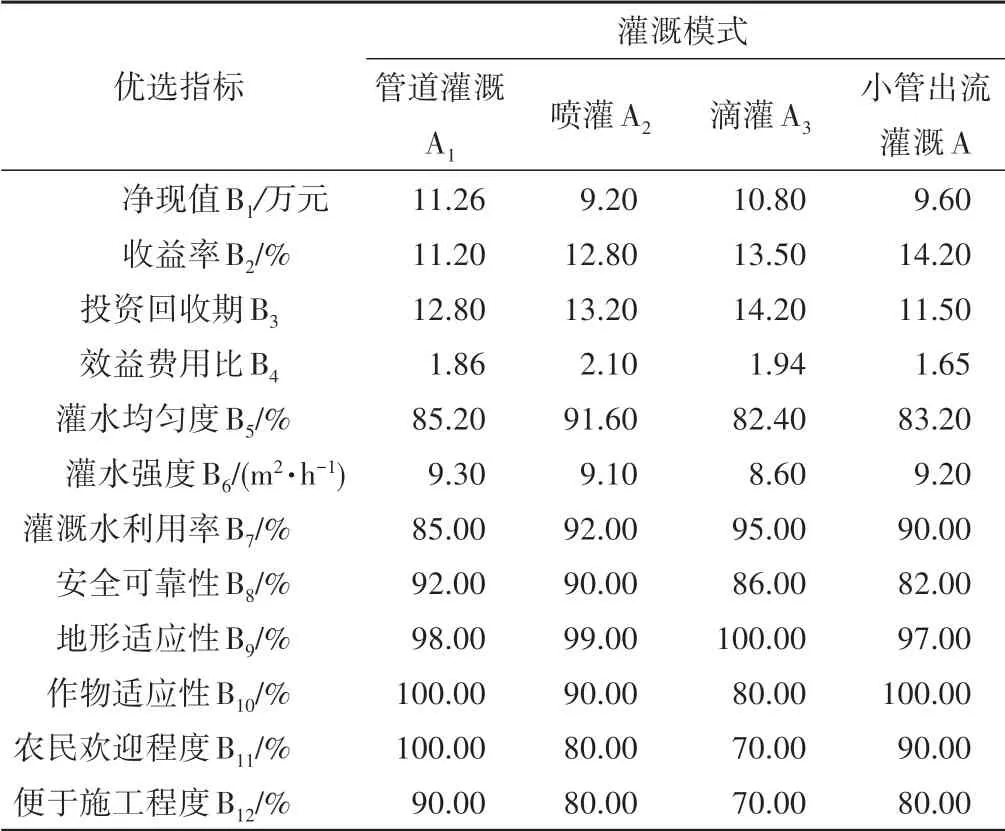
表1 各灌溉模式的优选指标值

表1 中，投资回收期为成本型指标，其余均为效益型指标。利用式（1）和（2）对表1中的各指标的原始数据值进行归一化处理，得到下列归一化决策矩阵Y：

文中分别采用G1法[9]和改进层次分析法[10]来确定指标的主观权重；采用变异系数法[11]和改进熵权法[6]来确定指标的客观权重。然后通过构建的矩估计法组合权重模型来确定优选指标的组合权重向量。

利用G1法和改进层次分析法求得的指标主观权重为：

W11=(0.094 2，0.057 1，0.132 1，0.226 8，0.068 8，0.043 2，0.063 2，0.091 8，0.047 3，0.069 0，0.059 0，0.047 9)T

W12=(0.087 9，0.042 2，0.182 7，0.379 2，0.005 9，0.017 8，0.053 3，0.104 4，0.011 6，0.060 3，0.034 7，0.020 1)T

利用变异系数法和改进熵权法求得的指标客观权重为：

W21=(0.083 5，0.083 5，0.083 3，0.083 5，0.083 0，0.082 9，0.083 0，0.083 0，0.082 8，0.083 6，0.084 4，0.083 5)T

W22=(0.100 4，0.072 0，0.081 4，0.074 4，0.131 7，0.068 6，0.073 0，0.079 2，0.082 9，0.077 7，0.083 2，0.075 6)T

把W11、W12、W21和W22代入式（4）和（5）即能确定各指标的主观权重相对重要系数αj（j = 1,2,…,12）和客观权重相对重要系数βj（j = 1,2,…,12），所求结果如下：

αj=(0.497 5，0.389 7，0.656 5，0.793 3，0.258 1，0.287 1，0.427 5，0.547 4，0.262 2，0.444 9，0.358 6，0.299 4)T

βj=(0.502 5，0.610 3，0.343 5，0.206 7，0.741 9，0.712 9，0.572 5，0.452 6，0.737 8，0.555 1，0.641 4，0.700 6)T

根据矩估计法的基本思想，将αj和βj代入式（6）就能最终确定主观权重的相对重要系数α和客观权重的相对重要系数β，经计算得到α = 0.435 2，β = 0.564 8。

分别把W11、W12、W21、W22及α、β的值代入优化模型（8），通过MATLAB 编程求解得到各评价指标的最优组合权重向量W，所求结果为：

W=(0.087 4，0.074 4，0.099 2，0.129 9，0.080 1，0.069 7，0.076 4，0.085 9，0.071 5，0.078 5，0.075 5，0.071 5)T

将上述求得的最优组合权重向量W和归一化决策矩阵Y相乘即得到加权归一化决策矩阵Z，根据式（11）和（12）确定灌溉模式的正、负理想点集，得：

利用式（13）和（14）先来确定各灌溉模式与正、负理想点集的灰色关联系数和再根据式（15）和（16）计算各灌溉模式与正、负理想点集的灰色关联度和所得结果见表2。

表2 灰色关联度

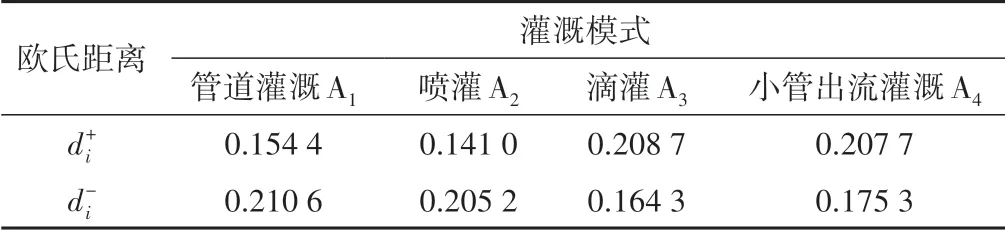
表3 欧式距离

D1= 0.5095，D2= 0.5197，D3= 0.4941，D4= 0.4888

因为D2＞D1＞D3＞D4，所以A2＞A1＞A3＞A4，喷灌这种灌溉方式的节水效益是最优的，管道灌溉方式次之，这一评价结果与在灌溉方式中多采用喷灌和管道灌溉这两种模式相吻合。

为了验证文中所提方法的合理性和有效性，现把文献[12]～[15]中的方法应用于文中的算例，对结果作对比分析，对比结果见表4。

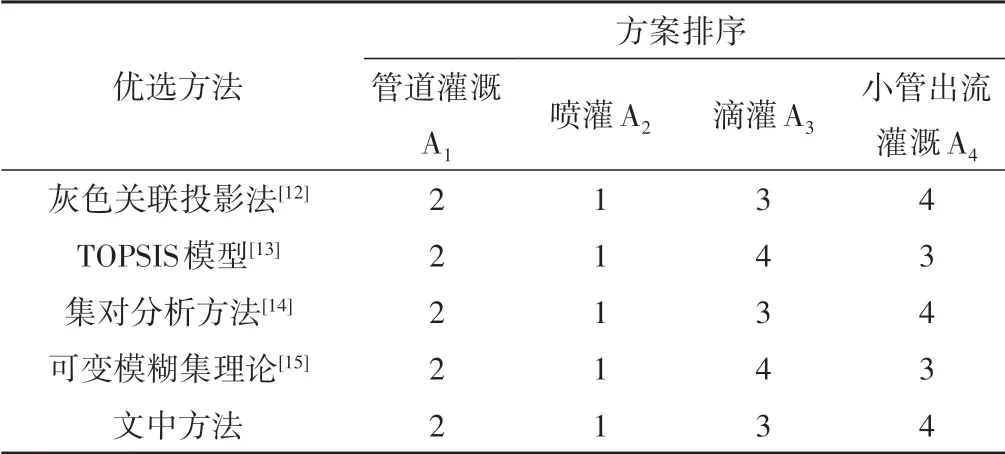
表4 5种不同方法的对比结果

从表4可以看出，文中方法与文献[12]和[14]的排序结果是一致的，与文献[13]和[15]的排序结果略有差别，但是喷灌和管道灌溉这两种灌溉模式均是排名第一和排名第二的，为优先选择的节水灌溉模式。在计算过程中还发现，采用文中方法得到的这4种灌溉模式的相对贴近度间的差异程度更小，相比利用文献[12]、[14]方法得到的4种灌溉模式的相对贴近度数值大小的差异程度则很大，因此本文方法具有较强的灵敏度。将优选指标的某一个数值做细小的改动或主观偏好系数取不同的参数时，算法的计算结果保持不变。微小的评估误差不会导致不同的评价结果，因此文中的方法具有鲁棒性，这是文献[12]～[15]中的方法不具备的。