MU-MIMO单比特ADC系统中软输出检测算法

王华华, 余永坤, 于 敏

(重庆邮电大学通信与信息工程学院, 重庆 400065)

0 引 言

为了应对所预测的无线数据业务爆炸式增长,大规模多输入多输出(multiple input multiple output, MIMO)得到了人们的关注[1]。然而,大规模MIMO系统显著地增加硬件成本和射频电路的功耗[2]。在射频链的所有部件中,模拟数字转换器(analog-to-digital converter, ADC)是最耗电的部件,其功耗随着量化比特的增多呈指数型增长[3]。为了解决功耗的问题,文献[4-6]提出在大规模MIMO系统中使用混合精度ADC,其中高精度ADC主要用于信道估计,低精度ADC主要用于接收用户信息进行用户数据的恢复。关于低精度ADC的界定,学术界定义为量化比特数为1～3 bit的ADC;而在产业界,对低精度ADC没有较明确的界定。文献[6]对采用混合精度ADC的大规模MIMO系统的性能进行分析,结果表明在相同的硬件开销下,相比于采用高精度ADC的大规模MIMO系统,该系统可以获得更高的总速率和更低的功耗。

针对单比特ADC下的信号检测,通常采用硬检测和软检测两类算法。在文献[7]中提出了最佳的最大似然检测(maximum likelihood detection, MLD)算法,并对最大似然检测器进行了改进,提出逼近最大似然检测(near-maximum likelihood detection, NML)算法。此外,文献[8-9]分别给出了基于有监督学习和编码理论的新MIMO检测框架。尽管上述算法有很好的未编码符号差错率性能,但在有信道编码系统中的误帧率(frame error rate, FER)较高。主要是由于硬判决输出大大降低了Trubo码、低密度奇偶校验码(low density parity check code, LDPC)和极化码等信道编码的性能。

文献[10]针对采用单比特ADC的上行MU-MIMO系统提出了软输出检测(soft output detection, SOD)算法,该算法在有信道编码系统中的FER比其他硬检测算法的FER更低。但是由于该算法对每个用户都会搜索整个码字空间,其计算复杂度为O(KMK)[11],其中K为用户数量,M为调制进制数。为了降低SOD算法的复杂度,文献[11]提出了单比特连续干扰消除软输出算法,该算法每计算出一个用户的软信息就用信道解码算法解出对应的比特信息,然后使用循环冗余校验(cyclic redundancy check, CRC)判断解出的信息比特是否正确,如果CRC正确,那么计算下一个用户的软信息时就将解码正确的用户信息减掉,所以计算下一个用户的软信息时其搜索空间就变成原来的一半,该算法的检测复杂度能达到O(MK)。然而该算法必须要和信道译码算法一起使用才能工作,且此算法需要将译码正确的数据再做一次信道编码流程,文献[11]中所得计算复杂度并未考虑该因素。文献[12-21]和文献[22-25]分别讨论了低精度ADC和单比特ADC下的信号检测问题。

针对现有软检测算法复杂度高的问题,本文使用串行干扰消除算法思想,结合文献[10]的检测算法提出了排序多用户单比特串行干扰消除软输出检测(ordered multi-user one-bit successive interference cancellation soft output detection, OMuOSIC-SOD)算法。

1 系统模型

文献[4-6]提出的采用混合精度ADC的大规模MIMO系统如图1所示,假设MU-MIMO系统中发送端有K个单天线终端,基站配备Nr根天线。基站配备Nh根天线用于信道估计,估计出的信道冲激响应矩阵为H∈CNr×K,由于本文重点在该系统的信号检测问题,在此不对信道冲激响应矩阵的估计算法做详细介绍,并假设基站已经通过信道估计算法得到信道矩阵H。

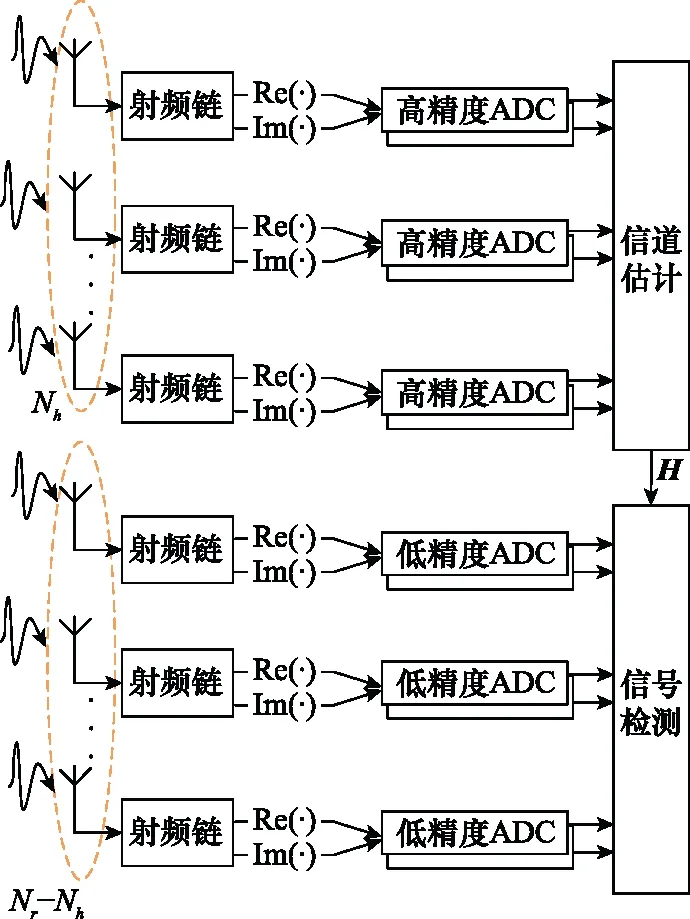
图1 采用混合精度ADC的大规模MIMO系统Fig.1 Massive MIMO system with mixed-precision ADC

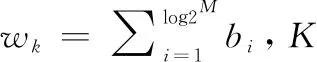
假设第k个用户调制后的数据用xk=swk∈S表示,则K个用户传输的信号向量为x=[x1,x2,…,xK]T,设M进制调制的星座集为S={s0,s1,…,sM-1},星座集信号的平均能量为E(|si|2)=1。基站接收到的未量化的复信号为

y=Hx+n∈CNr

(1)

式中,H∈CNr×K是K根发送天线与Nr根接收天线之间的信道矩阵;hi∈CNr×1表示第k根发送天线与Nr根接收天线间的信道向量;n=[n1,n2,…,nNr]T表示复高斯白噪声向量,服从零均值和方差为σ2的复高斯分布,即ni～CN(0,σ2)。

为了后续叙述方便,将复信号转化为实信号,且令N=2Nr。转化后的信号模型为

(2)

在MU-MIMO单比特ADC系统中,基站的每个射频链路配备两个单比特ADC,分别对信号的实部和虚部进行量化。假设用sign(·)表示量化函数,其量化规则如下:

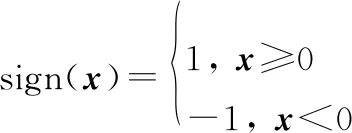
(3)

经过量化后得到的系统模型为

(4)

2 OMuOSIC-SOD算法

文献[10]已为该系统提出一种性能最好的软检测算法,但是其算法的检测复杂度太高,不宜在工程实践中使用。复杂度过高的原因在于每次检测用户的信息都是全空间搜索,没有利用已检测用户的信息,其次是没有适当舍弃检测精度来降低计算复杂度。SOD算法的复杂度过高的问题可以用串行干扰消除算法的思想解决。为此本文结合SOD算法和串行干扰消除的思想提出OMuOSIC-SOD算法。

第i次检测时,将式(1)接收信号写为

(5)

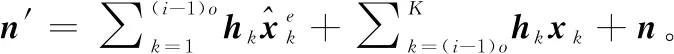
(6)

将式(6)代入SOD算法,得到的等效N路并行B-DMC如图2所示。

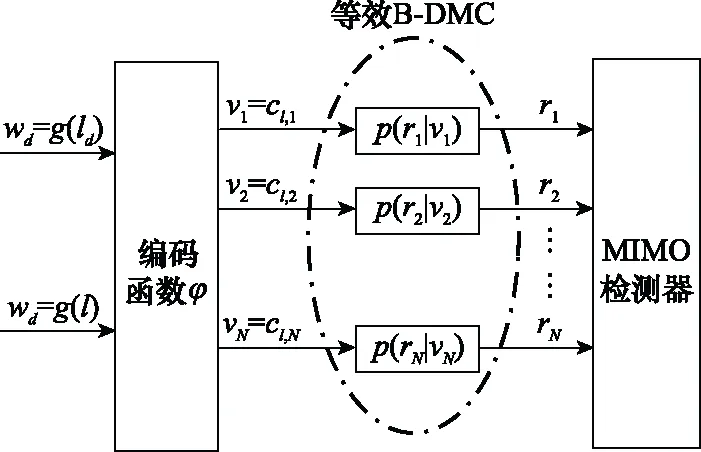
图2 等效N路并行B-DMCFig.2 Equivalent N-way parallel B-DMC

2.1 等效N路并行B-DMC

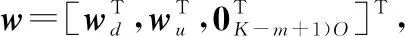
(1) 信道输入

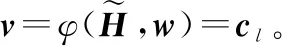
(7)

(2) 转移概率

如图2所示,等效N路并行B-DMC信道包含N个并行二进制离散无记忆信道。对于第i个子信道,转移概率为

(8)

式中,错误概率el,i为

(9)

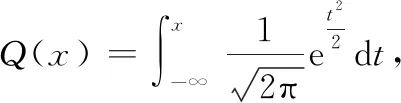
2.2 计算软信息

定义加权汉明距离为

(10)

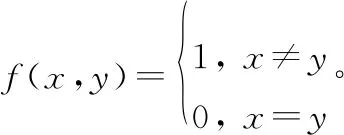
第k个用户发送信号xk与接收信号r的后验概率与转移概率的关系如下:

P(xk=sj|r)=P(wk=j|r)=

(11)

式中,wk表示向量w去掉第k个元素后得到的向量。

由于发送信号和接收信号的先验概率是已知的,所以设发送信号概率与接收信号概率之比为A=P(wk=j)/P(r),则式(11)变为

(12)

根据文献[10]的近似,第k个用户的转移概率为

(13)

假设每个用户的每个调制符号均包含p比特信息,为了方便表示,定义

(14)

那么,第k个用户的第i比特的软输出为

(15)

式中,B(i,0)表示第i比特为0的空域码字集合;B(i,1)表示第i比特为1的空域码字集合。

2.3 排序过程

以上过程没有考虑信道的影响使接收端接收到的每个用户信号功率不同所带来的问题。通过式(5)可以看出,如果本次检测的用户信号功率高,由于把未检测的用户信息当成等效噪声,那么此时的等效噪声就比较低,检测正确的概率更大,同时下一次检测正确的概率更大;如果先检测的用户信号功率低,由于把未检测的用户信息当成等效噪声,那么此时的等效噪声就会比较高,检测正确的概率更低,同时下一次检测正确的概率更小。

然而受到信道的影响,多根接收天线上接收到的同一个用户信号的功率都不相同,如果使用某一根接收天线的接收功率进行排序,就不能反映出接收端真实的接收信号功率大小。由于OMuOSIC-SOD算法在做检测时利用了所有天线接收到的信号,所以在做排序时需要对所有天线的接收功率进行综合考虑。又由于本文考虑每个终端的发送功率相同,所以接收功率排序只需要考虑信道的影响。综合上述分析,本文提出使用信道矩阵每一列所得列向量hi的二范数的排序作为检测顺序。那么,检测顺序号i与用户索引ki的对应关系为

(16)

3 计算复杂度分析

根据算法的流程可知,OMuOSIC-SOD算法的排序过程只需要进行K次求二范数运算,其计算复杂度可以忽略不计,计算复杂度主要体现在对整个星座空间的搜索上。

在实际应用中可以根据信噪比和FER要求来调整OMuOSIC-SOD算法每次检测的用户数量,以此来控制算法的计算复杂度,从而保证处理的实时性需求。

4 仿真结果及分析

为了验证所提算法在有信道编码系统中的性能,本节给出Matlab环境下的蒙特卡罗仿真结果,将所提的OMuOSIC-SOD算法与文献[10]提出的SOD算法、文献[7]提出的逼近最大似然(near maximum likelihood, NML)算法以及文献[6]提出的ZF算法在有polar编码的MU-MIMO系统中进行对比。仿真实验中使用5G协议中的polar编码,码率设置为1/2,码长设置为128 bit,译码算法统一采用串行抵消列表(successive cancellation list, SCL)算法,信道采用瑞利信道,即H通过独立同分布的均值为0,方差为1的循环对称复高斯随机变量生成,基带信号的调制方式为正交相移键控(quadrature phase shift keying, QPSK)。

图3是4×32 MIMO时的FER性能图,从图中可以看出,相同信噪比下,OMuOSIC-SOD算法比两种硬判决算法——ZF算法和NML算法的FER低很多;当FER为10-3时,相对于ZF算法和NML算法,两用户OMuOSIC-SOD算法的性能有3.2 dB左右的提升;两用户OMuOSIC-SOD算法的性能与SOD算法性能差距很小,在FER达到10-3时,两用户OMuOSIC-SOD算法与SOD算法的性能只差约0.2 dB。

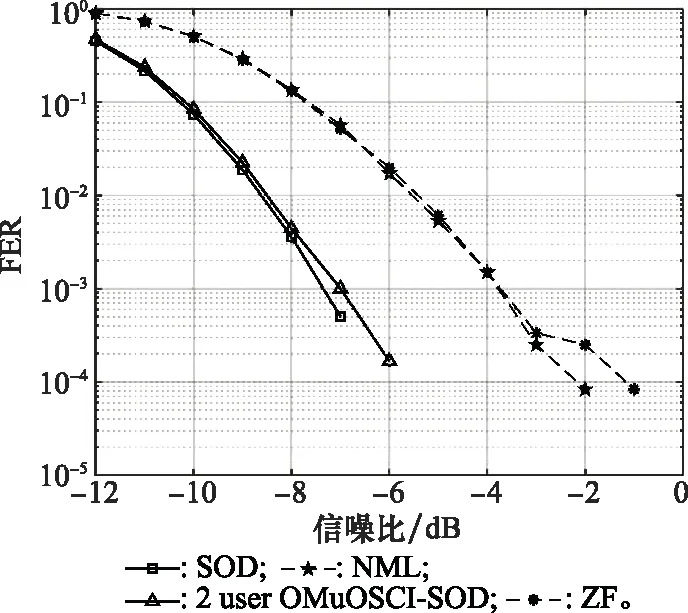
图3 4×32 MIMO下FER性能对比Fig.3 Performance comparison of FER in 4×32 MIMO

图4是8×32 MIMO下各个算法的FER性能图。图4与图3所反映的结果一致,由于发送用户增多所以每种算法的FER性能较4×32 MIMO时性能均变差。在FER达到10-3时,四用户OMuOSIC-SOD算法与SOD算法的差距大约为0.4 dB。当信噪比变高时,OMuOSIC-SOD算法的FER变化比较平缓,这是由于串行干扰消除带来的错误传递所导致的。

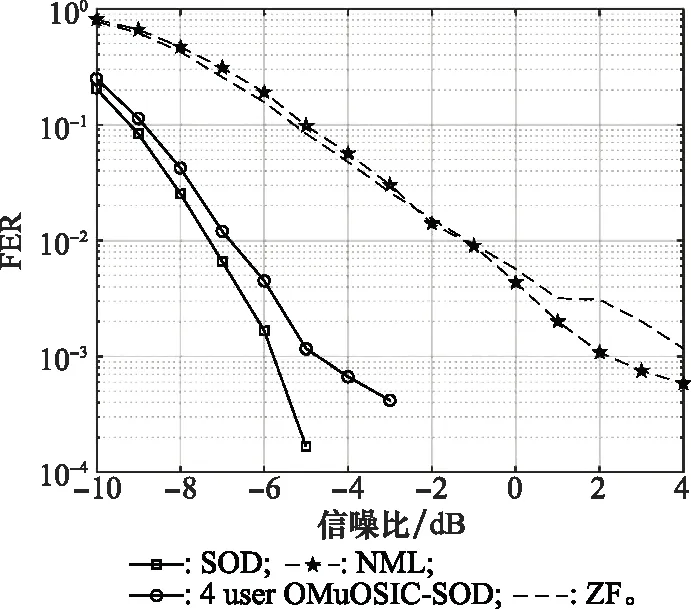
图4 8×32 MIMO下FER性能对比Fig.4 Performance comparison of FER in 8×32 MIMO

图5是4×32 MIMO下OMuOSIC-SOD算法在检测不同用户数量时的FER性能对比。从图中可以看出在相同信噪比下,每次检测的用户数量越多,OMuOSIC-SOD算法的FER越低,也就是说每次检测的用户越多其FER性能越接近SOD算法,但此时OMuOSIC-SOD算法的计算复杂度也越接近SOD算法;在FER为10-3时,两用户OMuOSIC-SOD算法、四用户OMuOSIC-SOD算法、六用户OMuOSIC-SOD算法和SOD算法的性能差距均约为0.6 dB。

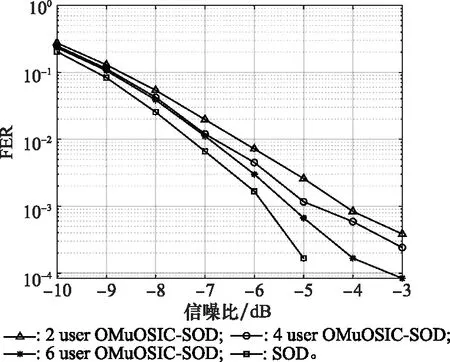
图5 8×32 MIMO下OMuOSIC-SOD算法FER性能对比Fig.5 Performance comparison of FER for OmuOSIC-SOD algorithm in 8×32 MIMO

5 结 论

配备单比特ADC的MU-MIMO系统中的软输出检测算法的检测性能很好,但是该算法的计算复杂度很高,不利于工程实现。针对现有软检测算法复杂度高的问题,利用串行干扰消除的思想和软输出检测算法提出OMuOSIC-SOD算法。OMuOSIC-SOD算法相对于SOD算法的优点在于其计算复杂度和检测精度可以动态调整。

仿真表明,OMuOSIC-SOD算法的FER均低于NML和ZF这两种硬判决算法。虽然SOD算法的检测性能比OMuOSIC-SOD算法好,但是OMuOSIC-SOD算法可以增加或减少每次检测的用户数量,使算法在检测性能和检测复杂度方面达到平衡,在实际应用时可以根据实时性要求、FER要求和信噪比来调整每次检测的用户数量。