基于自适应变异PSO-SVM的APU性能参数预测模型

王 坤, 侯树贤, 王 力

(中国民航大学电子信息与自动化学院, 天津 300300)

0 引 言

辅助动力装置(auxiliary power unit, APU)实质是一台小型涡轮发动机,是飞机重要的功能子系统,通常位于飞机的尾端。其可以只利用飞机电池启动,一旦运行,将为飞机系统提供电力,为空调和发动机启动提供电源和气源,也有少量的APU可以为飞机提供附加推力。APU使飞机不依靠地面的支持设备提供电源或气源,更具有独立性和舒适性,增大了飞机的机动性和灵活性[1]。

APU性能参数预测,是指通过一定的有效方法对表征APU各部件工作状态密切相关的各种参数进行监测,并根据监测数据分析获得各部件工作状态的变化趋势,从而对APU性能做出准确的判断,以保障飞行安全,提高APU维修的经济效益。APU性能参数数据本质上是一个时间序列。因此,对APU性能参数预测就是对时间序列的预测。时间序列又称动态数列,是指将某种变量的一组观察值,按时间先后顺序排列而成的数列。时间间隔可以是天、周、月、季、年等。

时间序列预测法是通过分析时间序列所反映出来的发展过程、方向和趋势,进行类推或延伸,借以预测下一段时间趋势变化或可能达到的水平。FLORES等[2]将神经网络用于时间序列预测。王辉等[3]利用权重思想拟合指数平滑和混沌预测方法,对飞机APU的排气温度(exhaust gas temperature, EGT)进行预测。董平[4]使用比例危险模型来预测APU剩余寿命。宋云雪等[5]建立混沌预测算法,对EGT进行预测。杜维仲等[6]建立基于长短期记忆(long short-term memory, LSTM)网络的APU启动阶段参数辨识模型。皮骏等[7]采用改进的果蝇算法优化广义回归神经网络(general regression neural network, GRNN),并用优化后的GRNN对航空发动机EGT进行预测。丁刚等[8]提出了一种基于过程神经网络的航空发动机EGT预测方法。YILMAZ[9]利用EGT与发动机其他性能参数之间的关系对EGT进行了评估。陈钦贵等[10]将径向基过程神经网络的数据挖掘算法应用到实际的航空发动机EGT的预测。张一震等[11]将改进后的集成学习算法用于航空发动机气路参数预测。刘小鱼[12]利用随机森林、支持向量机(support vector machine, SVM)、核极限学习机进行航空发动机气路参数预测。唐敏杰[13]通过APU的性能状态运行参数,采用统计分析的方法建立APU的监控模型。KUMAR等[14]将自回归和移动平均技术用于航空发动机EGT预测。戴邵武等[15]提出改进经验模态分解与支持向量回归结合的方法来预测航空发动机EGT。李艳军等[16]提出采用模糊信息粒化和优化的SVM来预测航空发动机参数的变化趋势。NIETO等[17]采用混合粒子群优化(particle swarm optimization, PSO)-SVM的模型预测飞机发动机的剩余使用寿命。于广滨等[18]建立基于支持过程向量机的航空发动机EGT预测模型,并利用遗传算法(genetic algorithms, GA)对模型参数的选择进行优化。皮骏等[19]建立改进量子PSO算法优化支持向量回归机的航空发动机EGT预测模型。ZHAN等[20]提出混合PSO-SVM模型,用来预测飞机轮胎与涂层之间的摩擦系数。曹惠玲等[21]采用基于滑动时窗策略的SVM对航空发动机性能参数进行预测。蔡坤烨等[22]建立基于SVM的APU故障预测模型。ZHANG等[23]将SVM方法和神经网络算法应用到飞机整体结构损伤的评估系统中,结果表明SVM优于神经网络算法。

目前,SVM理论已广泛应用于时间序列预测领域,并成为线性和非线性回归问题的一种解决方案。与传统的预测方法相比,其在预测结果的精确性和一致性上具有明显的优势。SVM克服了神经网络的固有缺点,例如局部最小化、过度学习和架构选择以及过分依赖经验的问题。但是在实际应用中,SVM复杂度受模型中惩罚参数和核参数的影响,这些参数是由经验和反复实验确定的,具有很大的随机性,降低了模型的预测效果。要构建一个性能良好的SVM模型,关键在于选择核函数。核函数的选择包括两部分:一个是选择核函数类型,另一个是选择核函数相关参数。如何基于具体数据选择合适的核函数是SVM应用领域的主要问题,目前仍然没有特定的理论来指导核函数的选择。因此,本文采用线性递减惯性权重调整的方法,引入变异算子,提出一种基于自适应变异的PSO算法优化SVM的预测模型,并将其应用于APU关键性能参数的预测。首先,从飞机快速数据存取记录器(quick access recorder, QAR)系统收集的APU参数数据中选取特征数据, 通过偏相关理论分析选取表征APU性能的关键参数,并以此构建模型所需的训练集和测试集;然后,采用自适应变异PSO算法对SVM参数进行寻优;最后,使用优化后的SVM模型,选择不同预测步长对测试集进行预测。

1 SVM

SVM[24]由CORTES和VAPNIK首先提出,是基于统计学理论的原理性方法,可用于线性和非线性回归问题。其基本思想是通过一个非线性变换将输入空间对应于一个特征空间,使得在输入空间中的决策超曲面模型对应于特征空间中的决策超平面模型。超平面的表达式为

f(x)=ωβ(x)+b

(1)

式中,ω为权重向量,决定了超平面的方向;β(x)为非线性函数；b为阈值常数,决定了超平面与原点之间的距离。

通过引入拉格朗日乘子和满足摩西(Mercer)条件[25]的核函数,依据卡罗需-库恩-塔克条件[26]得到最终的决策函数为

(2)

式中,N为训练集的个数;αi为拉格朗日乘子；β(xi)和yi分别为训练集或测试集的输入和输出;K(x,xi)为核函数。

常用核函数的种类主要有:

(1) 线性核函数:

K(x,xi)=xTxi

(3)

(2) 多项式核函数:

K(x,xi)=(γxTxi+r)p,γ>0；r≥0

(4)

(3) 高斯径向基核函数(radial basis function, RBF):

K(x,xi)=tanh(γxTxi+r),γ>0；r<0

(5)

(4) Sigmoid核函数:

K(x,xi)=tanh(γxTxi+r),γ>0；r<0

(6)

在选择核函数来解决实际问题时,通常采用以下方法:① 利用专家的先验知识预先选择核函数; ② 在选择核函数时尝试不同的核函数,选择误差最小的核函数为最佳核函数；③ 采用SMITS和JORDAAN[27]提出的混合核函数方法。该方法并没有解决核函数的选择问题,只是将问题等价转换为权重参数的选择,同时该方法还需要分别对两个核函数确定参数,大大增加了算法的复杂程度,限制了SVM泛化能力[28]。因此,本文采用方法②,针对线性核、多项式核、高斯RBF核、Sigmoid核,通过没有优化的SVM对APU关键参数EGT和滑油温度(oil temperrature, OT)进行预测实验,其中这两个关键参数由下文中偏相关理论分析得到,对比分析在相同数据条件下的相对误差。在此过程中,控制除内核功能以外的所有参数和设置。不同核函数的SVM对EGT和OT预测误差如图1和图2所示。

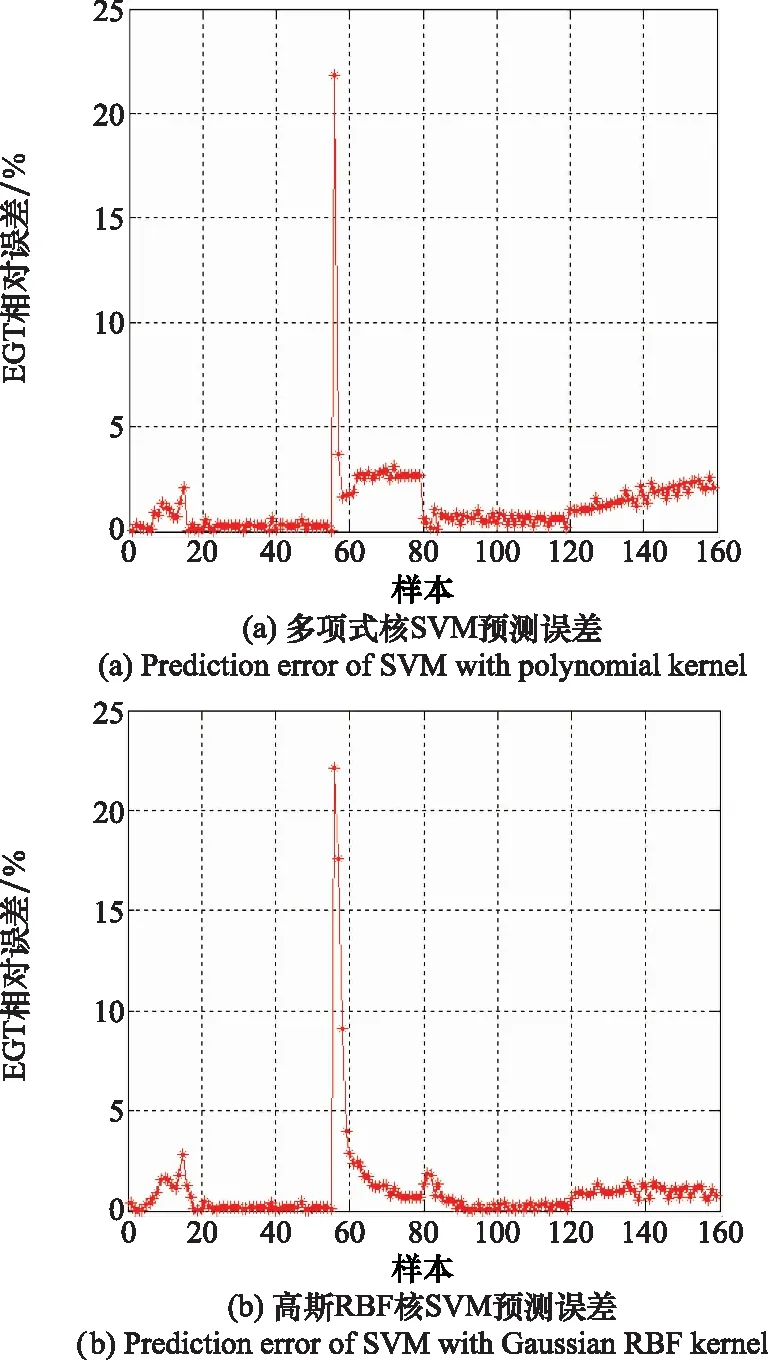
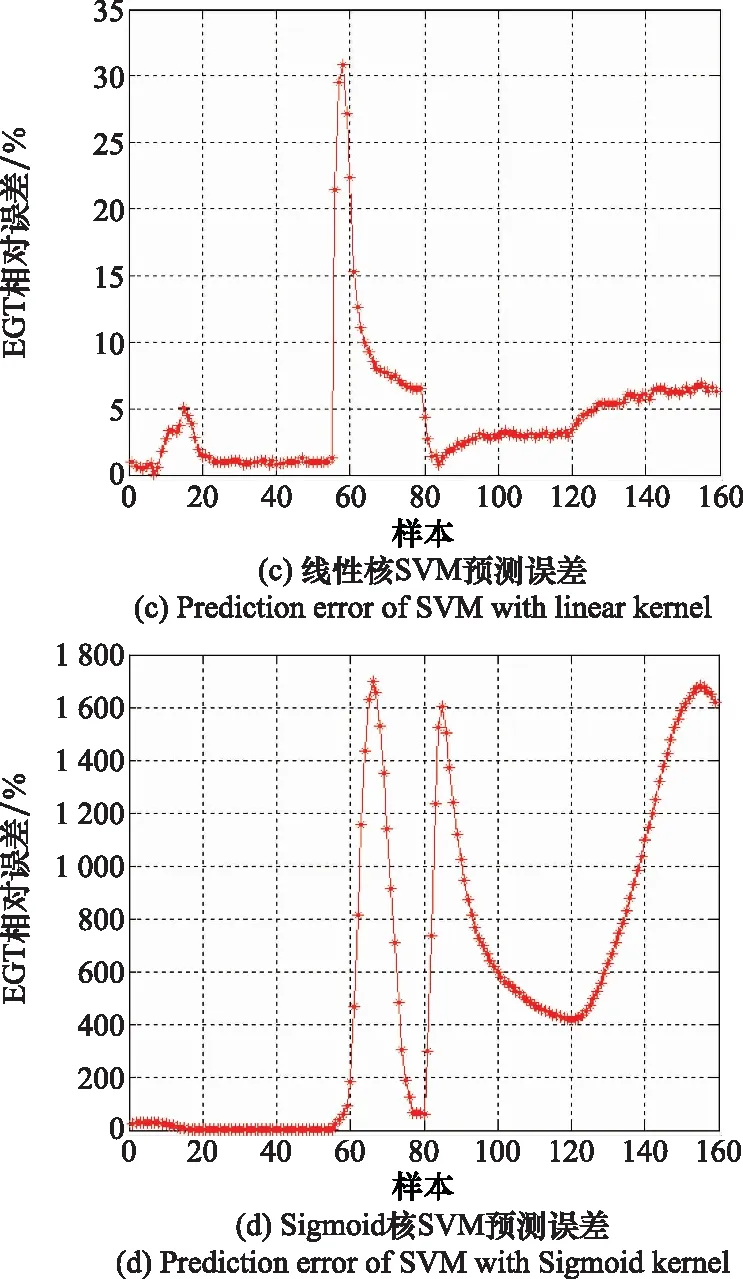
图1 不同核函数EGT误差对比图Fig.1 EGT error comparison diagram of different kernel functions

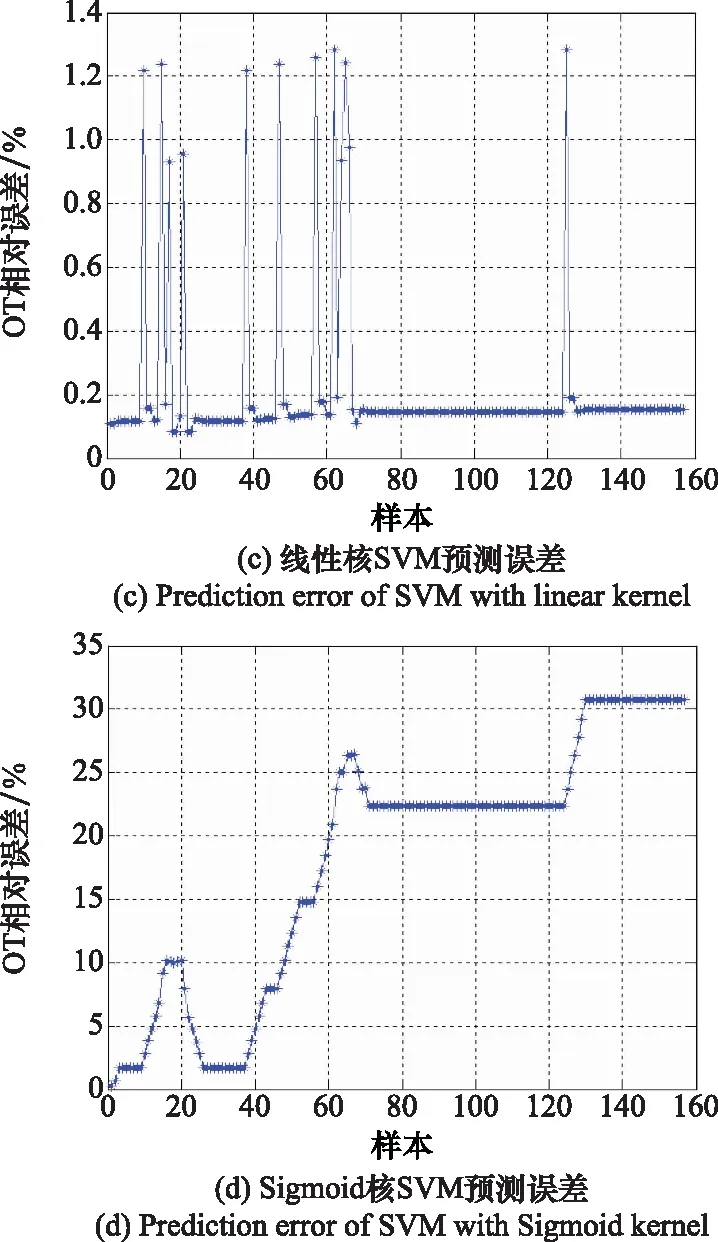
图2 不同核函数OT误差对比图Fig.2 OT error comparison diagram of different kernel functions

图1分别表示了多项式核、高斯RBF核、线性核、Sigmoid核的SVM预测EGT的相对误差。由图1可以看出,多项式核比线性核预测误差略低,Sigmoid核的误差出现大幅度波动。高斯RBF核的预测误差明显小于Sigmoid核,并且比多项式核和线性核的预测误差都低。因此,本文采用高斯RBF核作为SVM预测EGT的核函数。

图2分别表示了多项式核、高斯RBF核、线性核、Sigmoid核的SVM预测OT的相对误差。由图2可知,Sigmoid核的预测误差有上升的趋势。高斯RBF核的预测误差明显小于Sigmoid核,并且比多项式核和线性核的预测误差略低。所以,本文采用高斯RBF核作为SVM预测OT的核函数。

γ是选择高斯RBF核作为核函数之后的函数自带参数,其决定了映射到新特征空间后数据的分布,γ值越大,支持向量越少,γ值越小,支持向量越多。支持向量的个数影响模型训练与预测的速度。

另一个非常重要的参数是惩罚参数C,即对误差的宽容程度。C越高,说明越不能容忍出现误差,容易出现过拟合；反之,容易出现欠拟合。无论C过大或过小,都会导致模型的泛化能力变差。PSO算法作为一种群智能算法,其简单易行、设置参数少。用PSO算法来优化SVM参数C和γ可以较好地克服SVM存在的参数选择的敏感问题。

2 PSO算法

2.1 标准PSO算法

PSO算法[29]是通过模拟鸟群觅食过程中的迁徙和群聚行为而提出的一种全局随机并行搜索算法。在PSO算法中,每个个体也被称为一个粒子,其位置代表搜索空间中优化问题的候选解，解的适应度值由待优化问题的适应度函数决定。粒子的速度决定了其飞行的方向和距离,其运动受到两个极值的影响，一个是粒子发现的个体极值(pid),另一个是整个种群发现的全局极值(gid),粒子的速度和位置服从公式:

(7)

xid(k+1)=xid(k)+vid(k+1),d=1,2,…,N

(8)

式中,k为当前迭代次数;ω为惯性权重系数,描述粒子上一代速度对当前代速度的影响;c1和c2为非负常数,称为学习因子;r1和r2是[0,1]范围内的随机常数。为防止粒子盲目搜索,一般将其位置和速度限制在[-xmax,xmax]和[-vmax,vmax]。

为确保算法在早期有较好的全局搜索能力以获得适当的搜索速度,而在后期有较大的局部搜索速度以提高收敛精度，所以ω不宜为一个固定的常数。因此,本文采用SHI[30]提出的线性递减惯性权重,即

ω(k)=ωmax-(ωmax-ωmin)k/kmax

(9)

式中,ωmax为初始惯性权重值;ωmin为迭代到最大次数时的惯性权重值;kmax为最大迭代次数。

2.2 自适应变异PSO算法

PSO算法收敛速度快,具有很强的通用性,但同时存在着容易早熟收敛的问题。针对这一问题,应该提供一种机制,允许算法跳出局部最优,在发生过早收敛时进入解空间的其他区域以继续搜索,直到最后找到全局最优解。借鉴HOLLAND[31]的变异思想,在标准PSO算法中引入变异操作,即粒子每次更新之后,以一定的概率p重新初始化。实现步骤如下:经过k次迭代,第i个粒子在N维搜索空间中的位置为xid(k)。变异阈值q用作变异条件,当粒子满足变异条件时,将跳离当前位置,否则保持不变。变异规则采用增加随机扰动的方法,对xid(k)进行变异操作,可表示为

(10)

(11)

式中,q为0到1之间的常数;ceil(x)为将x四舍五入为大于或等于x的最接近的整数;popcmax和popcmin分别为SVM惩罚参数变化的最大值和最小值;popgmax为SVM核函数变化的最大值;r3和r4为在(0, 1)均匀分布的随机数。

变异操作可以扩大粒子搜索空间,从而使粒子可以跳出先前搜索的最佳位置并在更大的空间中搜索,同时可以保持种群的多样性并提高算法寻优的可能性。自适应变异PSO算法的流程图如图3所示。

图3 自适应变异PSO算法流程图Fig.3 Flow chart of adaptive variation PSO algorithm

3 基于自适应变异PSO-SVM预测模型

SVM预测精度与惩罚参数C和核参数γ有很大的关系。为获得具有较高预测性能的SVM,采用自适应变异PSO算法寻找SVM的最优参数组合,不仅能发挥SVM的逼近能力,而且能够提高SVM的泛化能力,最终得到自适应变异PSO-SVM预测模型。利用该模型进行APU性能参数预测的具体步骤如下。

步骤 1对表征APU性能的输入、输出参数数据进行归一化和标准化预处理,划分样本集,分为训练集和测试集。

步骤 2初始化自适应变异PSO参数,随机生成一组粒子的初始位置和速度,并设置SVM参数的初值范围。

步骤 3建立初始SVM预测模型,以均方误差(mean square error, MSE)作为适应度函数计算每个粒子的适应度值。

(12)

式中，M表示模型训练样本数量；Fi表示模型的实际训练输出值；Yi表示模型的期望训练输出值。

步骤 4将每个粒子的最优解pid设置为粒子的当前位置,并计算每个粒子的适应度值。其中，最大适应度值的单个粒子最优解是当前种群的最优解gid。

步骤 5根据式(7)和式(8)更新粒子的速度和位置。

步骤 6根据第2.2节所提变异规则执行粒子变异。

步骤 7将每个粒子的适应度值与pid进行比较,并保留更好的pid。

步骤 8将每个粒子的适应度值与gid进行比较,并保留更好的gid。

步骤 9如果满足条件,则输出最优参数C和γ,否则转到步骤4。

步骤 10将自适应变异PSO算法优化得到的最优参数代入SVM模型进行预测,反归一化输出最终预测结果。自适应变异PSO-SVM模型预测流程图如图4所示。该预测模型用于预测APU不同的性能参数,并通过比较各参数的变化趋势和APU原理来预测APU的潜在故障,并采取相应的预防措施,可为未来APU潜在异常状态的预测提供预警依据,防止APU故障的发生。

图4 自适应变异PSO-SVM模型预测流程图Fig.4 Prediction flow chart of adaptive variation PSO-SVM model

4 实验分析

实验对象选取某型APU进行研究,性能参数历史数据包括引气压力(bleed air pressure, BAP)、转速(rotate speed, RS)、发电机负载(generator load, GL)、引气流量(bleed air flow, BAF)、EGT、OT共6个参数，建立自适应变异PSO-LSTM预测模型并与小波神经网络、GRNN、Elman神经网络、标准PSO-SVM、SVM、最小二乘SVM(least squares SVM, LSSVM)、基本PSO-SVM、反向传播(back propagation, BP)神经网络模型进行对比实验。

4.1 APU性能参数选择

以某型飞机的飞行周期为例,利用飞机QAR系统提供的数据,按照时间间隔为1 min的标准来选取包含评估APU性能所需的参数数据,这些数据记录在APU启动时,并在飞机双发启动完成时结束。在此期间,APU的输出功率最高且相对稳定。以GL和BAF为输出参数,消除海拔和温度的影响,使用统计产品与服务解决方案(statistical product and service solutions, SPSS)软件对相关数据进行统计学偏相关理论分析,所得结果如表1所示。自由度(degrees of freedom, DF)表示计算某一参数时,取值不受限制的变量个数。表征相关程度的偏相关系数图如图5所示。

表1 APU性能参数偏相关分析结果

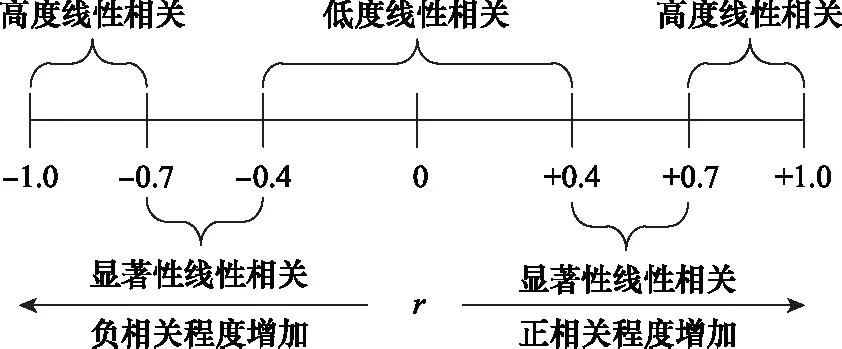
图5 偏相关系数图Fig.5 Partial correlation coefficient diagram

根据图5偏相关系数图,由表1中偏相关分析结果,可以看出BAP,RS与GL,BAF之间的相关程度较弱,但是OT,EGT与BAF,GL之间为显著性线性相关,最终确定EGT和OT为APU性能监控的关键参数。

4.2 数据预处理

由于原始数据存在一系列问题,使用这些数据所获得的预测结果通常是不准确的,所以需要对性能参数数据进行处理和标准化。通过填充丢失的数据,消除异常数据,消除噪声数据以及纠正不一致的数据来消除错误和冗余。为了提升模型的收敛速度和精度,采用min-max标准化也叫离差标准化方法,对原始数据进行线性变换使结果映射到[0,1],映射函数为

(13)

式中,xmax和xmin分别为原始数据的最大值和最小值。

4.3 自适应变异PSO-SVM模型参数设置

本文算法基于Matlab实现,通过多次重复实验确定采用自适应变异PSO算法时,设定种群数量为10,最大迭代数量为50,粒子向量维数为2,学习因子c1和c2为1.5,变异阈值q为0.8。一般而言,当ω值为0.9或0.4时,该算法具有最佳性能。这样,随着迭代次数的增加,ω值从0.9线性减小至0.4。迭代开始时较大的ω值使算法能够保持强大的全局搜索能力,而迭代结束时较小的ω值则有利于算法进行更精确的局部搜索。根据经验,惩罚参数C和核参数γ的取值范围为[0.001,10],粒子位置x的取值范围为[-6,6],速度v的取值范围为[-10,10]。

4.4 模型评价指标选择

本文选择平均绝对误差(mean absolute error, MAE)、MSE、平均绝对百分比误差(mean absolute percentage error, MAPE)、均方根误差(root MSE, RMSE)作为不同模型预测效果的定量评价指标,数值越小,说明模型预测精度和准确度越高。MAE,MAPE和RMSE的表达式分别为

(14)

(15)

(16)

式中,D表示不同模型预测样本数量;fi表示不同预测模型的实际输出值;zi表示不同预测模型的期望输出值。

4.5 预测结果分析

4.5.1 EGT预测

选取EGT数据集共计640组,其中前75%作为训练数据,后25%作为预测数据。对EGT进行单步预测,采用自适应变异PSO算法优化SVM得到最优惩罚参数C=7.028 4,核参数γ=1.151 3。不同模型对EGT的预测结果如图6所示。

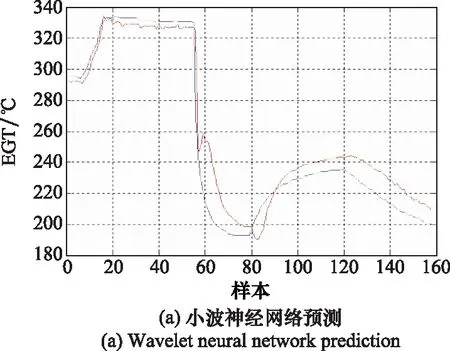
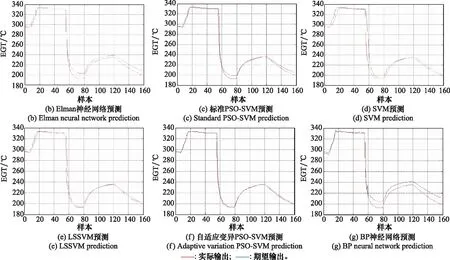
图6 不同模型EGT预测结果比较Fig.6 Comparison of EGT prediction results among different models

图6分别表示小波神经网络，Elman神经网络，标准PSO-SVM，SVM，LSSVM，自适应变异PSO-SVM和BP神经网络预测结果。结果表明,所有模型的期望输出曲线非常符合EGT实际输出值的变化趋势。但是在每个样本点处的实际输出值和期望输出值之间总存在一定的误差。本文提出的自适应变异PSO-SVM模型的预测曲线更接近EGT期望输出曲线。表2给出了不同模型对EGT预测的误差结果。

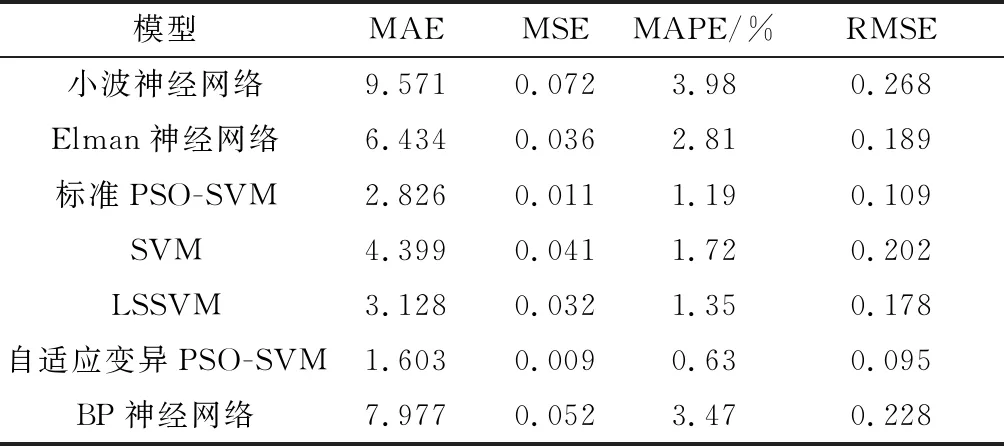
表2 不同模型EGT预测误差比较

通过比较表2中相关数据可以看出,本文提出的自适应变异PSO-SVM模型相较于其他模型在MAE，MSE，MAPE和RMSE上值都较小,取得了良好的预测效果。特别地,自适应变异PSO-SVM模型的MAPE比标准PSO-SVM模型低47%。

为了验证所提预测模型的性能,分别进行不同预测步长的误差分析,同样运用MAE，MSE，MAPE和RMSE评价指标,如图7所示。

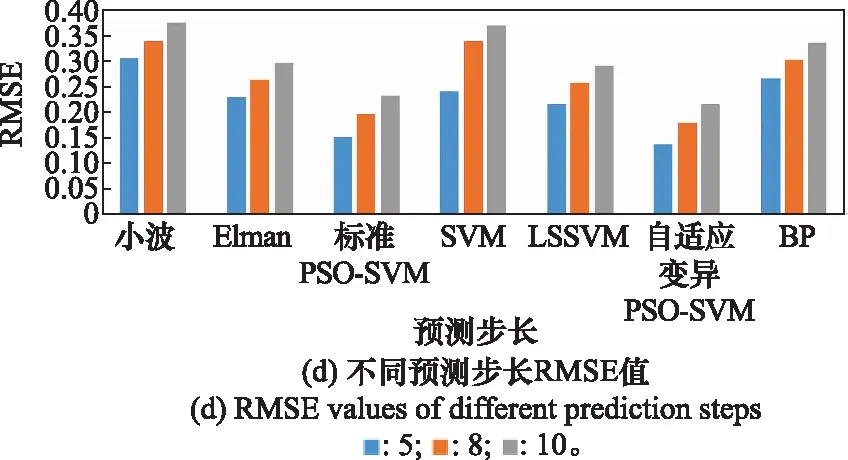
图7 不同预测步长的EGT误差分析Fig.7 Error analysis of different prediction steps for EGT

图7为不同预测步长的4种误差分析图。由图7可知,随着预测步长的增加,各预测模型的4种评价指标值均在增加,但步长在5步之内,自适应变异PSO-SVM的4个预测效果评价指标值虽然在增加,但增量不大,保持了较好的预测精度;步长在5步以上对比单步预测方式,所提模型的预测结果误差远小于其他预测模型。

4.5.2 OT预测

选取640组OT数据,其中前75%作为训练数据,后25%作为预测数据。以单步预测方式,采用自适应变异PSO算法优化SVM得到最优惩罚参数C=4.652 4,核参数γ=0.003。不同模型对OT的预测结果如图8所示。

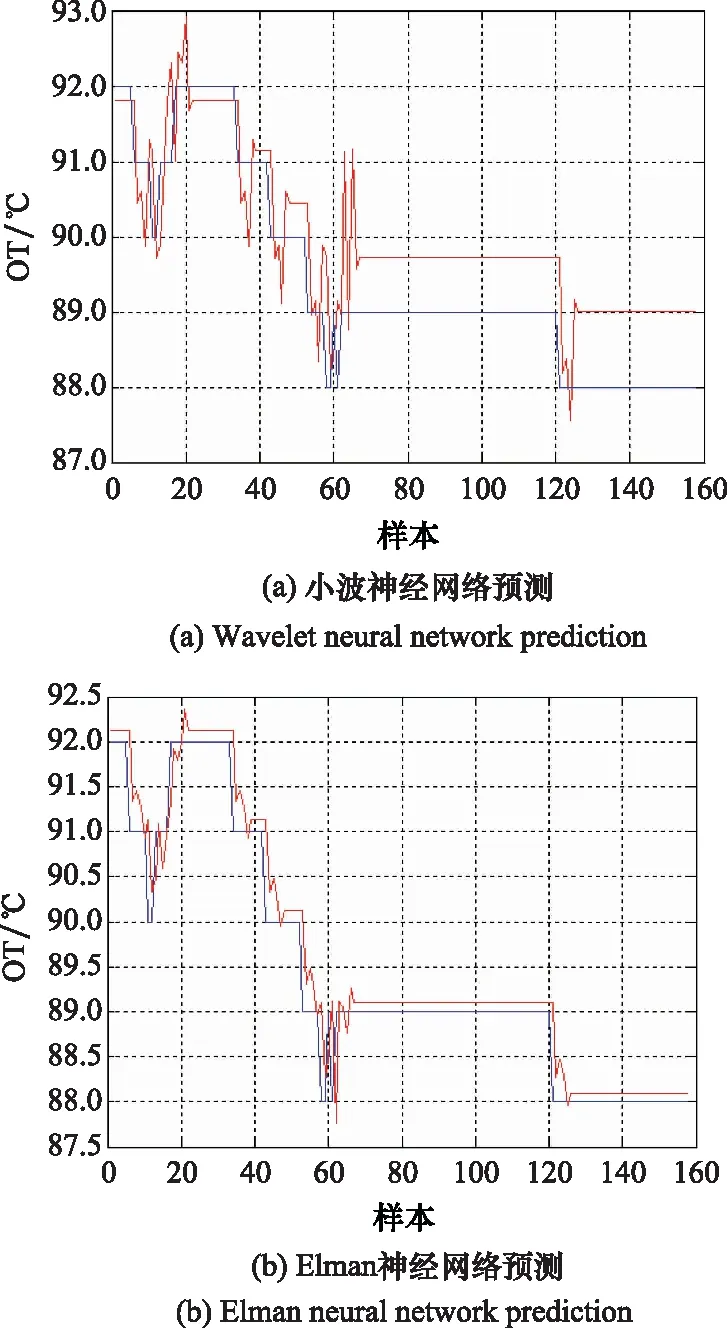
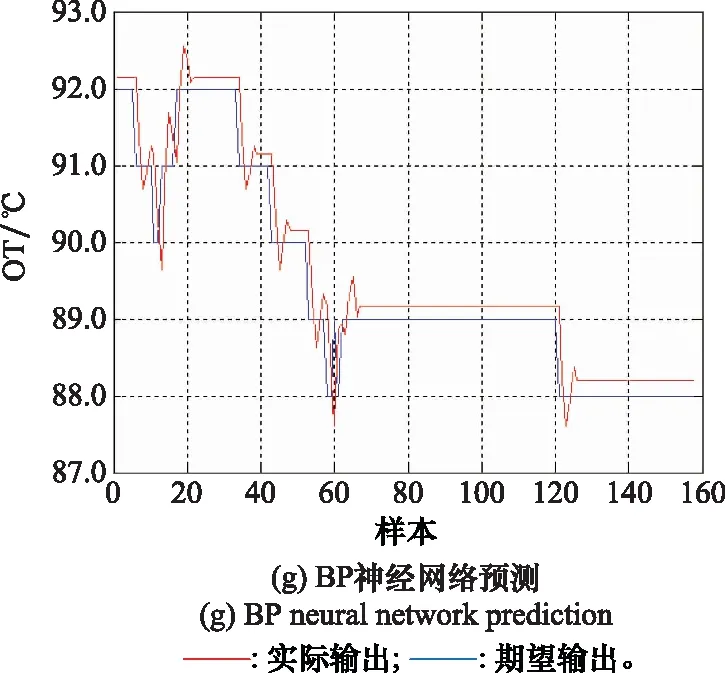
图8 不同模型OT预测结果比较Fig.8 Comparison of OT prediction results among different models

从图8中可以看到,虽然Elman神经网络预测曲线在OT值剧烈变化时刻出现小的尖峰,但其预测效果优于SVM模型与BP神经网络模型。小波神经网络预测效果最差,实际输出值与期望输出值之间有明显的误差。自适应变异PSO-SVM模型的实际OT预测曲线与期望OT曲线基本吻合,说明该模型可以准确地预测APU关键性能参数变化的趋势。为了更客观地反映所提模型的预测性能,表3给出了不同模型对OT预测的误差结果。

通过比较表3中相关数据可以看出,自适应变异PSO-SVM模型各项评价指标均优于其他模型,取得了良好的预测效果。特别地,自适应变异PSO-SVM模型的MAPE比标准PSO-SVM低29%。综合不同预测模型对EGT和OT的预测结果表明,自适应变异PSO-SVM模型对于APU关键性能参数数据的预测具有较高的预测精度。

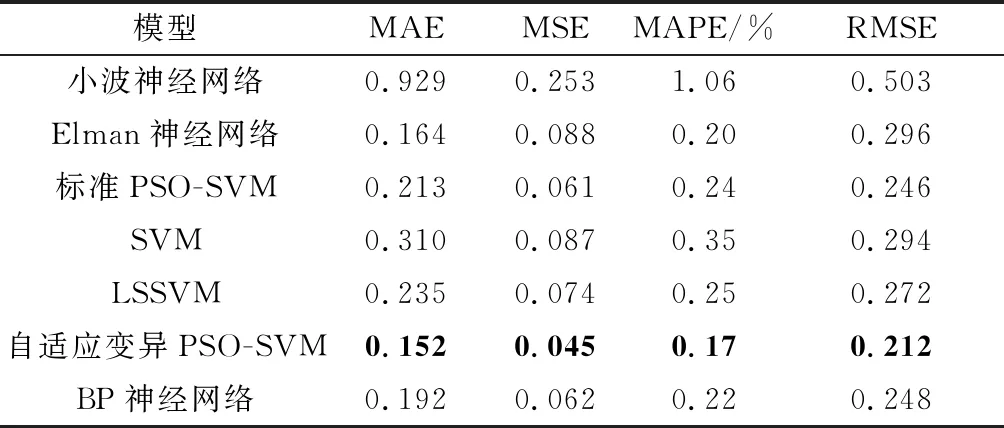
表3 不同模型OT预测误差比较

以上实验说明了OT的单步预测结果,预测结果与跟踪趋势吻合性较好。采用多步预测方式进行实验,得到不同预测步长的误差值,如图9所示。图9中不同预测步长的误差值表明:自适应变异PSO-SVM模型的4种OT误差指标均优于其他预测模型，且在不同预测步长下误差增长速度最慢。综合来说,在短期预测中,自适应变异PSO-SVM预测模型能保持良好的预测精度。此外,通过预测APU性能参数,以查看其是否在正常范围内,并结合其他的性能参数来确定将来某个时刻APU是否会处于异常状态进行故障排除,这样可以及时消除发生潜在故障的机会,避免发生重大故障。

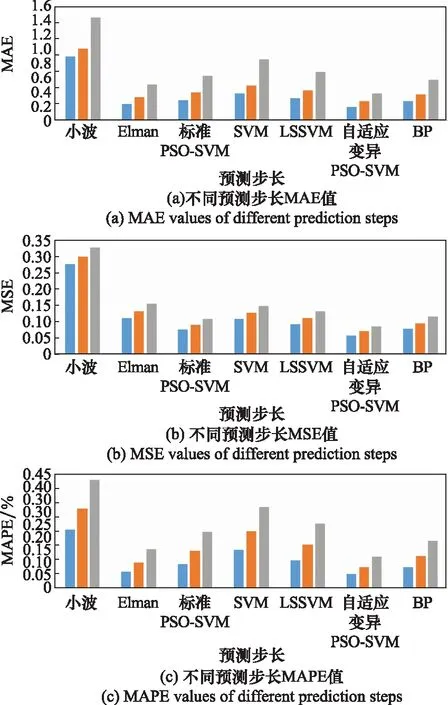
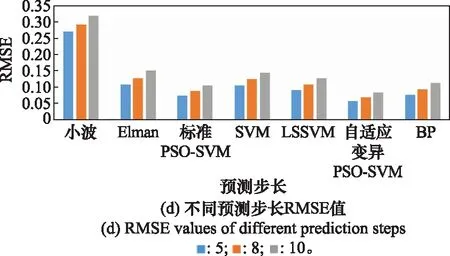
图9 不同预测步长的OT误差分析Fig.9 Error analysis of different prediction steps for OT

5 结 论

本文通过偏相关理论,分析某型APU性能参数数据,得到表征APU性能状态的关键参数,提出了一种自适应变异PSO-SVM的APU性能参数预测模型,利用关键参数数据对APU性能变化趋势进行了研究。实验采用单步和多步预测方式,分析对比了小波神经网络、Elman神经网络、标准PSO-SVM、SVM、LSSVM、自适应变异PSO-SVM、BP神经网络多种模型的预测结果和模型评价指标。实验结果表明,对于EGT的预测,自适应变异PSO-SVM模型的MAPE比标准PSO-SVM模型低47%;对于OT的预测,自适应变异PSO-SVM模型的MAPE比标准PSO-SVM低29%,可以为短期APU性能变化趋势预测提供一定的参考。