基于深度随机博弈的近距空战机动决策

马 文, 李 辉,, 王 壮, 黄志勇, 吴昭欣, 陈希亮

(1. 四川大学计算机学院, 四川 成都 610065; 2. 四川大学视觉合成图形图像技术国家级重点实验室, 四川 成都 610065; 3.陆军工程大学指挥控制工程学院, 江苏 南京 210007)

0 引 言

自1991年海湾战争开创了空中力量为主赢得战争胜利的历史,空中力量在现代战争中起着越来越重要的作用,制空权的争夺很大程度上决定了战争的胜负[1]。然而空中作战形势瞬息万变,需要采集的信息极为复杂,使得作战方在感知空战态势后做出决策变得困难,传统方法无法实现快速准确的空战策略[2]。因此,如何根据双方作战态势选取有利且精确有效的空战机动策略是空中作战的重要研究方向。

国内外学者进行了相关研究,并提出了很多空战策略生成方法,传统方法包括:影响图[3]、专家系统法[4]、微分对策法[5]、矩阵对策法[6]等。这些方法在一定程度上为空战决策提供了有效的解决方案,但也有较大的局限。如遗传算法的机动决策具有一定主观性;专家系统法的可适应性较差;微分对策法计算量过大,求解困难;矩阵对策法存在难以确保实时性等。

近年来,空战决策的研究也日益增多,文献[7]引入博弈论的思想,提出了构建自由空战指挥引导对策模型的思路,但并未给出仿真结果。文献[8]提出了一种结合近似动态规划与零和博弈的在线积分策略迭代算法,解决了机动决策建模存在的“维数灾难”问题,但有学习周期偏长、难以应付复杂机动等缺点。文献[9]利用多状态转移马尔可夫网络构建机动决策网络,满足了空战决策的实时性要求,但未利用网络参数进行学习。文献[10]提出一种进化式的专家系统树方法来研究空战决策,解决了传统专家系统方法无法应付非预期情况的问题,但其设定的仿真环境较为简单。文献[11]提出了一种矩阵对策法与遗传算法相结合的空战决策算法,建立了无人机空战决策模型,满足空战合理性与实时性需求,但只对直线和S型飞行两种蓝色战机模型进行了仿真研究。

随着人工智能的发展,出现了越来越多人工智能在博弈中战胜人类的事例:2016年人工智能Alpha飞行员打败了一位美国空军上校[12]。2018年,AlphaGo Zero在3天内自学了3种棋类游戏,轻而易举战胜了最优秀的人类棋手[13]。这些事例表现出了人工智能在智能决策方面的极大潜能。以最著名的AlphaGo为例,其主要运用了深度强化学习方法。深度强化学习将深度学习的感知能力和强化学习的决策能力相结合,是一种更接近人类思维方式的人工智能方法[14]。深度强化学习适合解决连续决策问题,而空战博弈正属于此类问题[15],因此从深度强化学习入手研究空战策略方法是一种可行思路。

本文将深度强化学习与博弈相结合,提出了一种基于深度强化学习的算法——Minimax-深度Q网络(deep Q network,DQN)。该方法使用Minimax算法[16]构建线性规划来求解每个特定状态阶段博弈的纳什均衡策略,并引入DQN来更新动作状态值函数,以得到一种针对高决策水平对手的最优策略。

1 随机博弈与深度强化学习

本文为研究空战中红蓝双方战机的对抗情况,获得一种对红方有利的最优空战策略,需要用到博弈论以及深度强化学习的理论知识。

1.1 博弈论

本文研究的空战博弈实际上就是红蓝双方的对抗过程,双方的竞争性质可以利用博弈论的知识概括。博弈论是研究决策者在决策主体各方相互作用的情况下，如何进行决策以及有关该决策的均衡问题的理论[17],被广泛应用于军事问题研究。

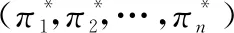
(1)

则为一个纳什均衡。

本文研究的红蓝双方战机对抗情况与追逃博弈有密切联系,追逃博弈将参与双方定义为追踪者和逃脱者,在博弈过程中博弈各方均以红方最大利益为目标,一方的得益必然导致另一方的损失,二者的得失总和为零[19],本文涉及的博弈类型也称二人零和博弈。并且追逃博弈考虑的是红方在最差情况下的对抗策略优化设计,即纵使蓝方采用非常智能的机动方式,红方仍可获得可以接受的对抗效果,且得到的结果是全局最优[20]。本文以此为研究思路,处理空战中红蓝双方战机的对抗问题,并引入深度强化学习知识。

1.2 深度强化学习

马尔可夫决策过程(Markov decision process, MDP)是指决策者周期性地或连续性地观察具有马尔可夫性的随机动态系统,序贯地作出决策[21]，即根据当前的观测状态选择一个动作执行到达下一步的状态,下一步的状态只与当前的状态和动作有关。

MDP是强化学习的基础。强化学习是智能体以“试错”的方式进行学习,通过与环境进行交互获得的奖赏指导行为,使智能体获得最大的奖赏[22]。强化学习适用于解决连续决策问题,因此可以应用于解决空战中红蓝双方战机对抗的决策问题[23]。

深度学习通过构建基于表示的多层机器学习模型,训练海量数据,学习有用特征,以达到提升识别、分类或预测的准确性[24]。深度学习具有较强的感知能力,但缺乏一定的决策力,因此将深度学习与强化学习相结合,为系统的感知决策问题提供了解决思路。

深度强化学习将深度学习与强化学习结合,用神经网络来拟合强化学习中的价值函数和策略函数,解决了强化学习状态空间较小的局限性[25]。由于本文研究的红蓝双方战机对抗的空战策略问题中,状态特征是连续多维的,因此可采用深度强化学习中基于价值函数的经典DQN算法[26]解决该问题。

1.3 随机博弈

由于空战博弈是一个动态过程,而传统博弈一般是单步的,因此需要从传统博弈拓展到随机博弈。

MDP包含一个玩家和多个状态,而矩阵博弈包含多个玩家和一个状态。对于具有多个玩家和多个状态的博弈,定义了一种MDP与矩阵博弈相结合的博弈方法,称为马尔可夫博弈,即随机博弈[27]。

随机博弈可表示为一个元组[28],(n,S,A1,A2,…，An,T,γ,R1,R2,…,Rn),其中包含的要素如下。

(1) 个数n:表示玩家数量。

(2) 状态S:状态是对环境的描述,在智能体做出动作后,状态会发生改变,其演变具有马尔可夫性。

(3) 动作A:动作是对智能体行为的描述,是决策的结果。动作空间可以是离散或连续的。

(4) 转移函数T:由给定玩家当前状态s和每个智能体的一个动作Ai控制,转移概率在[0,1]之间。

(5) 折扣因子γ:折扣因子是对未来奖励的衰减,γ∈[0,1]。

(6) 回报函数R:表示指定玩家在状态s采取联合行为(A1,A2,…,An)后在状态s′处取得的回报。

随机博弈环境中的每个智能体都由一组状态S和一组动作集A1,A2,…,Ak定义,状态转换由当前状态s和每个智能体的一个动作Ai控制,每个智能体都有一个相关的奖励函数,试图最大化其预期的折扣奖励之和。与MDP类似,随机博弈中玩家下一状态和回报只取决于当前状态和所有玩家的当前行为。求解随机博弈需要找到一个策略π,使得具有折扣因子γ的玩家的未来折扣回报最大化。

2 空战博弈建模

2.1 空战问题描述

(2)

其中航迹偏角的限制范围为[-180°,180°],滚转角的范围受实际飞机最大转弯能力限制,具体如图1所示。红方战机的目标是在蓝方战机背后取得并保持优势地位,可使用视界角(angle of aspect, AA)和天线偏转角(antenna train angle, ATA)来量化此优势位置。此外,航向交叉角(heading crossing angle, HCA)也用于描述红蓝战机之间的朝向差异。

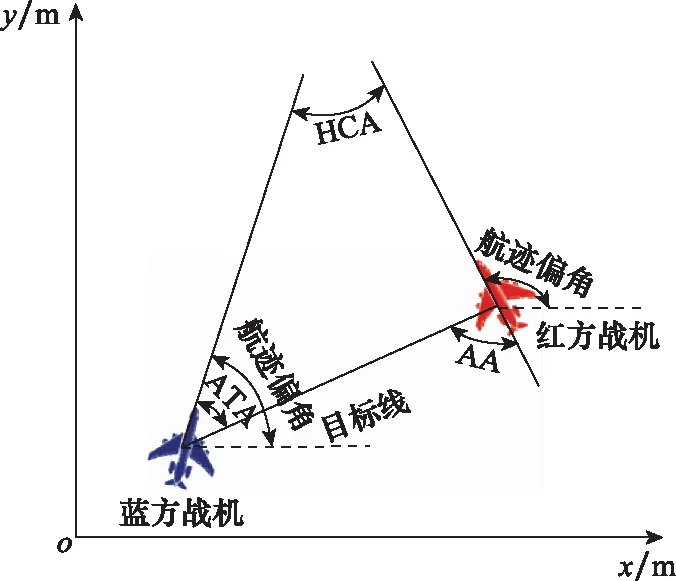
图1 红蓝双方战机相对几何关系Fig.1 Relative geometric relationship between the red and the blue fighters

2.2 随机博弈建模

本文将红蓝双方战机作为智能体,以二人零和博弈为条件对空战博弈进行建模。根据第1.2节可知,随机需要确定一个元组(n,S,A1,A2,…，An,T,γ,R1,R2,…,Rn),根据此一元组来构建空战中的随机博弈模型。

2.2.1 随机博弈模型

首先需要确定随机博弈环境中每个智能体需要的状态空间S、动作空间A和奖励函数R,智能体为当前状态s决策选择一个动作Ai到达下一个状态s′,并得到与环境交互后反馈奖励r,然后进行下一轮交互,由此实现循环。

(1) 个数n:红蓝双方战机对抗中玩家数量n为2。

由于战机的状态空间是连续无限空间,所以需要用到深度学习神经网络来处理这些特征。

(3) 动作A:战机的可选机动动作设置为向左滚转、维持滚转和向右滚转,分别用L,S,R代表这3种可选动作,构建离散的动作空间,则红方的动作空间为Ar={L,S,R},同理蓝方动作空间为Ab={L,S,R}。

(4) 转移函数T:以红方为例,红方当前状态s在红方根据策略选择的动作a与对手蓝方选择的动作o的联合行为(a,o)影响下,转移到下一状态s′的概率。

(5) 折扣因子γ:折扣因子在[0,1]中选取,一般为0.9左右。

(6) 回报函数R:在随机博弈中,使用MDP的Q值来表示即时收益。以Q(s,a,o)表示每个状态s下,己方采取动作a及蓝方采取动作o的预期奖励。根据导弹的攻击区域,设定到达导弹可攻击范围为有利态势。对于红方的奖励值r,若红方到达有利态势返回r=1,若对手蓝方到达有利态势则r=-1,其余情况r=0。

2.2.2 战机优势奖励函数

本文参考文献[29]中定义的有利态势区域来选择占位,且暂不涉及4代、5代红外近距格斗导弹的前向攻击能力[30]。以二维平面内的空战对抗为例，红方战机的优势区域,如图2所示。

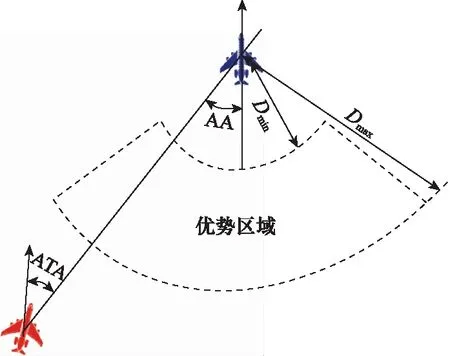
图2 红方战机优势区域Fig.2 Dominant area of the red fighter

红方战机取得优势需要满足4个条件:① 红方战机与蓝方战机的欧氏距离D在Dmin到Dmax范围内,该区域根据战机的速度和武器攻击范围决定;② 红方战机与蓝方战机的高度差H在Hmin到Hmax范围内,该范围由战机的速度和武器攻击范围决定;③ 红方战机的AA在指定视界范围内;④ 红方战机的ATA在指定ATA范围内。同时满足以上4个条件则判定红方取得优势,并获得奖励值r=1,即占据有利态势的要求如下所示:

(3)

2.2.3 随机博弈价值函数

对于多人随机博弈,已知回报函数和转移函数,期望求得其纳什均衡解,即每个智能体的联合策略,智能体的策略就是动作空间的概率分布。由于在博弈环境下,预期回报会受到对手策略的影响,而在红蓝战机空战博弈中,一般无法预测到对手的动作。在此基础上,本文采用Minimax算法选取随机博弈的最优策略。假设对手拥有高水平决策能力,在蓝方选取使红方收益最小的动作的前提下,红方选取使自己收益最大的动作,该思想与追逃博弈类似。Minimax算法的意义在于,在最坏的情况下获取最大的回报。

MDP的价值函数表示最优策略所获得的预期折扣回报和,状态值函数V(s)和状态动作值函数Q(s,a)的公式如下:

(4)

式中,T(s,a,o,s′)表示状态s经过动作a,o到达状态s′的转移概率。

由此可得,随机博弈状态s下的最优值函数V(s)可表示为

(5)

式中，PD(A)表示动作的离散概率分布。根据式(5)可以使用线性规划约束方法求得状态s下的最优策略π和最优值函数V。

对于状态s下红方动作a及蓝方动作o的动作状态值函数Q(s,a,o)为

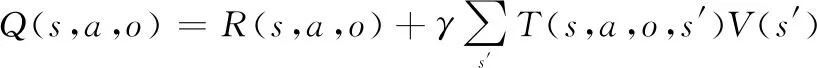
(6)

通过上述的递归方程可以经过迭代求得收敛的最优值函数,进而得到最优策略π。

由于红蓝双方战机对抗属于混合策略博弈,即博弈双方选择某一动作并不是确定的,而是对所有动作都有一个选择概率,此概率就是通过线性规划求得的最优策略π。因此本文采用轮盘赌选择法进行动作选择,个体的适应度越高,被选择的概率越大。

3 深度强化学习空战博弈实现

3.1 空战深度强化学习模型

由于在博弈情境下,转移函数难以确定,对于式(6)中使用值迭代求解MDP的传统方法涉及的状态转移函数T,可以利用强化学习中的异步更新方式Q-learning[31]替代。

Q-learning利用时间差分目标来更新当前行为值函数,每当状态s采取动作a转换到状态s′时得到奖励r进行更新:

Q(s,a)=r+γV(s′)

(7)

由于执行更新的概率正是T(s,a,s′),所以可以取代转移函数。将Q-learning的方法应用到随机博弈中,式(6)可转化为

Qt(s,a,o)=(1-α)Qt-1(s,a,o)+α(r+γV(s′))

(8)

式中,α代表学习效率。

与传统的Q-learning相比,Minimax-Q方法结合了博弈论的思想,用Minimax值替换了Q-learning中的最大值,以得到博弈条件下需要的最优策略。

此外,由第2.2节可知,红蓝双方战机对抗的空战博弈所涉及的状态为连续无限空间,所以需要用到深度学习神经网络处理特征。因此,将Minimax-Q方法进一步拓展,加入深度神经网络来逼近值函数,利用经验回放训练强化学习的学习过程,并设置独立的目标网络来处理时间差分目标。

DQN将Q-learning中的线性函数逼近以神经网络参数形式非线性逼近,可以处理空战博弈下高维度的非线性输入数据。DQN的行为值函数对应一组参数,在神经网络里对应每层网络的权重,用θ表示,更新值函数实际上就是更新θ参数[32]。

将智能体与环境交互得到的当前状态s、红方采取的动作a、蓝方采取的动作o、对应的奖励值r以及执行动作到达的下一状态s′作为一个五元组{s,a,o,r,s′}存储到记忆库。记忆库的大小是有限的,当记录库存储满后,新一组数据会覆盖记忆库中的第一组数据。从记忆库中随机抽取一定大小的数据作为训练样本,并计算出目标Q值来训练神经网络,计算目标Q值的方式即式(8)。

3.2 DQN网络训练过程

由于强化学习是试错学习,要通过环境反馈的奖励Reward来优化损失函数,损失函数为loss=(target_q-q)2,采用的优化方法为梯度下降。用神经网络逼近值函数时,若计算目标值函数的网络与梯度计算逼近值函数的网络参数相同,会因为数据的关联性导致训练结果不稳定。因此需要定义两个神经网络,目标网络与Q网络的结构完全相同,但内部的参数不同。目标网络拥有Q网络一段时间以前的参数,这组参数被固定一段时间后,再将Q网络的最新参数传递给目标网络[31]。

Minimax-DQN具体训练过程如图3所示。

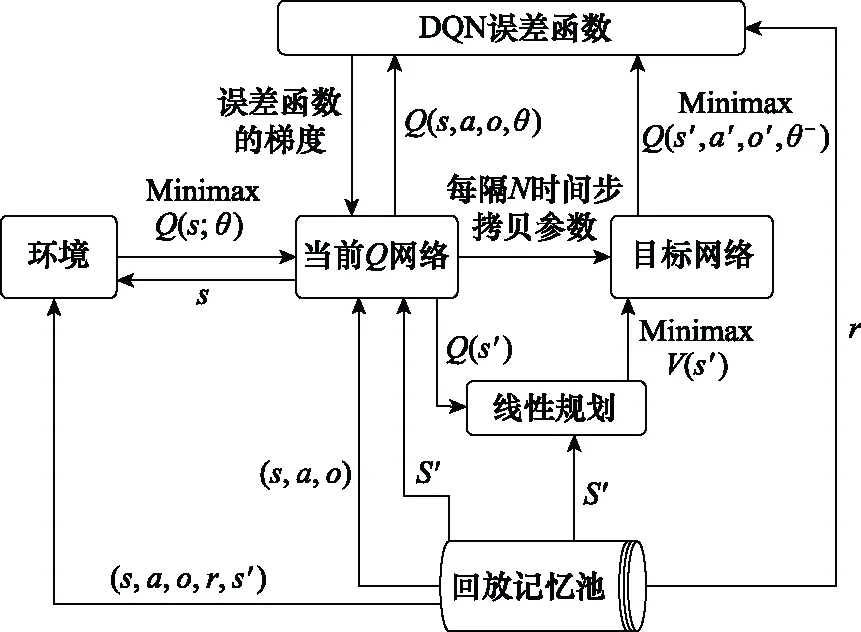
图3 Minimax-DQN训练过程示意图Fig.3 Schematic diagram of Minimax-DQN training process

3.3 Minimax-DQN算法流程

总结上述内容给出Minimax-DQN的算法步骤如下。

步骤 1初始化:给定红蓝双方一个初始状态,初始化记忆库,设置观察值。

步骤 2创建两个神经网络分别为Q网络和目标网络,Q网络参数为θ,目标网络参数θ-=θ。神经网络输入为状态s,输出为动作状态值函数Q,学习一定次数后,将Q网络的参数拷贝给目标网络。

循环遍历:

步骤 3红方智能体根据当前状态s按照策略π选择动作a并执行,得到下一状态s′以及获得的奖励r。观测蓝方智能体在状态s下选取的动作o,将{s,a,o,r,s′}五元组存储到记忆库中。依据空战态势的复杂多样性,设置记忆库存储上限为100 000组数据。

步骤 4从中记忆库中随机抽取256组数据作为一个训练样本。将训练样本的s′值作为神经网络的输入,根据神经网络输出得到状态s′下的Q(s′)。

步骤 5根据式(5)使用线性规划得到Minimax状态值V(s′),再根据式(8)计算出目标Q值target_q。

步骤 6计算损失函数

loss=(target_q-Q(s,a,o,θ))2,采用梯度下降法进行优化,更新Q网络参数。

循环结束

步骤 7根据式(5)使用训练好的神经网络输出的Q值进行线性规划求解得到最优策略π。

根据上述算法,可得到算法流程图如图4所示。

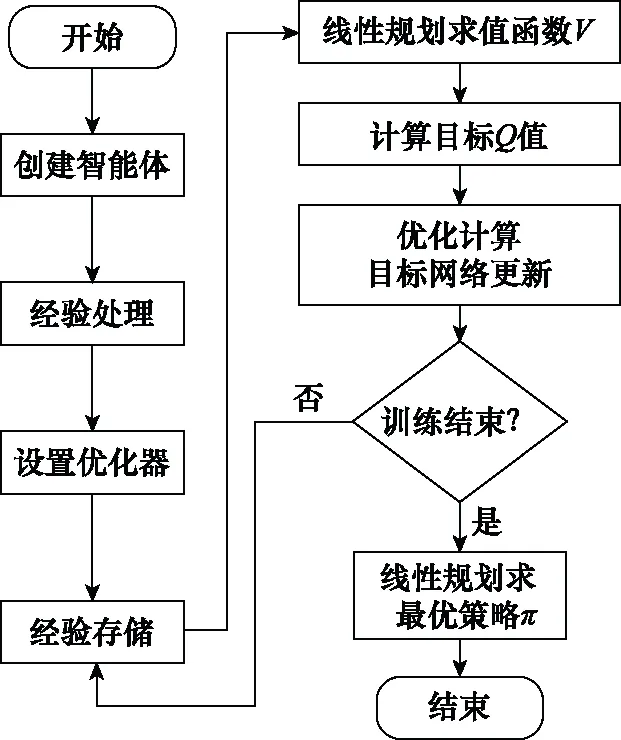
图4 Minimax-DQN算法流程图Fig.4 Flow chart of Minimax-DQN algorithm

4 仿真实验

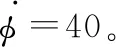
首先,红方根据Minimax-DQN算法选取策略,蓝方采用随机策略,若红方胜利则奖励值r=1,若蓝方胜利则r=-1,若飞出限定地图范围则r=0。训练10 000个回合后,停止神经网络的学习。图5为算法训练过程中的损失变化图,横坐标为训练步数,纵坐标为神经网络每次训练的损失,可以看出随着训练步数的增加,训练损失逐渐下降最终收敛趋近于0,满足了训练要求。

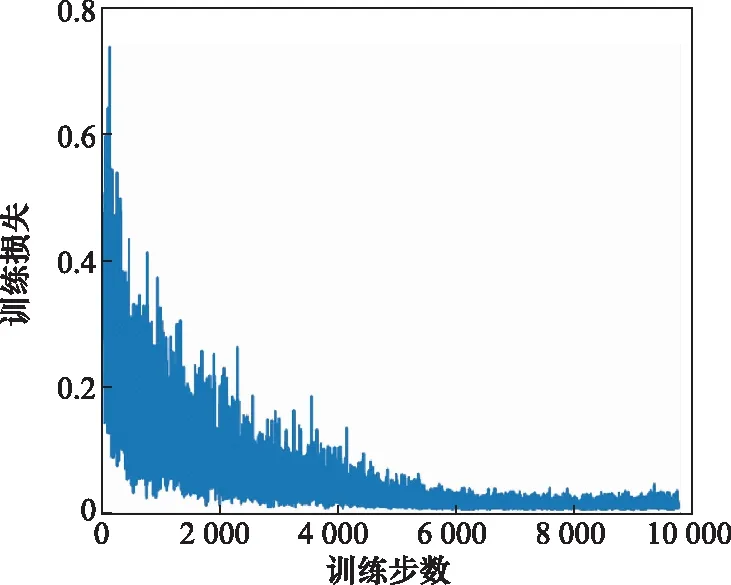
图5 网络训练损失变化图Fig.5 Change diagram of network training loss

训练完成后,红蓝双方根据价值网络得出各自策略进行1 000次博弈对抗,最终得到的博弈获胜结果如图6所示。

图6 Minimax-DQN对抗随机策略Fig.6 Confrontation between Minimax-DQN and random strategy

实验结果中,采用Minimax-DQN算法的红方获胜次数为307次,采用随机策略的蓝方获胜12次,另外有681局平局。红方在对抗中取得了较为优秀的成绩,证明了算法在博弈条件下的可行性。需要注意的是,该算法的重点是利用了线性规划求出的Minimax值函数V去更新神经网络中的Q值。本文在同样的情景条件及相同网络参数情况下,红方采用传统DQN算法选取最优策略,蓝方采用随机策略,得到的博弈结果如图7所示。其中,采用DQN算法的红方获胜次数为212次,采用随机策略蓝方获胜15次,另外有773局平局。对比图6与图7可以看出,蓝方采用的随机策略对抗性较差,而Minimax-DQN和DQN两种算法都可以在博弈情景下生成对抗策略,但Minimax-DQN算法的胜率比DQN更高,说明该算法相较DQN算法能够更准确有效地作出决策,引导战机占领有利的态势位置。

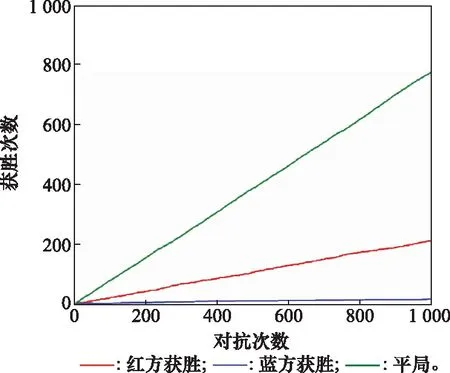
图7 DQN对抗随机策略Fig.7 Confrontation between DQN and random strategy

由于对局中平局次数较多,本文对两种算法的结果进行进一步分析,发现Minimax-DQN算法博弈结果中奖励值为0的对局，消耗的平均对抗步数约为45步,而DQN算法相同情况消耗的平均对抗步数约为82步。下面对双方奖励值为0的具有代表性的对局进行可视化，如图8所示。对比图8两种算法的对局可以发现,Minimax-DQN算法达成平局主要是由于在红方达到优势区域前飞出了限定地图范围,因此平均步数较小。而DQN算法存在无法针对对手动作采取有效对抗策略的问题,因此在地图中消耗的步数更大。

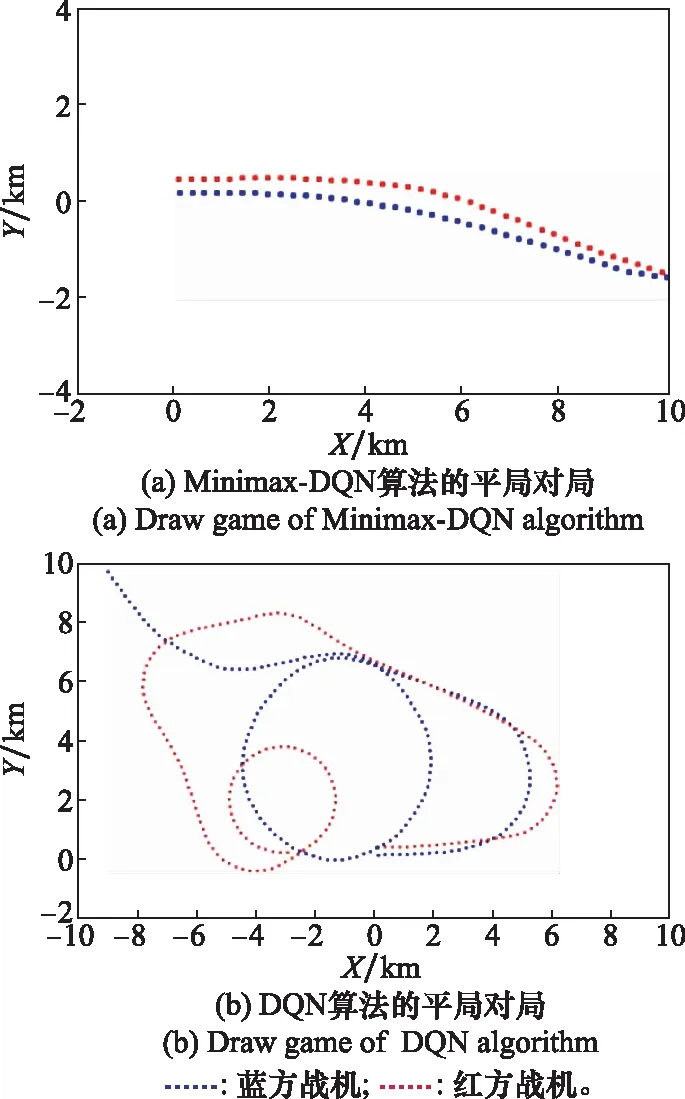
图8 两种算法的平局对局Fig.8 Draw game of two algorithms

接下来,将上述两种算法进行对抗比较,红方智能体采用Minimax-DQN算法训练后的网络生成策略,而蓝方智能体采取DQN算法生成策略进行博弈对抗1 000次,得到的博弈结果如下图9所示。

图9 Minimax-DQN对抗DQNFig.9 Confrontation between Minimax-DQN and DQN

图9的实验结果中,采用Minimax-DQN算法的红方获胜次数为501次,采用DQN算法的蓝方获胜49次,另外有450局平局。对比图6可以发现,Minimax-DQN算法的获胜次数增加,平局数减少,在对手实力越强的情况下算法表现越好,验证了Minimax算法在最坏情况下表现出最大回报的性质。

图10为红方随机生成一个初始态势后与蓝方进行博弈对抗的仿真可视化轨迹图。图11为对抗过程中红方战机的状态变量图。可以看到，红方战机不断调整自己的状态最终占据了优势地位。

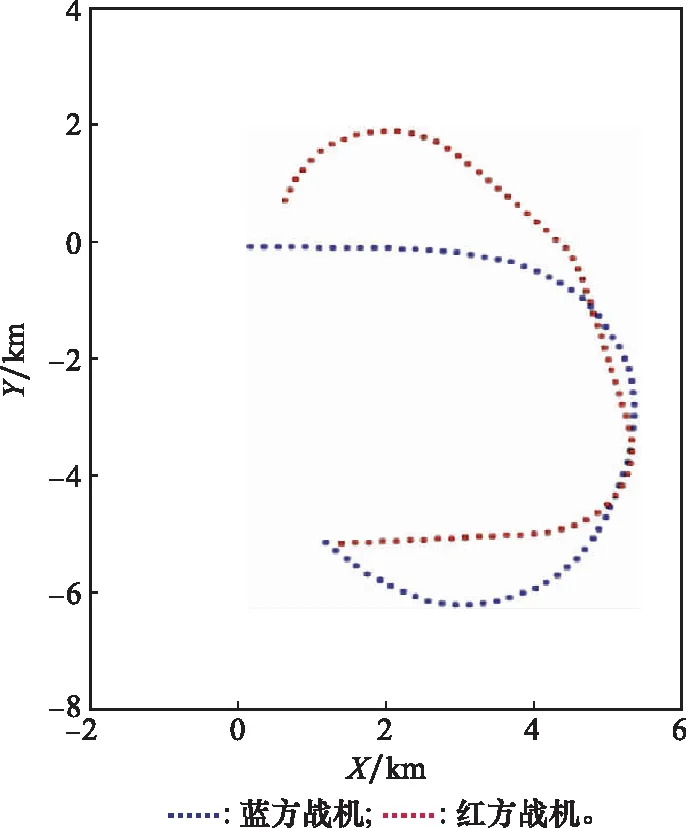
图10 红方随机态势下的博弈对抗轨迹Fig.10 Game confrontation trajectory under the red random state

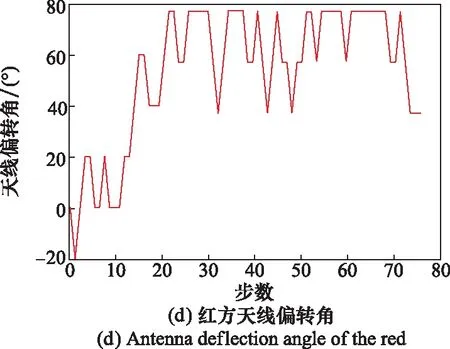
图11 红方战机状态变量Fig.11 State variables of the red fighter

为了测试4种典型初始态势下,红蓝双方的博弈对抗情况,进行了仿真测试如图12所示,4组对局分别为红方优势对局、红方劣势对局、双方均势对局和双方中立对局。

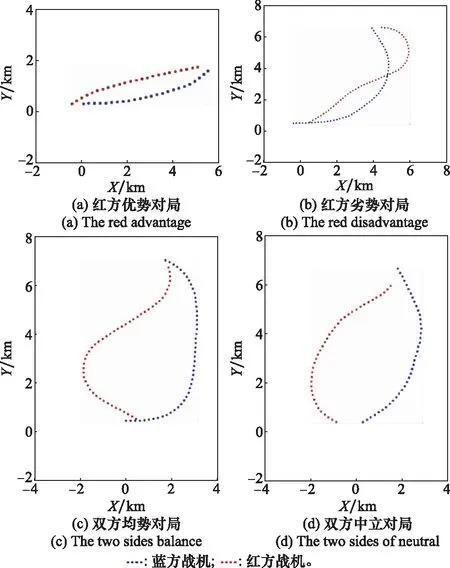
图12 博弈对抗轨迹Fig.12 Trajectory of game confrontation

图12(a)中,红方战机初始坐标位于蓝方战机西方500 m处,航迹偏角φb=30°,两机距离小,红方战机达到攻击蓝机条件,红方处于优势。可以看出蓝方战机想掉头改变局势,但被红方战机利用初始位置的优势拦截,红方率先达到优势态势。图12(b)中，红方战机初始坐标位于蓝方战机东方500 m处,航迹偏角φb=30°,两机距离小,蓝方战机达到攻击红机条件,红方处于劣势。可以看出红方战机率先掉头改变局势,利用角度偏差最终扭转局面获得胜利。图12(c)中，红方战机初始坐标位于蓝方战机东方500 m处,航迹偏角φb=150°,两机距离小,双方均达到攻击对方条件,两机处于均势。红蓝双方同时转向,红方率先拉近距离并取得角度优势,最终获胜。图12(d)中红方战机初始坐标位于蓝方战机西方1 000 m处,航迹偏角φb=150°,两机距离大,双方均不满足攻击对方条件,两机处于均势。可以看出依旧是红方率先拉近距离,从左后方占据优势态势。

由4组仿真实验可以看出,红方能在任意初始态势下,利用决策最终占据有利态势,验证了算法的有效性。

结合上述仿真实验结果及对比分析,Minimax-DQN算法结合了博弈思想来更新神经网络值函数,具有较好的适应性和智能性,能够在博弈场景下准确地作出有效决策来引导战机占据有利的态势位置。

5 结 论

本文采用深度强化学习与博弈相结合的方法,提出了一种可解决空战中红蓝双方战机对抗机动决策问题的算法,即Minimax-DQN算法。该算法利用深度学习神经网络来处理空战中战机高维连续的态势特征,并引入强化学习决策模型,通过与环境交互训练智能体,最后采用Minimax算法构建线性规划求解出纳什均衡策略,得到战机的最优机动决策。

目前本文通过空战仿真实验验证了算法的可行性,下一步的工作将加入高度影响，将仿真环境从二维拓展到三维,并考虑雷达和武器情况进行现代空战的研究,使算法适应更加复杂的战场环境,还将由一对一空战决策问题拓展到多对多的集群协同作战中的博弈智能问题研究。