基于OFDM-LFM的弹载广域SAR成像距离模糊抑制
2021-01-26鲍雨婷张鹍鹏占必超李君宜占建伟
鲍雨婷, 曹 菲, 张鹍鹏, 占必超, 李君宜, 占建伟
(1. 火箭军工程大学核工程学院, 陕西 西安 710025; 2. 北京遥感设备研究所, 北京 100854)
0 引 言
传统合成孔径雷达(synthetic aperture radar, SAR)成像一直存在着宽测绘带下距离向模糊的问题[1-2],降低脉冲重复频率(pulse repetition frequency,PRF)可以抑制距离模糊,但PRF低于回波多普勒带宽会造成方位模糊[3]。在不降低PRF的情况下,已有学者研究抑制距离模糊的方案[4-9]。文献[4]提出交替发射正负线性调频(linear frequency modulation, LFM)信号,利用失配滤波造成模糊信号的散焦,可显著改善点状目标和分布式目标的距离模糊。文献[5]利用方位向相位编码(azimuth phase coding,APC)技术对不同发射脉冲进行相位编码,在频域上滤除距离模糊信号的频谱。文献[6]采用脉冲块编码技术,可以在匹配滤波时检测出距离模糊造成的虚假目标。文献[7-9]提出利用正交频分复用(orthogonal frequency division multiplexing, OFDM)信号及其编码信号抑制距离模糊。文献[10]提出以LFM信号为基的OFDM-LFM信号用于高脉冲重复频率SAR。文献[11]提出用随机矩阵调制的方法对OFDM-LFM进行优化,产生了高距离分辨率、大时间带宽积、低峰均比的波形,但是波形正交性不足,信号间互相关峰值过大,难以有效抑制距离模糊,且能产生的正交信号个数和子载波个数相等。
上述方案应用在弹载广域SAR成像上时,无法有效抑制距离模糊。高弹道弹载SAR在对海上中大型舰艇目标进行快速广域成像时,同时具备星载SAR的高弹道高度和传统弹载SAR的高机动速度,在针对海上中大型运动目标的精确制导问题中具有重要研究价值。但在研究中发现,由于平台的高弹道高度、高机动速度特性,造成两个新的问题: ① 平台高度相对于传统弹道导弹大幅提高,发射脉冲所需的往返时间随之变大,第n个发射脉冲的回波信号在第n+k个脉冲周期被接收到,k值进一步变大,导致更复杂的距离模糊特性;② 弹载平台的高速度特性使平台在一个脉冲重复周期内飞过更远的距离,目标跨距离单元走动,且对回波信号进行脉压时受频偏影响变大。以上特点导致文献[4-11]中提出的方案无法解决弹载广域SAR成像中的距离模糊问题。
针对上述问题,需要对发射波形进行优化设计,满足大时间带宽积和低峰均比特性的基础上,对正交性能提出更高要求。进一步提升波形间的正交性,并增加相互正交的波形数量。本文研究了基于混沌序列调制的OFDM-LFM信号,可以产生任意长度和更多数量的信号,仿真结果表明,信号间的互相关性进一步降低,正交性增强,并且具有良好的模糊特性。
1 信号设计方案
1.1 信号模型
图1为弹载广域SAR成像示意图,导弹平台以速度v沿方位向飞行。为实现对海上中大型舰艇目标进行快速巡回成像,导弹飞行高度相对于传统弹载成像雷达由h1大幅提升至h2,发射脉冲到达目标点及回波被接收机接收的时间变长。
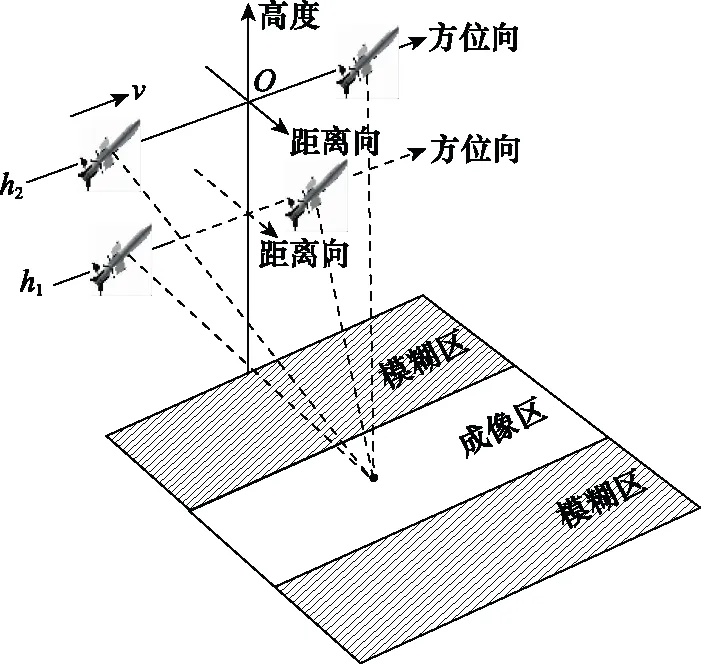
图1 弹载广域SAR成像场景Fig.1 Missile-borne SAR wide area imaging scene
如图2所示,信号sn(t)的回波echon(t)在sn+k(t)脉冲周期才被接收,k值进一步变大。sn+k(t)脉冲周期内,除目标成像区对脉冲sn(t)的散射回波外,还混叠了模糊区的散射回波echon-1(t)、echon+1(t)等,导致严重的距离向模糊问题。若发射信号间满足正交性,则可通过匹配滤波对不发射信号的回波进行区分,从而抑制距离模糊。实际中难以产生绝对正交的信号,研究人员着力于提高伪正交信号的正交性能。由于k值的增大,对相互正交的发射信号的数量也提出了更高要求。本文建立了基于混沌序列调制的OFDM-LFM信号模型,提高发射信号正交性能,同时增大正交信号数量。

图2 发射信号回波混叠图Fig.2 Transmit signal echo overlap
信号以载频f0传输,每个脉冲信号有N个码元,每个码元有M个子载波,则发射的信号表达式为
(1)
若每个码元只包含一个子载波,则表达式为
exp[j2πFn(t-nTs)+jπKn(t-nTs)2]
(2)
式中,si(t)(i=1,2,…,I)是发射的I个相互正交的脉冲信号;系数An(t)为第n个码元的包络,采用矩形窗函数,表达式为
(3)
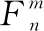
(4)
(5)
基带信号可表示为
exp[j2πpnmΔf(t-nTs)+jπqnmk(t-nTs)2]
(6)
式中,pnm是由混沌序列映射得出的频率调制系数。线性调频率系数qnm∈{-1,1}。若qmn=1,则信号采用正调频率OFDM-LFM基;若qmn=-1,则信号采用负调频率基;若qmn在1和-1间交替变换,则信号采用混合调频率基。
1.2 基于Bernulli映射的混沌调制序列模型
混沌系统作为一种特殊的非线性动力学系统,可产生非周期随机信号,具有可控制、可同步、可重现以及长度不受限的特点。混沌系统的连续功率谱、内随机、类噪声等优良特性使它逐渐被引入到雷达波形设计领域中[12-17]。离散混沌系统有Logistic映射、Bernulli映射、tent映射和chebyshev映射等多种映射方式,本文采用的是基于Bernulli映射的一维离散混沌系统。Bernulli映射序列结构可表示为
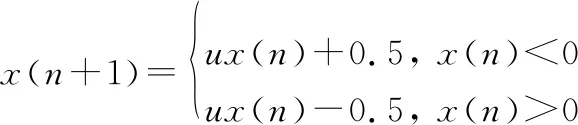
(7)
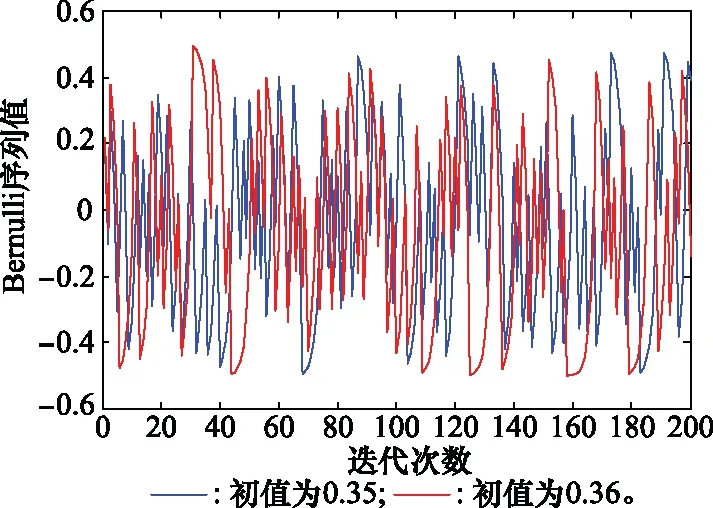
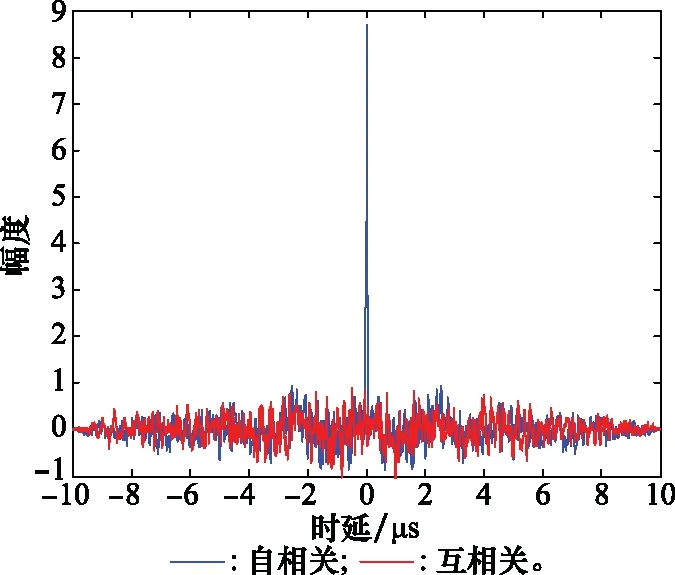
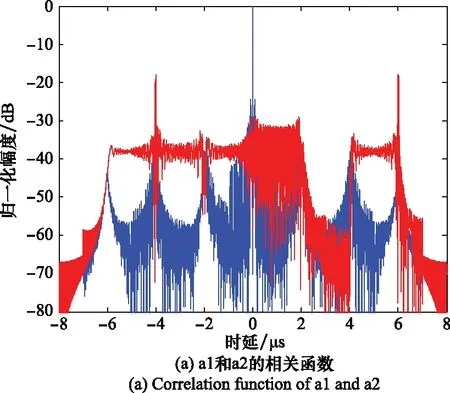
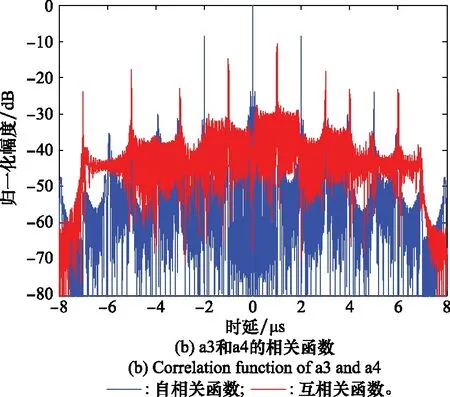
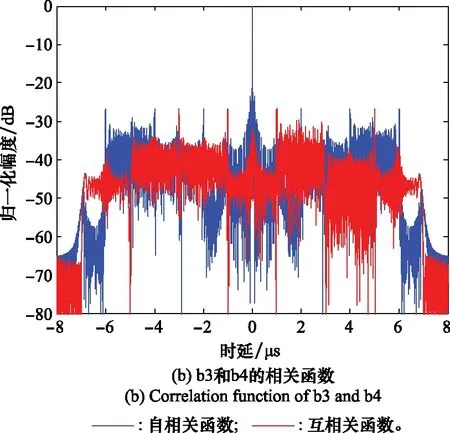
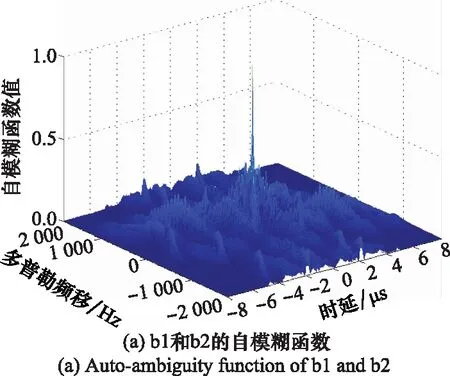
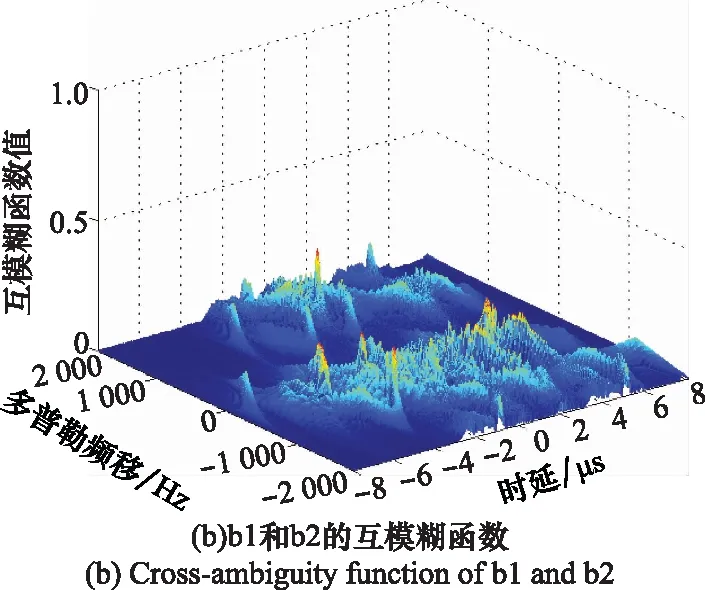
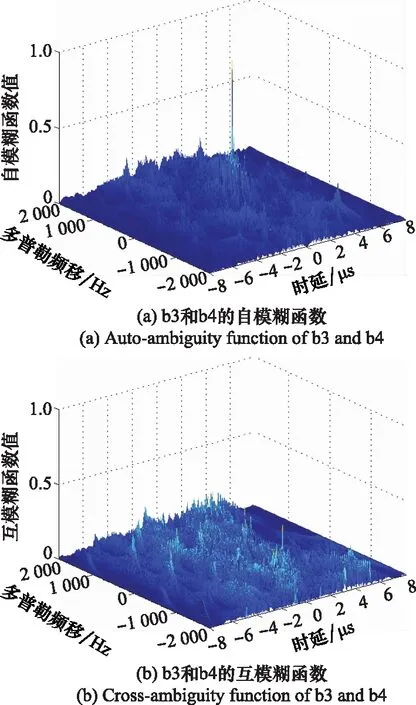
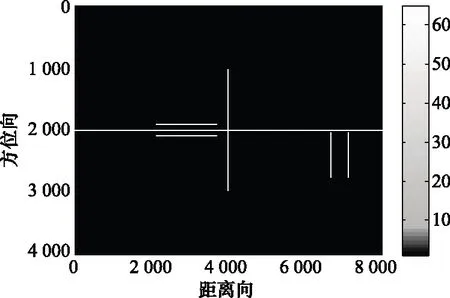
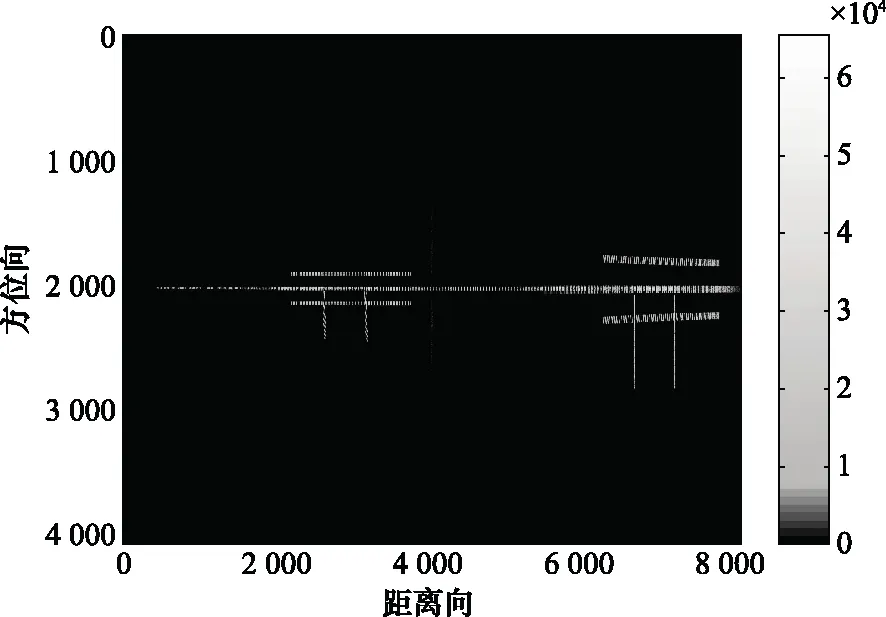
式中,u为控制参数,取值范围为1 图3 Bernulli映射序列的倍周期分岔图Fig.3 Period-doubling bifurcation diagram of Bernulli mapping sequence 从图3中可以看出,随着u的变大,混沌序列从平衡态进入周期态,最后进入混沌状态。初始值越接近2,混沌特性越明显。 对初始值的高度敏感,使得混沌系统区别于其他运动系统,拥有长期不可预测特性。图4是控制参数u=1.999,初始值分别为x(0)=0.35和x(0)=0.36时产生的Bernulli映射序列时域波形图,从图中可看出两个相差极小的初值产生的两条混沌轨迹有很大的区别。 图4 Bernulli序列时域波形Fig.4 Bernulli sequence time domain waveform 图5是Bernulli映射序列的自相关和互相关函数图,从图中可以看出,自相关函数逼近冲击函数,并且互相关电平接近0,表明Bernulli映射序列具备良好的正交性能。 图5 Bernulli序列相关函数Fig.5 Correlation function of Bernulli sequence 基于Bernulli映射产生长度为M0+MN的混沌序列,为尽可能排除初始值造成的影响,舍弃前M0个序列值。即可得到M段长度为N的序列,表示为 (8) 式中,M为需要产生的正交脉冲信号个数,取第m段混沌序列xm,构造xm与频率调制系数pmn的映射为 {x(m-1)N+1,x(m-1)N+2,…,xmN}↔{pm1,pm2,…,pmN} (9) 由Bernulli映射得到的xmn值在-0.5到0.5之间,将第m段中的序列值按照从小到大的顺序排列,最小值编号为0,依次递增,最大值编号为N-1。即可得到第m个脉冲信号的频率调制系数序列{pmn|pmn∈[0,1,…,N-1]}。 信号s(t)的模糊函数定义为 (10) 式中,τ为时延;fd为多普勒频率;*表示共轭运算。以下用基带信号分析各项性能,将式(6)代入式(10)可得 χi, j(τ,fd)= (11) 式中, (12) 当i=j时,函数χ(τ,fd)为自模糊函数,当i≠j时,为互模糊函数。信号的模糊函数可以反映信号在速度、距离分辨率以及杂波抑制等方面的性能,理想的模糊函数接近于冲击函数呈图钉形,自模糊函数旁瓣值和互模糊函数值越低,信号设计效果越好。 当多普勒频移fd=0时,雷达模糊函数就转变为信号的相关函数: (13) 弹载广域SAR成像时,在某脉冲重复周期内,雷达接收到的回波信号会包含前几个周期的信号回波,造成严重的回波混叠。若想利用匹配滤波器对混叠的回波进行分离,需要发射的脉冲信号间具有良好的正交性能。理想正交波形的自相关函数为冲击函数形式,互相关函数为零,然而理想正交波形在实际中难以获得。实际中相关函数的互相关值越低,信号的正交性能越好。此外,由于能量强的旁瓣会淹没附近的弱小目标,还需要避免过高的自相关旁瓣。 文献[11]中采用的是随机二值矩阵调制的OFDM-LFM信号,随机二值矩阵产生的信号编码系数如表1所示。 表1 传统OFDM-LFM信号的编码系数 本文提出的基于混沌序列调制的OFDM-LFM信号混沌调制编码系数如表2所示。 表2 改进OFDM-LFM信号的编码系数 表2中的两组信号设计流程及波形优选方法如下。 步骤 1非线性动力学系统采用Bernulli映射产生长度为M0+MN的混沌序列集; 步骤 2舍弃序列集中的前M0个点,排除初始值对混沌性能的影响,得到M段长度为N的序列; 步骤 3将每段序列按大小一一映射为0到N-1的频率调制系数; 步骤 4选定正负交替的LFM斜率系数; 步骤 5用步骤3和步骤4得到的频率调制系数和LFM斜率系数对OFDM-LFM信号基底进行调制,生成基带信号; 步骤 6以最小化互相关峰值电平与自相关峰值旁瓣电平之和为准则进行波形优选。 采用上述步骤可获得较多组正交性能优良的信号,以下仅列出其中两组与传统信号进行对比。信号a1、a2、a3、a4、b1、b2、b3、b4均含有8个码元,其中,a1、a2、b1、b2的每个码元含有一个子载波,a3、a4、b3、b4的每个码元含有两个子载波。表中pnm和qnm分别为混沌调制频率的编码系数和LFM斜率的编码系数。信号采用正负交替的混合LFM斜率。 图6为传统OFDM-LFM信号的相关函数图,图6(a)为a1的自相关函数图和a1、a2的互相关函数图,图6(b)为a3的自相关函数图和a3、a4的互相关函数图。 图6 传统OFDM-LFM信号的相关函数Fig.6 Correlation functions of traditional OFDM-LFM signal 从图6中可以看出,采用随机二值矩阵调制的信号互相关旁瓣电平比较高,且在某些位置会出现接近于自相关电平的峰值。图7为改进OFDM-LFM信号的相关函数图,图7(a)为b1的自相关函数图和b1与b2的互相关函数图,图7(b)为b3的自相关函数图和b3与b4的互相关函数图。 图7 改进OFDM-LFM信号的相关函数Fig.7 Correlation function of improved OFDM-LFM signal 图6中传统OFDM-LFM信号的自相关函数存在许多高旁瓣,这些高旁瓣可能会被误判为小目标。互相关函数的峰值电平较高,信号之间的正交性不够。从图7可以看出,采用混沌序列调制的信号没有明显的高旁瓣,且互相关旁瓣电平也大幅降低。通过对比可发现,a1、a2、b1和b2的相关函数表现明显优于a3、a4、b3和b4。 为深入探讨所提方案的性能,表3列出了传统信号和改进信号的自相关峰值旁瓣电平(autocorrelation peak sidelobe level,APSL)和互相关峰值电平(cross-correlation peak level,CPL)。 表3 传统信号和改进信号对比 将表3中传统信号和改进信号的电平值进行对比,信号每个码元只含一个子载波时,CPL值由-18.06 dB降低至-32.24 dB,正交性能大幅提升,APSL值升高了约2 dB。信号每个码元含两个子载波时,改进信号的性能提升幅度更大,APSL和CPL的电平值降低了2~3倍。表3表明,改进信号在CPL和APSL上的表现优于传统信号。 改进信号的模糊函数图如图8和图9所示,可看出自模糊函数呈现类图钉状特性,旁瓣幅值相对于主瓣幅值很小,互模糊函数也具备低峰值电平的特点,说明信号在改善了相关特性的同时,还保持着良好的模糊特性。 图8 改进信号b1和b2的模糊函数Fig.8 Ambiguity function of improved signal b1 and b2 图9 改进信号b3和b4的模糊函数Fig.9 Ambiguity functions of improved signal b3 and b4 为验证改进的OFDM-LFM信号在抑制广域SAR成像距离模糊方面的有效性,分别以传统OFDM-LFM信号和改进OFDM-LFM信号为发射信号,采用后向投影(back-projection, BP)成像算法对分布式目标进行成像,通过观察成像结果来验证方案的有效性。基于本文提出的弹载广域SAR成像背景,平台具有高机动速度和高弹道高度特点,对分布式目标进行仿真成像的参数如表4所示,分布式目标场景如图10所示,场景大小4 096×8 192,场景中心布置了中心十字,十字以外有两条短横线和短竖线。 表4 弹载广域SAR成像参数 图10 分布式目标场景Fig.10 Distributed targets scene 分别将随机二值矩阵调制的OFDM-LFM信号和混沌序列调制的OFDM-LFM信号作为发射信号,经过回波模拟模块后得到回波数据,采用BP成像算法对目标场景进行仿真成像。图11和图12分别为传统信号和改进信号的成像结果。 图11 传统信号分布式目标成像结果Fig.11 Distributed targets imaging result of traditional signals 图12 改进信号分布式目标成像结果Fig.12 Distributed targets imaging result of improved signals 从图11中可看出,随机二值矩阵调制的信号成像后在距离向模糊现象严重,两条短横线在中心十字右侧存在明显模糊图像,两条短竖线在中心十字左侧存在明显模糊图像。图12中混沌序列调制的信号成像结果显示,距离向的模糊图像得到有效抑制,成像质量有明显的提升。 将混沌序列应用于信号调制设计中,易获得任意编码长度和众多数量的具有准正交特性的信号。对信号设计模型、模糊函数及相关函数进行理论和仿真分析,基于Bernulli映射的混沌序列调制的OFDM-LFM信号由于引入混沌带来的随机性,进一步降低了信号的互相关峰值电平和自相关峰值旁瓣电平,提高了发射脉冲间的正交性,信号模糊函数也表现出类似“图钉型”的理想形状。分布式目标成像仿真结果证明,混沌序列调制的OFDM-LFM信号可有效解决弹载广域SAR成像中的距离模糊问题。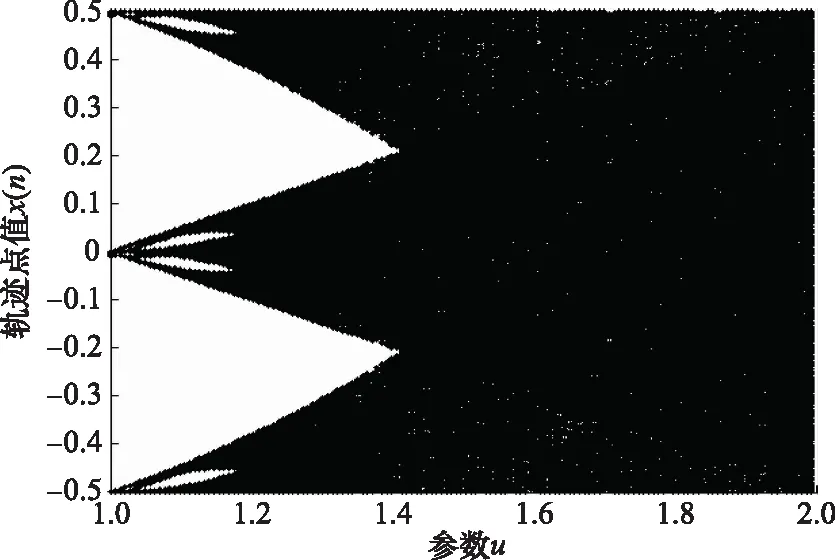
2 性能分析
2.1 模糊函数
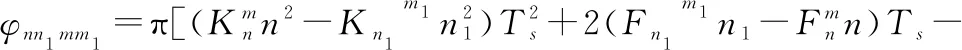
2.2 相关函数
3 波形实现及仿真分析
3.1 波形实现及性能仿真




3.2 成像仿真


4 结 论
