基于改进3D-ESPRIT算法的GTD模型参数估计与目标识别

徐嘉华, 张小宽, 郑舒予, 宗彬锋, 郑书昌

(1. 空军工程大学防空反导学院, 陕西 西安 710051; 2. 空军工程大学研究生院, 陕西 西安 710051; 3. 西安建筑科技大学, 陕西 西安 710055)

0 引 言

几何绕射理论(geometric theory of diffraction, GTD)模型是一种可有效描述雷达目标电磁散射特性的散射中心模型。该模型的核心机理为:在高频区,雷达目标散射回波可近似为多个强散射中心相干叠加[1]。GTD散射中心模型为传统点散射中心模型的改进模型,其在雷达目标识别[2-4]、雷达散射面积(radar cross section, RCS)频率内插与外推[5]、雷达目标三维重构[6-7]等军事领域均有着十分广泛的应用前景。

通过雷达目标的电磁散射回波数据准确估计出GTD模型参数并以此进行数据重构,对雷达目标电磁散射特性的刻画显得尤为重要。针对此类模型参数估计问题,国内外研究者利用如多重信号分类算法[8-10]、基于旋转不变技术的信号参数估计(estimating signal parameter via rotational invariance techniques, ESPRIT)算法[11-14]、增广矩阵束算法[15]等对参数进行估计提取。

GTD模型从维度的角度可分为一维、二维及三维模型。随着维度的增大,GTD模型对目标电磁散射特性的刻画愈加精准,但算法的运算复杂度也随之增加。目前多数研究者主要针对一维GTD、二维GTD模型进行参数估计提取,对三维GTD模型参数估计问题涉及甚少。对此，本文利用经典的三维ESPRIT(three-dimensional ESPRIT, 3D-ESPRIT)算法对三维GTD模型进行参数估计提取。

经典3D-ESPRIT算法可较为准确地估计得到三维GTD模型参数,但当外界环境的噪声较高时,算法的参数估计性能会显著降低。为解决这一问题,提出了基于平方前后向平滑的3D-ESPRIT(quadratic-forward-backward-3D-ESPRIT, Q-FB-3D-ESPRIT)算法,该算法较之前算法,在噪声鲁棒性和参数提取精度两个方面进行了优化。为了进一步提高对目标回波数据的利用,受到文献[16]的启发,本文提出一种改进算法。首先,将目标的极化信息以极化散射矩阵的方式加到三维GTD模型中；其次，对协方差矩阵进行前后向平滑处理；最后，对总协方差矩阵取平方处理。该算法是在Q-FB-3D-ESPRIT中加入了极化信息,即极化Q-FB-3D-ESPRIT(polarized Q-FB-3D-ESPRIT, PQ-FB-3D-ESPRIT)。改进算法更加充分地利用了数据,进一步提高了算法的参数估计性能与噪声鲁棒性。除此之外,本文还对基于GTD散射中心模型的雷达目标识别技术进行了研究,仿真结果验证了该方法的可行性。

1 三维GTD模型

根据文献[17]提出的三维GTD散射中心模型,目标后向电磁散射数据可等效为I个强散射中心叠加合成的,其数学表述为

E(fm,θn,φk)=

yisinθcosφ+zisinφ)/c]+ω(fm,θn,φk)

(1)

式中,E(fm,θn,φk)表示雷达目标电磁散射回波;I表示雷达目标近似的散射中心个数；参数{Ai,αi,xi,yi,zi}分别表示第i个散射中心的散射强度、散射类型、X轴距离、Y轴距离及Z轴距离;fm=f0+mΔf,m=1,2,…,M,f0为最低频率,Δf为步进频率,m为步进数量,M为总频率个数;θn=θ0+nΔθ,n=1,2,…,N,θ0为起始方位角,Δθ为步进方位角,n为方位角下标,N表示总方位角个数;φk=φ0+kΔφ,k=0,1,…,K,φ0为起始俯仰角,Δφ为步进俯仰角,k为俯仰角下标,K为总俯仰角个数;nΔθ和kΔφ分别为方位方向上的小转角和俯仰方向上的小转角；c=3×108m/s为电磁波传播速度；ω(fm,θn,φk)为复高斯白噪声；αi为0.5的整数倍[1],根据不同散射体可分为5种[18],分别为-1,-0.5,0,0,5,1。

对于GTD散射中心参数模型化简的过程,在文献[17]中均详细给出,因此本文不在赘述,直接给出求解散射中心模型各参数的数学解析式分别为

(2)

(3)

(4)

(5)

式中,angle(·)表示计算复数的相位角;

(6)

(7)

(8)

在完成上述参数求解过程后,基于最小二乘法对散射中心强度Ai进行参数提取,具体过程如下:

(9)

(10)

式中,

G=[a1,a2,…,aI]

(11)

ai=[ai(0,0,0),ai(1,0,0),…,ai(M-1,0,0),ai(0,1,0),…,
ai(M-1,1,0),…,ai(M-1,N-1,0),
ai(0,0,1),…,ai(M-1,N-1,K-1)]T

(12)

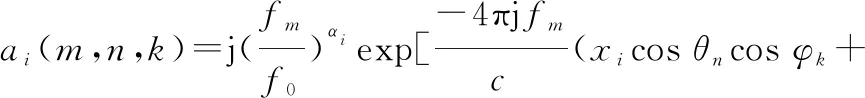
(13)

Ek=[E(f0,θ0,φ0),…,E(fM-1,θ0,φ0),ai(f0,θ1,φ0),…,
ai(fM-1,θ1,φ0),…,ai(fM-1,θN-1,φ0),
ai(f0,θ0,φ1),…,ai(fM-1,θN-1,φK-1)]

(14)

2 改进3D-ESPRIT算法

针对经典3D-ESPRIT算法在低信噪比(signal to noise ratio, SNR)时参数估计降低和噪声鲁棒性差的问题,本文改进的PQ-FB-3D-ESPRIT算法主要对经典3D-ESPRIT算法[19]前两个步骤进行改进,以提高算法的参数估计性能。具体改进如下。

步骤 1计算极化条件下仿真目标电磁散射数据。通过将3D-ESPRIT模型中的散射强度A替换为极化散射系数Si,p,即可完成极化条件下的3D-ESPRIT模型的构建,其具体表达式如下:

(15)

式中,Si,p表示第i个散射中心在p极化方式下的散射系数,p∈{hh,hv,vh,vv}表示4种极化方式[2]。其中一些典型结构的散射矩阵在文献[18]均有给出,不在赘述。

步骤 2前后向平滑处理。对计算得到的目标极化电磁散射数据进行前后向空间平滑处理,获得新的总协方差矩阵为

(16)

式中,

Y=JEk

为一PQ×PQ置换矩阵,其为反单位矩阵。

步骤 3平方处理。由式(16)可知,总协方差矩阵R为Hermittan矩阵,因此矩阵R1和R两者的特征值与特征向量具有以下关系:

(17)

式中,矩阵R1与R的特征值为分别λ1和λ;矩阵R1与R的特征向量分别为Λ1和Λ。

通过R1替换R,可在不改变原有特征向量的条件下,增大信号特征值与噪声特征值之间的差距。从数学关系上来看,各参数的方差可表示为

(18)

式中,μi为第i实验得到的散射中心参数;μ为假设的散射中心参数;σ2为噪声对应的特征值;γm为信号对应的特征值[16]。

R1=RRH=R2

(19)

对新的总协方差矩阵R1作3D-ESPRIT算法中的一系列处理,即可估计得到三维GTD模型中的各参数值。

本文改进算法仅对经典3D-ESPRIT算法协方差矩阵的构造作了改进。因此,本节仅将此步骤的运算量作比较分析[16],具体如表1所示。

表1 构造协方差矩阵的计算量比较

比较表1可知,经典的3D-ESPRIT算法在协方差矩阵构造[20]步骤的运算量为P2Q2L2(M-P+1)(N-Q+1)(K-L+1),Q-FB-3D-ESPRIT算法在此步骤的运算量为(3P2Q2L2+PQL)(M-P+1)(N-Q+1)(K-L+1)+P3Q3L3。而本文提出的改进3D-ESPRIT算法在此步骤的运算量为4[(3P2Q2L2+PQL)(M-P+1)(N-Q+1)·(K-L+1)+P3Q3L3]。

由此可见,本文的改进算法在构造协方差矩阵步骤的运算量要稍大于经典3D-ESPRIT算法与Q-FB-3D-ESPRIT算法。分析原因可知,本文改进算法增加了对目标极化散射信息的利用与数据的利用率,因此算法的运算量会略有增加。

3 基于GTD模型匹配的目标识别

首先，计算目标全方位角对应的电磁散射数据,再利用本文改进的3D-ESPRIT算法对模型参数进行估计,构建全方位角下的三维GTD散射中心模型,以此作为目标的识别模板。其次，获取目标在任意方位角下的电磁散射数据,利用改进3D-ESPRIT算法估计其对应的散射中心模型参数，并构建三维GTD散射中心模型,以此作为待测样本。最后,利用智能算法如支持向量机算法等[20-24]对上述两种模型进行匹配,从而达到目标识别的目的。其具体流程如图1所示。

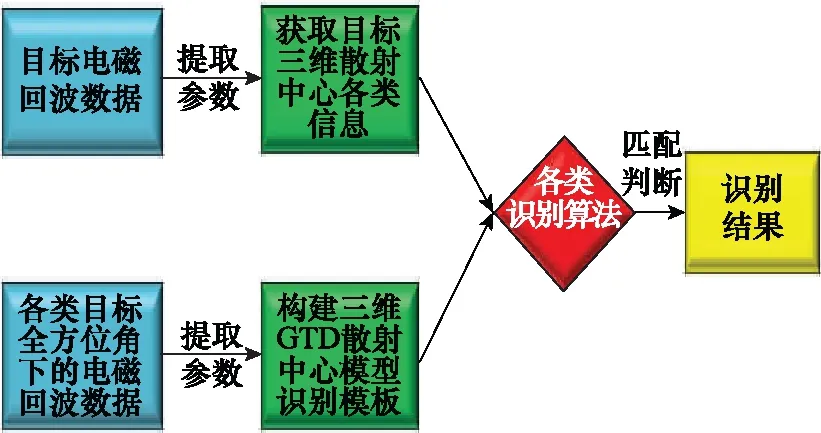
图1 基于GTD模型的目标识别实现流程Fig.1 Implementation process of target recognition based on GTD model

4 仿真实验

本文用4个散射中心合成目标的电磁散射回波数据,以验证本文提出的改进算法的参数估计性能以及基于GTD散射中心模型进行目标识别方法的可行性。首先产生目标的后向电磁散射数据:设定雷达的工作频率f0的范围为10～10.16 GHz,以16 MHz为步进,选择11个频点;方位角θ0和俯仰角φ0均为90°,角度间隔均为0.01°,总方位角度数N=11,总俯仰角度数K=11[20]。依次设置4个散射中心为单次反射、二面角、圆柱体及左旋极化,具体散射矩阵及4个散射中心对应的各模型参数如表2所示。且在回波数据中加入-10～20 dB的噪声,其中SNR为

(20)

表2 散射中心参数

仿真实验 1为比较在不同SNR下本文改进算法与其他算法的参数估计性能,在-10～20 dB中等间隔选取7个SNR条件,并在每一SNR下,经过多次蒙特卡罗实验,获得估计参数与实际参数的均方根误差(root mean squared error, RMSE),仿真结果如图2～图6所示。

图2 横向距离x的RMSE比较Fig.2 RMSE comparison of transverse distance x

图3 纵向距离y的RMSE比较Fig.3 RMSE comparison of longitudinal distance y

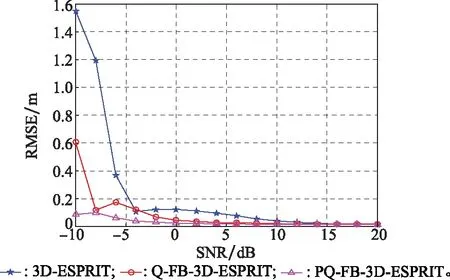
图4 垂直距离z的RMSE比较Fig.4 RMSE comparison of vertical distance z

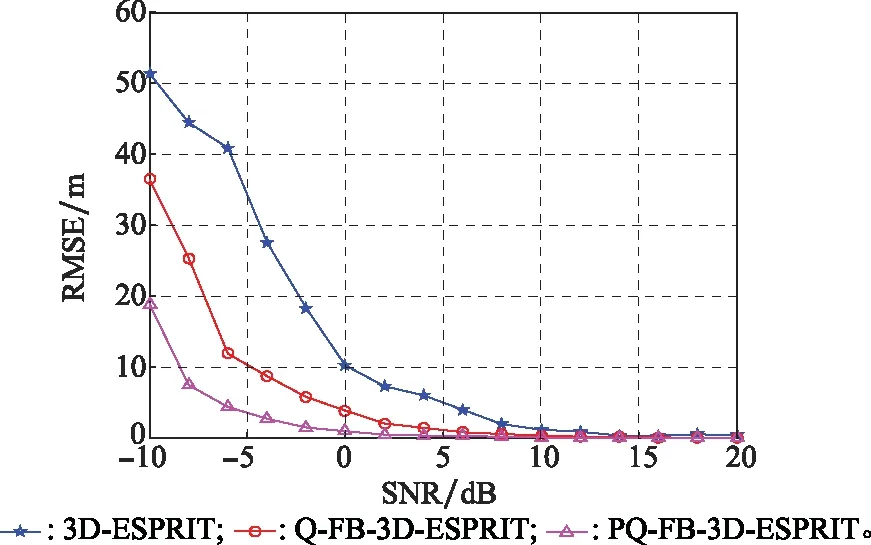
图5 类型参数α的RMSE比较Fig.5 RMSE comparison of type parameter α

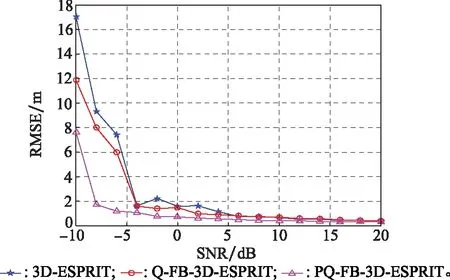
图6 强度参数A的RMSE比较Fig.6 RMSE comparison of intensity parameter A

其中,定义RMSE[20]如下:

(21)

式中,D表示在每一SNR下,进行的蒙特卡罗实验总次数。

由图2～图6可知,相比于经典3D-ESPRIT算法,Q-FB-3D-ESPRIT算法的RMSE要略低,参数估计精度较高,而本文改进算法为3种算法中RMSE最低的算法,具有最高的估计精度,且在低SNR(-10～0 dB)的仿真条件下优势更为明显。同时,SNR增大,3种算法的参数估计精度随之提高并趋于一致。仿真实验验证了本文改进算法的有效性与先进性,即通过对目标极化信息的利用可延长电磁散射数据的可用长度,并有效提高算法的噪声鲁棒性与参数估计性能。

仿真实验 2为进一步验证本文算法的有效性与先进性,在SNR为0 dB及10 dB的仿真条件下,每个SNR对应200次蒙特卡罗实验,分别利用经典3D-ESPRIT算法、Q-FB-3D-ESPRIT算法和本文PQ-FB-3D-ESPRIT算法对4个散射中心位置进行定位并加以比较。

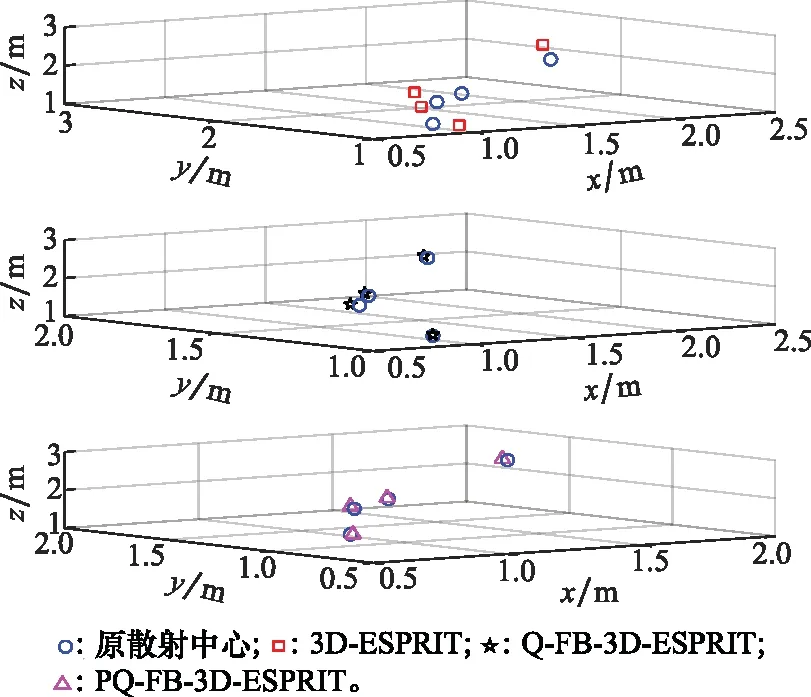
图7 位置参数估计精度比较(SNR=0 dB)Fig.7 Comparison of location parameter estimation accuracy (SNR=0 dB)

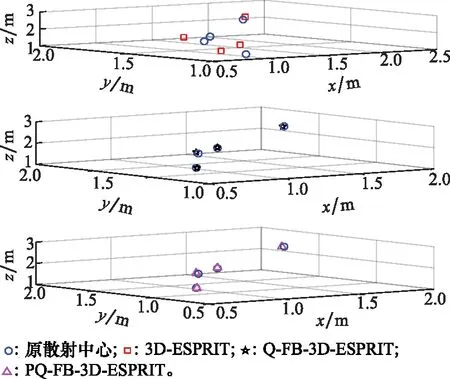
图8 位置参数估计精度比较(SNR=10 dB)Fig.8 Comparison of location parameter estimation accuracy (SNR=10 dB)

由图7可知,在SNR=0 dB条件下,经典3D-ESPRIT算法对4个散射中心均无法准确定位;Q-FB-3D-ESPRIT算法可准确定位其中3个散射中心,而对另一个散射中心的定位则稍有偏差。本文提出的PQ-FB-3D-ESPRIT算法对4个散射中心的位置均能准确定位。由图8可知,在SNR=10 dB条件下,经典3D-ESPRIT算法对散射中心的位置参数估计产生失真;而Q-FB-3D-ESPRIT和PQ-FB-3D-ESPRIT算法均可准确定位4个散射中心的位置。以上两个仿真实验说明,经典3D-ESPRIT算法的参数估计性能与噪声鲁棒性最差,而本文改进算法的参数估计性能与噪声鲁棒性最好,进而验证了本文提出算法的有效性与优越性。

仿真实验 3为验证基于GTD散射中心模型进行目标识别方法的可靠性,设置如下仿真实验。首先,利用FEKO电磁计算软件分别计算3类不同的导弹目标,即目标1、目标2和目标3。其中,入射电磁波频率范围为1～3 GHz,频率步进为0.01 GHz;入射电磁波方位角为0°-180°,角度间隔为1°。因此，每类目标对应的电磁散射数据由300×101维的矩阵构成。进而分别利用支持向量机算法、分类树分类算法及K-最临近算法结合第4节中的目标识别流程进行识别。3类目标在不同算法下的混淆矩阵如图9～图11所示。

图9 基于支持向量机算法分类的3类目标的混淆矩阵Fig.9 Confusion matrices for three kinds of targets classified based on support vector machine algorithm

图10 基于分类树算法分类的3类目标的混淆矩阵Fig.10 Confusion matrices for three kinds of targets classified based on tree classification algorithm

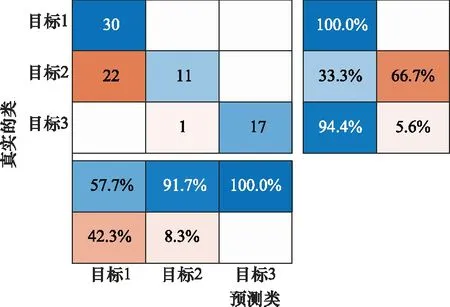
图11 基于K-最临近算法分类的3类目标的混淆矩阵Fig.11 Confusion matrices for three kinds of targets classified based on K-nearest neighbor algorithm

由图9～图11可知,基于支持向量机与GTD散射中心模型对3类目标的识别正确率总体上最好,分别达到了96.6%、90.3%和95.2%;基于分类树算法与GTD散射中心模型结合对目标1和目标2的识别正确率不高;K-最临近算法对目标1的识别正确率达到了100%,而对目标2的识别正确率仅为33.3%。综上所述,基于支持向量机算法与GTD散射中心模型相结合对3类目标识别可达到最优的识别效果。

5 结 语

针对经典3D-ESPRIT算法与Q-FB-3D-ESPRIT算法在估计GTD模型参数时电磁散射数据利用率不足这一问题,本文提出了一种将目标的极化散射信息加以利用的改进PQ-FB-3D-ESPRIT算法。改进算法将极化散射矩阵加入到GTD模型中,增加了模型对极化数据的利用,之后通过前后向平滑、取平方,提高了参数估计精度。

此外,本文还针对基于GTD散射中心模型与智能算法相结合的目标识别方法进行了探究。仿真实验验证了改进算法的先进性与有效性以及基于GTD散射中心模型进行目标识别方法的可行性。本文的研究成果在散射中心模型构建、目标RCS重构拟合、数据压缩等方面具有一定的借鉴意义。