非合作USB测控信号调制指数估计算法

褚梓樾, 王 雪, 赵 航, 商 鹏

(1. 中国科学院国家授时中心, 陕西 西安 710600; 2. 中国科学院大学, 北京 101408;3. 中国科学院精密导航定位与定时技术重点实验室, 陕西 西安 710600)

0 引 言

随着卫星通信、遥感、导航等空间应用需求的不断提升,空间在轨卫星数目急剧增加。为了更好地了解和掌握空间轨道环境,避免卫星碰撞等灾难性事故的发生,需要借助辐射源识别技术对非合作卫星进行侦测和识别[1-3]。辐射源识别是通过发射信号表现出的差异,从复杂的电磁环境中区分出不同目标的。由于辐射源硬件设备固有的不理想特性,发射信号的调制特征参数会产生一定的偏差[4-7](如:正交相移键控信号的正交调制偏差),可将调制特征参数作为细微特征,用于辐射源识别。在轨卫星的正常运行以及与地面站之间的常态信息交互离不开测控系统[8],测控信号作为日常工作信号,其细微特征可作为卫星辐射源识别的稳定特征参数。目前在卫星测控任务中多采用统一S频段(unified S band, USB)测控信号[9-10]。调制指数作为USB测控信号的一个重要参数,决定了信号的功率分配关系[11],即使发射相同信号的辐射源之间也存在功率分配的细微差异。因此，本文将调制指数作为非合作USB测控信号辐射源的一个细微特征,对其进行精确估计。

关于信号调制指数估计的研究,已有的一些方法[12-15]主要针对连续相位调制信号,该类方法均是在连续相位的基础之上建立的,而USB测控信号由于测距码和副载波调制信息的存在,导致信号相位并不连续。其中，文献[13]利用数据辅助的方法来提升算法性能,本文的研究是基于非合作通信,需要对信号进行盲分析,因此这些方法并不适用。文献[16-17]针对角度调制信号的调制指数提出了一种盲估计方法,主要是通过对信号先进行微分再取希尔伯特变换,得到相应的解析形式，对其取模,再根据幅度差异得到调制指数估计值,其研究对象仅具有一个调制指数且基带调制信号形式简单,而USB测控信号具有多个调制指数且基带调制信号往往是多个信号相加复合的形式,利用相应估计算法无法得到各个调制指数的估计值。

因此，本文针对非合作USB测控信号的调制指数,提出了一种基于频域谱分析的估计方法,该方法在低信噪比条件下仍具有较高的估计精度。

1 USB测控信号体制

USB测控体制上/下行信号载频比为221/240,上行信号的载频范围为2 025～2 110 MHz,主要用于传输遥控信号和测距信号。下行信号的载频范围为2 200～2 290 MHz,主要用于传输遥测信号和回传的测距信号。本文利用高增益天线,在地面接收卫星下行信号,因此主要对下行信号进行介绍。

根据文献[10-11]可知,USB测控下行信号的表达式一般为

s(t)=Acos[ωct+β1x1(t)+β2x2(t)]

(1)

式中,A为信号幅度;ωc为载波角频率;x1(t)和x2(t)分别为遥测信号和测距信号;β1和β2分别为遥测信号和测距信号的调制指数。

遥测信号的构成方式一般为脉冲编码调制/相移键控,信号表达式如下:

(2)

测距信号的构成方式一般为伪随机噪声(pseudo-random noise, PRN)序列或单音信号。

(1) 当测距信号为PRN序列时,信号表达式如下:

(3)

(2) 当测距信号为单音信号时,信号表达式如下:

x2(t)=sin(2πfrt)

(4)

式中,fr为单音信号频率。

本文所研究的非合作USB测控信号表达式为

s(t)=Acos[ωct+bc0(t)+mc1(t)sin(Ωt)]

(5)

式中,c0(t)为PRN序列构成的测距信号;c1(t)sin(Ωt)为脉冲编码调制/二进制相移键控方式构成的遥测信号，c1(t)为遥测信息码，Ω为副载波角频率;b和m分别对应测距信号和遥测信号的调制指数。相应的仿真信号频谱如图1所示。通过图1可以看出,该信号频谱特性明显,具有较高的辨识度。其中,标签“1”“8”表示ωc±2Ω处的副载波分量,标签“2”“7”表示调制在ωc±Ω处c0(t)c1(t)的频谱,标签“3”“6”表示调制在ωc±Ω处c1(t)的频谱,标签“4”表示调制在ωc处c0(t)的频谱,标签“5”表示ωc处的载波分量。

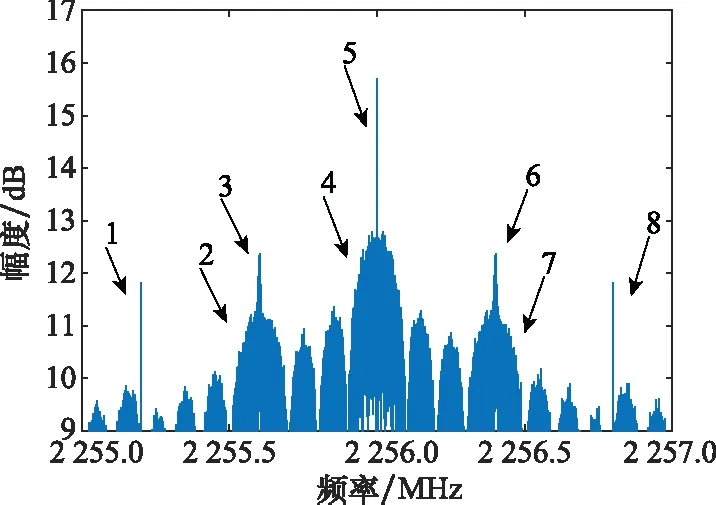
图1 仿真信号频谱Fig.1 Simulation signal spectrum

2 调制指数估计方法

2.1 估计方法理论推导

为了便于理论推导,将式(5)转化为相应的解析信号形式:

s(t)=Aej[ωct+b c0(t)+m c1(t)sin(Ω t)]

(6)

式中,c0(t)和c1(t)为+1或-1,结合贝塞尔函数与三角函数之间的转化的关系:

(7)

(8)

同时根据贝塞尔函数的对称性质J-m(x)=(-1)m·Jm(x),最终s(t)可整理为

s(t)=A[cosb+jc0(t)sinb]·

(9)

对s(t)进行傅里叶变换,可得

F[s(t)]=A[2πδ(ω)cosb+jF[c0(t)]sinb]*

(10)

式中,F[·]表示傅里叶变换;δ(·)表示单位冲激函数；*表示卷积运算。

J2k-1(m)2πδ(ω-(ωc+(2k-1)Ω))*F[c1(t)]]*

(11)

由于图1所示的信号频谱存在明显的冲激谱线特征(标签“1”“5”“8”),所以考虑将冲激谱线的幅度与调制指数之间建立联系。分别取k=0和k=1(或k=-1),可得

(12)

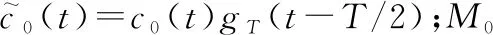
(13)

(14)

将m值代入式(12)中的第一个等式,可得

(15)

为了方便表示,记

则有

(16)

若将m值代入式(12)中的第二个等式,可得

(17)

同理有

(18)

式(16)和式(18)是等价的。

上述求解调制指数过程中所涉及到的非线性函数JP(m)与f(b)对应的函数曲线如图2所示。

图2 非线性函数曲线Fig.2 Nonlinear function curve

该算法基于对信号频谱特征的分析结果,主要的计算量花费在对信号作傅里叶变换,因此该算法的复杂度为O(NlogN),N为信号长度。为了便于更好地理解调制指数的估计过程,图3给出了相应的估计流程。

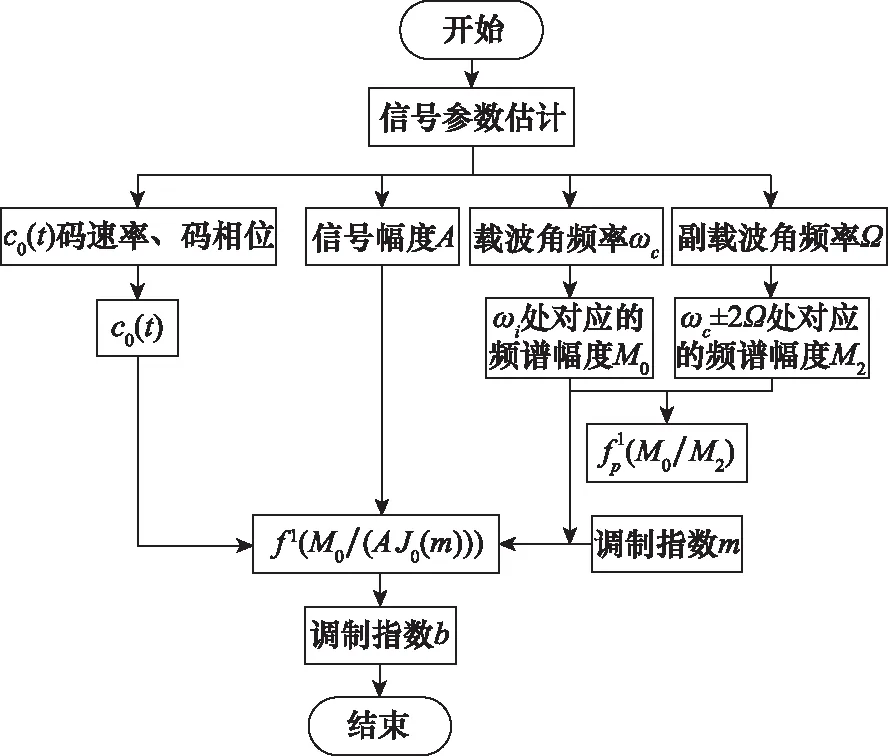
图3 USB测控信号调制指数估计算法流程图Fig.3 Flow chart of modulation index estimation algorithm for USB telemetry tracking and command signal

根据上述理论推导过程以及流程图可知,调制指数估计需要获知一些先验参数,包括:载波角频率ωc，副载波角频率Ω，信号幅度A，c0(t)的码速率和码相位。这些先验参数可分别根据文献[18-21]中的方法得到其精确估计值。

同时,本文算法具有一定的普适性,其核心思想是建立信号频域解析表达式与信号频谱特性之间的联系,构造参数估计方程,通过对方程进行求解,进而得到相应参数的估计值。针对一些其他类型非合作信号的调制指数估计问题(如:文献[16-17]中涉及到的当基带调制信号为单音信号或二进制相移键控信号时的相位调制信号),可对本文信号模型作相应简化与修改,实现具体参数的求解。

2.2 估计误差理论分析

本文提出的调制指数估计方法主要受频谱谱线幅度和信号幅度影响,因此根据文献[22]中的误差传递公式,通过参数估计式(14)对M0和M2及式(16)对M0和A求偏导数以获取估计值的均方根误差,具体表达式如下:

(19)

(20)

式中,

由文献[23]可知:

(21)

(22)

(23)

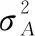
(24)

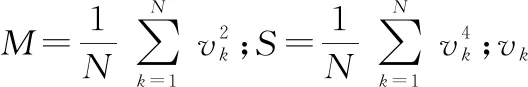
(25)

式中,

(26)

(27)

其中，E(·)为均值；D(·)为方差。根据高阶矩[24]公式:

(28)

式中,σ为噪声标准差,则

(29)

故有

(30)

进而可得

(31)

从式(22)和式(23)可以明显看出,调制指数估计值的均方根误差与信噪比呈负相关,即随着信噪比的增大,均方根误差随之减小。

3 仿真验证

3.1 估计误差仿真分析

根据式(5)利用蒙特卡罗方法在高斯白噪声条件下进行仿真,信号相关仿真参数设置如下:信号幅度A=1,载波频率fc=2 210 MHz,副载波频率f1=4 kHz,调制指数m=0.6，b=0.8,码速率fc0=2 MHz，fc1=1 kHz,码元初始相位均为0 s,采样频率fs=5 MHz,采样时间为1 s。信噪比变化范围为[-10,10]dB,变化步长为2 dB。在每个信噪比条件下仿真Ns=2 000次,若将某信噪比条件下调制指数m的第i次估计值记为mSNR,i,那么在该信噪比条件下估计值的均方根误差可表示为

(32)

式中,m为真实的调制指数。

同理,对于调制指数b有

(33)

式中,b为真实的调制指数。

根据式(32)和式(33)分别给出调制指数m与调制指数b的仿真估计误差随信噪比变化曲线,同时利用在第3.2节得到理论估计误差式(22)和式(23),给出理论估计误差随信噪比变化曲线,并与仿真曲线进行对比。

为了分析调制指数取值对估计误差的影响,利用控制变量法的思想在原有仿真参数的基础上,仅对m和b做相应修改,进行以下两组对照试验:① 保持b=0.8不变,取m=0.4;② 保持m=0.6不变,取b=0.6。将以上两组对照实验得到的估计误差曲线与初始设定参数(m=0.6,b=0.8)对应的估计误差曲线进行对比。以上仿真实验对比结果如图4所示。

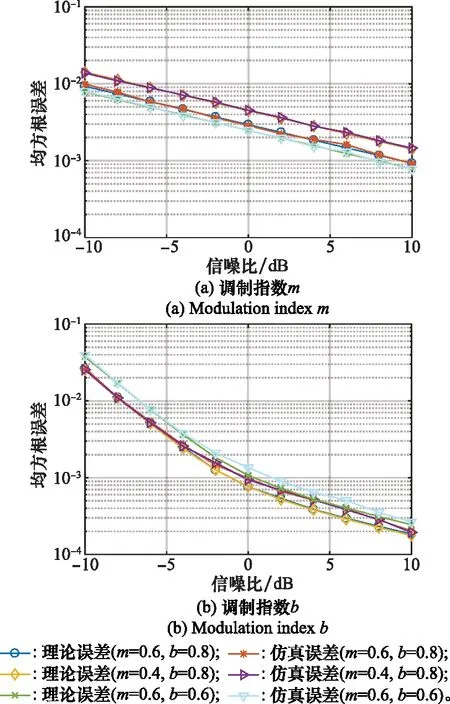
图4 调制指数估计误差随信噪比变化关系Fig.4 Relationship of modulation index estimation error varies with signal to noise ratio

从图4中可以看出,随着信噪比的增加,调制指数的估计误差也随之降低,同时理论估计误差曲线与仿真估计误差曲线也基本一致。通过对比两个调制指数误差曲线可以发现,相同参数条件下在信噪比为-10 dB时,调制指数m的误差小于调制指数b,这是由于m的值仅由信号频谱谱线幅度决定,而b的值除谱线幅度以外还受到信号幅度的影响,信噪比对信号幅度的影响远大于对频谱谱线幅度的影响,当信噪比逐渐增大时,b的估计误差下降趋势明显快于m,当信噪比达到10 dB时,b的估计误差小于m的估计误差。

为便于更清晰地描述对照组实验结果,表1给出了在SNR=10 dB条件下的量化数据对比结果。

表1 估计误差对比结果(SNR=10 dB)

结合图4中的曲线关系与表1中的量化数值可知,当b取值一定时,随着m取值的减小,m的估计误差σm随之增大,而b的估计误差σb则基本保持不变;当m取值一定时,随着b取值的减小,m的估计误差σm也随之减小,而b的估计误差σb则随之增大。根据式(22)和式(23)可知,σm同时受m和b取值的影响,而σb仅受b取值的影响。同时结合图2中的JP(m)和f(b)函数曲线可知,m与JP(m)呈反比例关系,b与f(b)呈反比例关系,而σm与JP(m)呈正比关系与f(b)呈反比关系,σb与f(b)呈正比关系。因此,σm与m呈反比例关系,与b呈正比例关系;σb与b呈反比例关系。上述仿真结果与理论分析结果保持一致。

3.2 实测信号对比验证

本文采用的实测信号是在中国科学院国家授时中心西安场区,利用13 m高增益天线采集到的某颗低轨卫星发出的USB测控信号,实测信号数据采样频率为250 MHz,采样时长为2 s。取3组等长且不同时段的实测信号数据,按照图3所示的流程得到调制指数的估计值,同时其他参数的估计结果如表2所示。

表2 实测信号参数估计值

为了验证本文提出的调制指数估计方法的准确性,利用上述参数估计值生成恢复信号,并与相应的实测信号从频域和时域两方面进行对比。观察以上3组参数估计值,除了由时间段选取所导致的码相位不同以外,其余参数估计值的差异较小,在此选用第1组估计值进行对比验证。

3.2.1 频域对比

根据USB测控信号频域式(10)可知,信号频谱幅度受调制指数的影响,因此通过对比实测信号与恢复信号频谱幅度的差异可以判断调制指数估计算法的准确性。相应的信号频谱对比结果如图5所示。

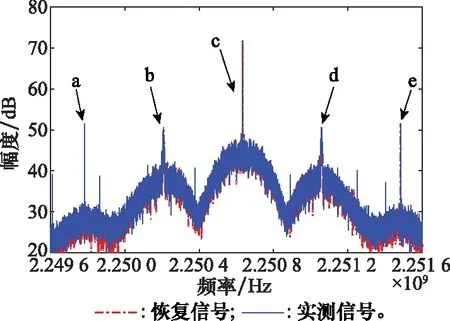
图5 实测信号与恢复信号频谱对比Fig.5 Spectrum comparison between measured signal and recovered signal

为了更好地展示实测信号与恢复信号的频谱对比结果,下面将标签a～标签e进行适当放大,此外还将标签b和标签d进行了平滑处理,结果如图6所示。

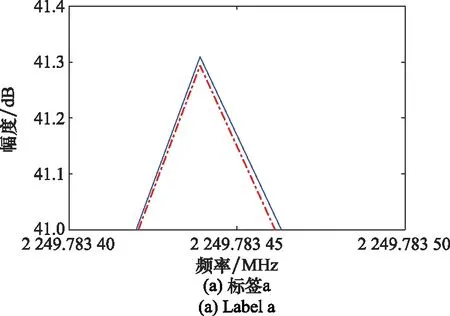
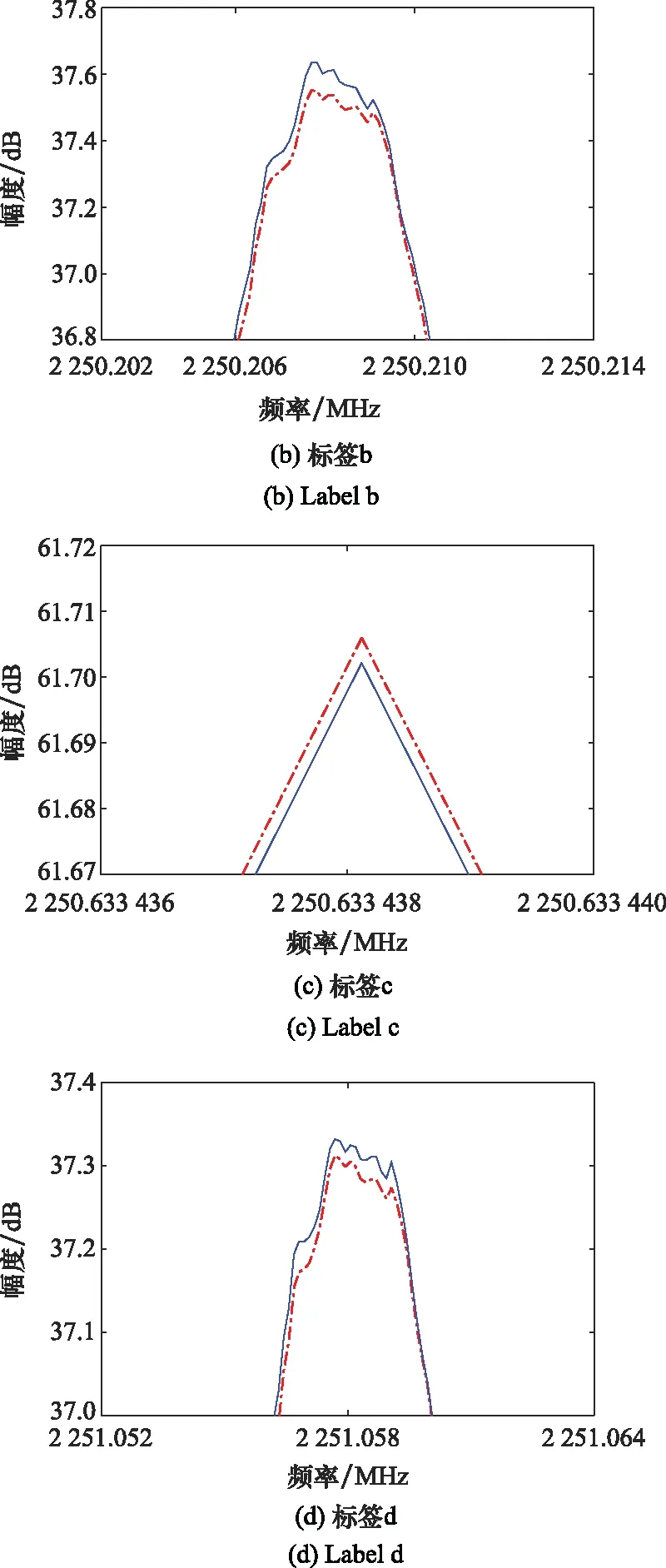
图6 经放大和平滑处理后标签a～标签e对比结果Fig.6 Comparison results of labels a～e after amplification and smoothing

根据式(12)可知,标签a，标签c，标签e的频谱幅度主要由调制指数决定,结合上述对比结果,可以看出恢复信号和实测信号的频谱幅度基本一致。其中，标签a、标签b、标签d对应的实测信号频谱幅度大于恢复信号频谱幅度,而标签c和标签e对应的实测信号频谱幅度小于恢复信号频谱幅度,并且经过平滑处理后的标签b和标签d中恢复信号频谱与实测信号频谱的波动性存在些许差别。这些现象产生的原因是，在利用高增益天线采集卫星信号的过程中,采集到的信号中不仅包含噪声,还包含许多干扰信号,而采集设备的采样率有限,会导致一定的频谱混叠现象,将一些干扰信号的频谱混叠进来,这些干扰信号会对实测信号的频谱幅值产生影响,而恢复信号中不包含干扰信号,因此不会产生频谱混叠的问题。通过计算相应点幅度差,可以得到标签c对应的频谱幅值误差小于0.01 dB,标签a、标签b、标签d和标签e对应的频谱幅值误差小于0.08 dB,表明利用本文提出的估计算法得到的调制指数较为准确。

3.2.2 时域对比

若求整体时域基带信号,通过式(6)可知,调制指数m和b包含在基带信号的相位中,无法直观地进行对比,利用幅度受调制指数决定的基带信号进行对比则更为直观。结合USB测控信号时域式(9)与图5所示的信号频谱图,记图5中标签c对应的基带信号为sbase1,b对应的基带信号为sbase2,标签a对应的基带信号为sbase3。以上3个基带信号的近似表达式为

(34)

式(34)直观地体现出调制指数对基带信号幅度的影响。标签d对应基带信号与标签b的仅相差一个负号;标签e对应基带信号与标签a的相同。此外由于标签a和标签e的能量较低,通过解调无法得到较好的基带波形,且sbase1和sbase3呈倍数关系,因此只需对比标签b和标签c对应的实测与恢复基带信号幅度,即可验证调制指数估计的准确性。相应的实测与恢复基带信号对比如图7所示。

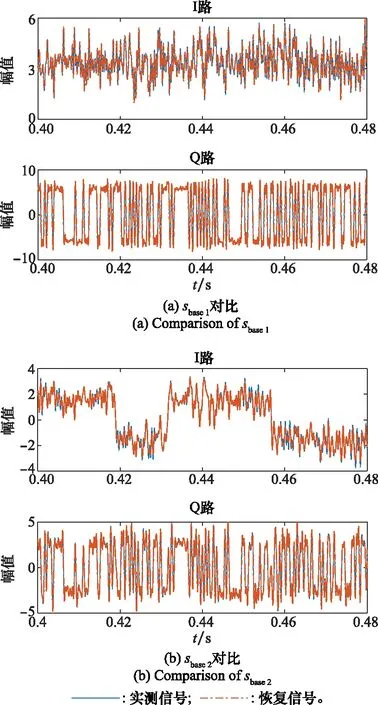
图7 实测信号与恢复信号的基带信号对比Fig.7 Comparison of baseband signal between measured signal and recovered signal

根据基带信号的对比结果以及式(34),sbase1的I路在理想情况下应为常数,但却出现波动现象,并且Q路在码片持续时间内也具有波动性。sbase2的I、Q两路也存在类似情况,这均是由于信号频谱相邻成分的旁瓣导致的。sbase1对应的实测信号与恢复信号一致性较好,sbase2对应的实测信号与恢复信号波动性存在些许差异。这是因为标签c信号频谱能量较高,不易受噪声干扰,且实测信号频谱处基本不存在干扰信号,而标签b相对标签c能量较低,且实测信号频谱存在干扰信号。总体上,sbase1和sbase2对应的实测信号与恢复信号幅度基本一致,即验证了调制指数估计的准确性。

为了量化时域对比结果,引入归一化互相关函数[25]的概念。通过计算实测基带信号与恢复基带信号的归一化互相关函数最大值,若该值越接近于1,说明实测基带信号与恢复基带信号的一致性越高。归一化互相关函数计算公式如下:

(35)

式中，sreal(t)表示实测基带信号;sreco(t)表示恢复基带信号;(·)*表示共轭。

利用式(35)分别计算sbase1和sbase2对应实测信号与恢复信号的归一化互相关函数最大值,在表3中列出了相应的计算结果。

表3 基带信号归一化互相关函数最大值

上述结果表明，sbase1和sbase2对应的实测信号与恢复信号的归一化互相关函数最大值均接近于1,即实测基带信号与恢复基带信号一致性较高,能够说明调制指数估计得较为准确。

4 结 论

本文针对非合作USB测控信号的调制指数,提出了基于频域谱分析的估计方法。首先根据信号频谱的谱线特性,由信号频域表达式推导出调制指数估计方法,并对该方法的估计误差进行了理论分析。通过蒙特卡罗仿真得到调制指数估计误差随信噪比变化关系曲线,同时将理论估计误差曲线与仿真估计误差曲线进行对比,验证了理论分析的正确性。并仿真分析了在不同调制指数取值的条件下,调制指数估计误差的变化情况。在此基础上,利用实测低轨卫星信号数据对调制指数估计方法进行了验证,根据估计参数生成恢复信号,从频域和时域两个方面与实测信号进行对比。通过信号频谱幅度、时域基带信号波形及其归一化互相关函数最大值的对比结果表明，实测信号与恢复信号的频谱幅度误差较小、时域基带信号波形的一致性较高、归一化互相关函数最大值接近于1。进一步说明本文提出的调制指数估计方法精度较高,可为非合作卫星辐射源识别提供高精度的参数支撑。