基于ARIMA乘积季节模型的科室级常规耗材需求量预测研究

白玲，郭晓伟，马莉

首都医科大学附属北京友谊医院 采购中心，北京 100050

引言

相比于高值介入耗材的“寄售制、零库存、先使用后结算”的全程可追溯管理方式，常规医用耗材管理方式较为粗放，存在科室覆盖广、种类繁多、需求量大，科室须持有一定数量的库存以保证正常诊疗等特点[1-3]，且医院以领用量为结算依据。因此库存积压、频繁采购势必增加医院的资金投入。

随着医药体制改革政策的不断出台，不少大型医院已建立较为完善的物流信息管理系统，实现了医院耗材从规范化管理转向精细化管理，科室级管理将常规一次性耗材的管理从原有的“以领代消”转变为“实用实消”的模式[4-6]。在精细化耗材管理进程中，采购订货是其中一个不可忽视的环节[7-8]。制定科学的采购需求，设置安全库存量，在保证临床诊疗的正常进行、维持医院的供需平衡的基础上，可有效减少库存成本，避免资源浪费，进而使医院资金效益最大化[9]。

医院耗材采购需求多根据经验进行，或大致设置一个基数，如将采购量设为15天平均消耗量-实时库存[10]，但15天消耗量如何设定未深入介绍。目前已有一些研究学者提出使用预测模型进行采购需求预测，张美艳[11]利用多种预测模型组合方法进行预测，该类方法通过对不同的预测模型按比例线性组合，但其中有预测模型贡献率较低，且方法较为复杂，应用的可行性还需探讨。许亮业等[12]基于整合移动平均自回归（Autoregressive Integrated Moving Average，ARIMA）模型进行全院医用低值耗材需求量预测，该模型已广泛应用于卫生领域预测中，认为具有良好的预测效果。由于医用耗材的使用依赖于医院门诊量和住院病人数量，研究中未考虑季节性、周期性因素。王志强等[13]利用ARIMA模型预测了某科室非医用低值耗材的采购金额，模型残差序列为白噪声，信息提取完整，说明该类耗材不含季节性因素。该研究数据为领用金额，未考虑调价对金额的影响，且领用非实际使用，可能影响预测模型的准确性。

获取使用量而非领用量对于模型预测的准确性至关重要。本研究选取的医院已建立科室基础耗材库，实现了实用实消的精细化管理模式。本文将建立基于时间序列分析法的采购预测模型，并考虑季节性因素影响，预测未来周期的采购需求量，减少库存成本，提高资金投入的利用率。

1 材料

本研究中的数据选自北京某医院某内科病房的5 mL一次性使用注射器2014年1月至2018年12月的逐月实际使用量，用于构建预测模型，选取2019年1月至6月的实际使用量用于模型验证。

2 研究方法

本研究采用EViews 10.0软件通过季节性差分自回归滑动平均（Seasonal Autoregressive Integrated Moving Average，SARIMA）模型对采购需求量进行预测。SARIMA模型构建的流程为：构建时间序列、平稳性检验、白噪声检验、ARIMA模型选择及定阶、模型检验、模型应用。

对获取的时间序列进行平稳性检验，方法主要有两种：① 通过序列自相关和偏相关图判断，若序列相关图随机分布在0周围，视为平稳；② 依据单位根检验进行判断，若检验P＜0.05，说明序列平稳，否则序列不平稳。对于不平稳的序列需要进行数据处理，通过差分过程使时间序列平稳化。

对观测序列进行白噪声检验，用以判断序列是否具有随机性。若序列涵盖了季节等因素时，应选取季节乘积ARIMA模型，即ARIMA（p,d,q）（P,D,Q）s，并根据差分次数和自相关与偏自相关图进行参数的确定。利用AIC准则或BIC信息准则法确定最优模型。对预测模型残差还需进行Q检验，以确保模型信息提取完整。

对构建的模型进行回代拟合，与实际值进行误差和残差检验，若误差在合理范围内，且残差序列为白噪声，说明信息提取完整，模型拟合效果好。

3 模型构建

3.1 序列平稳化

通过观察图1可知，该序列在每年2月、10月都有一个低峰，序列底部有抬高趋势，呈现一定周期性，应与节假日及前后就诊人数呈正相关。通过时间序列的自相关和偏自相关图（图2）也可看出，序列并未趋近于0，说明序列不平稳。

因观测序列含有一定的周期性，需对序列进行非季节性和季节性差分各一次，季节性差分周期为12，差分后自相关和偏自相关图如图3所示。可见序列基本在置信区间内0附近，序列基本平稳，通过单位根检验，得到观测序列的P值为0.3682，差分后序列的P值为0，P＜0.05，同样说明序列平稳。

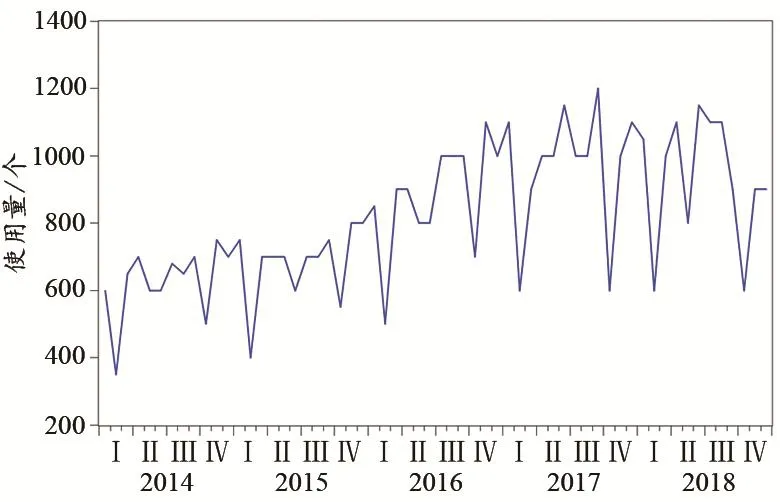
图1 使用量观测序列时序图

图2 观测序列的自相关图和偏自相关图

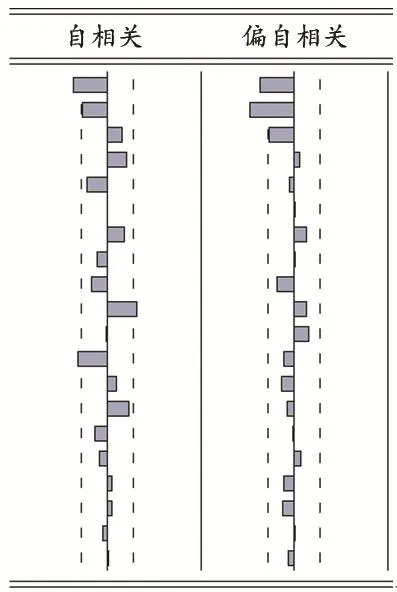
图3 经过季节性和非季节性差分的序列自相关图和偏自相关图

3.2 白噪声检验

对差分后序列进行Box-Ljung Q统计量检验，P＜0.05，说明序列为非白噪声序列，序列中有可提取的有价值信息。

3.3 模型选取与定阶

本研究首先尝试使用不考虑季节性因素的ARIMA模型进行预测，对其残差序列进行Q检验，检测有效信息提取的完整性，如图4所示。12阶后，P＜0.05，说明残差序列不全是白噪声，信息提取不完整。

众多研究成果表明，医院就诊、住院人数与季节相关[14-15]，而常规医用耗材使用量又依赖于患者数量，在构建预测模型时，应充分考虑季节性因素，因此模型选择季节性乘积模型，即ARIMA（p,d,q）（P,D,Q）s。原观测序列进行非季节性和季节性差分各一次，因此d=D=1，s为12。差分后时间序列的自相关图与偏自相关图从严格意义上均拖尾。本研究通过AIC信息准则进行验证，其中自相关图一阶后进入置信区间，q选在（0,2）范围内，偏自相关图两阶后进入置信区间内，因此p初步选在（0,3）范围内，自相关图第12阶未落入置信区间内，Q为1，偏自相关图12阶落入置信区间内，P选为0。通过AIC最小准则，经过多次拟合，ARIMA（0,1,2）（0,1,1）12模型AIC最小，为12.488，其预测效果见图5。提取残差序列进行Q检验，如图6所示，P＞0.05，残差序列为白噪声，说明信息提取完整，模型可靠。因此，最终模型构建结果为ARIMA（0,1,2）（0,1,1）12。

图4 非季节性ARIMA模型残差序列Q检验结果

图5 实际使用量与预测用量对比图

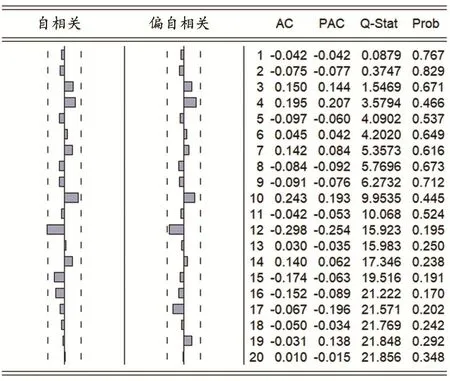
图6 ARIMA季节乘积模型残差序列Q检验结果

3.4 模型应用

以2019年1至6月的该品牌5 mL一次性使用注射器的实际用量作为验证集，将预测值与验证集进行对比分析，结果如表1所示。预测模型的平均绝对百分比误差MAPE=5.308，在可接受范围内，说明预测效果良好。

表1 2019年1至6月实际使用量与预测量比较（个）

本研究将该预测模型应用于同品牌其他两种规格（10 mL和30 mL）的注射器中，平均绝对百分比误差MAPE分别为6.950和6.457，同样在误差可接受范围内。

4 讨论

综上所述，构建预测模型时应考虑季节性因素影响，还需对预测结果进行相关检验，保证提取全部有效信息。

模型预测数据不建议使用采购量或采购金额，前者不是实际用量有可能影响预测结果，后者同时增加了调价对预测结果准确性的影响。在全院范围内建立科室常规耗材库，使科室耗材实现“实用实消”，对构建预测模型提供了重要的管理构架上的保证。为便于盘点等相关工作的顺利进行，现阶段该医院对科室常规耗材库的要求为按采购最小包装出库，如本研究中的5 mL注射器采购最小包装数量为50个/盒，因此根据预测结果可采用四舍五入法或向上取整法进行采购。今后实现常规耗材条码化管理后，出库会趋于精细化，对于采购需求的预测也将会更加准确。

后续研究还需验证该模型对其它品牌、种类耗材的适用性，检测是否需要针对不同耗材个性化建模，并探索批量处理手段和方法，最终实现科室、全院范围的推广。

5 结论

本文通过ARIMA季节乘积模型预测了未来一段时间某类耗材的使用数量，取得了较理想的成果，并讨论了季节性因素对常规医用耗材预测模型的影响。今后可逐步扩展品规、科室至全院范围。本项研究可用于基于物流信息系统的科室、全院支出预算控制，提高支出预算制定的精细化程度。同时，也可对减少库存成本，提高经济效益提供帮助。