基于加权水平集演变算法的医学图像分割研究

魏应敏，王薇，张媛

南京医科大学附属南京医院（南京市第一医院）放射科，江苏 南京 210006

引言

图像分割是指根据灰度、颜色、纹理和形状等特征把图像划分成若干互不交迭区域，使同一区域内呈现特征相似性，而不同区域间呈现显著差异性[1-3]。图像分割能提取出目标区域有用信息，可应用于模式识别、计算机辅助诊断和3D可视化等方面。图像分割算法主要分为阈值法、边缘检测、区域增长和基于特定理论等[4]。本研究着重探讨水平集活动轮廓模型，可理解为一个平面上的曲线表示成一个二元函数的零点集合，即将图像分割问题转化为一个能量泛函极小值问题，然后此时偏微分方程的极小解即为图像分割结果，逐步将零水平集曲线驱使到目标区域边界。目前水平集算法主要有基于区域信息、形态优先模型和基于相位信息等[5]，但是各算法均对图像灰度不均、边界模糊和初始轮廓位置较为敏感，难以在目标区域边界附近收敛[6-7]。本研究采用局部边缘强度和局部边缘方向作为图像特征构造图像能量函数，客服水平集算法固有缺陷，其中局部边缘方向采用图像梯度向量流场检测，且引入加权函数重构图像目标能量函数中区域项和长度项，控制能量函数在边界模糊区域溢出。

1 方法

1.1 传统的水平集算法

假设有一个表面S，它与一个平面P相交，得到一个曲线C，此轮廓C即为通过水平集算法能量函数演变得到的图像目标区域边界[8]。当采用水平集算法进行医学图像分割时，图像灰度、边缘或纹理均可被用来定义目标函数。本研究采用图像边缘信息作为图像主要特征驱使初始轮廓达到理想边界，图像边缘强度见公式(1)[9]，其中g∈[0,1]，I是在Ω维度上的图像，Gσ是标准差为σ的高斯核函数，*表示卷积运算。

基于边缘强度函数g可构建水平集算法的基本能量函数，由公式(2)给出，其中R(φ)是距离调节项，由于水平集函数在零点过于平坦或者陡峭，影响算法稳定性，可用R(φ)保持水平集函数的理想形状[10]。Length(φ)是能量函数长度项，代表活动轮廓C长度，见公式(3)，当目标轮廓处于零水平集时，Length(φ)取得最小值。Area(φ)是能量函数区域项，代表活动轮廓C内部区域，控制零水平集的活动演变速度。区域边界平滑时，加速演变，反之减缓演变速度，见公式(4)，其中H为单位阶跃函数。当图像为区域光滑、边界显著时，公式(2)能量函数最小值即可提供优越的图像轮廓。

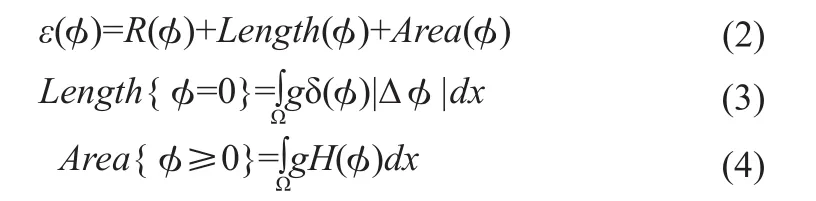
1.2 提升的水平集算法

然而，医学图像常常是灰度不均、边界模糊，传统水平集算法进行轮廓演变时难以准确探测图像边界[11-13]。本研究着重提升水平集算法图像边界探测准确性，加入基于轮廓C内外轮廓的邻域特征加权函数ω，构建新的能量函数长度项和区域项，所用特征包括平均边缘强度和图像梯度向量流场方向与图像轮廓C移动方向的平均差异γ，见公式(5)～(7)，式中k是常数，决定轮廓C邻近边缘特征数。轮廓C邻近的轮廓演变由公式(8)给出，其中m属于整数，正负代表轮廓位于轮廓C的内外侧，使得轮廓演变从零水平集沿着法线方向扩展，演变过程见图1a。∈[0,1]是轮廓C邻近2k条轮廓边缘指示器的平均强度，见公式(9)。图像梯度向量流场方向能预测边缘方向扩展走向，基于此可计算出轮廓C的法向量和2k条梯度向量流场临近轮廓线内积，γ∈[-1,1]，法向量见公式(10)，其中表示图像梯度向量流场，由图1b所示。

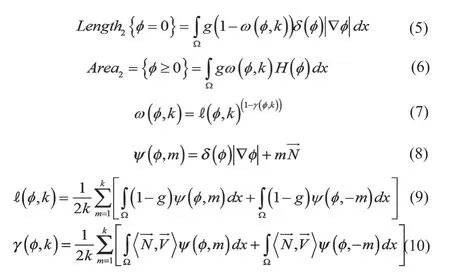
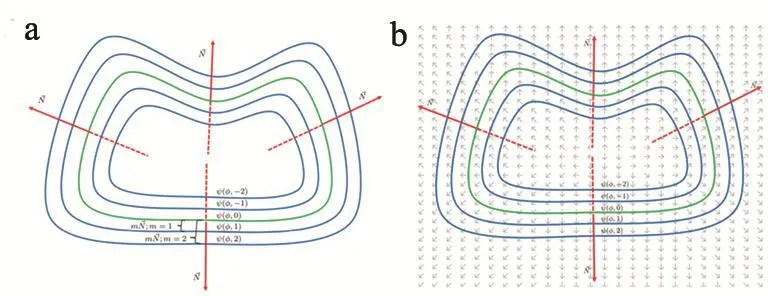
图1 提升的水平集算法示意图

将公式(5)和(6)带入公式(2)可得新的能量函数，见公式(11)，其中μ是大于0的常数，p是|Δφ |=1时，距离调节项R取最小值的能量密度函数，通过求解梯度函数公式(12)可获得公式(13)能量函数的最小值，即可得图像目标最佳边界。其中dp为p函数的一阶导数，加权函数w根据局部边缘特征分配不同优先级到长度项和区域项，特征为边缘强度和梯度向量流场与活动轮廓C法向量的线性度γ，图2为不同和γ对应的加权函数曲线，可见不管γ取值，当为1时，w趋近于0，即当零水平集位于图像非光滑区域时，长度项占目标边界的主要能量。反之，区域项占主导地位。当γ趋向-1，随着增长，w下降缓慢，表明轮廓C移动的法向量与梯度向量流场方向相反，此时长度项成为主要能量，保证轮廓C维持目标边界形态。同时，加权函数允许轮廓C在相对平滑区域内变形，即使此时移动的法向量方向与轮廓C周围梯度向量流场方向相反，这非常有利于初始轮廓线被设定远离最佳轮廓时，甚至在灰度不均情况下。

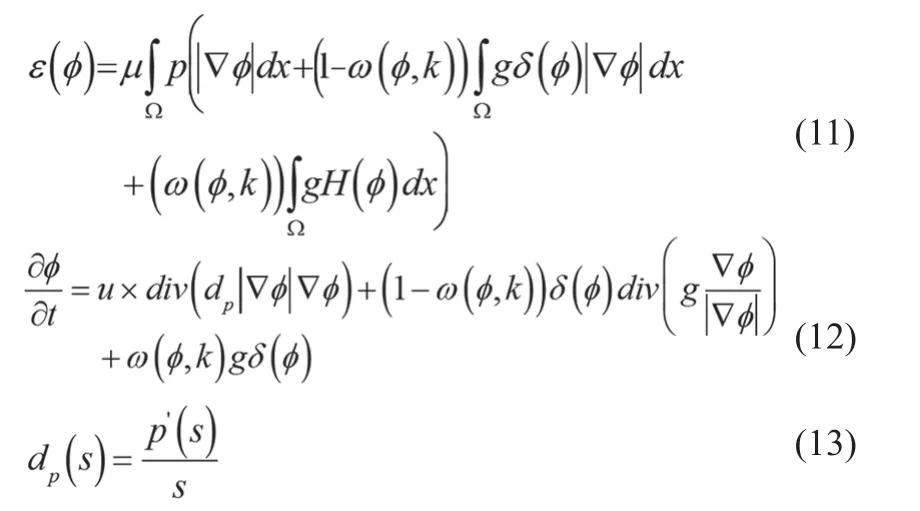
1.3 图像分割结果评价

本研究采用定性与定量相结合评估分割图像质量，定性分析主要基于视觉效果，定量评价采用Dice相似性系数（Dice similarity coeffi cient，DSC）[14-15]，公式见 (14)，其中A和B代表分割所得区域和真实区域，采用专家手工分割结果作为真实区域，∩表示交集，∪表示并集，DSC处于[0,1]，值越大表示算法分割性能越佳。

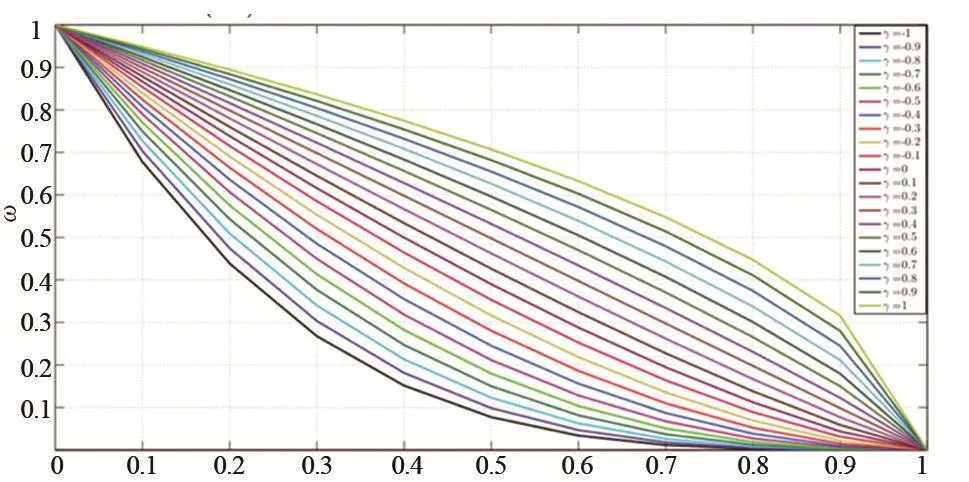
图2 不同和γ对应的加权函数w

2 结果与分析

选用临床实例图像进行仿真实验，并将本研究提出的分割算法与现存的水平集分割算法如相变算法（Reaction Diff usion，RD）[16-17]、 水平集扩散算法（Level Set Diff usion，LSD）[18-19]和距离调节水平集演变算法（Distance Regularized Level Set Evolution，DRLSE）[20-21]等进行性能比较。所有算法测试均在Matlab2013a编程环境下实现。各算法参数设置见表1，其中μ、α和λ都是常数，决定各算法中调整项、区域项、距离项的影响。

表1 不同水平集算法参数设置

2.1 临床实例图像分割

30例临床实例包括图像1～15为脊柱MR，图像16为脑部MR，图像17和18代表骨盆MRI，图像19和20代表颅骨CT，图像21～28代表腰椎MR，图像灰度差异小且边界不均，加大了分割难度。临床图像按迭代次数做两次图像分割，第一次迭代次数取本研究提出算法收敛次数（图1～18和27迭代50次，图19～20迭代100次，图21～25和29～30迭代60次，图26迭代70次），第二次迭代次数均较第一次增加多次（图1，21-25和27迭代80次，图2～3，5～18和 29～30迭代 100次，图 19～20迭代 140次，图 26迭代90次，图28迭代130次）。

各算法图像分割结果见图3～4。视觉分析可知，第一次迭代的图像分割结果中，基于本研究分割算法获得的目标轮廓与真实边界吻合度最高。实验19和实验21图像目标与周围区域对比度差异小，且边界清晰度弱，但是基于本研究算法依然能准确分割出目标区域，其他算法分割所得目标轮廓均与真实边界差异较大，属于分割失败。即使ED和DRLSE算法能分割出实验1图像准确的目标边界，但是当增加迭代次数时，目标边界偏离真实边界较大，表明算法不稳定。对于挑战性较大的实验27和实验28，基于本研究算法准确的分割出盲肠目标区域，且其他算法均不能准确分割出骶骨目标。第二次迭代所得图像分割结果显示，增加迭代次数，其他三种算法分割所得目标轮廓脱离真实目标边界程度更大，表明算法不稳定性加大。而基于本研究算法分割所得目标边界变化微弱，表明本研究算法较强的鲁棒性，这主要由于边缘信息和演变轮廓内外侧区域的梯度向量流场方向能控制不同能量项的影响。

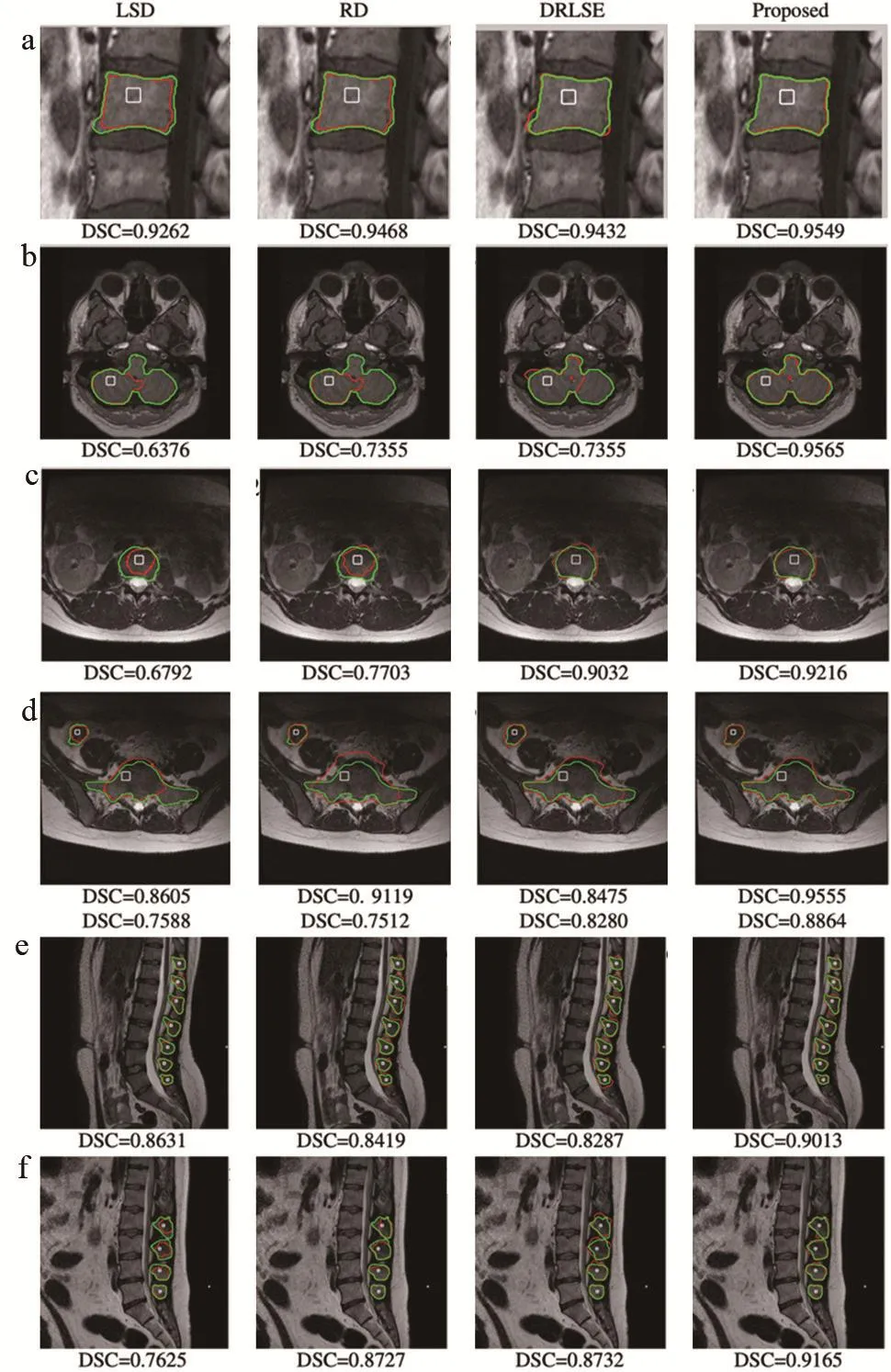
图3 不同算法第一次迭代所得图像分割结果

各算法图像分割定量分析结果，见图5。可以看出基于本研究算法绝大多数实验图像分割所得DSC结果均优于其他三种算法。在第一次迭代的实验2、14～17中和第二次迭代的实验11、13、15、17中，其他算法DSC值略高于本研究算法。对于第一次迭代的实验2图像，RD算法没有收敛，且在第二次增加迭代次数时DSC值降低。对于第一次迭代的实验14～17图像，DRLSE算法获得最高的DSC值，但当增加迭代次数，基于本研究算法可获得实验14和16图像最高的DSC值，表明本研究算法需要更多迭代次数才能获得理想的目标边界。对于第二次迭代的实验15和17图像，DRLSE算法所得DSC值较本研究算法仅提升0.67%。对于第二次迭代的实验11和13图像，RD算法较本研究算法提升0.004%。对于第二次迭代的实验2～4，RD算法和LSD算法同样由于迭代次数增加导致结果溢出，DSC值下降，分割性能下降。对于实验21～28图像，本研究算法较其他算法更快收敛，且获得更高的DSC值。对于实验29和30图像，目标边界相当薄弱，其他三种算法在第一次迭代中未能收敛，第二次迭代时结果出现溢出。

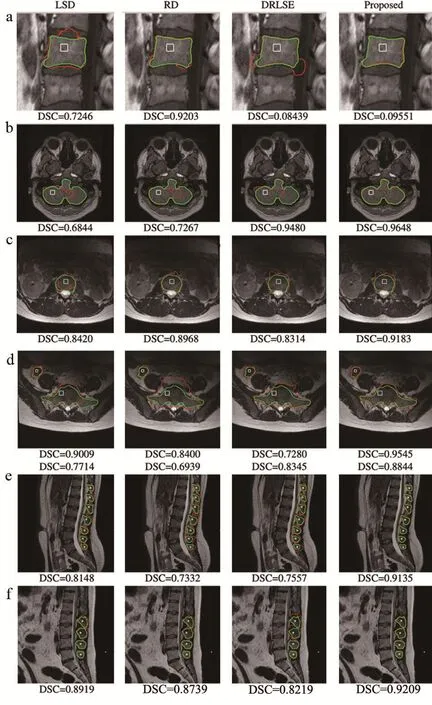
图4 不同算法第二次迭代所得图像分割结果

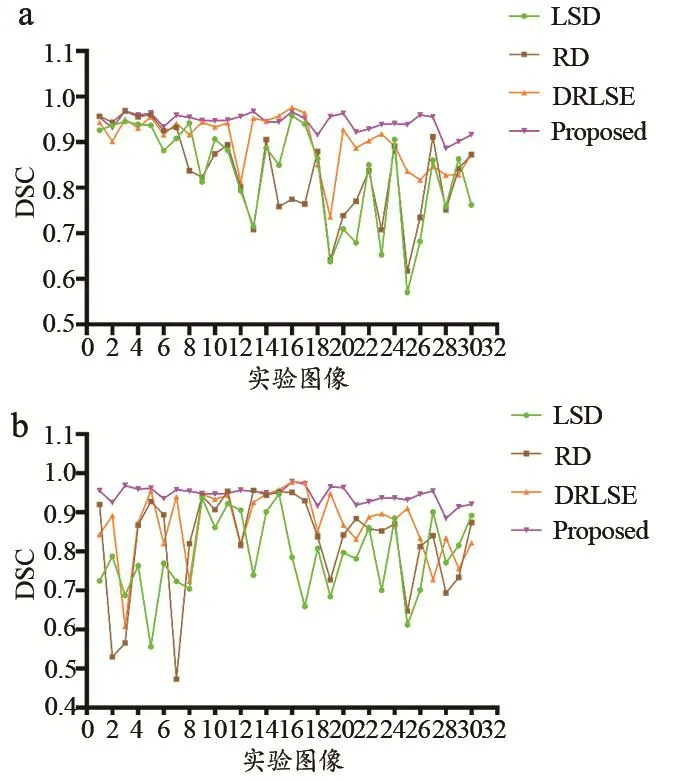
图5 不同算法两次迭代所得DSC值

2.2 不同初始轮廓位置的影响

为了测试不同分割算法对初识轮廓位置的敏感度，采用实验1图像进行测试，结果见图6。可以看出RD算法优于LSD算法和DRLSE算法，能较准确提取目标边界。当初始轮廓位置位于目标区域边界薄弱地带时，LSD算法不能提取出目标边界。基于本研究算法图像分割视觉效果因初始轮廓位置不同无差异，且DSC值变化微弱，表明本研究算法的稳定性和加权函数w根据局部特征可控制能量变化的影响。

图6 不同初始轮廓位置对不同分割算法的影响

3 结论

本研究提出一种新颖的水平集活动轮廓模型，主要基于局部边缘特征构造加权系数控制目标能量函数。具体为将边缘强度信息与演变轮廓邻域内外边缘方向信息结合在一起，这些图像信息用于决定能量函数中不同能量项的重要性。使得本研究算法能够准确驱使初始轮廓演变到目标理想边界，即使目标边界模糊情况下也能表现优越。实验表明，本研究算法收敛较其他水平集算法需更低的迭代次数，获得更高的Dice相似性系数，更优越的分割性能。