波形钢腹板组合箱梁扭转简化计算与设计
2021-01-25张江峰沈孔健
张江峰, 沈孔健
(1.中交公路规划设计院有限公司, 北京 100088; 2.东南大学, 江苏 南京 210096; 3.江苏省交通工程建设局, 江苏 南京 210004)
0 引言
波形钢腹板组合箱梁以其独特的优势,如自重轻、外形美观、无腹板开裂问题、施工效率高等,逐渐在桥梁工程中得到应用。但是波形钢腹板组合箱梁的抗扭刚度较传统混凝土箱梁低,其扭转效应也得到了越来越多的关注。
近年来,波形钢腹板组合箱梁纯扭转全过程的力学响应分析理论得到了较大的发展,MO[1]等将适用于混凝土梁扭转构件的变角软化桁架模型扩展到波形钢腹板组合箱梁纯扭转全过程分析中,并基于此模型提出了相应的设计方法;在此基础上,聂建国[2]、KO[3]、ZHU[4]等采用不同的剪截面剪应变关系,提出了改进模型;丁勇[5]等将适用于混凝土构件的固定角软化桁架模型扩展到波形钢腹板组合箱梁纯扭转全过程分析中,并基于规范进行了抗扭设计验算;SHEN[6]等和ZHOU[7]等将适用于混凝土构件的软化薄膜模型扩展到波形钢腹板组合箱梁纯扭转全过程分析中,可较好地预测预应力混凝土波形钢腹板组合箱梁扭转力学性能。
虽然全过程分析模型可较完整地预测结构扭转性能,但过程繁琐,需编程进行计算;在结构扭转分析中,最关心的是混凝土开裂、波形钢腹板屈服、钢筋屈服破坏等关键状态下的结构响应。因此,通过计算关键状态下的结构响应,如开裂扭矩、屈服扭矩、极限扭矩及相应阶段的扭转刚度,即可快速确定结构扭矩和扭率宏观力学响应。同时,可基于关键状态下的扭矩计算公式,提出波形钢腹板组合箱梁的设计方法。鉴于此,本文对波形钢腹板组合箱梁扭转过程关键状态下的扭矩和扭转刚度进行研究,得到结构在外加扭矩作用下的扭矩扭率简化曲线,并提出相应的设计方法,为进一步完善波形钢腹板组合箱梁扭转计算理论和结构设计提供借鉴。
1 波形钢腹板组合箱梁纯扭转简化计算
波形钢腹板组合箱梁满足正常设计条件时,波形钢腹板组合箱梁在纯扭矩作用下,荷载从零加载到极限扭矩Tu过程中,扭矩扭率曲线可简化为图1中的三段式直线。在弹性扭转阶段,结构承受的扭矩T与扭率θ成线性关系,弹性扭转刚度为K0;当扭矩达到开裂扭矩Tcr后,混凝土发生开裂,刚度将发生折减,当忽略开裂混凝土的贡献时,组合箱梁钢筋和波形钢腹板仍处于弹性阶段,扭转刚度为KⅠ;当扭矩达到屈服扭矩Ty时,波形钢腹板发生屈服;此后,波形钢腹板承担的扭矩基本不变,而钢筋将发挥较大作用,扭转刚度可简化KⅡ。当混凝土顶底板钢筋屈服时,结构达到极限承载力Tu。显然,若计算得到结构扭转刚度及关键点处的扭矩,即可得到结构的扭率,获得结构在扭转全过程的扭矩扭率曲线。

图1 波形钢腹板组合箱梁扭矩扭率关系Figure 1 Torque and twist relation of composite box girder with corrugated steel webs
1.1 混凝土开裂前弹性扭转刚度
沈孔健[8]等将波形钢腹板与混凝土组合截面换算成全混凝土截面,基于扭转试验值拟合得到弹性阶段扭转刚度K0的修正公式:
(1)

图2 波形钢腹板混凝土组合箱梁结构示意图Figure 2 Structural schematic diagram of concrete composite box girder with corrugated steel webs
由于波形钢腹板混凝土组合箱梁的扭转刚度是由混凝土板和波形钢腹板贡献的,则式(1)也可表示为:
(2)

(3)
1.2 混凝土开裂后扭转刚度
在混凝土开裂后,混凝土板的扭矩主要由受拉钢筋网架和受压混凝土压杆来承担,HSU[9]利用Rausch提出的空间桁架模拟法计算得到了钢筋混凝土薄壁结构扭转开裂后的剪切模量Gcr,本文将其扩展到计算波形钢腹板混凝土组合箱梁混凝土顶底板的剪切模量,如式(4)所示:
(4)
式中:nEs=Es/Ec为钢筋与混凝土的弹性模量比值;Gcr为钢筋混凝土板开裂后的剪切模量;ρl为纵向钢筋相对于混凝土板的配筋率,ρl=Al/(2yth);ρt为横向钢筋相对于混凝土板的配筋率,ρt=At/(ths);其中,Al、At分别为剪力流所包围的全部纵向钢筋截面面积和横向钢筋的截面面积;s为横向钢筋的间距。
则混凝土开裂后波形钢腹板混凝土组合箱梁的扭转刚度KI可表示为:
(5)
假设波形钢腹板采用理想弹塑性材料,当波形钢腹板屈服后,波形钢腹板的扭转刚度将变为零。此时钢筋混凝土顶底板的扭转刚度为:
(6)
1.3 波形钢腹板组合箱梁开裂扭矩
沈孔健[8]等通过考虑波形钢腹板组合箱梁普通钢筋和预应力钢筋的影响,提出如下开裂扭矩修正公式:
(7)
式中: 配筋率ρ为ρl与ρt的总和;σ为预应力钢筋在混凝土顶底板上产生的初始压应力;f′c为混凝土圆柱体抗压强度。
波形钢腹板组合箱梁开裂扭率为:
θcr=Tcr/K0
(8)
1.4 波形钢腹板组合箱梁屈服扭矩
波形钢腹板混凝土组合箱梁的屈服扭矩Ty为波形钢腹板屈服时所对应的扭矩,根据薄壁结构扭转理论[10]:
Ty=2A0fτftd+2A0wτytw
(9)
式中:A0f、A0w分别为混凝土顶底板和波形钢腹板剪力流所围成的面积;τf为混凝土顶底板的剪应力,τy为波形钢腹板的剪切屈服应力;td为混凝土顶底板剪力流有效厚度。此时,波形钢腹板的剪应变γw为:
γw=τy/Ge
(10)

γf=γw
(11)
即可求得此时顶底板混凝土的剪应力:
τf=Gcrγf
(12)
因此,将式(10)~式(12)代入式(9)可得:
(13)
1.5 波形钢腹板组合箱梁极限扭矩
根据美国规范ACI 318-14[11]混凝土薄壁结构极限扭矩计算方法,并考虑波形钢腹板的贡献,可得波形钢腹板组合箱梁极限扭矩:
(14)
式中:fty为横向钢筋抗拉强度;对于钢筋混凝土构件α=45°,预应力混凝土构件α=37.5°。同时,纵筋应满足:
(15)
式中:fly为纵向钢筋抗拉强度,由式(15)可得:
(16)
1.6 算例
选取以往波形钢腹板组合箱梁典型试验梁为研究对象,验证本文提出的简化计算方法的准确性。丁勇[12]和MO[1]等对单箱单室波形钢腹板PC组合箱梁开展了纯扭转试验,KO[3]等对单箱单室波形钢腹板混凝土组合箱梁开展了纯扭转试验,沈孔健[13]等对单箱双室波形钢腹板混凝土组合箱梁开展了纯扭转试验。需要说明的是,由既有研究结果[14]表明,单箱双室波形钢腹板组合箱梁的抗扭承载力与同尺寸单箱单室波形钢腹板组合箱梁相近。本文采用新提出的简化计算方法计算以上试验梁的扭矩扭率曲线,并与试验值进行对比,如图3所示。由计算结果可知,本文计算得到的扭矩扭率曲线与试验结果较为吻合,说明本文的计算方法具有较好的准确性。

图3 波形钢腹板组合箱梁扭矩扭率计算值与试验值对比
2 波形钢腹板抗屈曲验算
波形钢腹板局部和整体屈曲临界剪应力验算应按规范[15]要求进行验算,限于篇幅,此处不再赘述。
(17)
式中: 波形钢腹板局部屈曲系数ξ=4+5.34(hw/aw)2,ν为波形钢腹板的泊松比;hw为波形钢腹板的高度。
(18)

局部或整体剪切屈曲参数λs,l(g)可按下式计算:
(19)
式中:fv为钢板的抗剪强度设计值。
为使波形钢腹板组合箱梁设计经济合理,充分发挥波形钢板的抗屈曲能力,在波形钢腹板的设计中应控制剪切屈曲参数λs,l(g)≤ 0.6,使波形钢腹板的剪应力高于剪切屈服应力时,波形钢腹板才发生局部屈曲或整体屈曲。
3 抗剪连接件设计
a. 当发生栓钉剪断破坏时:
(20)
式中:Astd为栓钉截面面积;fstd为栓钉抗拉强度设计值,当栓钉材料性能等级为 4.6级时,取fstd=400 MPa;fcu为混凝土的立方体抗压强度设计值。
b.当发生混凝土压碎破坏时:
(21)
式中:fcd为混凝土的轴心抗压强度设计值;η为群钉效应折减系数。当6 组合箱梁截面剪力流q可取外加扭矩设计值Td所产生的截面剪力流qa和钢腹板所能承受剪力流qw的较小值: qa=Td/(2A0f+2A0w),qw=fvtw (22) 则栓钉的间距s为: (23) 其他类型的抗剪连接件尺寸参数和间距的设计可按规范[15]要求进行设计验算,在此不作赘述。 波形钢腹板组合箱梁抗扭设计可按图4所示设计流程进行设计,具体过程如下所述。 图4 抗扭设计流程Figure 4 Torsional design process 根据外加扭矩设计值Td,首先选取截面尺寸、混凝土强度等级、钢腹板强度等级、钢筋强度等级等。 a. 确定波形钢腹板厚度。将波形钢腹板组合箱梁截面等效为钢板,可初步估算波形钢腹板的厚度。 (24) 式中:A0为截面薄壁中心线围成的面积。 b.确定波形钢腹板承担的扭矩。由于在极限状态下,混凝土顶底板混凝土承担的扭矩较小,可忽略。因此,波形钢腹板承担的扭矩计算如下。 Tw=2A0wtwτy (25) c.确定箍筋承担的扭矩。 Ts=Td-Tw (26) d.确定箍筋的配置。 (27) 验算ρt=At/(ths)≥0.28fct/fty,其中,fct为混凝土抗拉强度。若不满足,取At/(bs)=0.28fct/fty。 e.确定纵筋配置。 (28) 验算ρl=Al/(pfth)≥0.85fct/fly。若不满足,取Al/(pfth)=0.85ft/fly。 f.根据确定的箍筋量和纵筋量,计算极限扭矩Tu,验证是否满足设计要求,否则重复以上步骤,直至满足要求为止。 g.验算波形钢腹板局部和整体屈曲应力是否满足要求,不满足则重复以上步骤,直至满足要求为止。 h.根据第3节内容进行抗剪连接件设计,确定连接件的几何参数和间距。 假定某波形钢腹板组合箱梁扭矩设计值为Td=20000kN·m,其截面尺寸如图5所示。波形钢腹板采用1200型,材料强度为Q345D,混凝土强度为C50,钢筋强度等级为HRB400。据此,对该箱梁进行配筋设计。 (a)箱梁横断面(单位: cm) (b)波形钢腹板(单位:mm) 经计算,x1=4100mm,y1=1535mm,th=265mm(顶底板平均厚度),pf=4100mm,A0=6293500mm2。 a.确定波形钢腹板厚度。 b.确定波形钢腹板承担的扭矩。 Tw=2A0wtwτy=4100×1535×12×180×10-6=13593.96 kN·m。 c.确定箍筋承担的扭矩。 Ts=Td-Tw=6406.04 kN·m。 d.确定箍筋的配置。 3.77 mm。 e.确定纵筋配置。 f.根据确定的箍筋量和纵筋量,计算极限扭矩。 g.经验算,局部剪切屈曲参数λs,l=0.36<0.6,整体部剪切屈曲参数λs,g=0.19<0.6,波形钢腹板局部和整体屈曲应力满足要求。 h.根据第3节内容进行抗剪连接件设计,可采用抗拉强度为400MPa,直径为25mm的双排4.6级栓钉。经计算,单个栓钉承载力为265.38kN,截面剪力流为1.59kN/mm,纵向间距可取为334mm,栓钉间距与直径比为13.4>13,无需考虑群钉折减系数。 采用SHEN[6]等提出的波形钢腹板组合箱梁软化薄膜模型SMMT对本文设计梁的承载能力进行验算,如图6所示。同时,采用本文提出简化计算方法,得到了扭矩扭率三段3式简化直线。由图6可知,本文计算方法得到的扭转全过程计算值与SMMT模型计算得到的结果较为一致。但SMMT模型得到的设计梁极限扭矩不低于22095.3kN·m,比本文极限扭矩计算值稍大,主要原因是本计算方法忽略了混凝土对于抗扭承载力的贡献。同时也表明本文计算方法稍保守,采用此方法进行设计是安全可靠的。 图6 实尺寸波形钢腹板组合箱梁扭矩扭率SMMT计算值与简化计算值对比Figure 6 Comparison of calculated values by SMMT and simplified calculated values of torque and twist in the full-size composite box girder with corrugated steel webs 本文针对波形钢腹板组合箱梁扭转受力全过程的简化计算和设计方法进行研究,给出了结构扭转受力全过程的扭转刚度、开裂扭矩、屈服扭矩以及极限扭矩计算方法,并应用既有试验梁试验结果验证了文中所给简化计算方法的准确性;在此基础上,提出了波形钢腹板组合箱梁抗扭简要设计方法,对比验证结果表明,采用方法进行设计是安全的,可用于波形钢腹板组合箱梁波形钢腹板和配筋设计。需要注意的是,本文仅对波形钢腹板组合箱梁抗扭性能进行设计,最终的结构设计应结合抗弯、抗剪性能进行综合考虑,确定波形钢腹板及钢筋最终布置方案。
4 设计流程

5 设计案例
5.1 波形钢腹板组合箱梁抗扭配筋设计
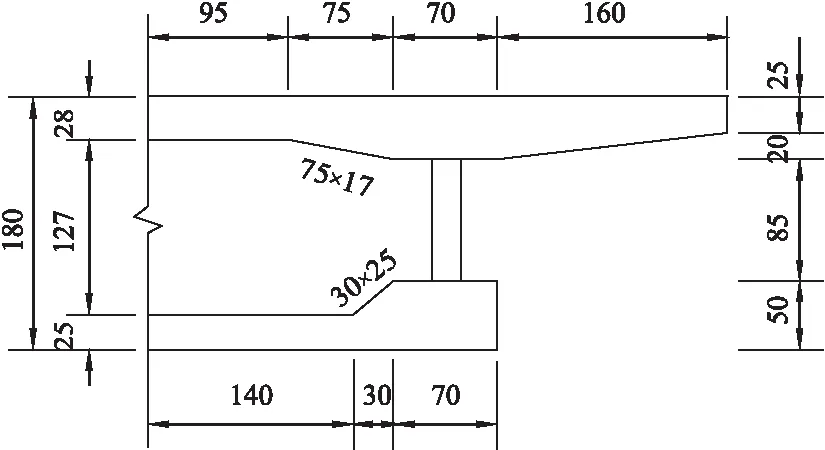
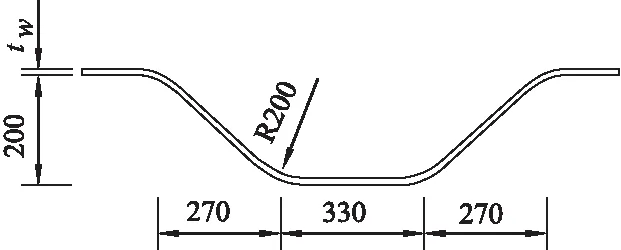

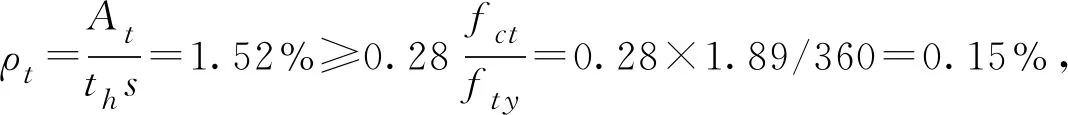


5.2 实尺寸波形钢腹板组合箱梁抗扭承载力验算

6 结论
