基于最小二乘参数辨识的电缆早期电弧故障测距

2021-01-25张璇周正雄朱鹏

湖南电力 2020年6期

张璇，周正雄，朱鹏

(1. 国网湖南省电力有限公司张家界供电分公司，湖南张家界427000；2. 长沙理工大学电气与信息工程学院，湖南长沙410114)

0 引言

地下电缆因为其短距离传输的经济性[1]和恶劣环境下的输电可靠性在城市电网中得到了广泛应用[2-4]。但是在长期运行后, 电缆主体和附件的绝缘电阻会逐渐缓慢降低[5-6], 绝缘的逐步恶化导致电缆从 “安全” 运行状态进入到 “带病” 运行状态[7]。在此期间电缆接头及其附件容易发生局部放电现象, 频繁的局部放电后期逐渐演变成为间歇性的电弧接地故障。从故障波形上看, 此类故障往往发生在电压峰值处, 持续四分之一周期至四个周期内不等。它可能在一段时间内多次发生, 也可能很长一段时间不发生, 直至绝缘击穿, 形成永久性故障[8]。

目前对于这种介于绝缘劣化和永久性击穿之间的间歇性电弧故障研究较少, 国内外提出的测距方法按照理论基础可分为两大类: 阻抗法[10-12]和行波法[9]。文献 [12] 利用故障过渡电阻为纯电阻性质, 以故障电压、电流及线路分布参数模型计算沿线各点的电压与电流实现故障点定位, 但忽略了感抗。文献 [13] 考虑了电缆金属护层结构建立双层阻抗电缆电路模型, 以参数辨识迭代法实现故障点测距, 但增加了模型复杂度, 未充分考虑线路耦合。文献 [14] 针对架空线、电缆多段混合线路, 提出一种利用分段补偿原理的改进双端行波测距新方法。文献 [15] 将零序电压、电流暂态分量的衰减时间常数和频率结合拉氏变换和双曲函数线路模型, 提出一种基于特征根的电缆单端测距方法, 但该算法收敛性差, 测距精度易受外界影响。

针对上述测距方案的不足, 本文通过电缆不同早期故障形式下的状态网络, 结合故障数据采样值, 建立了零模等效电路时域测距方程。对微分方程中的高阶求导问题, 采用正弦逼近拟合零模信号, 从而克服差分近似代替造成的误差大的缺陷。将过渡电阻、故障距离作为模型的未知参数, 代入到测距方程中进行最小二乘参数辨识, 选取合适的数据窗口计算过渡电阻。通过不断移动数据窗口,得到过渡电阻的暂态估计值, 从而解得电缆早期故障距离。

1 电缆早期电弧故障特性

1.1 单芯交联聚乙烯电缆结构

XLPE (交联聚乙烯) 交流电缆主要有两种结构, 即应用于35 kV 及以上电压等级的单芯电缆和35 kV 以下电压等级的三芯电缆。本文中选用的电缆模型如图1、图2 所示, 其中图1 为单芯XLPE高压电缆实物图, 图2 为单芯XLPE 高压电缆剖面示意图。

图1 单芯XLPE 交流电缆实物图

图2 单芯XLPE 交流电缆剖面示意图

单芯XLPE 交流电缆由线芯、内屏蔽层、绝缘层、外屏蔽层、金属护层和外护套组成[16], 其主要结构参数见表1。

表1 电缆主要结构参数

1.2 电缆早期故障等效电路

电缆运行期间, 电缆护层某处绝缘缺陷点会发生频繁的局部放电, 加快了绝缘老化。当缺陷点处含有水汽或者其他介质时, 会与地面产生高压电弧现象并且散发的能量瞬间蒸发水汽使得电弧消失。当发生早期故障时, 电缆故障段的等效电路如图3所示。

图3 电缆单相早期故障等效电路

分析知A 相输入电压为:

式中,Ua为输入端 A 相电压；iaa、ibb和icc分别为各相电流；Ra和La分别为A 相单位长度电阻与电感；Lab和Lac分别为A 相与其他相之间单位互感；Rf和if分别为早期故障电阻和故障电流, 其中Rf近似于时变电弧电阻与固定电阻的叠加；x为故障点距离。

式中,Cag、Cbg和Ccg为单位长度对地电容；Cab、Cac和Cbc为单位长度相间电容。

故障电流if等于剩余电流:

1.3 电缆早期故障电弧模型

本文采用动态Cassie-Mayr 组合电弧模型模拟时变电弧电阻, 此模块在PSCAD 上仿真的电弧电压和电弧电阻结果如图4 所示。可以看出电弧电阻在电流零休期间较大, 燃弧期间阻值近似为零, 能够满足时变特性。

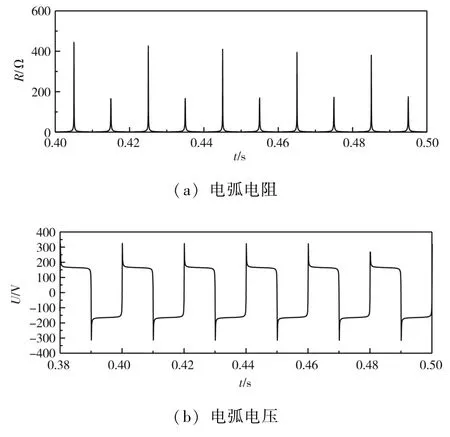
图4 Cassie-Mayr 电弧模型特性

电缆早期故障根据暂态持续时长分为半周波和多周波早期故障, PSCAD 中电缆早期故障仿真结果如图5 所示。可以看出在相同的条件下电缆半周波早期故障一般持续1/2 个周期, 而电缆多周波早期故障可持续1～3 个周期。

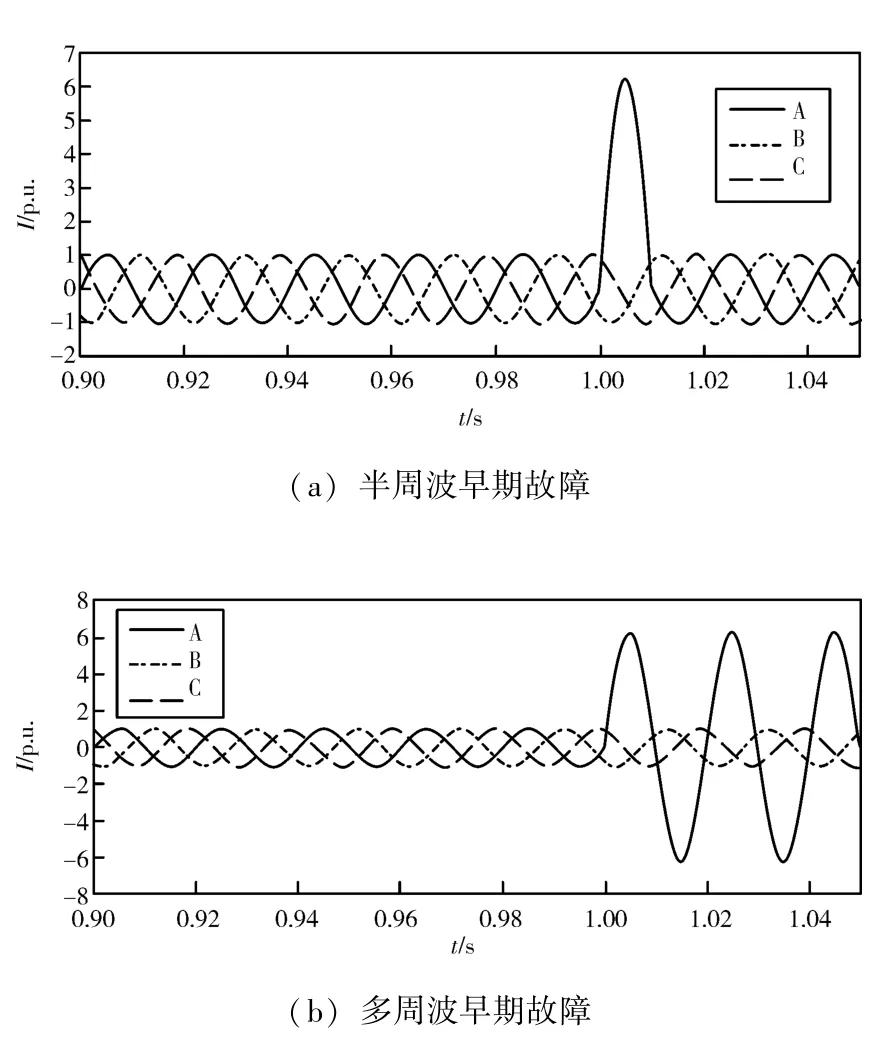
图5 电缆半周波和多周波故障仿真结果

2 测距原理

2.1 故障状态零模等效电路

故障A 相电压的时域微分方程为:

式中,r1、l1分别为线路单位长度一模电阻、一模电感,Rf为故障点至大地的过渡电阻。上式对流过线路电阻和电感的电流乘以零序补偿系数后, 得故障电压和故障电流:

式中,KR、KL分别为电阻及电感分量的零序补偿系数,im0为零模电流, 计算式见式 (6):

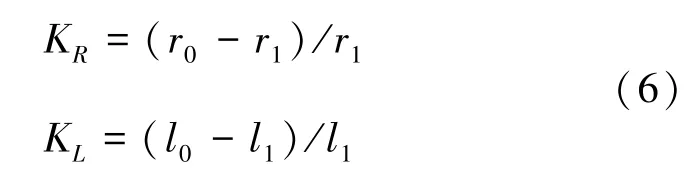
式中,r0、l0分别为线路单位长度零模电阻和零模电感。配电网故障状态下的零模等效电路如图6所示。

图6 配电网故障零模等效电路

由故障点两端的零模电压相等可得到故障距离的微分方程为:

对上式求导得:

其中, 由相模变换可得故障点零模电流为:

可得测距方程矩阵:

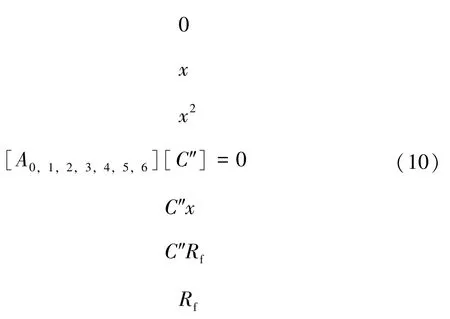
其中, [A0,1,2,3,4,5,6] 为系数矩阵, 可由监测的电缆暂态三相电压、电流求得。

2.2 正弦逼近法计算高阶导

对于系数矩阵中的零模电压、零模电流的高阶求导, 为了减少差分等效带来的误差, 选择利用正弦函数逼近拟合原零模采样波形得到拟合的多项正弦函数表达式, 再求导得到精确的二阶导、三阶导系数。

以m 端的零模电流信号为例, 根据级数原理,零模电流信号的函数表达式可以用不同幅值和不同相位的各次正弦波叠加表示:

式中,an为幅值,ωn为角速度,φn为初相位。

通过不断的修正每项正弦函数的幅值与相位,使拟合函数f(t) 与实际值误差最小。

最后, 通过f(t) 的表达式计算从而得到系数矩阵[]。

2.3 芯―护层故障 (c-s)

当电缆导芯与金属护层之间的绝缘因老化而破坏时, 两者之间的过渡电阻会增加一个金属护层的过渡电阻分量, 此时早期故障零模等效电路如图7 所示。

图7 c-s 早期故障零模等效电路

式中,rs为电缆金属护层单位长度电阻值。

此时电缆早期故障测距方程式 (10) 变为:

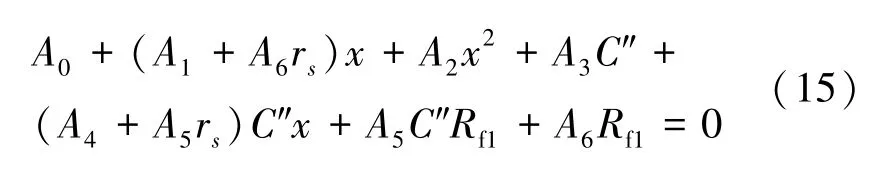
2.4 芯—护层接地故障 (c-s-g)

当电缆在芯—护层故障的基础上, 发生局部外护套破损时, 电缆的铠装层直接接地或间接接地(经小阻抗) 时的早期故障零模等效电路如图8所示。

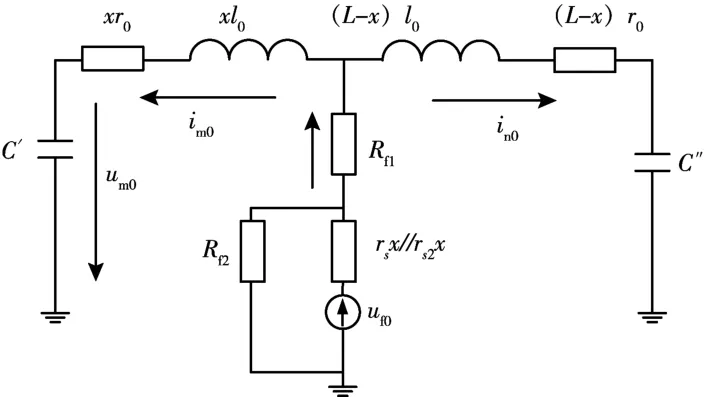
图8 c-s-g 早期故障零模等效电路

此时的过渡等效电阻为:

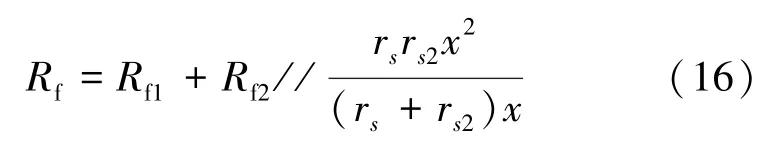
式中,rs2为外铠装层单位长度电阻。

此时电缆早期故障测距方程式 (10) 变为:

3 测距流程

正常运行状态下, 电缆缆芯与铜屏蔽层之间的主绝缘和钢带铠装层与大地之间的外护套绝缘状态良好, 理论上故障电阻Rf1和Rf2为无穷大。当电缆发生芯―护层故障后, 电缆主绝缘被破坏,Rf1降为某一定值,Rf2/Rf1比值较大。当电缆发生芯―护层接地故障后, 电缆两处绝缘均被破坏,Rf1和Rf2同时降低, 且两者均与电弧长度有关, 因此Rf2/Rf1比值较小。可利用这一特征区分电缆早期 (cs) 自恢复故障与 (c-s-g) 自恢复故障。

对于公式 (15) 和公式 (17), 系数矩阵[A0,A1,A2,A3,A4,A5,A6] 由式 (11) 求得,其中高阶导部分用正弦逼近法消除差分误差。当线路两端的监测装置或者其他录波装置发现监测波形中出现电压峰值下降, 并持续时间在四分之一周波到两个周波左右, 期间电压接近恒定值等特征时,即可启动自恢复故障检测流程, 整体步骤如下:

步骤一: 选取合适的数据窗口, 记录故障后的母线电压、线路电流, 即uma(k)、umb(k)、umc(k)、ima(k)、imb(k)、imc(k) , 利用相模变换得到零模电压、零模电流计算值序列um0(k)、im0(k)。

步骤二: 设置初始值, 包括故障距离初始值、过渡电阻初始值和对地电容初始值等。

步骤三: 将初始值代入到芯―护层故障测距方程式 (15) 进行最小二乘参数辨识, 得到故障电阻Rf1和Rf2, 根据两者比值Rf2/Rf1辨别早期自恢复故障类型。

步骤四: 再将步骤二中初始值代入到已识别出的故障类型相对应的故障测距方程中, 进行最小二乘参数识别, 求解方程组未知常数之一的过渡电阻。

步骤五: 不断地移动数据窗口, 重复步骤四,计算线路过渡电阻。如果随着数据窗口的移动所得到的过渡电阻估计值稳定在一个数值范围, 给出此时对应的故障距离估计值。基于最小二乘参数辨识的电缆早期电弧故障测距整体流程如图9 所示。

图9 测距流程图

4 仿真验证

在PSCAD/EMTDC 中建立10 kV 系统三相单芯电缆供电模型, 模型参考文献 [7]。其中电缆主要结构参数见表1, 电缆长度L设为10 km, 设定距离首端6 km 处发生半周波自恢复故障 (c-sg)。以10 kHz 的采样频率监测三相电压、三相电流值, 并以10 个采样点为一个数据窗, 通过测距方程得到的过渡电阻辨识参数和故障距离估计曲线如图10 所示。

图10 半周波故障的参数估计曲线

在不断地移动数据窗口过程中, 故障状态时的过渡电阻慢慢趋于一个恒定值, 并在小范围内波动。将过渡电阻代入测距方程求解出故障距离, 其距离估计曲线如图10 所示。在约20 个采样点处估计距离达到6.2 km, 而后在±0.3 km 内波动, 过渡电阻在12.2 ～13.1 Ω 波动。定义故障距离估计值与真实值的相对误差来评价算法的准确性:

改变采样频率, 减少一个数据窗口的采样点数量, 分别取每个数据窗口采集 5、10、15、20 个数据点, 算法的相对误差曲线如图11 所示。

图11 不同采样点的相对误差曲线

图11 可以看出, 一个数据窗口内的采样数量N越高, 算法的精确性与稳定性越好。在N＝10 时可以将相对误差控制在±5%内, 在N＝20 时可以将相对误差控制在±3%, 同时考虑到算法收敛时长应尽量较短, 在后续仿真实验中可取N值为15。在其他条件不变的情况下, 设置不同的故障距离,观察芯―护层接地故障下的电缆半周波、多周波早期故障下的故障点距离估计结果和相对误差, 统计见表2。

表2 芯―护层接地故障测距结果

改变电缆早期故障形式, 当电缆发生导芯―护层自恢复短路故障时, 在导芯和护层之间会产生电弧电压, 线路参数和采样频率保持不变, 故障距离估计平均相对误差由平稳数据窗下的估计值计算得到, 其结果见表3。

表3 芯―护层故障测距结果

从表2 和表3 可以看出, 无论是芯―护层接地故障还是芯―护层故障, 在其他条件不变时, 多周波早期故障因为暂态信号波形相较于半周波早期故障持续时间更长、更稳定, 易于监测设备提取信号至测距算法计算故障距离, 故多周波故障下的测距结果更好。随着故障距离地不断增加, 沿线传播的暂态信号衰减严重, 此时两种早期故障的识别率均会有不同程度的降低。