基于共线方程原理的全站仪对中误差改正研究

陈正港 胡 川 舒 敏 何永红

（湖南科技学院 土木与环境工程学院，湖南 永州 425199）

21 世纪以来，随着微型计算机的发展和嵌入式开发的不断发展，各类新型测绘仪器层出不穷，例如GPS、测量机器人、电子水准仪、全站仪等。并且一些电子仪器还在不断地优化升级，其中全站仪就是最为典型的代表。全站仪是一种集测角、测距为一体，且能进行数据计算和临时储存的高科技测量仪器。

21 世纪80 年代以来，一些复杂的多功能软件不断地被加载到全站仪的微型计算机内，偏心测量、对边测量等应用测量得到满足，不仅测量精度得到提高，并能与外接设备进行数据双向通讯。全站仪误差检定的结果可以内置于全站仪的微处理器内，测量的结果经过检定修改后显示到显示屏上。使用其获取的测量数据精确可靠，操作简单，可有效地减少人力资源，此外还能尽量减少测量数据的人为误差。本科生在学校学习全站仪时，所有的操作流程都比较简单，但对中这一步骤比较繁琐复杂，一般需要2∼3 次重复对中，才能达到对中的要求。如果未达到对中的要求就进行测量，则采集的数据的精准度是无法保证的。另外，因测量时间或其他原因导致达不到对中要求也容易被忽略。

近年来，随着数字摄影测量的高速发展，其研究成果也颇为丰硕，我们可以借鉴一些相关成果用于解决以上问题。杨国东等[1]分析了倾斜摄影测量技术的发展概况、基本原理及外业数据获取，探讨了影像数据的匹配、正射影像纠正以及平差等处理的关键问题并进行总结。徐永等[2]总结了国内外与摄影测量系统校准技术相关的研究与应用，并在此基础上研究摄影测量系统的校准技术和方法，研制专用的标准器和校准装置，拟制定一套完整的工业摄影测量系统校准规范。张大春[3]研究了多基线近景摄影测量系统，从摄影、相机检校、布点方案、数据处理到立体测图全过程的关键技术。

本文结合摄影测量原理和坐标正反算原理，开发一套数据处理程序，基于全站仪在第一次对中整平后，激光斑点在测钉之上，根据一系列测量参数，在电子计算机上自动对采集数据进行批量处理，由此进行补偿改正，使数据值精准可靠。

1 设计构思

首先在站点上对全站仪进行对中整平，使对中激光斑点在测钉上（激光斑点和测钉中心之间的高差很小，可假定两点在同一个水平面上），在进行数据采集之前，在全站仪的一侧安转一个航空摄影机（见图 1），且带有光学框标，内方位元素已知为（ x0,0y, f ），像空间坐标系与像空间辅助坐标系重合，且像空间辅助坐标系的Z 轴（图2 中的w）垂直于地面，如图2 所示，测量4 组激光斑点到后视定向点的距离，并取平均值L1并记录，用钢卷尺测量测钉中心到航空摄影机摄影中心的实际距离 4次，取平均值为Z1，测量航空摄影机摄影中心到全站仪中心的实际距离4 次（航空摄影机摄影中心和全站仪中心的连线垂直于全站仪中心的重力方向），取平均值为Z2，运用勾股定理推出全站仪中心到激光斑点的实际距离Zs，再将航空摄影机所拍摄的影像导入到电子计算机中，量测影像上激光斑点到测钉中心之间的距离，运用摄影测量中三点（物点、像点、摄影中心）共线及三角形相似原理，可计算出激光斑点到测钉中心之间的实际距离L2。利用已知的站点中心和后视定向点坐标算出两点之间的实际距离 L3，从而对 L1，L2，L3之间的数值大小进行判断，构建出相应的对中误差模型，最后运用坐标正反算计算得出改正值Δ x1，Δ y1。将所采集的数据加上改正值，即可得出更精确的地面点三维坐标。基于此，利用VB 语言实现该方案的软件部分，输入摄影测量参数值及全站仪测量数据，即可自动对测量数据进行改正补偿，提高全站仪测量精度。

图1 全站仪安装航空摄影机图

2 设计原理

本文主要是将摄影测量原理和坐标正反算原理进行有效结合。以下是这两个理论的相关知识以及全站仪坐标定向的原理。

2.1 全站仪坐标定向的原理

全站仪中的后视定向功能，是依据已知的设站点与后视点坐标，全站仪内部的程序计算出两点所在直线的坐标方位角；“坐标方位角”是以某点的坐标北方向开始，顺时针方向旋转到目标直线的水平夹角；以坐标北方向为坐标系的X 轴，且以与X轴正交的为Y 轴，则相当于为仪器设定好了一个平面直角坐标系。

2.2 摄影测量共线方程原理

如图2 所示，令坐标系O-XYZ，S-uvw 分别为地面摄影测量坐标系、像空间辅助坐标系，且两种不同坐标系的各个坐标轴对应平行。交于S＇，与地面交于O，S 点及A 点在坐标系O-XYZ中的坐标分别为(0，0，Zs)和(X，Y，0)，S＇、像点a 在坐标系 S-uvw 中的坐标分别为（0，0，-f）、（u，v，-f）。由S，a，A 三点共线和相似三角形原理可得

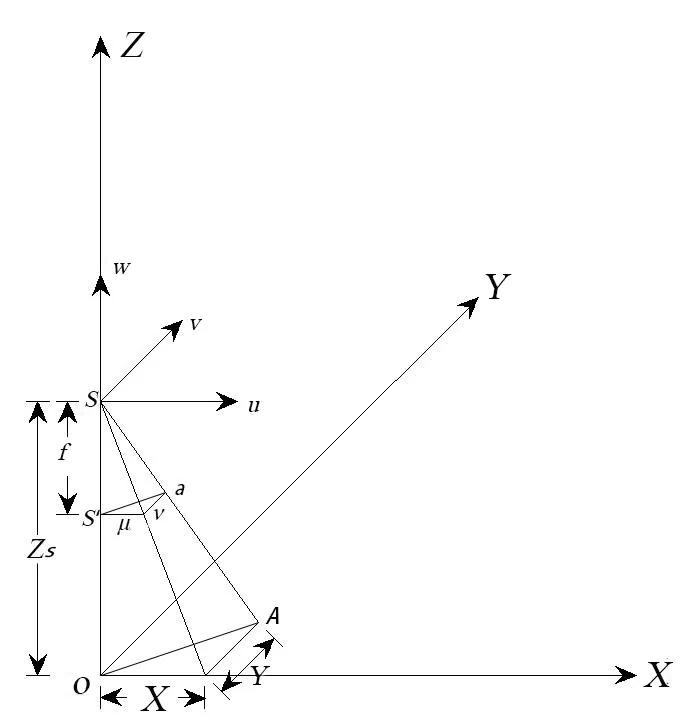
图2 中心投影构像关系示意图

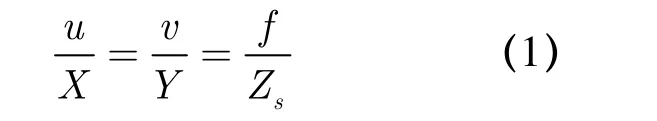
Zs可通过钢卷尺测量得出，f 已知，u、v 可以从影像量测得到，根据这些参数由式(1)可直接计算出X，Y 的值，最后运用勾股定理可计算出O 点到A 点的直线距离SOA。

2.3 坐标正反算原理

坐标方位角的推算，如图3 所示，已知直线AB的坐标方位角和反坐标方位角为分别为αAB和αBA，B 点处的观测角为β，当β 为左角时（见图3），则直线BC 的坐标方位角αBC为[4]

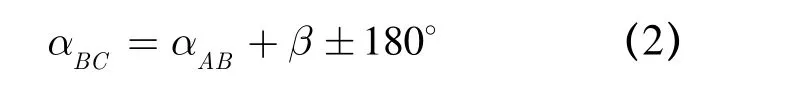
当β 为右角时（见图4），则直线BC 的坐标方位角 αBC为

综上所述，可得出坐标方位角αBC的推算公式为

如果推算出的坐标方位角大于 360°，则应减去360°，如果出现负值，则应加上360°。

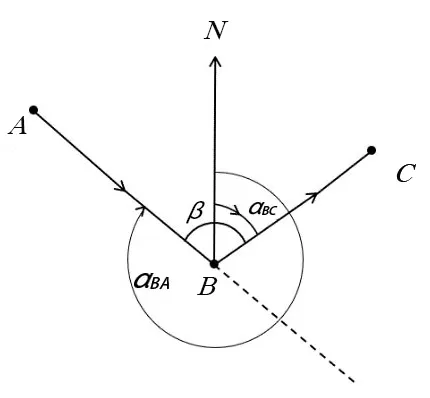
图3 观测角为左角的情况

图4 观测角为右角的情况

2.3.1 坐标正算原理

图5 坐标正反算

如图5 所示，A 为已知点，已知A 点至B 点的水平距离SAB和坐标方位角αAB，求得B 点坐标(XB，YB)称为坐标正算。结合图5 可得

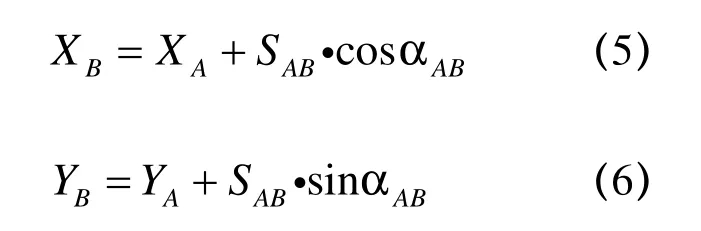
2.3.2 坐标反算原理

如图 5 所示，A，B 两点为已知点，其坐标分别为（XA, YA）和 （XB, YB），则坐标反算是求两点之间的水平距离SAB和坐标方位角αAB。结合图5可得

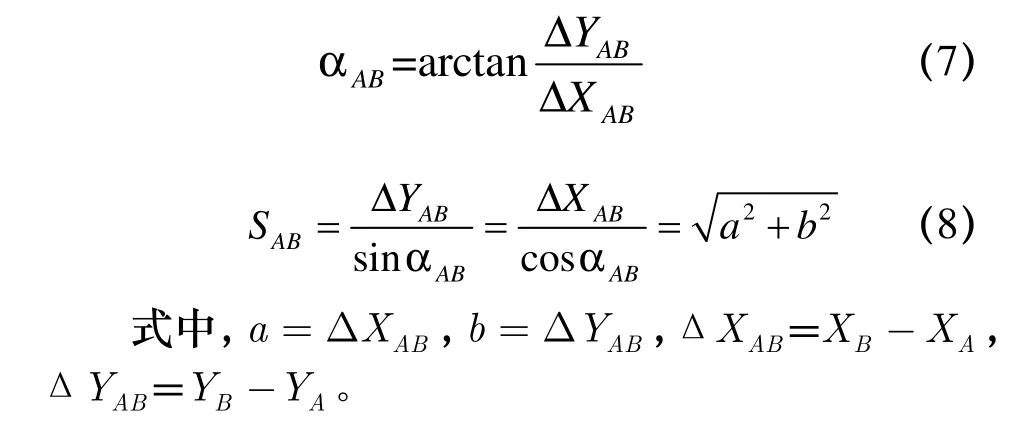
2.3.3 对中误差改正模型

对中误差的类型在实际中分为4 种类型。

在进行后视定向之前，站点A 点和后视定向点B 点的坐标已知，C 点为激光斑点，令L1为B，C之间的距离，L2为A，C 点之间的距离，L3为A，B之间的距离（L1，L2，L3值均已知），运用式（7），可推出A，B 两点的坐标方位角αAB。

类型一：

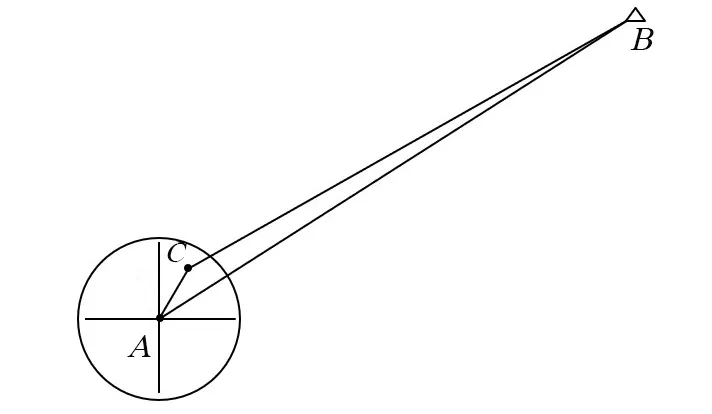
图6 对中改正误差类型一

由图6 所示，根据余弦定理可得

于是，

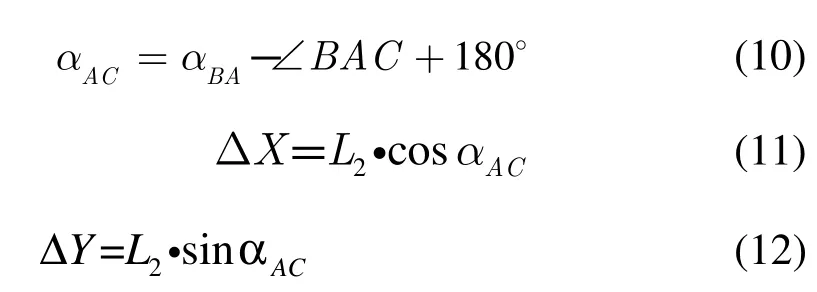
即对中误差的改正值为

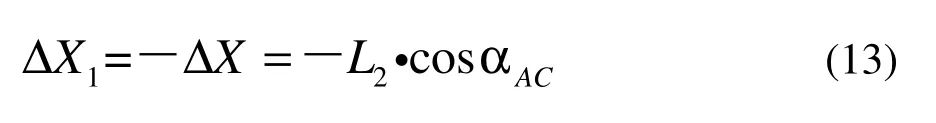
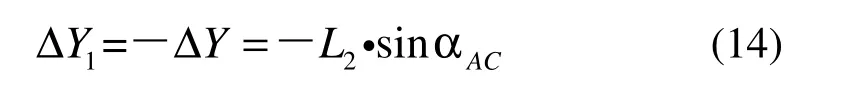
类型二：

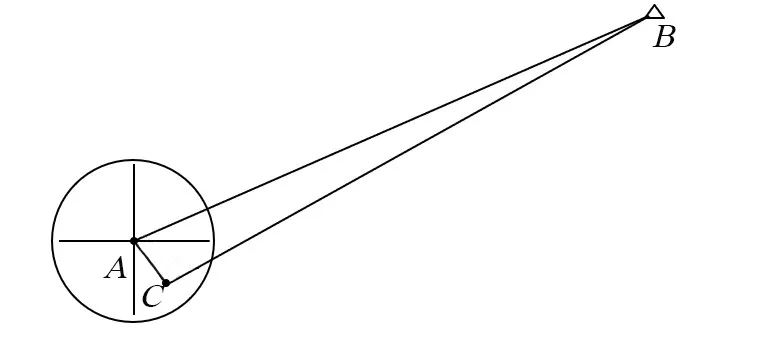
图7 对中改正误差类型二

由图7 所示，由余弦定理可推出

于是，

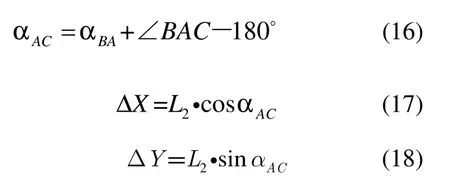
即对中误差的改正值为：

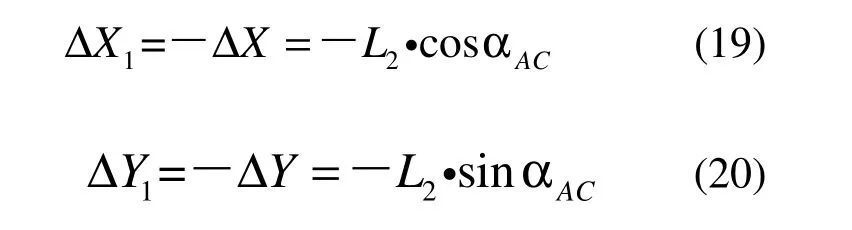
类型三：

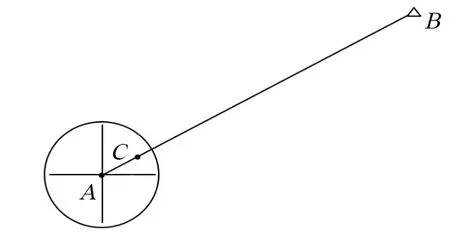
图8 对中改正误差类型三

由图8 所示，可得，

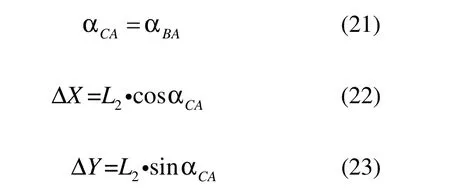
即对中误差的改正值为，

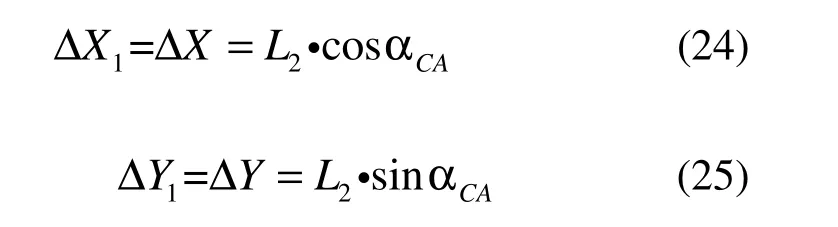
类型四：

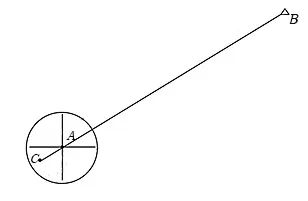
图9 对中改正误差类型四

由图9 所示，可得

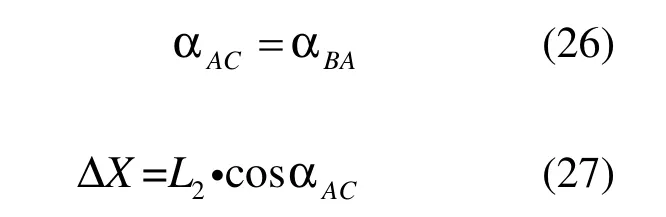
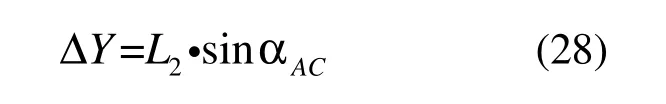
即对中误差的改正值为

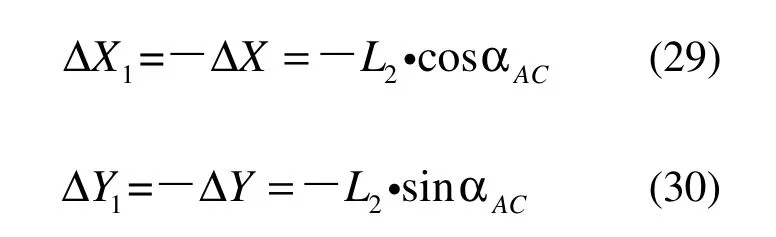
综上所述对中误差的4 种情况以及相对应的改正值，在外业数据采集完成后，批量将每个数据的（X, Y）值都加上相应的（ΔX1, ΔY1），即可求出精准的外业数据值。

3 作业流程

全站仪对中误差改正作业流程图如图10 所示。

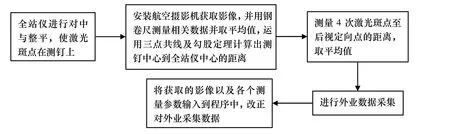
图10 全站仪对中误差改正作业流程图

基于VB 语言实现以上数据处理过程，其数据处理程序界面如图 11 所示，导入航空摄影机拍摄的图片和采集的三维数据文件，输入各测量参数值、测钉中心坐标以及后视定向坐标，单击运行，即可输出对中误差的改正值以及改正后的三维数据文件。

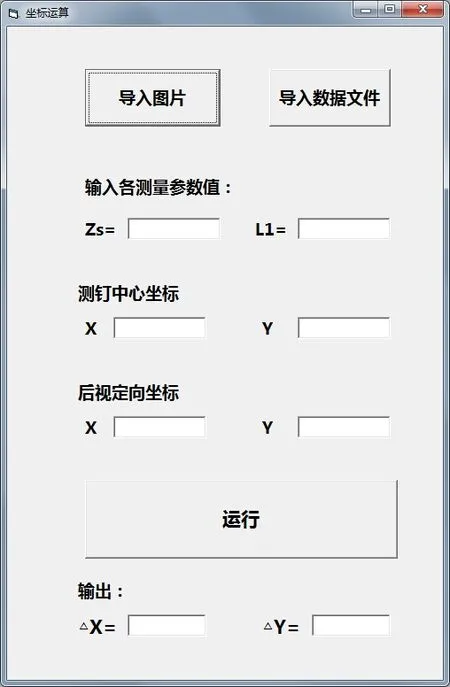
图11 数据处理程序界面

4 结 语

根据上述设计理论，进行误差改正补偿模型的程序编程与测试，测试数据结果显示数据处理程序较为精准，满足测量的精度的要求。但由于天气等原因导致结果存在仪器误差的影响，因此，在使用仪器时，还应注意以下事项：（1）应尽量选择在光线充足的条件下使用航空摄影机，以保证图片的清晰度；（2）测钉的颜色应与激光的颜色不同，以便对激光斑点的识别；（3）激光斑点应处于测钉的钉帽范围之内，以保证高程数据的精准度。