立体交叉隧道地震动力响应分析

石龙飞

(新疆维吾尔自治区交通规划勘察设计研究院，乌鲁木齐 830006)

1 引言

21 世纪是人类利用开发地下空间的世纪，由于城市地面土地有限和交通压力增长， 所以现在要大力发展利用城市地下空间。钱七虎院士也做了关于《城市可持续发展和地下空间开发利用》的报告，强调了对地下空间的开发利用[1-3]，现在很多一线城市都在发展地铁网络，相互穿插情况比较多。人们更加注重地面构筑物的抗震减震，相反忽略了对地下结构的抗震减震的研究[4]。但是日本关东地震、“5·12”汶川特大地震等地震，造成了围岩断层破裂区、 二次衬砌不足或施工质量较差的衬砌段隧道破坏严重，尤其是破坏后地下结构维修难度大，不能及时使生命线在短时间内贯通。 在隧道选线、设计、施工和维修等各个阶段都要考虑抗震设防理念[5]。

2 数值模拟

2.1 地震波的选取

本文地震动力的输入采用的是加速度输入方法，其峰值加速度为0.32 g 的人工合成波， 与地震设防烈度比较为地震基本烈度为Ⅷ度。 加速度反映了地面地震反应的最强烈部分，相同条件下，加速度越高，工程结构物反应越强烈。《城市轨道交通结构抗震设计规范》[6]规定了选择地震波持续时间， 需保证所选择的持续时间应包含峰值加速度， 且持续时间不得少于结构基本周期的5～10倍。 本文的峰值加速度为8.66 s 时的0.32 g，持续时间为0.02 s，整个时程为9.02 s，符合规范要求。加速度时程图，时间历程为0.00～9.02，峰值加速度为0.32 g，见图1。

2.2 动力分析计算模型

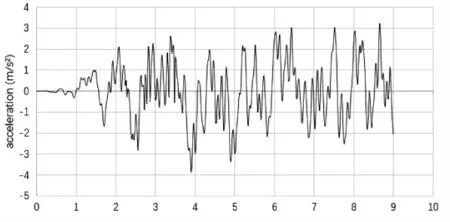
图1 峰值加速度为0.32 g 时程曲线

模型大小为(100×100×100)m 的立方体，用有限域内的土体模型拟在无线域中的受力。 模型底面约束所有自由度，左右两侧及前后两侧施加黏弹性人工边界。土体分成两层上半部分采用Ⅴ级围岩，下半部分采用Ⅳ级围岩，用solid185 单元进行模拟。 衬砌单元用shell63 单元进行模拟。没有考虑初衬，利用加强围岩参数来考虑初衬的支护作用。 采用X 方向激震，对隧道进行动力响应分析。 围岩及支护物理力学参数见表1。

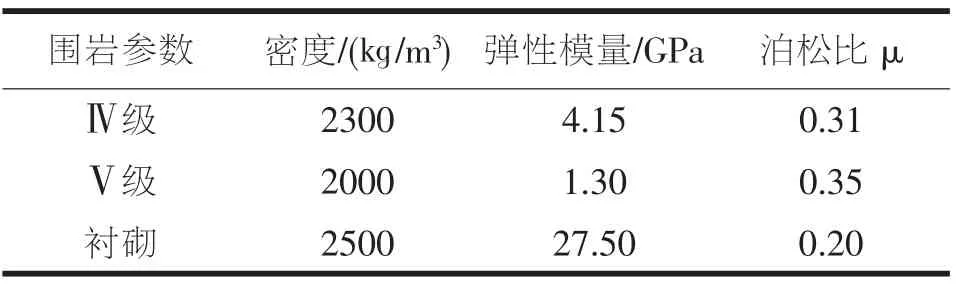
表1 围岩及衬砌物理力学参数

为了确定正交立体交叉隧道不同净距对立体交叉隧道地震反应的影响程度，本例取净距为0.5D、1.0D、1.5D、2.0D(D 为最大洞径)4 种不同工况进行地震作用下正交立体交叉隧道地震动力响应分析。

下面仅列出1.5D 模型如图2。

3 立体正交隧道不同净距X 方向激震计算结果与分析

图2 立体正交隧道1.5D 净距计算模型

本节采用峰值加速度为0.32 g 时程曲线， 从模型底部开始沿X 方向一致激震，进行动力响应分析。 主要分析衬砌关键部位(拱顶、拱底、两侧拱腰及2 条45°线)，主要监测这些位置的X 方向位移、Y 方向的位移、第一主应力、第三主应力。 各监测点如图3 所示。

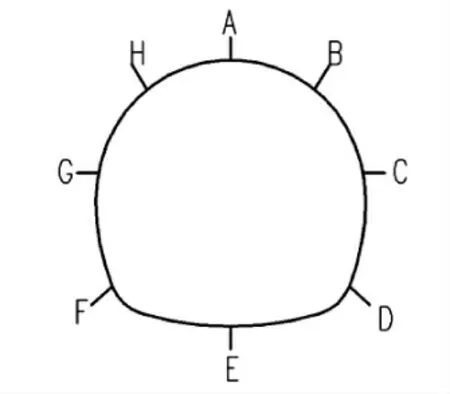
图3 隧道衬砌断面位移、应力监测点位布置图

应力分析： 对于正交立体交叉隧道不同净距(0.5D、1.0D、1.5D、2.0D)下分别取时程中2 s、4 s、6 s、8 s 时刻衬砌不同主应力不同时刻峰值见表2。

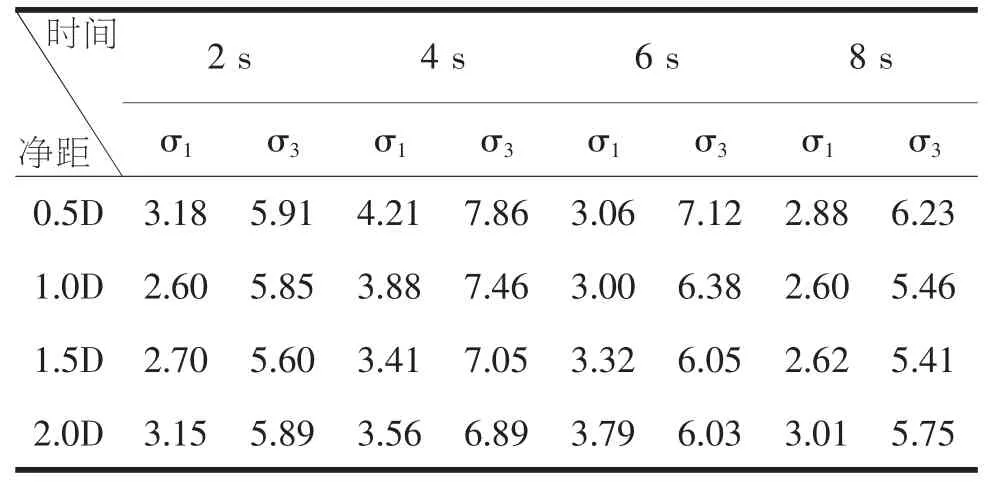
表2 衬砌不同净距主应力峰值(单位：MPa)

由表2 中数据分析可知：在0.5D～1.5D 内，衬砌同一主应力随着净距减小而增大， 最大拉应力递减在4 s 时刻从4.21 MPa 降到3.41 MPa， 减小了19%。 但在1.5D～2.0D 的时刻出现突然陡增的现象， 最大递增出现在6 s，从3.32 MPa 递增到3.79 MPa，增大1.14 倍；这说明立体正交隧道之间的净距并不是越大越好，1.5D 净距是最合理的净距。 如果考虑最合理的净距1.5D 的条件下，在整个时程中最大拉应力为2 s 时刻的3.41 MPa， 已经超过混凝土C30 的抗拉强度设计值1.47 MPa, 说明衬砌将会出现拉裂现象，不能满足设计使用要求，二衬抗拉强度储备不足；最大压应力为7.05 MPa，远小于混凝土的抗压强度15 MPa，衬砌受压不会出现破坏。 隧道衬砌的第一主应力和第三主应力在同一净距下， 不同时刻不是出现单调递增或者单调递减的现象， 这也反应了结构在地震作用下的复杂性，并不具有单一性。

位移分析：位移主要监测上下隧道交叉部位的拱顶、仰拱、拱腰、拱脚、拱肩各点(即点ABCDEFGH)，查看各点X 向和Y 向位移。分析地震对上侧隧道位移影响大还是下侧隧道，以及不同净距对位移的影响。 各点位移见表3。

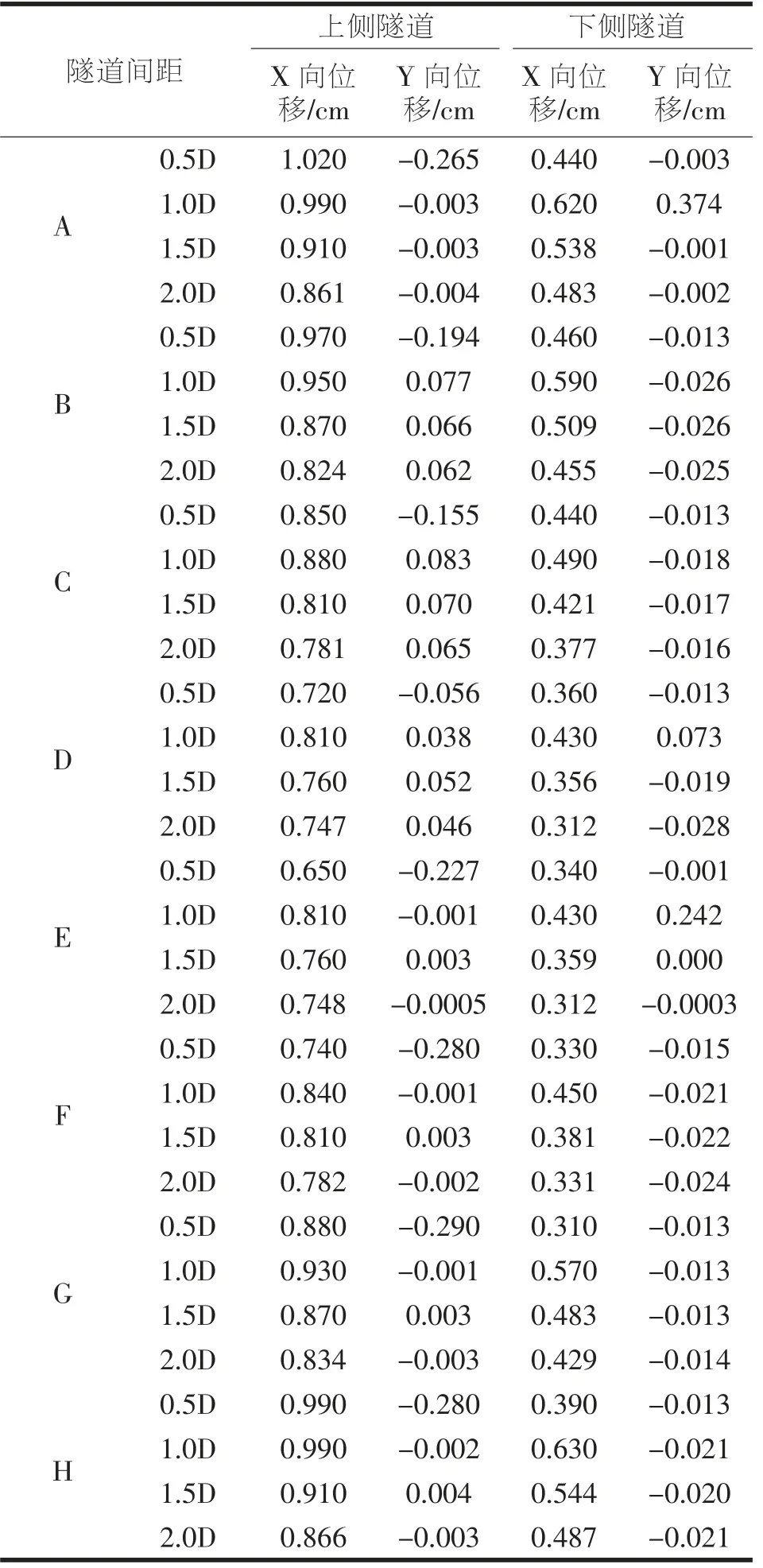
表3 上下隧道交叉部位各监测点位移峰值

由表3 数据分析可知，X 方向地震波作用下，不同间距下，X 方向的位移比Y 方向位移大很多，说明隧道衬砌整体位移与地震波的激震方向关系很大。 即地震波在那个方向激震，哪个方向的位移就最大。对于同一个点的位移，上侧隧道的位移比下侧隧道的大很多，上侧隧道所有监测点中为0.5D 时A 点的位移最大，为1.02 cm，下侧隧道所有监测点中为1.0D 时B 点的位移最大，为0.59 cm。上侧隧道最大位移是下侧隧道最大位移的1.73 倍，这说明正交立体交叉隧道中，上侧隧道比下侧隧道更危险。在各监测点中，位移较大的为A 和H 点，应力集中较大。 上侧隧道X 向峰值位移，随着净距增大而减小，下侧隧道X向峰值位移从1.0D～2.0D 逐渐减小，在1.0D 时达到最大值，从位移角度来看隧道并不是间距越大越好，也不是越小越好， 综合考虑认为1.5D 和2.0D 比较适合正交隧道抵抗位移变形。

净距为0.5D 时衬砌拱顶A 点的X 方向位移和Y 方向位移时程如图4～5 所示(仅列出部分位移图)。

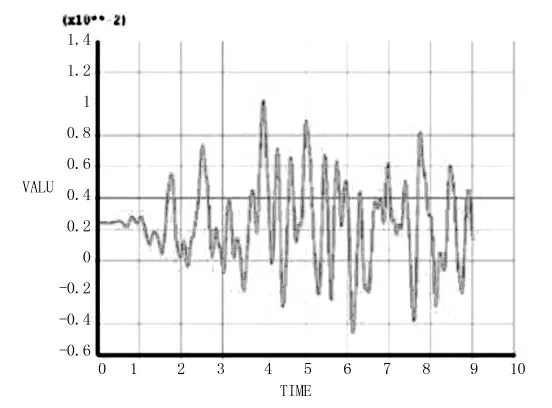
图4 0.5D 净距上侧隧道衬砌A 点向X 位移图

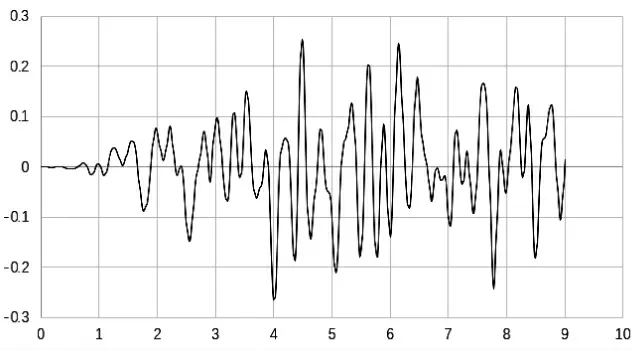
图5 0.5D 净距上侧隧道衬砌A 点向Y 位移图

按弹性力学理论，拱顶是最易产生拉应力的位置，如果拱顶沉降位移过大会产生较大拉应力， 拉应力超过混凝土抗拉强度混凝土可能会产生裂缝， 所以拱顶位移应该重点关注。 从图4～5 知拱顶最大位移产生于净距为0.5D 洞径，位移值为2.6 cm。 在新奥法施工中，拱顶最大位移为2 cm，此时的位移比施工控制值还要大，说明隧道已经存在安全隐患。 上侧隧道振动位移明显大于下侧隧道，说明净距太小对交叉隧道衬砌拱顶位移非常敏感，而且在0.5D～1.0D 洞径发生突变，说明0.5D 洞径是非常危险的。

在立体交叉隧道中通常直观地认为交叉部位应该是最危险的，但是洞口部位也是比较危险的。根据前面分析可以确定上侧隧道更加危险，下面就讨论在X 向激震下0.5D 净距上侧隧道距洞口段0 m、5 m、10 m、20 m、40 m的范围对X 位移进行分析，如表4 所示。

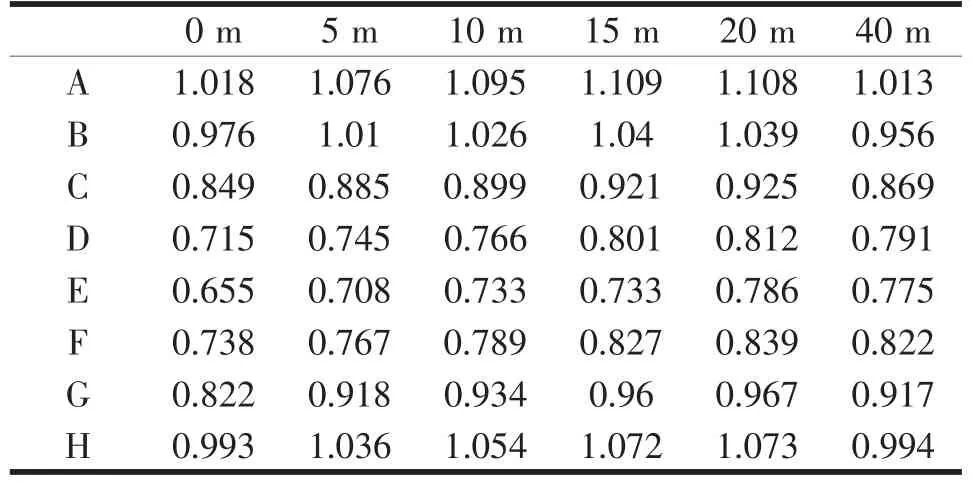
表4 0.5D 净距上侧隧道不同位置位移(单位：cm)

从表4 数据分析可知， 立体交叉隧道上侧隧道各监测点位移距洞口20 m 范围内是随距离的增大而增大，基本上在20 m 位置出现峰值， 从20～40 m 内位移逐渐减小。 可以得出：最大位移值并不发生在交叉部位和洞口，而是发生在距离洞口15～20 m 范围。

4 结论

本文针对城市地铁、轻轨快速发展，相互穿插，相互影响的问题， 着重分析了立体交叉隧道在地震作用下的动力响应分析。从立体正交隧道不同净距，得出了合理的净距。

(1)对立体正交隧道不同净距(0.5D、1.0D、1.5D、2.0D)进行分析，通过应力和位移对比分析，确定了1.5D 净距是最合理的。

(2)0.5D 净距下正交隧道位移最大值发生在距洞口段15～20 m 内，并不发生在洞口和交叉部位。