二阶锥权互补问题的一类含参数效益函数

2021-01-22迟晓妮崔然然杨绮丽

桂林电子科技大学学报 2020年4期

关键词：二阶效益向量

迟晓妮，崔然然，杨绮丽，赵敏

(1.桂林电子科技大学数学与计算科学学院，广西桂林 541004;2.桂林电子科技大学广西密码学与信息安全重点实验室，广西桂林 541004;3.桂林电子科技大学广西自动检测技术与仪器重点实验室，广西桂林 541004)

n维二阶锥Kn定义为

Kn={x=(x1;x2)∈R×Rn-1:x1≥‖x2‖}，

考虑二阶锥权互补问题(WSOCCP)：寻找一向量ζ∈Rn，使得

(1)

其中F(ζ):Rn→Rn为连续可微函数，w∈Kn为给定的权向量。当权向量w为零向量时，式(1)退化为二阶锥互补问题(SOCCP)[1]：

(2)

作为一类重要的锥优化问题，WSOCCP是Rn上的权互补问题(WCP)在二阶锥上的推广，其在经济学、力学、工程设计等方面有着广泛的应用[2]。WCP中非零权向量的存在使得WCP[3-5]的理论和算法比互补问题(CP)复杂得多，因此目前关于WCP的研究并不多见，如Zhang[6]运用光滑牛顿法求解单调线性WCP，Tang[7]给出一种新的光滑算法求解大规模线性WCP。

下降算法是求解CP的有效算法[8-9]，其基本思想是基于效益函数将原问题转化为一个等价的无约束极小化问题[10]，利用下降算法求解此极小化问题，进而得到原问题的解。

鉴于此，提出一类含参数二阶锥权互补函数，构造WSOCCP的效益函数，讨论其光滑性，并基于此效益函数将WSOCCP转化为无约束极小化问题，利用下降算法求解，从而得到原问题的解。

1 预备知识

与二阶锥相伴的欧几里得约当代数有如下性质[11]。

对任意

x=(x1;x2)∈R×Rn-1,y=(y1;y2)∈R×Rn-1，

x和y的约当积定义为

定义箭形矩阵

其中I为适当维数的单位阵，易证

定义1(谱分解) 对任意

x=(x1;x2)∈R×Rn-1，

与二阶锥相伴的谱分解定义为

x=λ1(x)u1(x)+λ2(x)u2(x)，

谱值λ1(x)、λ2(x)和谱向量u1(x)、u2(x)定义为

λi(x)=x1+(-1)i‖x2‖,i=1,2,

其中ω∈Rn-1为满足‖ω‖=1的任意向量。对任意x∈Rn，有

2 一类含参数效益函数

定义函数φτ(x,y):Rn×Rn→Rn为

(x+y)，

(3)

其中：参数τ∈[0,4)；w∈Kn为给定的权向量。定义效益函数ψ(x,y):Rn×Rn→R为

(4)

则式(1)等价于无约束极小化问题：

minf(ζ)=ψ(ζ,F(ζ))。

(5)

引理1令

(h1;h2)∈R×Rn-1，

(6)

h1=‖x‖2+‖y‖2+(τ-2)xTy+(4-τ)w1，

(7)

h2=2x1x2+2y1y2+(τ-2)(x1y2+

y1x2)+(4-τ)w2，

(8)

对任意

x=(x1;x2)，

y=(y1;y2)∈R×Rn-1，

w=(w1;w2)∈Kn，

若h2≠0，则

证明运用Cauchy-Schwartz不等式可得

成立。将

(9)

U=λ1(h)‖h2‖2=(h1-‖h2‖)‖h2‖2=

[‖x‖2+‖y‖2+(τ-2)(x1y1+x2Ty2)+

(4-τ)w1]‖h2‖2-[4x12‖x2‖2+

4y12‖y2‖2+(τ-2)2(x12‖y2‖2+

y12‖x2‖2)+(4-τ)2‖w2‖2+8x1y1x2Ty2+

2(τ-2)2x1y1x2Ty2+4(τ-2)(x12x2Ty2+

x1y1‖x2‖2+x1y1‖y2‖2+y12x2Ty2)+

4(4-τ)(x1x2Tw2+y1y2Tw2)+

2(τ-2)(4-τ)(x1y2Tw2+y1x2Tw2)]‖h2‖，

x1x2Tw2+2(τ-2)(x12x2Ty2+x1y1‖x2‖2+

x1y1‖x2‖2+y12x2Ty2)+(τ-2)×

(4-τ)(y1x2Tw2+x1y2Tw2)+(τ-2)2×

(x1y1x2Ty2+y12‖y2‖2)+2(τ-2)×

(x12x2Ty2+x1y1‖y2‖2)+(τ-2)2×

(x12‖y2‖2+2x1y1x2Ty2+y12‖x2‖2)+

则由w=(w1;w2)∈Kn得，

y1y2Tw2+(τ-2)x1y2Tw2+(τ-2)×

因此，结合Cauchy-Schwartz不等式，τ∈[0,4)和w=(w1;w2)∈Kn得，

性质1设φτ、ψ分别由式(3)、(4)定义，则

1)φτ(x,y)为二阶锥权互补函数。

2)对任意(x,y)∈Rn×Rn，有ψ(x,y)≥0。

3)设h=(h1;h2)由式(6)～(8)定义，令

(z1;z2)∈R×Rn-1，

(10)

则ψ在Rn×Rn上处处光滑，且

b)若(x,y)≠(0,0)，h∈intKn，则

c)若(x,y)≠(0,0)，h∉intKn，则

(11)

证明1)要证φτ(x,y)是二阶锥权互补函数，即证

⟹假设φτ(x,y)=0，则

(x+y)=0。

2)由ψ(x,y)的定义可证。

3)先证ψ在Rn×Rn上处处可微。由文献[9]引理3.1知，ψ在任意点(x,y)∈Rn×Rn处处可微。

a)若(x,y)=(0,0)，则

b)若(x,y)≠(0,0)，h∉intKn，易证

(12)

设λ1(h)、λ2(h)是h的谱值，由定义1得，

(13)

则由式(10)、(12)、(13)可得，

(14)

(15)

其中，

若h2≠0，

c)由文献[8]类似可证式(11)。

当(a,b)=(0,0)或

φτ(x,y)。

(16)

因为υ∉intKn，所以由式(11)得

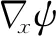
φτ(a,b)=

φτ(a,b)。

(17)

又由引理1和文献[8]的证明可得，

(18)

所以由式(16)～(18)可知，当(x,y)→(a,b)时，

定理1设φτ、ψ分别由式(3)、(4)定义，对任意(x,y)∈Rn×Rn，有

当且仅当φτ(x,y)=0时，等式成立。

类似文献[1]可证，证明省略。

3 下降算法及数值算例

推广CP的下降算法[9]求解式(1)，并给出数值算例。

f(ζk+ρmdk(ζk,γm))≤f(ζk)-

(19)

成立的非负整数m的最小值mk,其中σ,ρ,γ∈(0,1)，

式(19)无需通过求F的导数计算搜索方向和步长，减少了算法的工作量。由文献[9]可知，当F单调时，总存在γm∈[0,1)，使得dk(ζk)满足下降条件式(19)。

选取参数ρ=0.35,γ=0.5,σ=0.15，随机生成矩阵N∈Rn×n及向量q∈Rn。令M=NTN，每次实验均随机生成10个线性WSOCCP：

运用下降算法进行求解。令ζ0=(1,0,…,0)T，τ=1.5,w=(1,0,…,0)T，得到下降算法求解不同规模WSOCCPs的数值结果，如表1所示；令τ=1,w=(1,0,…,0)T，n=100，得到下降算法求解不同初始点WSOCCP的数值结果，如表2所示，其中AObj为ψ(ζ,F(ζ))的平均值，ACPU、AIter分别为算法终止迭代时的平均CPU运行时间和平均迭代次数。从表1、2可看出，下降算法能有效地求解WSOCCP。