基于Copula方法的Lee-Carter模型的长寿互换风险定价研究

胡 月,陈岚岚,章迪平

(浙江科技学院 理学院,杭州 310023)

随着人们生活质量的提高,世界各国人均寿命得以延长,但由此引发的长寿风险日趋严峻。对此,研究者们提出长寿风险证券化,即将长寿风险转移至资本市场。在设计长寿风险证券化产品的过程中,主要面临的问题有死亡率模型的确定及长寿风险证券化产品的运行机制及定价。预测死亡率是有效管理长寿风险的基础,由于传统的静态死亡率模型未考虑到死亡率与时间的变化关系,不适用于死亡率的预测,因此研究者们提出了动态死亡率模型。其中,Lee和Carter提出了Lee-Carter模型[1],该模型被美国统计局用于美国的长期死亡率预测。在此基础上,国内外研究者们对其进行扩展和改进。Renshaw等[2]引入出生年效应;Russolillo[3]将Lee-Carter模型中的趋势项增加了时间、年龄与人群三因素;Kleinow[4]用主成分分析法估计不同人群的共同年龄效应,建立了共同年龄效应(common age effect,CAE)模型;Enchev[5]对比了CAE模型和Lee-Carter模型的预测效果,发现CAE模型效果较好;吴晓坤等[6]对模型参数再抽样,优化Lee-Carter模型的预测效果;赵明等[7]以中国为例,将不同阶段人口死亡率的变动特征,引入Lee-Carter模型;柳向东等[8]考虑不同地区之间死亡率的长期均衡关系,建立了误差修正模型预测Lee-Carter模型中的趋势项;王志刚等[9]假设男女死亡率线性相关,引入Lee-Carter模型,并对中国人口死亡率进行预测;王志刚等[10]建立了具有相关性的多总体Lee-Carter模型;赵明等[11]对比了多人口Lee-Carter模型的效果,发现多人口率模型在稳健性方面表现更好。

长寿风险产品定价主要有风险中性定价法[12]、单因素Wang转换法[13]、双因素Wang转换法[14]和Sharpe比率定价法[15]。樊毅等[16]应用双因素Wang转换法对长寿债券进行定价;由于风险中性定价法的风险中性测度较难确定,胡仕强等[17]提出用最大熵方法来确定风险中性测度;宋平凡等[18]提出用相对熵方法确定风险中性测度;Liu等[19]考虑了投资组合的敏感性和隐藏状态的负债提出了广义状态-空间对冲方法;田玲等[20]提出运用风险立方模型对长寿债券进行定价;杨刚等[21]提出利用百分位分层定价法对逆生存债券进行定价。在实践应用中的定价方法主要有Wang转换定价法和Sharpe定价法。相比Wang转换定价法,Sharpe比率定价法计算更简便。

目前,关于具有非线性相依的长寿互换产品研究较少,而忽视这种相依性将会对长寿风险衍生产品的定价造成不可忽视的影响。因此,本文基于经典的Lee-Carter模型,深入挖掘中国男女群体之间死亡率的相依关系,建立改进的Lee-Carter模型,并给出Sharpe比率定价法下的长寿互换产品价格。

1 死亡率预测模型的建立

目前,对长寿风险产品定价时往往应用单一群体的死亡率进行定价,对总体死亡率进行定价时则用简单线性相加的方法,当不同群体之间的死亡率是相互独立时,该方法不会出现问题。然而,在现实中,由于同一地区具有相同的社会生活环境,男性与女性之间死亡率的变化进程往往存在相依关系,并且保险公司或养老基金需要转移的长寿风险并不是单一群体的长寿风险,应用单一群体的死亡率替代总体的死亡率会产生基差风险,若进行简单的线性相加会产生风险估计的偏差。因此,在研究中考虑相依性是有必要的。

1.1 二维Lee-Carter模型的建立

对中国男性人口死亡率和女性人口死亡率建立二维Lee-Carter模型:

(1)

(2)

式(2)中:T为观测年数。

1.2 Copula-ARIMA模型的建立

Sklar[22]提出Copula函数理论,Copula函数可以将一个联合分布函数与它们各自的边缘分布函数连接在一起,描述变量之间的相依关系。阿基米德Copula函数族中,最常用的有Frank Copula函数、Gumbel Copula函数和Clayton Copula函数,以二元阿基米德Copula函数为例,其表达式和生成元见表1。

表1 二元阿基米德Copula函数Table 1 Binary Archimedes Copula function

引入二元Copula函数,与差分自回归移动平均(autoregressive intergrated moving average,ARIMA)模型相结合,建立具有相依性的ARIMA(p,d,q)模型:

(3)

1.3 两个模型的比较

由于两个模型对单一群体的假设是相同的,因此对单一群体进行预测时,应用改进的Lee-Carter模型得到的均值和方差与原模型的相等。对总体进行预测时,Lee-Carter模型的假设条件是男女死亡率相互独立,改进的Lee-Carter模型的假设条件是男女死亡率是相依的。

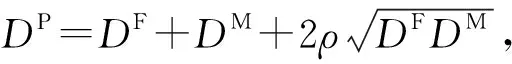
2 长寿互换运行机制及定价

2.1 长寿互换运行机制

长寿互换是交易双方基于目标人群的未来实际死亡率和预期死亡率进行的现金流互换合同。Lin等[23]最早对其进行了理论探索,随后Dowd等[12]提出了每年互换一方以固定现金流交换另一方浮动现金流的普通长寿互换,简称长寿互换。

Coughlan等[24]正式提出q远期合约的概念及设计机制。q远期合约是一种新型的建立在摩根大通公司编制的标准化生命指标基础上的死亡率互换合约,它是普通生存互换的特殊形式。q远期合约的内容如下:约定到期时根据实际死亡率与固定死亡率进行一次现金流互换的协议。图1是q远期合约的运行机制,在期初,约定固定支付为Kt=q′eV,由死亡率模型预先确定,其中q′e=(1+π′)qe为经过风险调整后的预期死亡率,V为面值;浮动支付为St=qfV,由实际死亡率确定,其中qf为实际死亡率,根据摩根大通公司编制的标准化生命指标中的死亡率指数确定。

图1 q远期合约运行机制Fig.1 Operating mechanism of q forwards contract

2.2 Sharpe比率定价法

预先给定一个Sharpe比率S,即风险参数的市场价格,可以对比某项资产的Sharpe比率获得。如果一项资产潜在风险越高或与其他资产相关性越高,那么S越大;若资产流动性越低,则S越大。Sharpe比率公式如下:

(4)

式(4)中:E(R)为年预期收益率;σ为死亡率的同比变化标准差。

预期死亡率加上负风险溢价与预期死亡率的乘积等于实际的死亡率,即(1+π′t)qe=qf,则风险溢价πt=-π′t,结合式(4)可以推导出:

(5)

3 实证分析

3.1 数据说明

本研究利用中国男性与女性人口死亡率数据进行实证分析,数据来源于《1995—2006年中国人口统计年鉴》和《2007—2018年中国人口和就业统计年鉴》。计算男性与女性死亡率的Pearson相关系数,结果为0.97,且p值均小于0.01,通过显著性检验。图2为1994—2017年男女死亡率散点图。由图2可知,男女死亡率的数据集中在零点附近,然后逐渐发散,说明男性与女性群体的死亡率确实存在相依关系。

图2 1994—2017年男女死亡率散点图Fig.2 Scatter plot of male and femalemortality from 1994 to 2017

3.2 参数估计

利用最小二乘法计算出男性女性α、β和k的估计值,如图3～5所示。计算得到αF和αM的Pearson相关系数为0.994,βF和βM的Pearson相关系数为0.605,kF和kM的Pearson相关系数为0.981,且均通过显著性检验。这说明男女死亡率的相关性主要体现在年龄的自然变化规律和时间的进程中。在预测时,由于两个年龄项参数保持不变,因此只需建立具有相依性的时间项参数模型即可,这也说明本研究建立的模型是合理的。

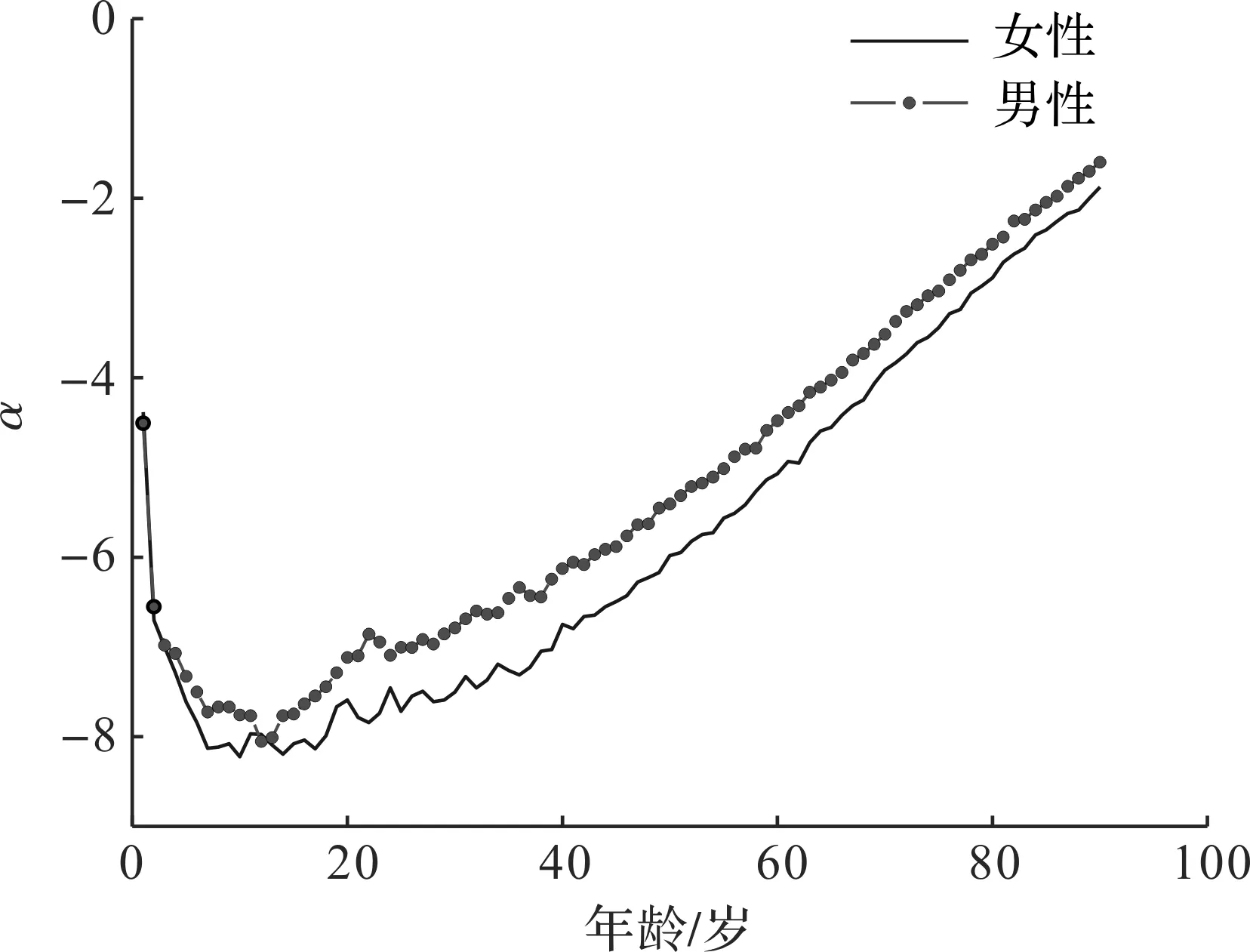
图3 男性与女性的α值Fig.3 α values for men and women

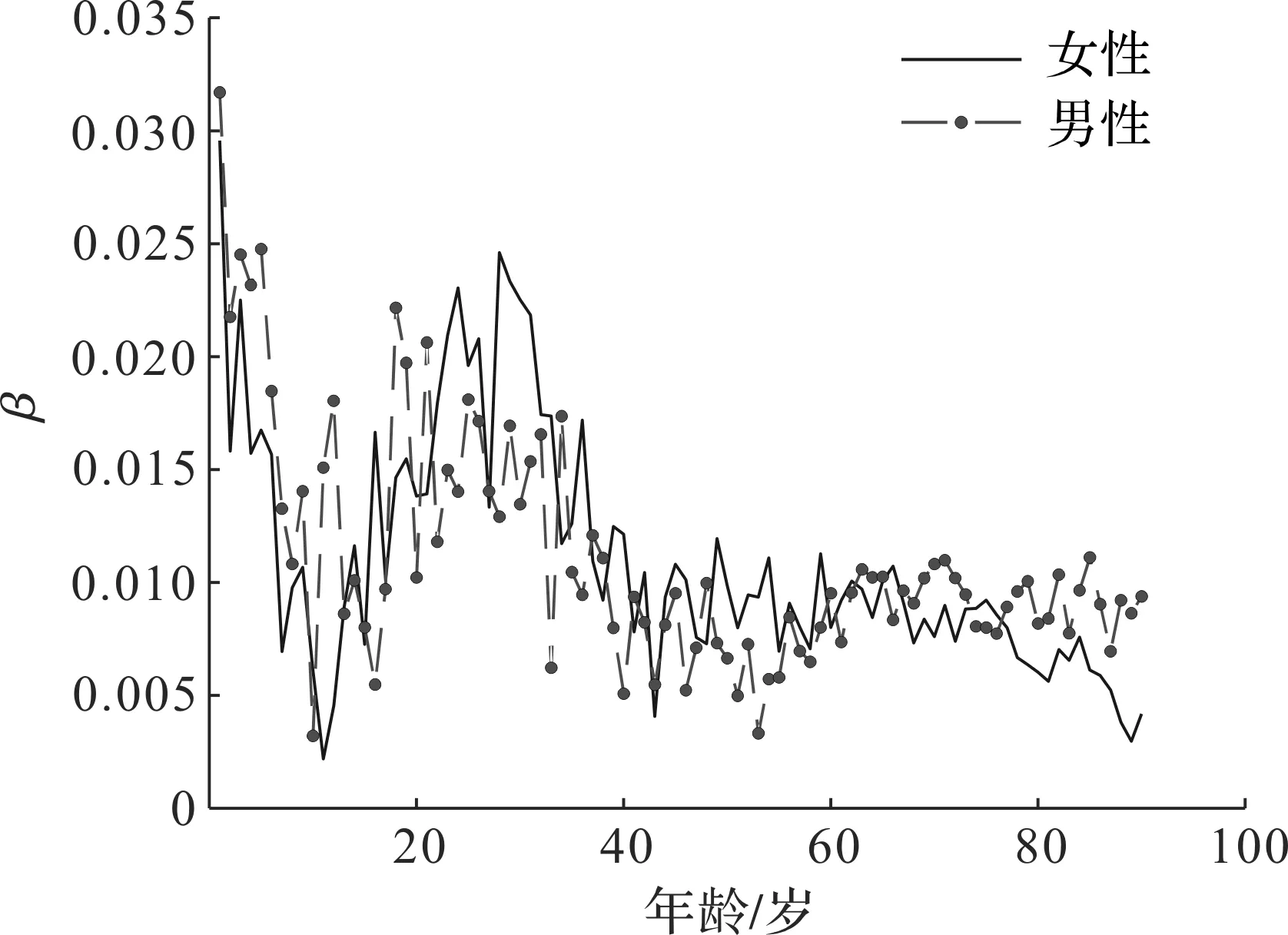
图4 男性与女性的β值Fig.4 β values for men and women

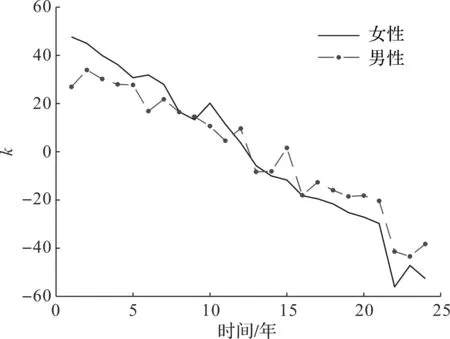
图5 男性与女性的k值Fig.5 k values for men and women

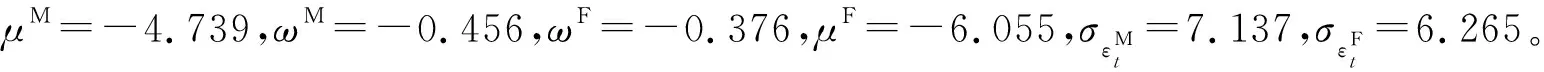
3.3 预测效果

为了检测模型的预测效果,以1994—2013年中国男女人口死亡率的数据,通过蒙特卡罗模拟,计算两个模型在未来5年的死亡率预测值与实际值的均方误差,结果见表2。由表2可知,两个模型中男性的均方误差在0.03以下,女性的均方误差在0.01以下,且两个模型的均方误差十分接近。整体而言,原模型的均方误差相比改进模型的均方误差略小,这是由于我们假设了男女死亡率存在相依性,这对个体的拟合效果有细微的影响。

表2 两个模型未来5年的死亡率预测值与实际值的均方误差Table 2 Mean square error of predicted value and actual value of mortality of two models for next 5 years

3.4 长寿互换定价

根据国务院规定,男职工年满60周岁、女职工年满55周岁退休,养老金的支付时间从退休时开始计算,所以养老基金及保险公司所面临的长寿风险,即60岁男性与55岁女性的长寿风险。

下面以目前60岁男性与55岁女性为例,假设男女人口比例为1∶1,交易双方约定以q远期合约为基础,约定未来30年男性与总体每年进行长寿互换,未来40年女性每年进行长寿互换。约定面值为1,S=0.75。由于较难直接获得死亡率的方差,因此利用蒙特卡罗模拟计算长寿互换价格,步骤如下:

3)由式(1)得到男性、女性及总体n年后的中心死亡率预测模型

(6)

将时间项分别代入式(6)中,得到男性、女性与总体的中心死亡率,再将其转换为死亡率;

4)将1)～3)重复3 000次,再计算男性、女性与总体死亡率的方差;

5)将4)中得到的方差代入式(5)中,并计算q远期合约每年的价格和平均价格。

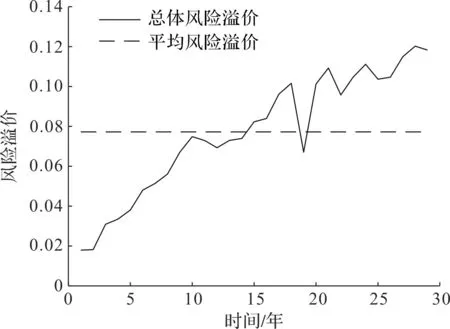
图6 总人口未来30年死亡率风险溢价Fig.6 Mortality risk premium for totalpopulation for next 30 years

根据上述步骤得到总人口未来30年死亡率风险溢价、55岁女性未来35年死亡率风险溢价和60岁男性未来30年死亡率风险溢价,如图6～8所示。目前60岁的男性人口在未来17年内的死亡率风险溢价总体呈上升趋势,略有波动;在未来18年至30年内风险溢价上升趋势相对前17年变缓,但是波动频率变大。女性的风险溢价在未来的20年呈上升趋势,之后在0.10上下波动。

男性的平均风险溢价为0.077 8,女性的平均风险溢价为0.088 4,总体的平均风险溢价为0.077 2,说明在退休之后女性的死亡率不确定性比男性更大。另外,我们计算出女性在未来30年的平均风险溢价为0.082 1,在未来30年内,若通过线性相加的方法得到总体的平均风险溢价,那么它介于男性与女性的平均风险溢价之间;而通过本研究方法,总体的平均风险溢价小于男性与女性的风险溢价。这两种方法有显著的区别,这是由于男性与女性的死亡率存在非线性相依关系,以往的线性相加方法将失效。

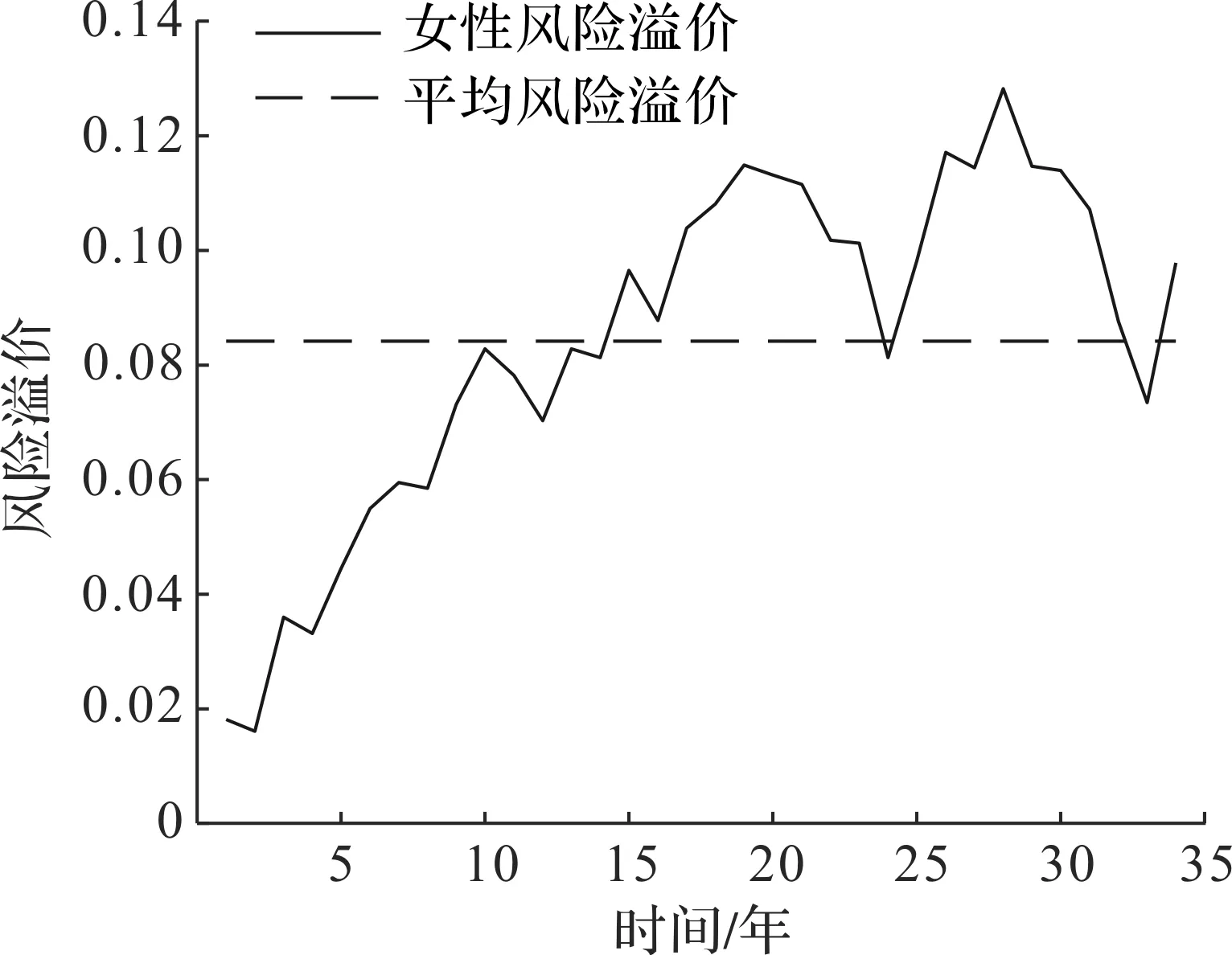
图7 55岁女性未来35年死亡率风险溢价Fig.7 55-year-old female mortality riskpremium for next 35 years

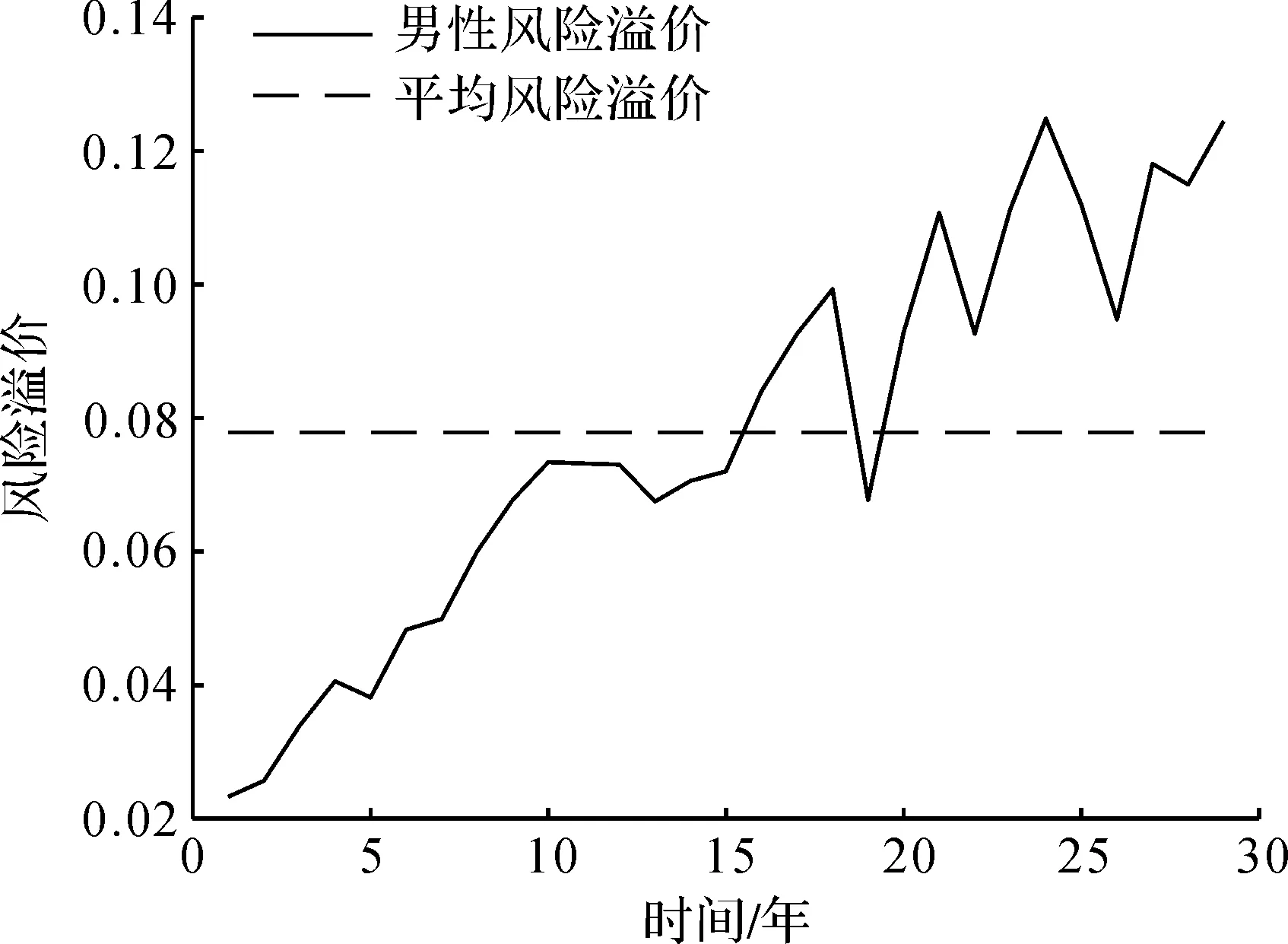
图8 60岁男性未来30年死亡率风险溢价Fig.8 60-year-old male mortality riskpremium for next 30 years

3.5 各因素的影响

为分析不同样本周期长度对风险溢价的影响,以目前65岁人口为例,以1994—2016年为起始时间,2017年为终止时间,其他条件固定,计算不同样本周期下的风险溢价,结果如图9所示。由图9可知,随着周期变长,风险溢价呈波动上升的趋势,由于周期延长,不确定性增加,风险随之增大,风险溢价也随之增大,这是合乎逻辑的。为进一步分析起始年份对风险溢价的影响,以目前65岁人口为例,以1994—2013年为起始时间,计算不同起始时间下的风险溢价,如图10所示。由图10可知,不同起始时间也会对风险溢价造成影响,这种影响具有随机性。另外,根据式(5),可以知道S对风险溢价的影响是呈线性的;当σq确定时,互换周期t对风险溢价的影响也是呈线性的。

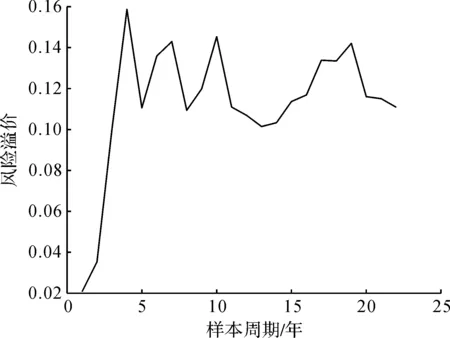
图9 不同样本周期下的风险溢价Fig.9 Risk premium under different sample periods

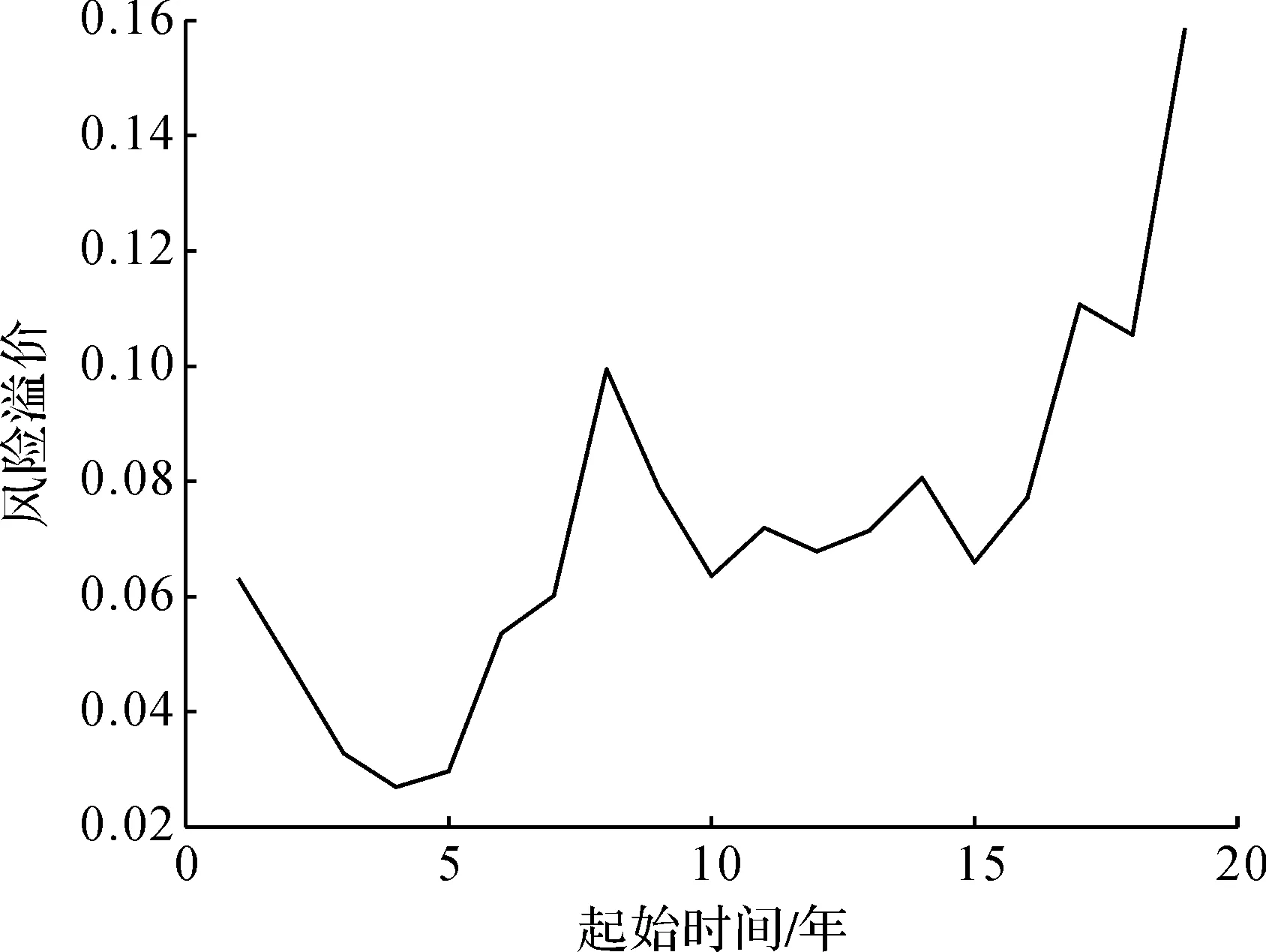
图10 不同起始时间下的风险溢价Fig.10 Risk premium at different starting times

4 结 语

为实现长寿风险证券化,本研究联系实际,建立了具有相依性的Lee-Carter模型,并应用Sharpe比率定价法对长寿互换定价。在实证分析中更清楚地说明男女死亡率在时间变换进程中的相依关系是事实存在的,对长寿风险定价的影响是显著的。因此,对模型进行Copula分析是必要的。同时,本研究也为长寿互换产品的合理定价提供了参考。在此基础上,分析了样本周期、样本的起始时间、Sharpe比率和长寿互换的期限对长寿互换价格的影响,发现各因素的影响都是显著的,说明应用Sharpe比率定价法对长寿互换定价是有效的。在未来,长寿互换产品必将成为连接资本市场与保险市场的重要纽带,该研究可为建立起长寿风险证券化市场提供参考。因此,本研究具有一定的理论价值与现实意义。在未来,我们将进一步研究中国长寿风险市场下Sharpe比率的取值,以推进Sharpe比率定价模型在中国长寿风险市场的应用。