基于多维特征融合的鲁棒频谱感知技术

母诗源 王晓庆

(中国电子科技集团公司第五十四研究所，河北石家庄 050081)

0 引言

无线通信技术的迅猛发展使得有限的频谱资源更加稀缺，然而频谱利用率相对有限。频谱感知作为认知无线电的一项关键技术，让用户机会性地使用空闲频谱来提高频谱利用率。

目前主流的频谱感知方法，具有不同的适用场景及优缺点。能量检测通过对信号的能量值与阈值进行判别，对于未知的多径散射信道具有鲁棒性，实现简单且可实现盲感知，但容易受不确定性噪声的影响，在低信噪比下感知性能衰减严重[1]。匹配滤波器检测方法能在短时间内得到最大的信噪比进行判别，适用于已知先验信息的场景，然而检测性能受载波频率偏移和相位噪声影响较大[2]。循环平稳特征检测在低信噪比条件下具有较高的检测性能，但需要准确知道授权用户的循环频率，同时计算复杂度较高。特征值检测基于接收信号的协方差矩阵，构建检验统计量，具有很好的抗干扰能力，然而依赖精确的同步信息和先验信息，且复杂度较高。

近年来，通过多天线频谱感知方法对抗噪声不确定性的恶劣影响，可使频谱感知性能得以改善[3]。文中提出一种新的频谱感知方法(MARE)，对噪声不确定性具有鲁棒性。该方法中，不需要授权用户传输信号、从授权用户到认知用户的衰落信道以及噪声方差的任何先验知识，仅通过样本协方差矩阵的多维特征值来提取信号丰富的特征，获得更好的感知性能。

1 系统模型

认知用户接收器配备有M根天线，每根天线在一个感应周期内收集N个样本。假设H0表示PU信道无信号的情况，H1表示授权用户信道存在信号的情况。两种假设下的接收信号样本分别给出如下：

其中，w(n)=[w1(n)，…，wM(n)]T为M×1的圆对称复高斯(CSCG)噪声矢量，并遵循分布；h=[h1，…，hM]T表示从授权用户发射器到认知用户接收器的平坦衰落信道，假设信道在每个检测周期中都是一个不变的参数；s(n)是授权用户的发送信号。认知用户处的接收样本矩阵表示为X=[x(1)，…，x(N)]。

2 天线MARE检测方法

2.1 MARE检测方法

认知用户接收器收到信号后，定义接收信号的统计协方差矩阵为：

其中Es表示授权用户发送信号的功率，(·)H表示自共轭矩阵转置。令Rx和hhH的有序特征值分别为λ1>…>λM和μ1>…>μM。如果授权用户信道是空闲的，i=1，…，M；如果授权用户信号是存在的，根据有序特征值来检测授权用户信号是否存在，但由于只有有限数量的样本信号，无法统计协方差矩阵。于是，采用样本协方差矩阵来近似代表统计协方差矩阵，将其定义为：

针对样本协方差矩阵，提出MARE检测算法，概括为以下四个步骤：

步骤1：求出在公式(3)中定义的样本协方差矩阵；

步骤2：求出样本协方差矩阵的有序特征值；

步骤3：生成检测统计量：

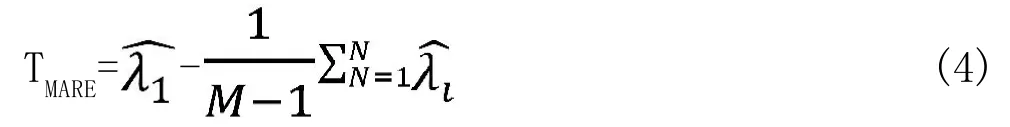
步骤4：将检测统计量与门限值比较，如果检测统计量大于门限值，认为授权用户信号是存在的；否则，认为授权用户信号是不存在的。判决公式为：

从公式(4)可以看出，检测统计量是样本协方差矩阵的最大特征值与其余特征值的平均值之差，MARE检测方法不需要噪声方差的先验知识，因此对噪声不确定性具有鲁棒性。

2.2 假说H0下随机变量的矩

在此计算随机变量的矩，检测统计量能被扩展为：

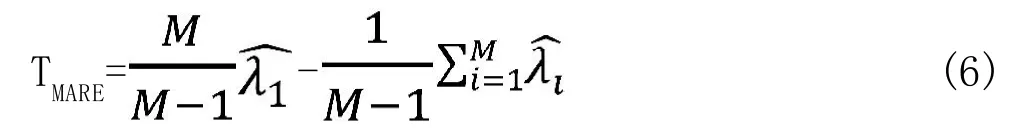
由公式(6)可以看出，检测统计量可以分为两部分，分别是最大特征值及样本协方差矩阵的有序特征值。首先计算最大特征值的矩，授权用户没有传输信号时：

定义1：定义m*n的矩阵A，矩阵A的列向量表示协方差矩阵的零均值独立实数/复数高斯向量。m×m随机矩阵W=AAH是一个具有n个自由度和协方差矩阵Σ(服从W～CWm(n，Σ)分布的中心复威希特Wishart矩阵)。

其中KUC=[ (N-i)! (M-j)!]-1；φ(p)在公式(9)中被定义：

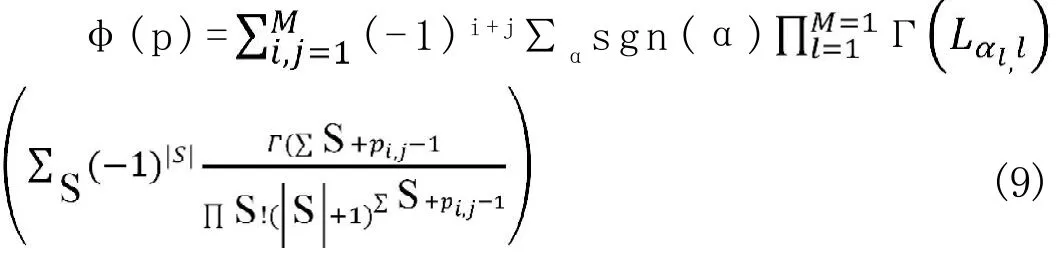
sgn(·)是正负号函数；αl是{1，2，…，M-1}排列的第l个元素由下式确定：

此外，S是集合{l1，l2，…，lL-1}的子集，|S|是S的基数，∑S是中所有元素的总和，∏S!是S中每个元素分解的乘积。将p=1和p=2代入(8)，可以在假设H0下获得的一阶矩和二阶矩。接下来，计算样本协方差矩阵的迹的一阶矩和二阶矩。在假说H0的情景下认为：

其中rii表示样本协方差矩阵的对角元素；wi(n)代表噪声向量w(n)的元素。噪声向量w(n)的元素是随机变量。

接收样本协方差矩阵的迹服从中心卡方分布，得出结论：

2.3 判决阈值和误检概率

在此利用高斯分布来近似检验统计量的分布，得到一阶矩和二阶矩适合的参数。

假说H0的情况下，检测统计量TMARE的高斯概率分布函数为：

其中：

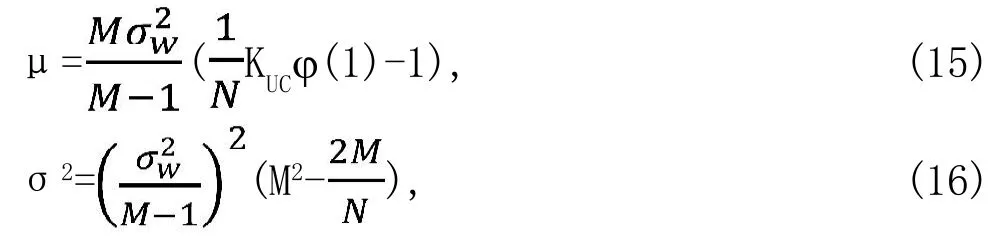
其中：

Ψ=(1/N)2{KUCφ(2)-KUCφ(1)}2

误检概率Pfa为检测到授权用户的信号，但实际上不存在授权用户信号。由公式(14)可得误检概率Pfa为：

其中Q(·)是互补累积分布函数(CCDF)，i.e.，标准高斯分布的右尾概率。

通常希望将误检概率Pfa控制在某个常数ε下，同时将检测概率Pd(即奈曼-皮尔逊(NP)准则)最大化。计算判决阈值：

其中ε是理想误检概率，Q-1(·)是Q(·)的反函数。

3 仿真结果

图1 多种检测方法检测概率及接收机工作特性曲线

图2 噪声不确定条件下,检测概率随信噪比变化的关系曲线

在仿真中假设授权用户发送器发送独立的BPSK信号，将所提出的信号检测方法(MARE)和现有的检测方法进行了比较。

图1中，可以看出MARE方法的检测性能优于EME 3dB。与B-GLRT和AGM方法相比，MARE算法均具备更优的检测性能，其检测统计量是最大特征值与样本协方差矩阵的其余特征值的平均值的加权组合，而B-GLRT和AGM的检测统计量都是特征值的简单组合。

图2中，可以看出在没有噪声不确定性的情况下，MED方法效果更好。而在考虑噪声不确定性的影响时，MED的检测概率Pd严重下降，MARE仍可以很好地工作。不管有无噪声不确定性情况下，MARE的三条曲线几乎重叠，验证了相关的分析。

4 结论

在本文中，提出了一种基于多维特征融合的鲁棒频谱感知的技术，该方法利用了在认知用户接收器处从每个天线接收信号之间的相关性。该方案对噪声不确定性具有鲁棒性，并且具备优异的检测性能。