Plasmonic characteristics of suspended graphene-coated wedge porous silicon nanowires with Ag partition*

Xu Wang(王旭), Jue Wang(王珏), Tao Ma(马涛),2,†, Heng Liu(刘恒),3, and Fang Wang(王芳),2

1College of Electronic and Electrical Engineering,Henan Normal University,Xinxiang 453007,China

2Henan Key Laboratory of Optoelectronic Sensing Integrated Application,Xinxiang 453007,China

3Academician Workstation of Electromagnetic Wave Engineering of Henan Province,Xinxiang 453007,China

Keywords: surface plasmon polariton,graphene,porous silicon,finite element method(FEM)

1. Introduction

Graphene is an atom-thick monolayer two-dimensional(2D) carbon material in which the atoms are arranged in a honeycomb lattice.[1–4]It has remarkable optical properties,such as broadband absorption, tunable Fermi level, and large nonlinearity.[5–8]In the mid-infrared band and THz band,graphene exhibits a strong semi-metal property and supports surface plasmon polariton(SPP).[9–12]Graphene has a strong interaction with light in a wide frequency range and is suitable for active applications. In last decades, different structures based on graphene have been widely reported, such as graphene arrays,[13–15]graphene nano-ribbons,[16]dielectricloaded graphene plasmon waveguide,[17,18]dual-grapheneon-graphene configuration,[19]and multilayer graphene metamaterial.[20]Comparing with the traditional noble metal materials, graphene-based SPP waveguides can achieve high optical performances and low propagation loss.[21]

Recently, the graphene-coated nanowire waveguides(GCNWs) based on graphene SPP have been proposed,which have better performances including the small loss and high mode field confinement than the conventional dielectric waveguides. A semiconductor-graphene cylinder was investigated to be applied to the transmission of THz waves with a weak effect of light wave broadening in the remote transmission.[22]A GCNW based on an elliptic cylinder instead of a cylinder was investigated to achieve a large propagation length of ～200 μm with a small normalized mode area of ～10-3.[23]A coaxial-like GCNW-based long-range SPP waveguide was designed, which is composed of a cylindrical silicon nanowire core surrounded by an inner graphene layer,a silica layer,and an outer graphene layer from inside to outside.[24]The simulation results showed that an ultrasmall normalized mode area of ～10-5with a propagation length of～8 μm can be achieved at an operating wavelength of 7 μm.The Sommerfeld wave in a single-wire THz waveguide is radially polarized,difficult to excite,and weakly guided,which limits the practical applications of the THz waveguide. To solve the problem, a two-wire terahertz waveguide was proposed,which has lower bending loss than the single-wire THz waveguide.[25]In order to improve the performances of the GCNW,a thin low-index buffer layer was embedded between the GCNW and substrate.[26]It was found that a low propagation loss of 0.312 dB·μm-1with an improved figure of merit(FoM) can be realized when an ultra-small buffer thickness and gap distance are chosen. In addition, two vertically coupling cylindrical GCNWs integrated with a thin high-index dielectric substate are also studied to improve the performances of the GCNW.[27]The results show that the proposed suspended wedge GCNW’s FoM is nearly two-fold higher than that of the plasmon mode in the single GCNW on a substrate.

Due to the good optical properties, porous silicon (PS)is a suitable candidate for the applications of optoelectronics such as in light-emitting diodes,photodetectors,optical modulators, and optical sensors.[28–32]The large internal surface of PS can enhance the interaction between light and matter.The tunable porosity of PS, which varies with the fabrication parameters,[30]makes its refractive index (RI) vary between the air and the bulk silicon. Moreover,the hybrid structures combining PS with graphene-based materials proved to be helpful in the applications in photonic and energy conversion devices.[33,34]The hybrid PS/graphene-based structures provide a great platform for their applications in optoelectronics,power engineering,and sensing.[31]

In this paper, a GCNW composed of two suspended graphene-coated wedge PS nanowires with an Ag partition is designed. The plasmonic characteristics and sensing performances of the SPP mode in the designed structure are investigated by using the finite element method(FEM).By sweeping the geometry parameters,the plasmonic characteristics of the suspended wedge GCNW are optimized. To evaluate the sensing performances,the waveguide sensitivity is calculated.The plasmonic characteristics and sensing performances are compared with their counterparts of other different GCNWs.The rest of this paper is organized as follows. In Section 2,the structure of the proposed suspended wedge GCNW is designed.In Section 3,the plasmonic characteristics and sensing performances are analyzed and optimized. Conclusions and perspectives are drawn in Section 4.

2. Waveguide structure

Figure 1 shows the schematic of the suspended wedge GCNW composed of two isosceles triangular nanowires coated with graphene symmetrically distributed on both sides of an Ag partition. The thickness of the Ag slab is denoted as t. The three apex angles for each of the wedge dielectric nanowires are chamfered with corner radius r being 25 nm.The height and the apex angle of the triangle are denoted as L and θ, respectively. The gap between the apex angle of the triangular nanowire and the Ag slab is marked as g.The RI of porous silicon is ～1.55.[32]The dielectric constant of the monolayer graphene can be calculated from εg=1+iσg/(ε0ωtg),[35]where tgis the thickness of the monolayer graphene,ω is the angular frequency of the incident light,and ε0is the permittivity in free space. Within the random phase approximation,the dynamic optical response of graphene can be derived from the Kubo’s formula,[36]σg=σintra+σinter,where σintraand σinterare the intra band contribution and inter band contribution, respectively. In the terahertz band and the infrared band,the surface conductivity of graphene can be approximated as[37]

where τ is the relaxation time, T is the ambient temperature,EFis the Fermi energy,hbis the reduced plank constant,kbis the Boltzmann constant, and e=1.6×10-19C. Here,T =300 K,and τ =0.5 ps.

Fig.1. Schematic diagram of suspended wedge GCNW.

The dielectric constant of Ag is described by Drude–Lorentz model[21]

The mode characteristic, propagation performance and sensing performance of the suspended wedge GCNW are simulated by the commercial software COMSOL Multiphysics based on the FEM which is widely used to calculate the characteristics of integrated photonic devices. The computational domain is discretized into triangular meshes. The scattering boundary condition is used in the simulations. The mesh grid in graphene layer is refined to ensure the accuracy of calculation. Convergence test are done to ensure that the calculation region and mesh size do not interfere with the results.

3. Plasmonic characteristics

3.1. Mode field distributions

The mode field distributions of the modes in the suspended wedge GCNW are shown in Figs. 2(a)–2(c). The results show that the SPP mode is a fundamental mode in the suspended wedge GCNW.The mode energy of the SPP mode is mainly distributed between the porous silicon and Ag partition. However, the guide mode in the porous silicon is restricted due to the small cross-section size of the proposed GCNW (200 nm). Here, L=200 nm,t =40 nm, g=5 nm,and EF=0.5 eV.The normalized electric field(E)along the x direction(y=0)and along the y direction(x=t/2+g/2)of the suspended wedge GCNW are shown in Figs.2(d)–2(f)and Figs.2(g)–2(i),respectively. The normalized E in x direction has a maximum value at the graphene surface due to the SPP effect.

Fig.2. Mode field distributions of suspended wedge GCNW with(a)g=5 nm,(b)10 nm,and(c)20 nm;normalized E along x direction across(y=0),(d)g=5 nm, (e)g=10 nm, and(f)g=20 nm; normalized E along y direction across(x=t/2+g/2), (g)g=5 nm, (h)0 nm, and(i)20 nm, with other parameters being EF=0.5 eV,T =300 K,τ =0.5 ps,L=200 nm,t=40 nm,and nc=1.0.

3.2. Mode characteristics

Generally,the mode characteristics are highly dependent on the geometry parameters of the waveguide. The geometry parameters effect on the mode characteristics including Re(neff), Lp, Am, and FoM are investigated when the operating frequency f0is 30, 40, and 50 THz, separately. Here,EF=0.6 eV,L=200 nm,r=25 nm,θ =60◦,and nc=1.0.The influences of g on Re(neff), Lp, Am, and FoM with different frequencies are shown in Figs.3(a)–3(d). As shown in Fig.3(a),Re(neff)decreases with g rising because the coupling between the graphene-coated nanowire and the slab substrate is weakened. In Fig.3(b), Lpfirst increases slightly and then decreases slowly as g increases. As g increases from a small value, the influence of the ohm loss in Ag slab reduces Lp.When g keeps growing, the mode confinement weakens and Lpdecreases. As shown in Fig.3(c),an increasing g will dramatically reduce Am. It indicates that the suspended wedge GCNW has better mode confinement when g is small. As shows in Fig.3(d),a smaller g matches a better FoM.As shown in Figs. 3(a)–3(d), the operating frequency has a great influence on the mode characteristics. The high frequency leads to a large Re(neff)and Am, but a short Lp. The GCNW has a better FoM at the high frequency when g is less than 10 nm.Considering the tradeoff between Lpand FoM,g is chosen to be 10 nm.

The effects of L on the mode characteristics of the suspended wedge GCNW are shown in Figs. 4(a)–4(d). The increasing of L lead Re(neff)and Lpto slightly increase while Amincreases significantly at a higher operating frequency. Meanwhile, a higher operating frequency corresponds to a smaller Lpand a larger Am. In Figs.5(a)–5(d), the mode characteristics have no decisive dependence on t. As is well known,the mode energy of the SPP mode is mainly distributed at the interface between the dielectric and metal. There is almost no distribution inside the metal(Ag). This can be proved by the mode distributions which have been shown in Figs.2(a)–2(c).Hence, the thickness of the metal (t) has little effect on the mode characteristics.When f0increases,the larger absorption of graphene leads the propagation loss to increase, which reduces Lp. However, Amincreases with frequency increasing.The mode characteristics of the GCNW are not sensitive to t,which implies that the suspended wedge GCNW has a good tolerance to the fabrication error. In the following simulations,t is chosen to be 40 nm.

Fig.3. Influences of g on(a)Re(neff),(b)Lp,(c)Am,and(d)FoM at f0=30 THz,40 THz,and 50 THz.

Fig.4. The L-dependent(a)Re(neff),(b)Lp,(c)Am,and(d)FoM for f0=30 THz,40 THz,and 50 THz.

Fig.5. Influences of t on(a)Re(neff),(b)Lp,(c)Am,and(d)FoM for f0=30,40,and 50 THz.

According to Eq. (1), σgcan be flexibly tuned through varying EFwhich can be electrically controlled by the bias voltage supplied to the monolayer graphene. To demonstrate the tunability of the suspended wedge GCNW,the mode characteristics as a function of EFare shown in Figs.6(a)–6(d). As shown in Fig.6(a),Re(neff)decreases with EFincreasing,but increases with f0increasing. In Fig.6(b),Lpincreases monotonically with EFincreasing,but decreases with f0increasing.The inter band loss of graphene serving as a dominant factor is low at a large EF,which results in the increase of Lp. Furthermore, the increase of EFwill lead the value of τ to increase,which can further reduce the loss and increase Lp. In Fig.6(c),Amfirst increases and then decreases when EFchanges from 0.2 eV to 0.9 eV, and has a maximum when EF=～0.41 eV due to the smallest permittivity of the graphene. The dependence of FoM on EFis shown in Fig.6(d),which indicates that the overall performance of the suspended wedge GCNW can be improved when EFincreases.

Fig.6. EF-dependent(a)Re(neff),(b)Lp,(c)Am,and(d)FoM for f0=30,40,and 50 THz.

Fig.7. Effects of nc on(a)Re(neff),(b)Lp,(c)Am,and(d)FoM for f0=30,40,and 50 THz.

For the applications in sensing,the effects of the cladding RI(nc)on the mode characteristics are investigated. The valuations of Re(neff),Lp,Am,and FoM with ncin a range from 1.0 to 1.9 are shown in Figs.7(a)–7(d)at different values of f0.Here, we take r=20 nm, L=200 nm, g=10 nm, θ =60◦,and EF=0.6 eV. As shown in Fig. 7(a), Re(neff) increases with the ncincreasing monotonically. The changes of Re(neff)show a near-linearly increasing trend which can be used as the homogeneous sensing. The waveguide sensitivity (Swg)can be calculated by the linear fitting, which is defined as Swg=Δneff/Δnc.[44]The results show that a larger Swgcan be achieved when f0is higher. As shown in Figs.7(b)and 7(c),both the Lpand Amdecrease with the ncincreasing due to the decrease of the RI difference between the core and cladding.In Fig. 7(d), the FoM is improved when ncincrease from 1,and then tends to be constant when ncis larger than 1.45.

3.3. Comparisons among different GCNWs

In order to compare the mode characteristics and sensing performances among different kinds of waveguides,three different GCNWs are investigated. The three GCNWs are respectively the suspended wedge GCNW, cylindrical GCNW,and isolated GCNW with the same materials. The schematics of the three GCNWs are shown in Figs.8(a)–8(c),respectively.Here, we take L=2R, and the other parameters are the same as those used in the previous simulations. The electrical field distributions of the three waveguides are shown in Figs.8(d)–8(f). The results show that the suspended wedge GCNW and cylindrical GCNW have much higher field confinements than the isolated GCNW.However,the electric field of the mode in the isolated GCNW is mainly concentrated at the interface of the cylindrical nanowire. The electric field distributions of the three GCNW along the x axis are shown in Figs.8(g)–8(i).

Figures 9(a)and 9(b)show the plots of Lpversus Amfor the three GCNWs with different values of f0and nc.As shown in Fig. 9(a), the Lpdecreases but the Amincreases as the f0increases from 10 THz to 50 THz. The suspended wedge GCNW has a longer Lpthan the other two GCNWs at the same value of Am. In Fig.9(b),considering the tradeoff between Lpand Am,the performances of the suspended wedge GCNW and cylindrical GCNW are much better than those of the isolated GCNW as the ncincreases from 1.0 THz to 1.9 THz. The suspended wedge GCNW has more superior performances than the other two. The variations of Re(neff)with the increase of ncfor the three waveguides are shown in Fig. 9(c). According to the linear fitting,the waveguide sensitivities of the three waveguides can be achieved. The results show that the waveguide sensitivity of the suspended GCNW is higher than that of the isolated GCNW, but lower than that of the cylindrical GCNW.

Fig. 8. Schematics of (a) wedge GCNW, (b) cylindrical GCNW, and (c) isolated GCNW; mode field distributions in panel (a) wedge GCNW, (b)cylindrical GCNW,and(c)isolated GCNW;normalized electric field E along x direction(y=0)in(a)wedge GCNW,(b)cylindrical GCNW,and(c)isolated GCNW.

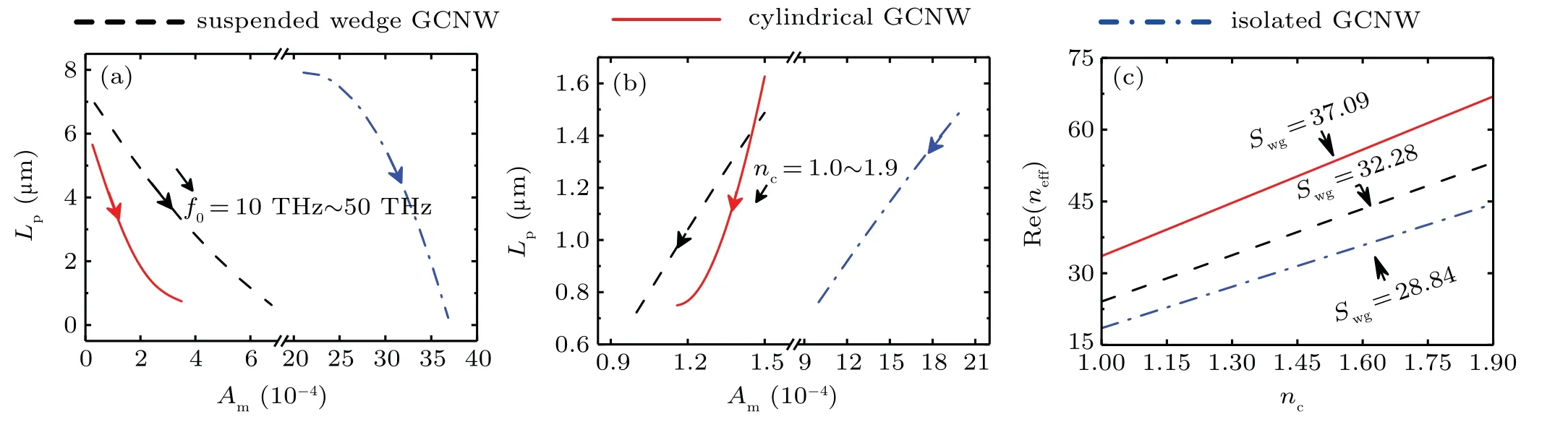
Fig. 9. Comparisons among different GCNWs with different parameters, (a) Lp versus Am for different values of f0, (b) Lp versus Am for different values of nc,and(c)Re(neff)versus nc.

4. Conclusions and perspectives

In this work, a suspended wedge GCNW with a thin Ag partition is investigated. The simulation results show that a normalized mode field area of ～10-4and a figure of merit of ～100 can be achieved by optimizing the parameters. The suspended wedge GCNW has a strong interaction between the metal slab and the nanowires, which can have potential applications in the high-density integrated photonic circuits and optoelectronic devices in terahertz frequency band. The plasmonic characteristics can be dynamically adjusted by changing the Fermi energy of graphene which is tuned by a bias voltage. The suspended wedge GCNW has a relatively high waveguide sensitivity, which has potential applications in RI sensing. The suspended structure and large internal surface of the suspended wedge GCNW can improve its sensing performances. The suspended wedge GCNW has promising applications in the electro-optic modulations,optical interconnects,optical switches,and optical sensing.