锆合金辐照蠕变和生长的宏介观模型研究进展

马慧彤，刘桂森，崔严光，赵冠楠，沈 耀,*

(1.上海交通大学 材料科学与工程学院，上海 200240；2.上海核工程研究设计院，上海 200233)

反应堆燃料组件是反应堆堆芯的核心部件，其尺寸稳定性直接关系到核反应堆运行的安全性和经济性。在反应堆运行过程中，燃料组件所处的工作条件十分苛刻，它不仅受到强烈的中子辐照，还会受到高温高速冷却剂流的侵蚀以及热和机械应力的作用[1]。锆合金因具有低热中子吸收截面、较好的力学性能及高温抗氧化、抗腐蚀能力，已成为反应堆堆芯燃料组件的主要结构材料，如压水堆用燃料包壳管(Zr-2、Zr-4、M5、Zirlo等)及重水堆用压力管(Zr-2.5Nb)等[2]。由于堆内服役环境严苛，锆合金构件在服役过程中不仅会被氧化、腐蚀，更重要的是会辐照变形，这将严重影响其使用可靠性。预测锆合金的堆内变形行为对评估其安全使用寿命、提供事故下的安全裕量具有重要意义，对开发核燃料预测系统具有重要价值。

锆合金的辐照变形主要由材料在高温、辐照、应力作用下缺陷(包括辐照缺陷和晶体固有缺陷)之间的相互作用及演化引起[3-5]，包括热蠕变、辐照蠕变及辐照生长。辐照生长指各向异性材料在无外加应力作用下，辐照时发生的体积守恒的变形，是由辐照产生的点缺陷及其团簇与金属中各向异性阱(位错、位错环及晶界)的择优相互作用引起的[6-8]。蠕变则是在外加应力低于屈服应力时发生的缓慢塑性变形行为。热蠕变是指高温下，没有辐照作用时材料的蠕变行为。辐照蠕变则是在辐照作用下，材料内部产生的大量点缺陷促进位错的运动，导致的热蠕变基础上的额外蠕变增量[9]。这3种变形的叠加导致锆合金构件产生了宏观尺寸和形状的改变。

近年来，国外有很多综述总结了锆合金的辐照变形行为和影响因素，以及相关变形机制的研究进展，但很少有文献直接立足于其辐照变形的预测模型，国内更是缺乏相关的研究报道[9-12]。本文拟分别从宏介观尺度详细综述两类锆合金构件的辐照变形预测模型。针对包壳管的模型有宏观经验模型及介观力学模型。经验模型基于堆内蠕变和生长数据，描述蠕变和生长应变与环境参量(应力、温度、中子注量)之间的经验关系，是当前应用在压水堆包壳管设计及安全许可分析中的主要模型，但其特定的经验参数值只适用于具有特定材料特性并处于特定服役环境下的锆合金。鉴于经验模型的局限性，最新发展起来的介观力学模型变得尤为重要。介观力学模型基于锆合金辐照变形的物理机制，在微观尺度考虑辐照过程中微观结构的演化，在介观尺度通过粘塑性自洽(VPSC)程序考虑织构、晶粒尺寸及形状对辐照变形的影响，模型具有广泛适用性。针对压力管，主要是宏观经验模型，包括C6方程及秦山方程。C6方程考虑了材料的微观结构及织构对辐照变形各向异性的影响，具备一定的物理基础，是当前应用在CANDU重水堆压力管寿命预估中的主要模型，但模型关键各向异性参数及计算方法并未详细公开；秦山方程基于秦山CANDU重水堆压力管辐照变形的统计规律，是一种新的压力管辐照变形预测方程。因此，通过对压水堆用锆合金包壳管及重水堆用Zr-2.5Nb压力管辐照变形预测模型的详细综述，不仅对评估锆合金的辐照蠕变和生长行为具有参考价值，对Zr-2.5Nb压力管国产化研究也具有重要意义。

1 锆合金包壳管的辐照变形预测模型

宏观经验模型及介观力学模型都可用于模拟包壳管的蠕变和生长行为。宏观经验模型基于包壳管热蠕变、辐照蠕变、辐照生长的经验变形规律，通常通过有限元方法求解包壳管变形过程中的力学平衡问题。介观力学模型基于锆合金辐照变形的物理机制，主要通过VPSC程序耦合锆合金热蠕变、辐照蠕变、辐照生长的单晶模型，考虑晶体织构以及晶粒尺寸和形状效应，预测锆合金多晶的蠕变和生长行为。

1.1 包壳管的辐照蠕变和生长行为的基本规律

不同类型的锆合金包壳管的蠕变应变随中子注量变化的曲线示于图1[2]。由于锆合金包壳管织构(Kearns织构因子通常为fr=0.636,ft=0.317,fa=0.047[2]，r、t、a分别代表包壳管的3个宏观特征方向(径向、环向和轴向))，包壳管的环向应变通常只由蠕变贡献，而没有辐照生长的贡献[13]。锆合金的蠕变变形由热蠕变和辐照蠕变组成，但当前测试技术很难将两者分离开来。对不同类型的锆合金，蠕变曲线都可分为初始的瞬态阶段和稳态阶段。初始阶段由于辐照剂量较小、辐照硬化不明显，通常有很高的蠕变率。随着辐照损伤的累积，材料被充分硬化，热蠕变被抑制，蠕变速率逐渐下降至稳定，进入稳态变形阶段。

图1 不同类型锆合金包壳管的辐照蠕变曲线[2]Fig.1 Irradiation creep curves of different types of zirconium alloy cladding tubes[2]

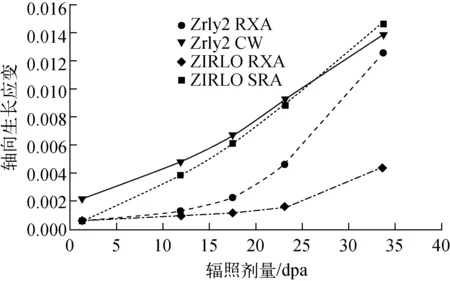
图2 不同类型锆合金包壳管辐照生长曲线[2]Fig.2 Irradiation growth curves of different types of zirconium alloy cladding tubes[2]

不同类型的锆合金包壳管轴向生长应变随辐照剂量(中子注量) 的变化示于图2，大致分为3个阶段[2]：辐照初期的瞬态阶段，由于〈a〉型位错环大量成核，生长应变迅速增加；随着辐照剂量的增加，〈a〉型位错环逐渐饱和，生长率下降至稳定，此时进入辐照生长第2阶段；当辐照剂量超过一定值时，〈c〉型位错环开始成核，生长率明显增加，进入“加速生长”阶段。RXA(再结晶退火)锆合金相比CW(冷加工)及SRA(消应力退火)锆合金的“加速生长”趋势更加明显。

宏观经验模型及介观力学模型都可描述包壳管蠕变和生长不同阶段的变形规律。对不同类型的包壳管材料，其蠕变和生长应变随中子注量变化的趋势是相似的(如图1～2)，因此可通过调整经验模型及力学模型的模型参数预测不同类型锆合金包壳管材料的蠕变和生长行为。

1.2 宏观经验预测模型

宏观经验模型假设辐照变形由独立的、可叠加的3部分变形构成[3]，包括热蠕变、辐照蠕变、辐照生长，总变形率为：

(1)

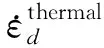
Matsuo[14]根据Zr-4包壳管在内压作用下的热蠕变特征，提出了适用于锆合金包壳管的热蠕变模型，该模型通过双曲正弦函数将稳态热蠕变率与外加应力联系起来。根据应力水平，指数n的取值范围在2～4之间[15-16]。

(2)

文献[3,14,17]在式(2)的基础上，同时考虑材料的初始热蠕变及稳态热蠕变，描述总的热蠕变应变随时间的变化：

(3)

Hoppe[18]假设辐照蠕变主要是由非热机制引起的，提出了适用于锆合金包壳管的辐照蠕变经验模型，辐照蠕变速率与外加应力和中子注量率呈幂律关系：

(4)

Luscher等[16]在Hoppe等的基础上，考虑了辐照蠕变对温度的依赖，同时修正应力项为等效应力，并根据Franklin等[19]的试验数据拟合修正了模型参数：

(5)

其中，f(T)为温度依赖系数。对于SRA及RXA锆合金包壳管，应力指数C2=1.0、快中子注量率指数C1=0.85、温度依赖系数f(T)=0.72～1.47(服役温度在300～350 ℃之间)。当等效应力形式基于屈服准则以及应变方向由屈服面法线决定时，这种修正形式类似于塑性流动的常规表达式。

Geelhood等[16,20]提出了锆合金包壳管的辐照生长模型，在辐照生长的不同阶段，辐照生长应变以与时间有关的增量形式表示：

εt+Δt=εt+Δε

(6)

Δε=AGd(φΔt)m

(7)

其中：εt为t时刻的生长应变；Δε为Δt时间内的生长应变增量；φ为快中子注量率；A、Gd及m为材料常数，A和m由合金成分和加工方式决定，Gd为生长各向异性因子，在d特征方向上，Gd=1-3fd，fd为Kearns各向异性织构因子。

1.3 介观力学预测模型

Montgomery等[3]提出了以VPSC框架为基础的介观模型思想。即通过VPSC程序耦合锆合金的单晶蠕变和生长模型，在多晶尺度上综合考虑多晶织构、晶粒间相互作用、晶粒尺寸和晶粒形状效应，模拟锆合金多晶的辐照变形行为。

1) 辐照变形物理机制与单晶模型

热蠕变机制主要有扩散控制及位错控制两种类型。扩散控制的蠕变机制假设热蠕变率与应力呈线性依赖关系[21-22]，包括Nabarro-Herring蠕变(体扩散)[23]及Coble蠕变(晶界扩散)[24]。位错攀移控制的蠕变机制假设热蠕变率与应力满足幂律关系，幂指数随应力的变化在4～9之间分布[25-27]。Montgomery等[3]采用黏塑性幂律规则描述不同滑移系对热蠕变的贡献，在锆合金构件正常服役的情况下，幂指数n取4，单晶热蠕变率为：

j=1,2,…,5

(8)

(9)

(10)

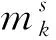
辐照蠕变机制主要有应力诱导的优先吸收(SIPA)机制[29-30]、攀移增强滑移机制[31]、应力诱导的优先成核(SIPN)机制[32]及扩散传质机制[33]，其中前两者较为突出[11]。SIPA机制假设自间隙原子优先被柏氏矢量平行于应力方向的刃位错捕获，空位优先被柏氏矢量垂直于应力方向的刃位错捕获，这种捕获偏差导致材料产生沿应力方向的伸长现象[34-35]。攀移增强的滑移机制假设刃位错捕获辐照产生的点缺陷发生攀移，克服障碍后在另一个滑移面上继续滑移[36-38]，从而进一步产生变形，最具代表性的是Gittus的I-creep模型[39-40]。目前学术界对锆合金的辐照蠕变机制仍无明确定论，包壳管的辐照蠕变计算仍以经验模型为主。Patra等[41]在经验模型基础上，假设蠕变率与应力及中子剂量率呈正比，在单晶尺度上考虑每个滑移系对变形的贡献，开发了辐照蠕变晶体学模型，单晶辐照蠕变率为：

j=1,2,…,5

(11)

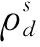
辐照生长的物理模型主要有辐照损伤理论(RDT)模型、点缺陷各向异性扩散差异(DAD)模型及反应-扩散模型。RDT模型假设辐照损伤过程产生等量的空位和自间隙原子，它们的运动都是各相同性的，微观结构演化的驱动力来自刃位错对自间隙原子的优先捕获[42-43]，这并不能解释试验观察到的辐照生长现象[44-45]。在此基础上，DAD模型考虑到自间隙原子优先沿基面a方向迁移，易被柱面位错捕获；空位迁移近似为各向同性，易被基面位错捕获，这可解释锆合金晶胞沿c轴的收缩行为，以及〈c〉位错环在锆合金“加速生长”的行为中扮演至关重要的角色[46-47]。但DAD模型没有考虑到辐照使材料内部产生大量可动缺陷团簇的情况，这与试验和分子动力学模拟结果不符[34,48-49]。Golubov等[44-45]将模拟bcc和fcc晶体辐照肿胀的生产偏差模型(PBM)思想应用于锆合金辐照生长模型中，称为反应-扩散模型。该模型考虑最初的辐照损伤由点缺陷及自间隙原子团簇组成，忽略了点缺陷迁移的各向异性，但考虑自间隙原子团簇沿基面一维迁移。Patra等[41]在Golubov等的基础上，进一步考虑了晶界捕获辐照点缺陷发生收缩或膨胀对辐照生长的贡献，具体如图3所示。

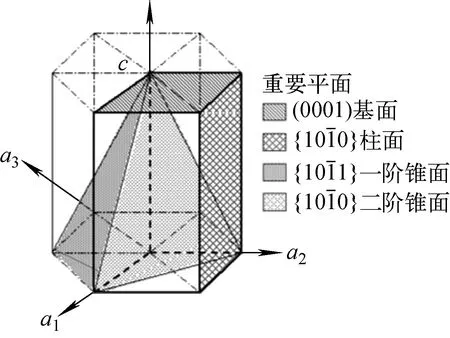
图3 锆合金HCP晶胞的晶体学特征[2] Fig.3 Crystallographic characteristics of zirconium alloy HCP elementary cell[2]

Patra等考虑辐照生长率由位错捕获点缺陷发生攀移及晶界吸收点缺陷两部分贡献。位错捕获点缺陷对辐照生长的贡献(忽略位错线与位错环捕获强度的差异)为：

(12)

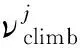
j=a1,a2,a3

(13)

(14)

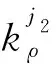
晶界吸收点缺陷发生收缩或膨胀由晶界捕获点缺陷的净通量决定，对辐照生长的贡献为：

j=a1,a2,a3,c；m=x′,y′,z′

(15)

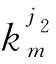
由以上公式可得总辐照生长率：

(16)

Christiaen等[50]采用蒙特卡罗方法计算分析得出，锆合金中空位运动也是各向异性的，沿平行于基面的方向扩散较快。Patra等[41]的反应-扩散模型假设空位和自间隙原子运动都是各相同性的，虽然模拟辐照生长应变随辐照剂量的变化趋势与试验结果较为接近，但其在理论上仍存在进一步发展空间。

2) VPSC框架

VPSC程序由Tomé等于1993年提出，基于单晶变形时滑移和孪生的物理剪切机制，考虑材料织构及晶粒间相互作用，模拟多晶在外部约束(应力、应变、高温、辐照等)下的各向异性的塑性变形[51]。VPSC将每个晶粒看作一个嵌入在有效黏塑性介质中的椭球形黏塑性夹杂，夹杂和介质都是各向异性的(图4)。当对有效介质施加应力、应变率或辐照时，介质与晶粒发生相互作用，在晶粒及其附近产生局部应力。当晶粒为椭球时，晶粒中的应力是均匀的，但可能与介质中应力存在偏差。VPSC的自洽性即通过循环迭代强制实现所有晶粒上的平均应力和应变率等于施加在介质上的宏观应力或应变率[51-52]。

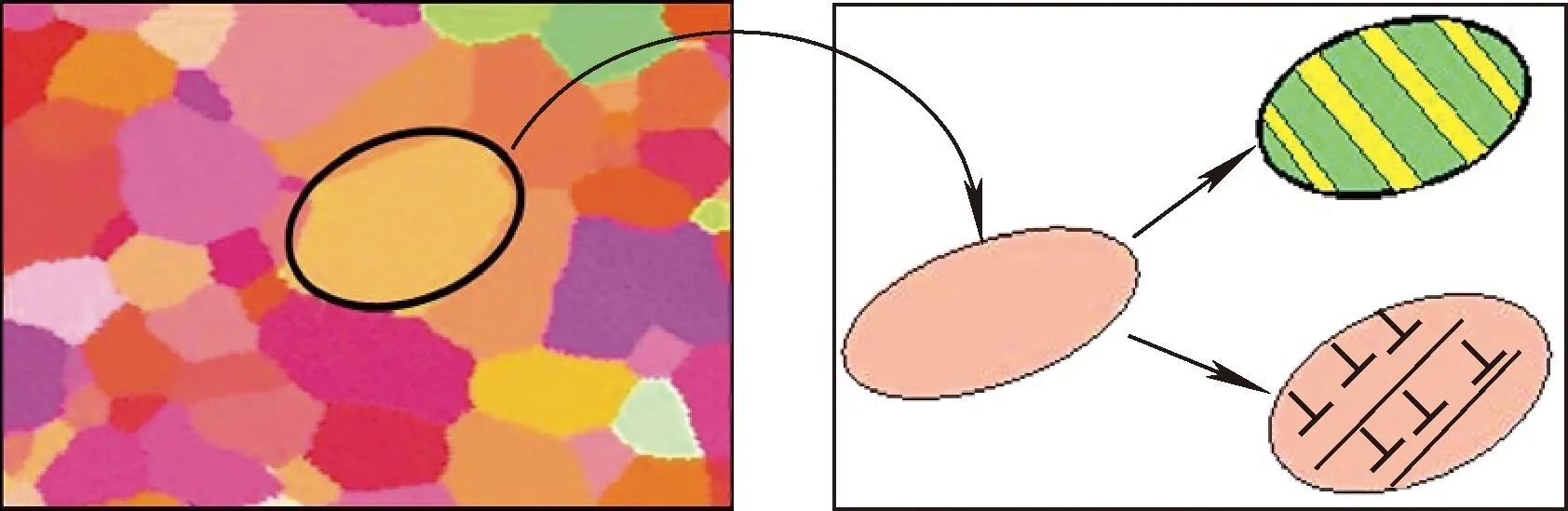
图4 VPSC机制示意图Fig.4 Schematic diagram of VPSC mechanism

式(17)基于非线性速率敏感性方程，通过对所有滑移系s上的变形速率累加，描述了VPSC中的单晶变形速率(VPSC在计算过程中应力及应变率均用5维矢量形式表示[51])，并假设变形速率与应力呈线性关系：

i=1,2，…,5

(17)

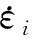
(18)

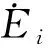
(19)

其中：I为单位矩阵；S为Eshelby张量，与晶粒形状及宏观粘塑性蠕变柔度张量有关。

(20)

(21)

3) 辐照蠕变和生长在VPSC中的实现

Patra等以VPSC框架为基础，在VPSC中实现了锆合金辐照生长的反应-扩散模型与辐照蠕变的晶体学模型的耦合[41]，并根据冷加工Zr-2合金的微观结构演化及辐照变形数据确定了模型参数，初步预测了单轴拉伸应力作用下锆合金的轴向变形行为。其预测结果较好地反映了试验规律[41,53-54]，表明该介观模型整体上是可靠的。但Patra等忽略了辐照初期热蠕变的贡献，而堆内试验结果表明，在辐照初期的瞬态阶段，热蠕变的贡献不可忽略(图1)。本文在Patra 等模型的基础上，增加了热蠕变修正项，假设单晶变形速率为：

i=1，2，…，5

(22)

(23)

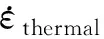
当前的介观力学模型展现了较好的预测能力，但目前辐照蠕变机制尚无明确定论，单晶蠕变模型采用了以经验模型为基础的晶体学模型，而辐照生长的反应-扩散模型中也忽略了点缺陷各向异性运动这一重要物理现象。因此，介观力学模型仍存在进一步的发展空间，其发展核心应是锆合金蠕变和生长物理机制的持续探索以及单晶模型的开发。

2 Zr-2.5Nb压力管的辐照变形预测模型

目前，Zr-2.5Nb压力管的辐照变形预测模型主要为宏观经验模型，虽然1.3节介绍的介观力学模型框架理论上也适用于压力管，但具体应用实例并未见文献报道。宏观经验模型包括C6方程及秦山方程。C6方程是Christodoulou等[55]于1996年提出的适用于CANDU重水堆压力管的模型，可综合考虑压力管的服役条件、织构、各向异性微观结构特征(位错、晶粒形状)，预测压力管各向异性的辐照变形，但相关各向异性参数并没有公开。秦山方程是唐迥然等[56]通过对秦山压力管的在役检查数据进行统计分析，在统计规律的基础上建立的一种新的压力管辐照变形计算方程，该方程符合秦山重水堆压力管变形规律，但针对不同的重水堆，方程参数需要重新拟合。

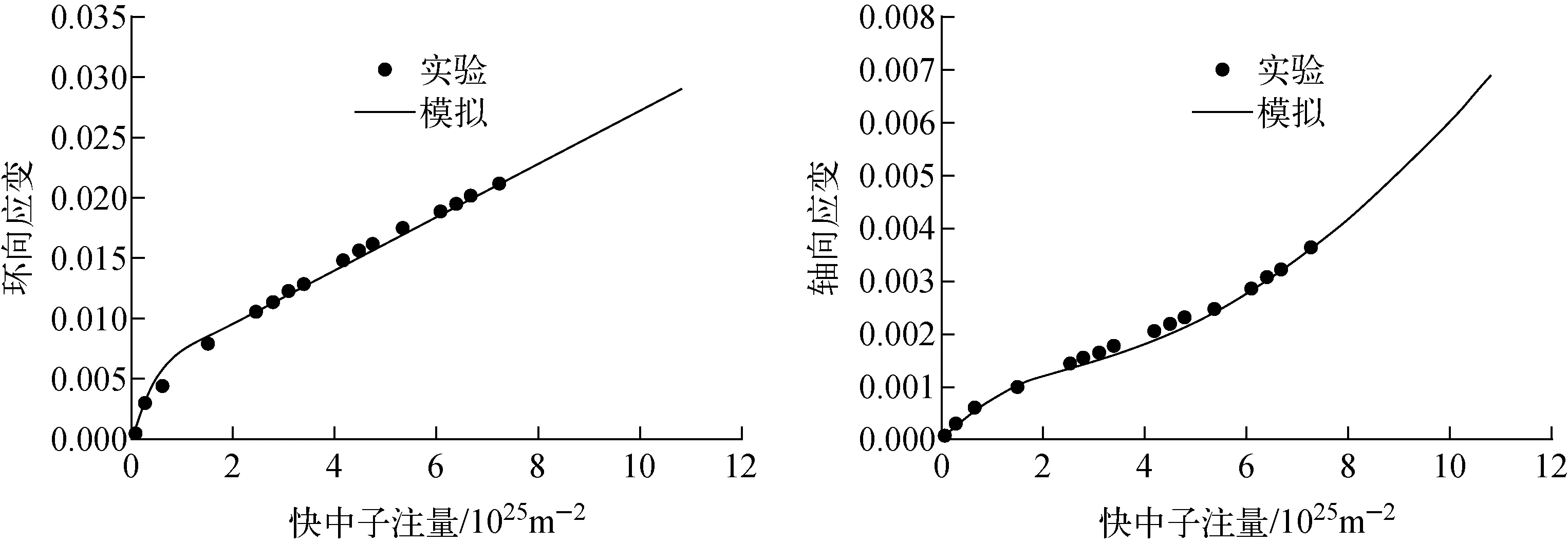
图5 SRA Zr-4包壳管辐照变形预测结果与试验对比Fig.5 Comparison between predicted result and experimental result of SRA Zr-4 alloy cladding tube

图6 RXA Zr-4包壳管辐照变形预测结果与试验对比Fig.6 Comparison between predicted result and experimental result of RXA Zr-4 cladding tube

在重水堆国产化进程中，压力管材料也需国产化，应选择一种合适的方程预测及评估国产压力管的寿命。秦山方程中的参数不能直接应用于国产化的压力管材料，当前也缺少堆内变形数据支持拟合，而C6方程中有相关文献公开的部分参数，仅涉及到微观结构及织构的各向异性参数没有明确给出(各向异性参数可基于国产化压力管的织构及微观结构计算)。鉴于C6方程有在CANDU重水堆(包括秦山重水堆)中的实际应用基础[57]，C6方程预测国产化压力管的辐照变形行为应是较为合适且可行的选择，也需相应地国产化。

2.1 压力管的辐照蠕变和生长行为的基本规律

由于压力管具有与包壳管明显不同的织构(Kearns织构因子通常为fr=0.33、ft=0.61、fa=0.06)，其蠕变和生长应变也体现出和包壳管明显不同的各向异性。OSIRIS测试堆(中子注量率为2×1018m-2·s-1)内微压力管(MPT，织构和微观结构与标准压力管类似，尺寸较小)的蠕变应变随中子注量变化的曲线示于图7a[58]，双轴应力(环向应力为160 MPa)作用下，轴向和环向的蠕变应变均为正值(包壳管的轴向蠕变应变为负值)，且都没有体现出明显的瞬态阶段，可能是因为中子注量率较高，辐照初期热蠕变即被明显抑制。微压力管的辐照生长应变随中子注量的变化曲线示于图7b[59]，与包壳管不同的是，压力管的环向生长应变不为0，轴向生长应变约为环向生长应变的2倍，同时也没有明显的“加速生长”阶段。

图7 OSIRIS堆内Zr-2.5Nb微压力管的辐照蠕变和生长曲线Fig.7 Irradiation creep and growth curve of Zr-2.5 Nb micropressure tube in OSIRIS reactor

微压力管的蠕变和生长应变随中子注量的变化规律能直接反映标准压力管蠕变和生长行为的宏观规律，但与微压力管不同，标准压力管长6 m、直径104 mm、厚度4.2 mm，沿轴向不同位置，其微观结构与织构略有不同，服役时温度、应力及中子注量分布也有一定差异[12]。这些因素导致压力管产生沿轴向的不均匀变形(图8)，进一步增加了预测模型开发的难度。

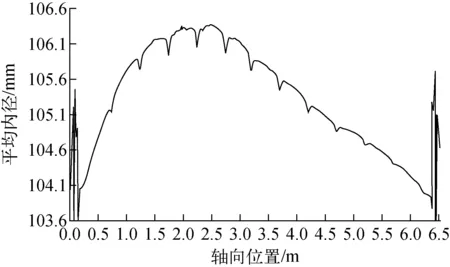
图8 典型的CANDU 压力管平均内径沿轴向的分布[12]Fig.8 Average inner diameter distribution along axis of typical CANDU pressure tube[12]

2.2 宏观经验预测模型

1) CANDU 压力管C6方程

加拿大原子能公司(AECL)对Zr-2.5Nb压力管进行了多年材料辐照试验研究(包括辐照生长、辐照蠕变和热蠕变试验)，建立了Zr-2.5Nb压力管在CANDU反应堆中的辐照变形计算方程(C6方程)，并不断进行改进，于1996年最终定型。总变形率为3种变形模式的叠加，其中热蠕变率、辐照蠕变率、辐照生长率[55]分别为：

(24)

(25)

(26)

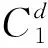
σi=[Fi(σa-σt)2+Gi(σt-σr)2+

Hi(σr-σa)2]1/2i=1,2

(27)

其中，F、G和H为Hill各向异性屈服常数。对于热蠕变，i=1或2 (应力小于120 MPa，i=1起主导作用；应力大于200 MPa，i=2起主导作用)。由于热蠕变对总变形的贡献较小，忽略Fi、Gi、Hi对位置x的依赖，而辐照蠕变考虑了压力管不同位置处织构变化对变形各向异性的影响，各向异性屈服常数随位置x的变化为：

F(x)=Fb+(Ff-Fb)x/6

(28)

G(x)=Gb+(Gf-Gb)x/6

(29)

H(x)=1.5-F(x)-G(x)

(30)

其中：Ff、Gf、Hf分别为压力管前端的辐照蠕变各向异性屈服常数；Fb、Gb、Hb分别为压力管后端的辐照蠕变各向异性屈服常数。

热蠕变及辐照蠕变的各向异性参数可表示为：

(31)

(32)

(33)

辐照生长各向异性参数为：

(34)

(35)

(36)

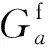
Christodoulou等[55]根据压力管堆内辐照变形数据及压力管的织构和微观结构特征拟合并计算了上述方程的参数，预测结果与堆内变形数据的对比示于图9，表明该模型能较好地预测压力管轴向及环向的变形行为。

2) 秦山压力管辐照变形计算方程

唐迥然等[56]对大量秦山CANDU重水堆压力管的在役检查数据进行统计分析，得出辐照蠕变速率及辐照生长速率分别与快中子注量率呈幂律关系，且热蠕变是不可忽略、非稳态的行为，这与C6方程明显不同。在此基础上，他们进一步建立了秦山重水堆压力管热蠕变率、辐照蠕变率及辐照生长率的计算方程，总变形率为3种变形模式的叠加：

(37)

(38)

(39)

秦山方程中沿压力管不同方向的辐照蠕变率及辐照生长率的参数需分别拟合，大量的参数拟合需要大量的堆内运行数据支持。在缺少堆内运行数据支持的情况下，C6方程预测国产化压力管的辐照变形行为应是较为合适的选择。而秦山方程描述的压力管的变形规律与C6方程明显不同，这也应作为下一步对C6方程进行改进的参考。

3) C6方程的国产化

CANDU C6方程考虑了微观结构及织构对辐照变形各向异性的影响，具备一定的物理基础，这主要体现在C6方程的各向异性参数中，而在1996年的公开文献中，这些参数并没有被公开，其计算方法也没有被详细阐述。本文将压力管热蠕变、辐照蠕变、辐照生长的单晶模型和VPSC程序耦合，输入国产化压力管的初步样品织构，计算了压力管热蠕变及辐照蠕变的各向异性屈服常数F、G、H，以及辐照生长各向异性因子，并将计算结果与Causey等计算的OSIRIS微压力管[59]进行了对比。

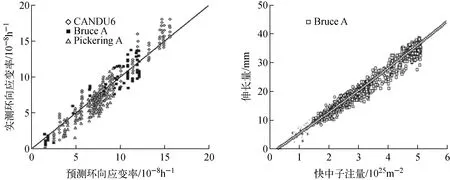
图9 Zr-2.5Nb压力管在CANDU反应堆中实测和预测结果对比[55]Fig.9 Comparison of measured and predicted results of Zr-2.5Nb pressure tube in CANDU reactor[55]

单晶热蠕变模型基于黏塑性幂律准则，幂指数n取2：

j=1,2,…,5

(40)

单晶辐照蠕变模型基于I-creep机制[61]：

k1,k2=k5,k3=k4,k6=0

(41)

其中：ki为第i类变形模式的蠕变柔度，k1为锥面滑移贡献，k2为柱面和锥面滑移贡献，k3为基面和锥面滑移贡献；σi为相应变形模式下的晶粒应力。k1、k2、k3由材料微观结构决定。

将上述单晶模型与VPSC程序耦合，采用Causey等[59]的单晶模型参数，输入国产压力管初步样品织构(织构因子fr=0.34、ft=0.57、fa=0.09)，分别计算热蠕变各向异性屈服常数Fth、Gth、Hth，辐照蠕变各向异性屈服常数F、G、H，以及辐照生长各向异性因子Ga/Gt，计算结果与Causey等[59]计算的OSIRIS微压力管(织构因子fr=0.33、ft=0.61、fa=0.06)结果的对比列于表1。

表1 国产压力管样品与OSIRIS微压力管的计算结果对比Table 1 Comparison of calculated results between localized pressure tube and OSIRIS micro-pressure tube

在织构相近的情况下，计算所得Hill各向异性屈服常数与文献结果较接近，且轴向与环向的生长率比值也较接近，可进一步基于式(28)～(36)计算各向异性参数。表明可通过该方法定量评估织构及微观结构对国产压力管辐照变形各向异性的影响。如果国产化压力管织构和微观结构与加拿大原产品接近，则这些关键的各向异性参数也应接近，且其差异可定量评估。

C6方程中压力管的辐照蠕变率及辐照生长率均与快中子注量率呈线性关系，这与秦山方程的乘幂形式明显不同，下一步可考虑参考秦山方程的形式，结合已发表的CANDU压力管蠕变和生长的堆内试验数据对C6方程进行进一步改进。但无论是C6方程还是秦山方程，都是经验性的，其经验参数值受材料类型及环境参量影响，具有一定的局限性。而理论上1.3节介绍的介观力学模型框架也适用于压力管，鉴于介观力学模型具有更广的适用性，应是更进一步的发展方向。

3 总结与展望

锆合金构件在堆内服役过程中发生的蠕变及生长行为严重影响了其使用可靠性。预测锆合金的辐照蠕变和生长对保障反应堆安全、有效运行具有重要意义。

对压水堆用锆合金包壳管，宏观经验模型及介观力学模型都可预测其蠕变和生长行为。介观力学模型基于锆合金辐照变形物理机制，理论上可预测具有任意微观结构特征的锆合金多晶在任意环境参量作用下的蠕变及生长行为，相比宏观经验模型，其理论性更强，适用范围更广，将是未来的发展趋势。当前介观模型已初步展现了较好的预测能力，但其蠕变和生长物理机制及相应的单晶模型仍存在进一步的发展空间。

对重水堆用Zr-2.5Nb压力管，主要的预测模型为宏观经验模型，包括CANDU C6方程及秦山方程。C6方程相比秦山方程具备一定的物理基础，是预测国产化压力管材料辐照变形行为较为合适的选择。当前C6方程的国产化研究已取得了阶段性进展，但用C6方程描述的压力管的蠕变和生长速率对中子注量率的依赖规律与秦山方程有明显区别，下一步应考虑参考秦山方程的形式，结合压力管蠕变和生长的堆内试验数据对C6方程进行进一步修正。同时，考虑到C6方程和秦山方程均为经验模型，其适用范围受限，因此，结合介观力学方法发展机理性的辐照蠕变和生长模型应是未来的一个重要发展方向。