双参数冻融模型在北方旱区干旱期土壤水预测中的应用

2021-01-21崔进

水利技术监督 2021年1期

崔进

(辽宁省铁岭市银州区水利局，辽宁铁岭 112000)

土壤水的预测，对于区域抗旱决策和农业用水规划十分重要[1]。北方由于气候特征，在夏、秋季易出现较为明显的旱情，通过对土壤水变化趋势的分析，可以为制定旱情应对措施提供重要的依据[2]。当前，对于土壤水的预测，主要为两种方法，第一种方式主要采用水文模型的方法[3- 6]，以土壤水作为中间变量，对其进行模拟计算，这种方式的优点在于不需要土壤水长系列的观测数据，可通过水文模型参数移植，进行土壤水的预测分析。可重点解决无土壤水观测数据的预测分析，但这种方式的缺点在于需要掌握水文模型的计算原理，通过设置中间变量，实现土壤水预测值的输出，操作难度较大。第二种方式为采用回归方程的方法[9- 13]，基于区域长系列的土壤含水量实测数据，建立回归方程或基于数学模型对未来土壤水的变化趋势进行预测，这种方式的优点在于可符合区域土壤水变化的实际情况，检验后的回归方程和数学模型模拟的土壤水精度一般较高，但缺点在于需要长系列的观测数据作为支撑，使得建立的回归方程或者数学模型具有较好的计算精度。北方属于我国的粮食主产区，为保障旱期农业用水，需要对其土壤水进行预测，从而保障农业生产。近些年来，北方地区干旱发生的频次较高，土壤水监测站点较多，分布也较为广泛，因此本文采用当前应用效果较好的双参数冻融模型[14]，以辽宁西部作为典型区域，结合区域土壤质地和土壤水数据，对旱情土壤水进行预测，并结合实测土壤水数据对模型的预测精度进行验证。成果为北方旱区土壤水预测方法提供重要的参考。

1 材料与方法

1.1 试验条件

本文以辽宁西部为研究区域，辽西属于典型的大陆季风气候，夏季干燥少雨，极易出现干旱，素有“十年九旱”的称号，为此本文选取辽西为典型区域，区域土壤类型主要为棕壤和褐土，对各土壤水观测点的土壤质地进行采样，采用室内分析的方式对不同土壤类型的质地进行分析，分析结果见表1—2。

1.2 模型土壤水预测原理

双参数冻融模型结合土壤水监测数据，建立非线性回归方程：

H=Kta

(1)

式中，H—稳定期土壤下渗水量的累积值,mm，本文结合辽西地区的土壤水下渗特点，将稳定下渗时段设定为45min；K—稳定下渗率,mm/min;a—土壤水下渗曲线的变化指数。

2 冻融入渗模型设置

2.1 参数获取

模型需要输入的两个参数为K和a，通过试验方法建立土壤物理特性参数与下渗参数之间的非线性函数来获取以上两个参数，测定了区域两种主要土壤类型下不同耕作措施下的土壤物理特性参数，参数测定结果见表3—4。

表1 1#监测站点的土壤质地分析结果

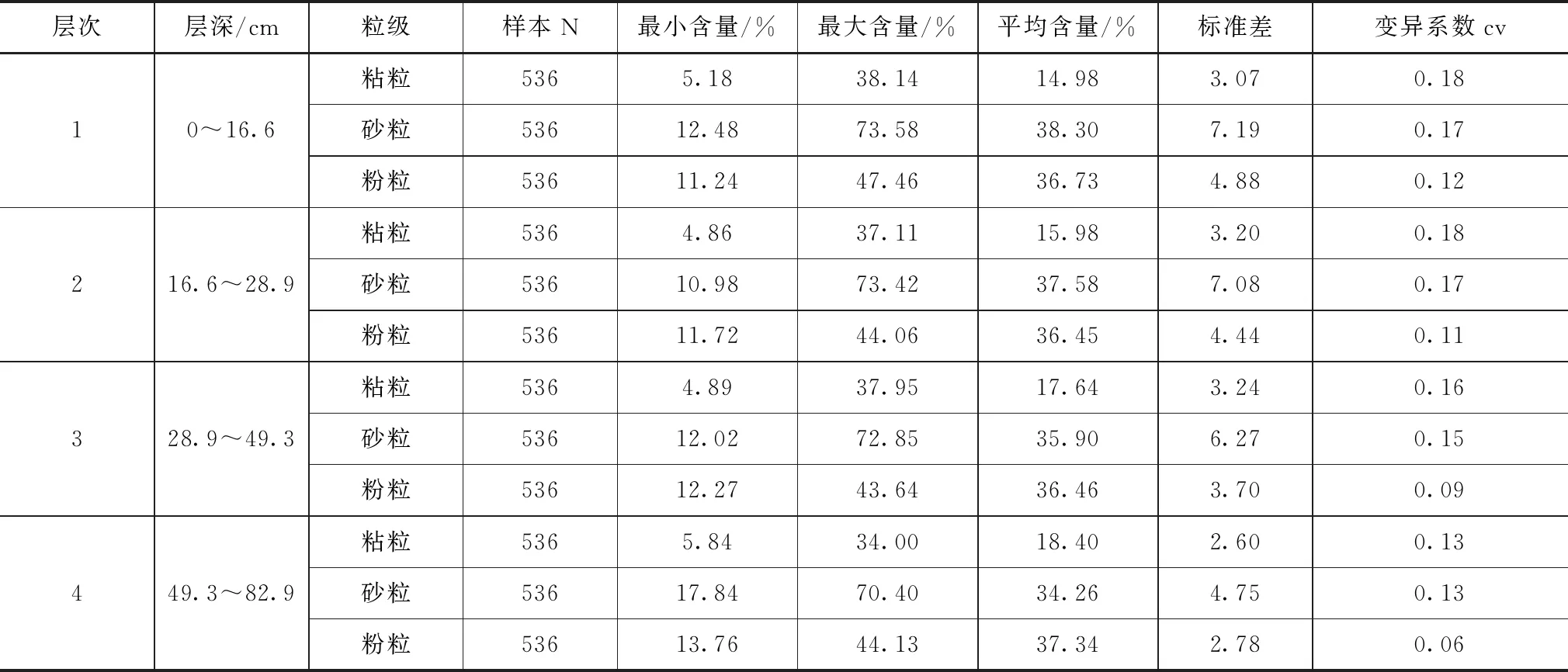
表2 2#监测站点的土壤质地分析结果

2.2 模型非线性回归方程的建立

结合区域实测土壤水数据，对不同耕作方式下的土壤物入渗物理参数的非线性变化特征进行了分析，建立了各组测定数据下的回归方程，两个观测井回归方程的分析结果见表5—6。

从表5第一个观测井土壤水入渗参数的检验结果可看出，其统计量检验值均可通过95%的回归方程显著性检验，可基于土壤入渗率参数进行回归方程的建立，犁底层由于表层土壤较少，因此不对其入渗参数K进行分析。从入渗参数a的检验结果可看出，在耕作层也可通过回归检验，基于测定的土壤水下渗数据建立的回归方程可满足检验要求。在第二个观测井不同土层土壤水入渗参数K的统计检验值要好于第一个观测井，这主要是因为第二个观测井的数据系列长度要高于第一个观测井，因此其回归方程的参数的回归检验效果较好。

2.3 模型方程非线性检验

在回归方程建立的基础上，对两个观测井土壤水预测的回归方程进行非线性特征的检验，分析结果见表7—8。

从分析结果可看出，两个土壤水入渗参数的95%F和T检验水平下的误差均低于均低于15%，两个观测井的F检验误差在8.523%～11.345%之间，构建的回归方程具有较为明显的非线性变化特征，均可通过F检验和T检验，从分析结果还可看出，各参数下的回归方程的F检验。本文建立的回归方程可用于区域土壤水监测。

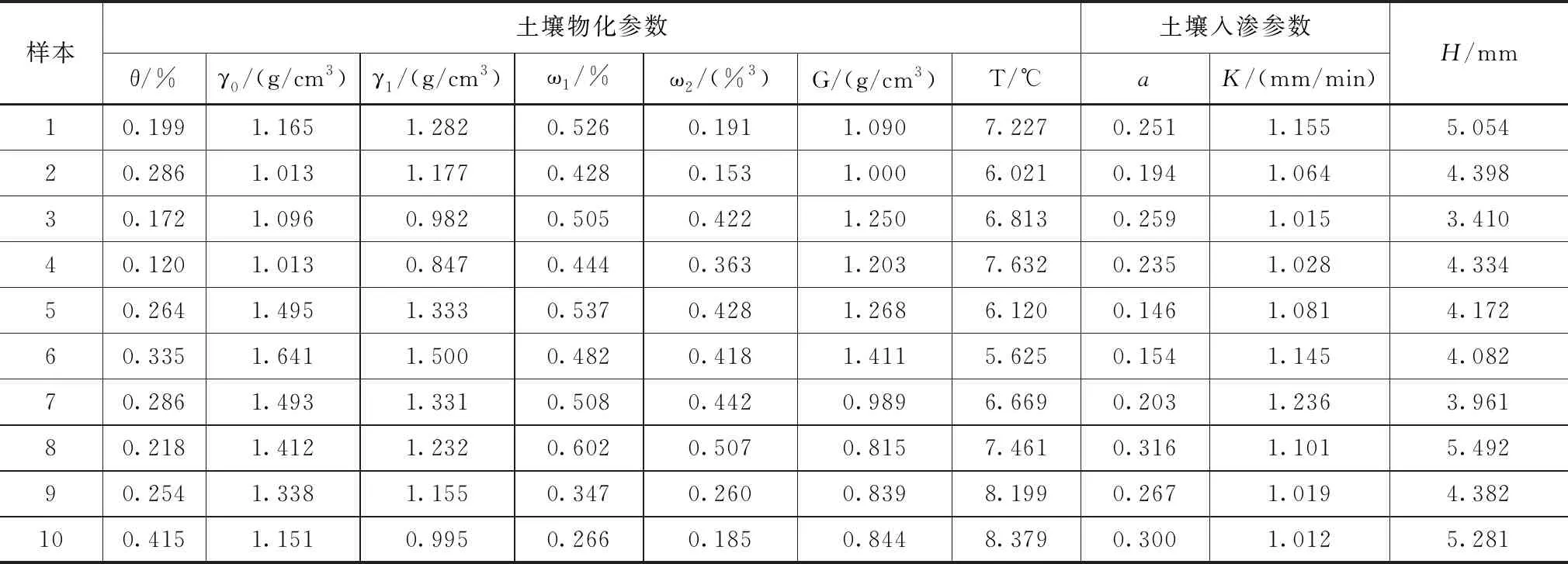
表3 1#监测站点土壤水下渗率测定结果

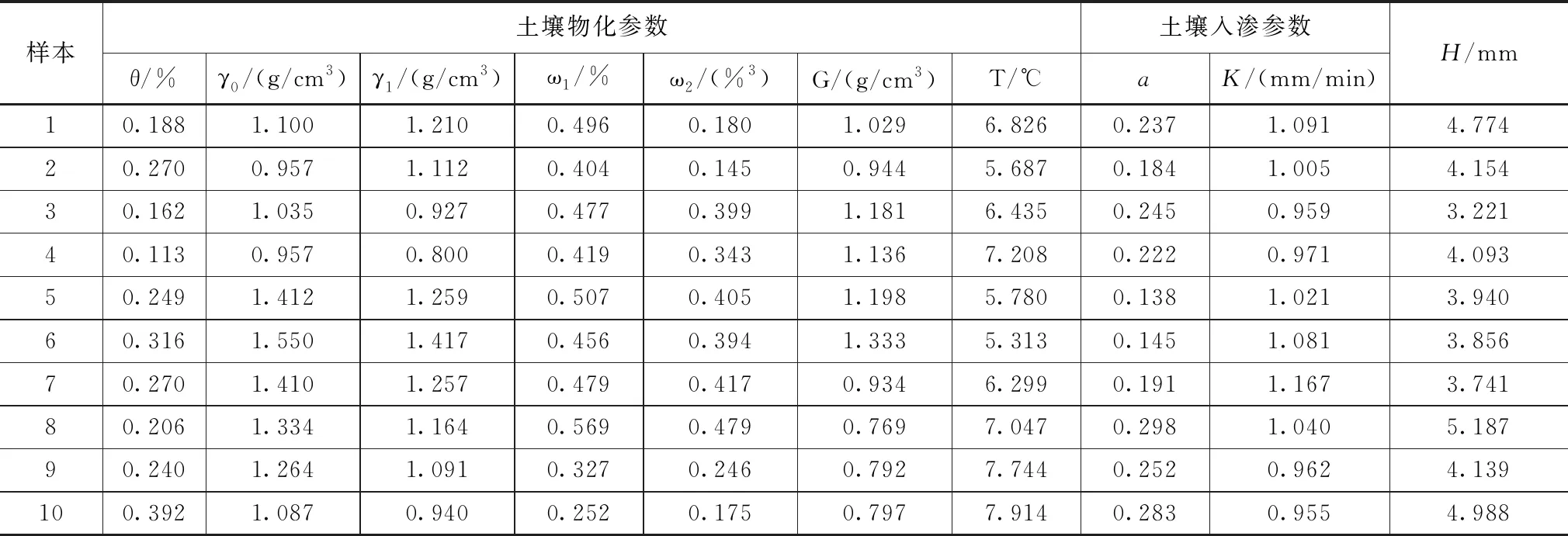
表4 2#监测站点土壤水下渗率测定结果

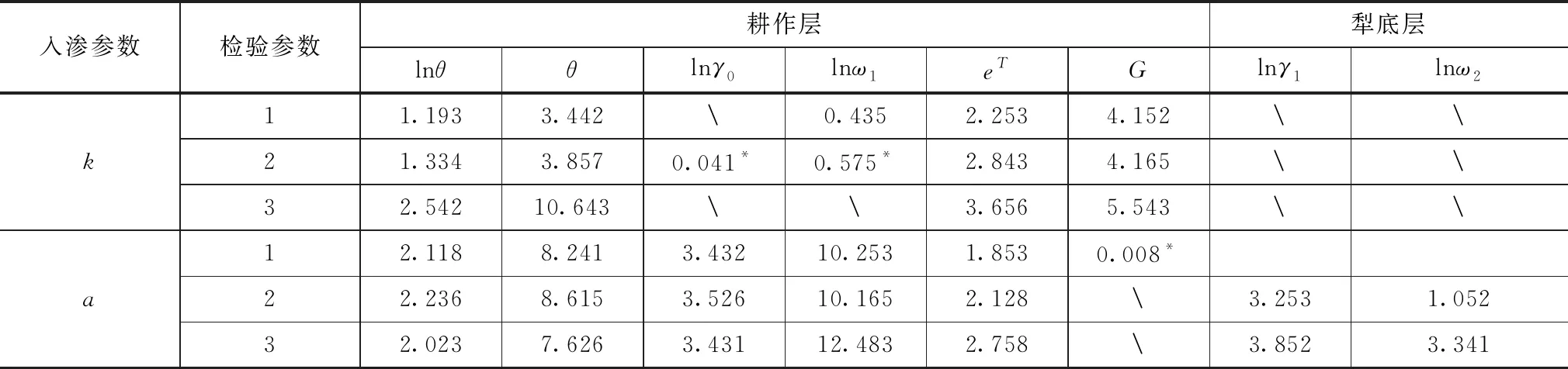
表5 1#监测站点非线性回归方程的自变量分析结果

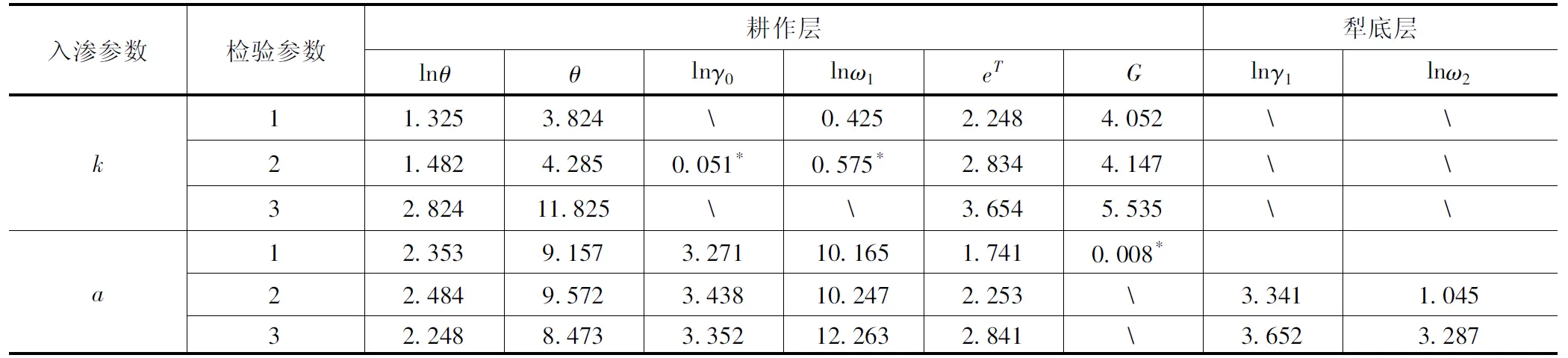
表6 2#监测站点非线性回归方程的自变量分析结果

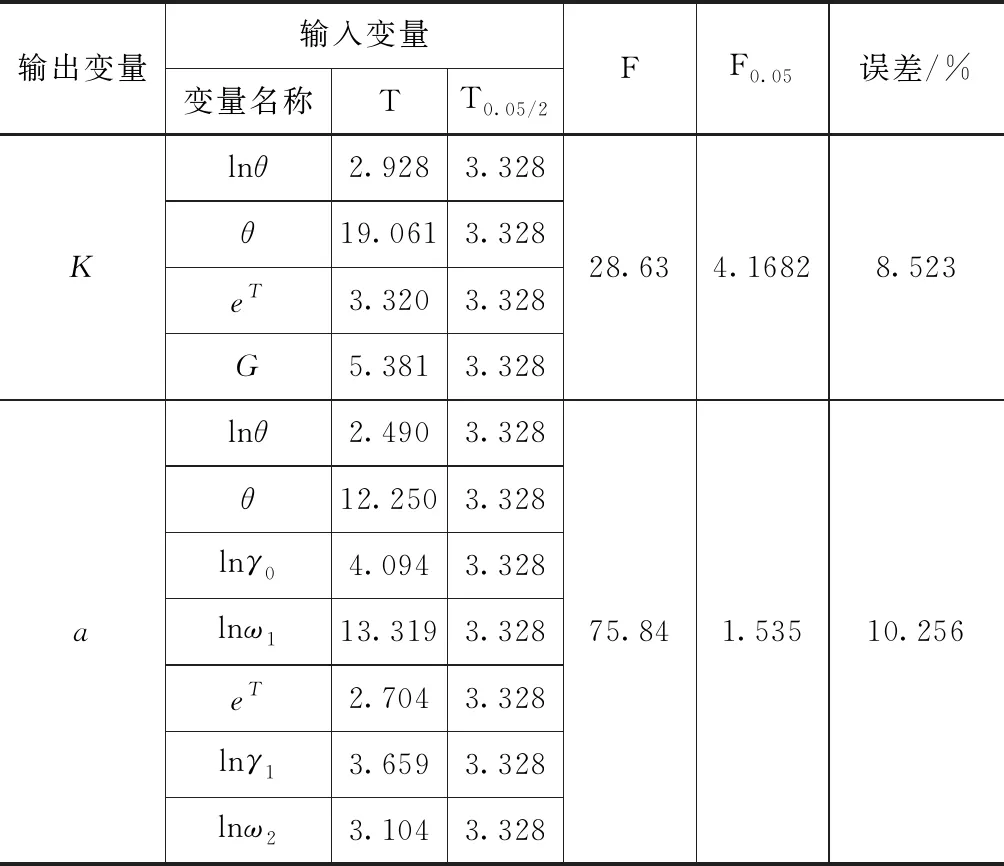
表7 1#监测站点土壤入渗非线性检验结果

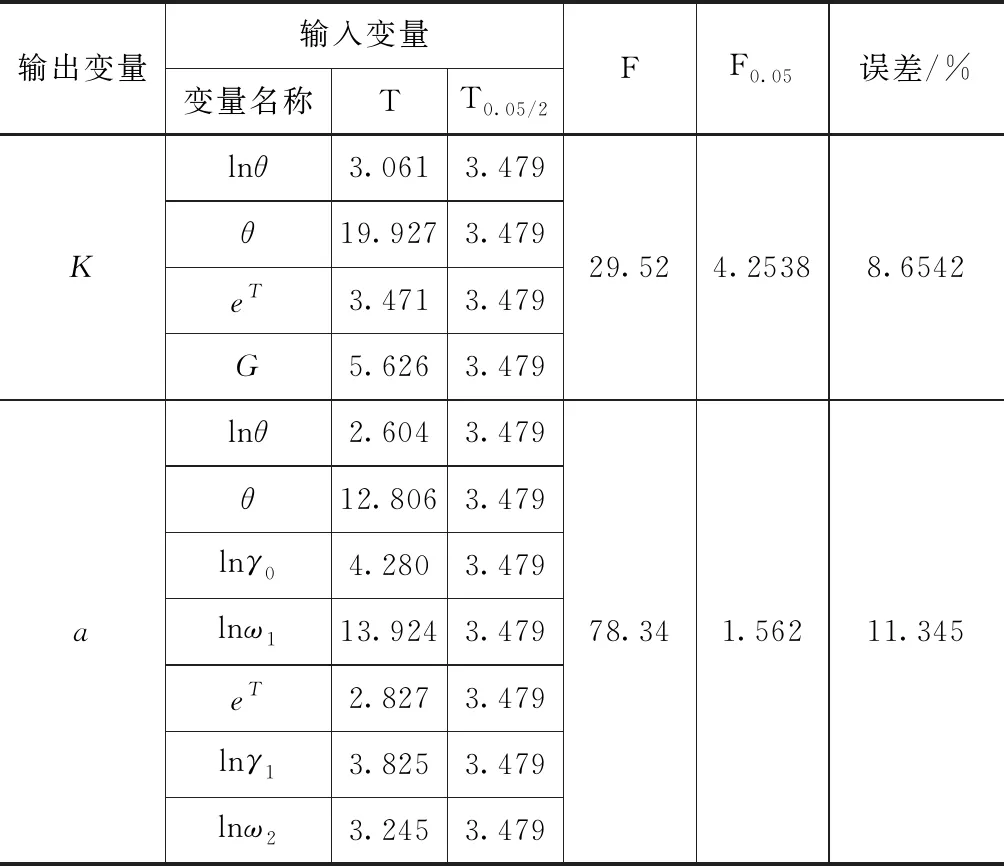
表8 2#监测站点土壤入渗非线性检验结果

2.4 预报实例分析

基于建立的回归方程，结合实测土壤水测定数据，对建立的模型进行预报检验，结果见表9—10。

从两个观测井土壤水预测值和实测的误差分析结果可看出，由于双参数冻融模型综合考虑土壤水的入渗特性，相比于传统只考虑下渗率参数的回归模型，精度有所提升，从模型误差分布可看出，两个观测井不同土壤水测定样本下的误差均在15%以内，满足土壤水预测的精度要求。可见建立土壤水入渗参数和土壤特性参数的土壤水预测非线性回归方程是解决北方旱区土壤水预测的有效措施。综上，双参数冻融模型在北方旱区土壤水预测具有较好的适用性。