优化的城市水文模型及最优LID措施模拟

李春宇

(重庆市水利电力建筑勘测设计研究院，重庆 400020)

随着城市化的快速发展及经济水平的快速提高，城镇人口日益增长，区域下垫面变化迅速，导致城镇水矛盾日益严峻[1- 2]。高密度建筑及硬化铺装工程的建设破坏了区域原有的生态平衡，当城市遭遇特大暴雨时，降雨径流形成速度过快，增加了管网排水压力甚至超出了管网排水能力，极易造成城市内涝[3- 5]，严重限制了市内交通运行，甚至威胁居民人身安全。

海绵城市的建设可使城市类似于海绵的性质，以“渗、滞、蓄、净、用、排”为关键技术，提高城市蓄水能力，降低发生内涝灾害的概率[6- 7]。低影响开发LID可基于分散式的原理对雨水径流进行限制，可缓解城市管网排水压力，改善区域生态环境[8]。不同区域可适用的LID措施有所不同，基于暴雨管理模型SWMM对城市内涝进行模拟，找寻最优LID措施是区域海绵城市构建的关键[9]。朱寒松等[10]基于SWMM模型模拟了不同LID措施的效果，比较了单一LID措施和组合LID措施的效果，指出组合LID措施效果更佳；万程辉等[11]基于SWMM模型对LID措施效果进行了评价，同样说明LID组合措施效果最好。

由于SWMM模型参数较多，率定过程较复杂，传统的SWMM模型在参数率定时，常采用人工试错法进行，该方法计算过程较复杂，且精度较差[12]。遗传算法是一种自动寻优算法，可自动找寻模型最优解，在参数率定中应用广泛[13]。本文基于遗传算法优化的SWMM模型，构建城市内涝水文模型，同时基于该模型模拟不同LID措施效果，得出最优措施。

1 研究方法

1.1 SWMM模型构建

本文选择的研究区域基本情况如图1所示。其中，研究区域面积为500hm2，平面不透水面积为50.5%，将整个区域分成109个汇水区域，管段142条，节点143个。本文SWMM模型所选择的降雨设计重现期为2a和5a，降雨历时为2h，产流模型采用Horton入渗模型，水力演算模拟动力波模型。

1.2 遗传算法优化SWMM模型参数率定

将遗传算法原理用于优化SWMM模型，可帮助模型尽快找出最优参数取值，具体步骤如下：确定SWMM计算结构，基于原始数据个数确定模型计算长度；基于遗传算法计算每个数据个体的适应度值，找出最优解；最终确定模型取值，具体原理如图2所示。

1.3 模型精度验证指标

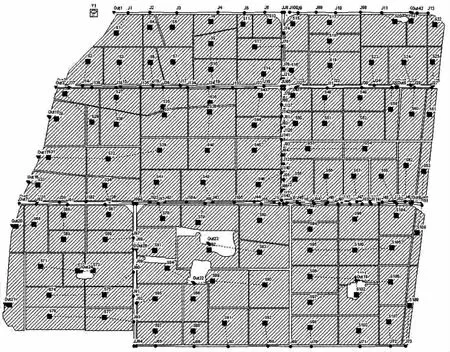
图1 研究区域概况图

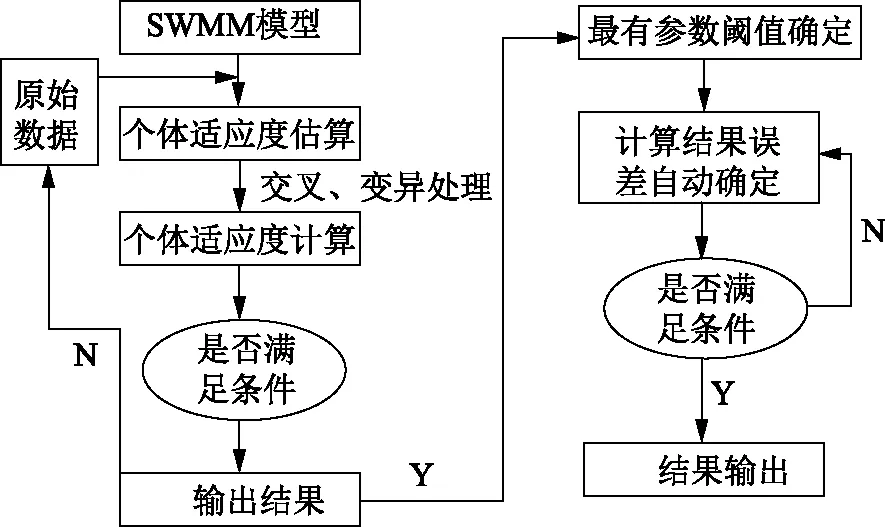
图2 遗传算法优化SWMM模型计算原理图

本文采用洪峰流量均方根误差(RMSE)，洪峰流量相对均方根误差(RRMSE)，确定系数(R2)，纳什系数(NS)和模型效率系数(Ens)[14- 15]来检验模拟值与实测值的吻合程度，具体公式如下：

(1)

(2)

(3)

(4)

(5)

2 结果与分析

2.1 模型参数率定及模型验证

基于自适应遗传算法对SWMM模型参数进行率定，率定结果见表1。由表1中可以看出，遗传算法优化后的SWMM模型和传统的SWMM模型相比，率定出同样的参数所需的运行时间不同。其中优化后的SWMM模型运行效率更高，运行时间更短。基于优化后的SWMM模型可更好地模拟城市水文。

优化后的SWMM模型在模拟期和验证期与实测值的拟合效果如图3所示。由图3中可以看出，在模型模拟期，模型为找出实测值的内在规律，与实测值的拟合效果存在一定误差。当进入验证期时，模型已自动找寻出实测值内在规律，其模拟值的变化趋势与实测值的拟合效果基本一致。

为进一步验证优化模型的精度，本文计算了在模型模拟期和验证期模型模拟结果的精度指标，结果见表2。由表2可以看出，不同时期优化模型的精度均较高，而验证期模型精度更高，2个时期的RMSE分别仅为4.53和3.17m3/s，而RRMSE仅为4.02%和3.38%，而一致性指标中，R2分别达到了0.923和0.954，NS分别达到了0.941和0.961，Ens分别达到了0.935和0.959，同时一致性指标均通过了P<0.01的极显著水平。综上所述，基于遗传算法优化的SWMM模型可作为城市内涝水文模型使用。

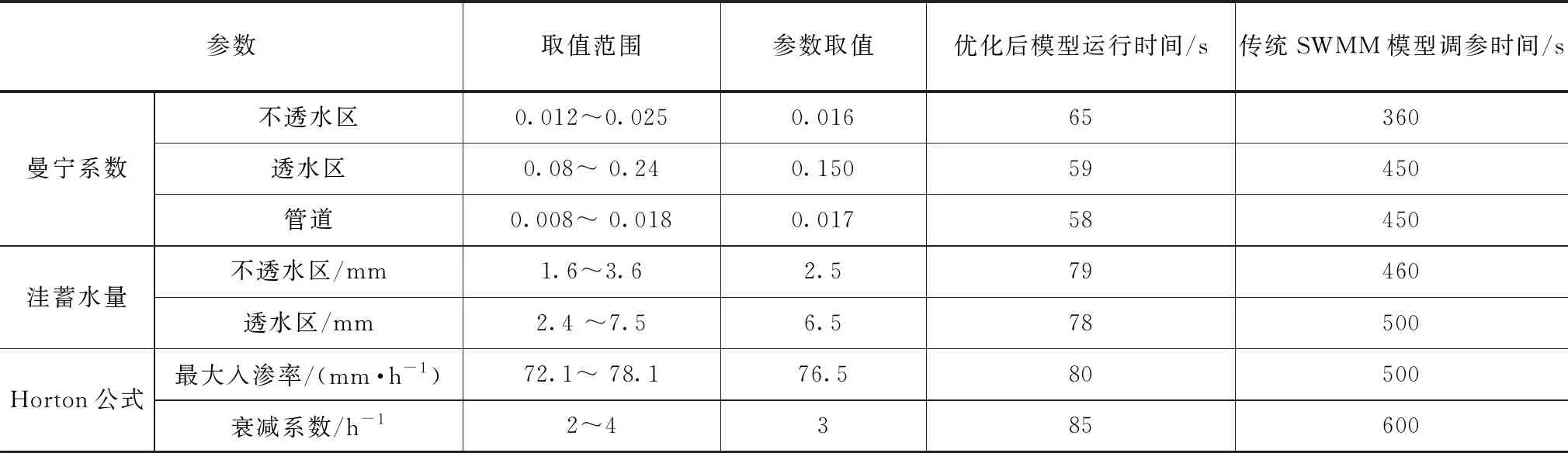
表1 遗传算法优化SWMM模型参数率定表

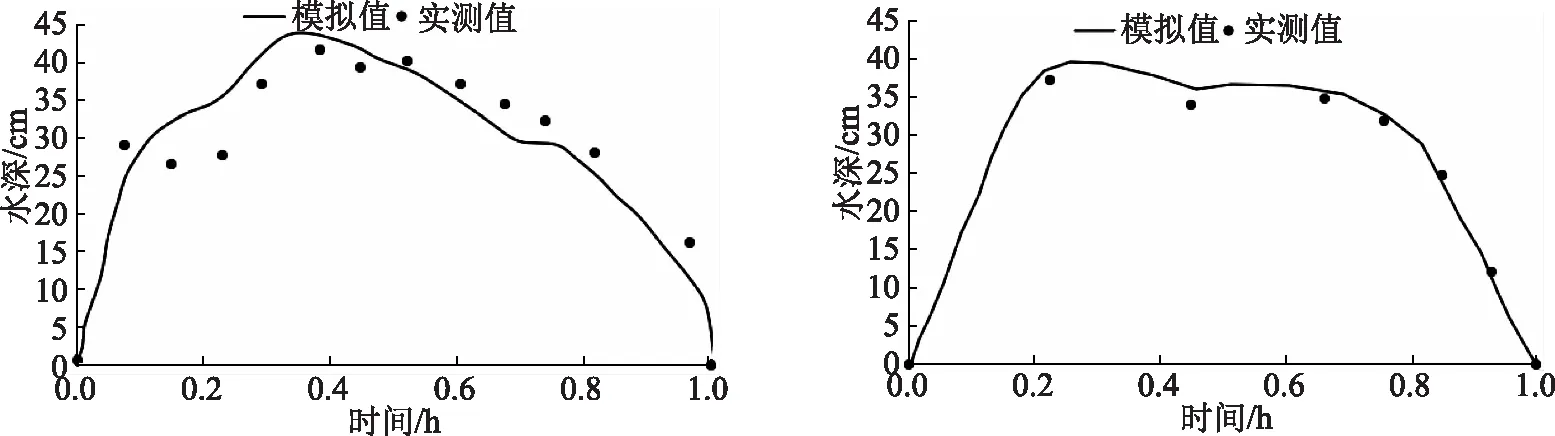
图3 模型模拟期和验证期精度拟合情况(左图为模拟期，右图为验证期)

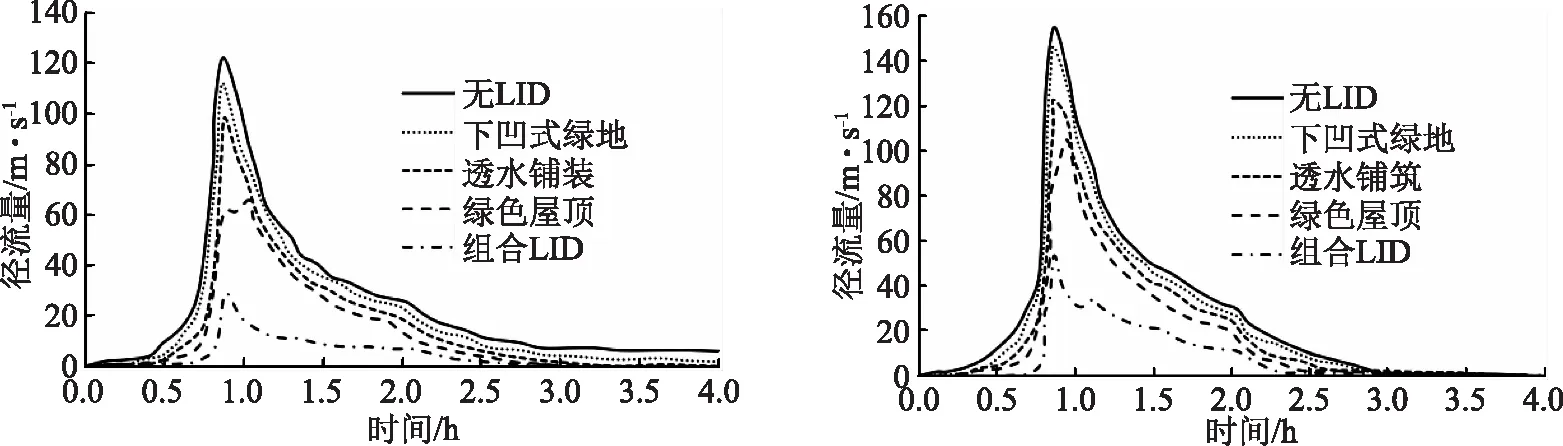
图4 不同LID措施径流削减效果对比(左图为2a一遇，右图为5a一遇)

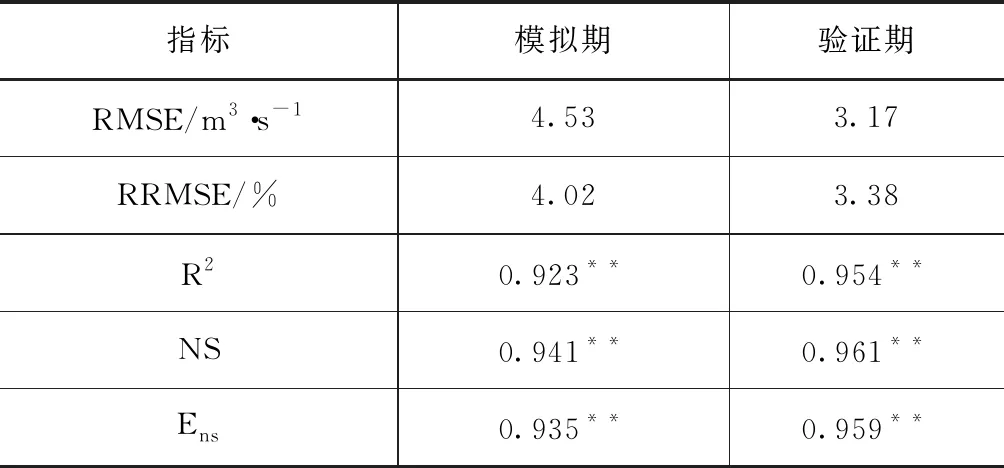
表2 遗传算法优化SWMM模型不同时期精度对比

2.2 不同LID措施径流削减效果模拟

基于遗传算法优化的SWMM模型对不同LID措施的径流削减效果进行模拟，结果如图4所示、见表3。图4反映了不同LID措施对径流削减效果随时间的变化趋势。由图4可以看出，不同LID措施对径流的削减效果不同，在不同重现期的情况下，组合LID措施的径流削减效果最佳，其次为绿色屋顶，无LID措施的径流削减效果最低。表3为不同重现期下不同LID措施对径流消减率的影响。由表3可以看出，对于径流量削减率来说，组合LID措施的效果最佳，不同重现期下的削减率分别达到了55.10%和65.46%，而对于洪峰流量削减率来说，同样组合LID措施的效果最佳，不同重现期下的削减率分别达到了44.89%和59.86%。

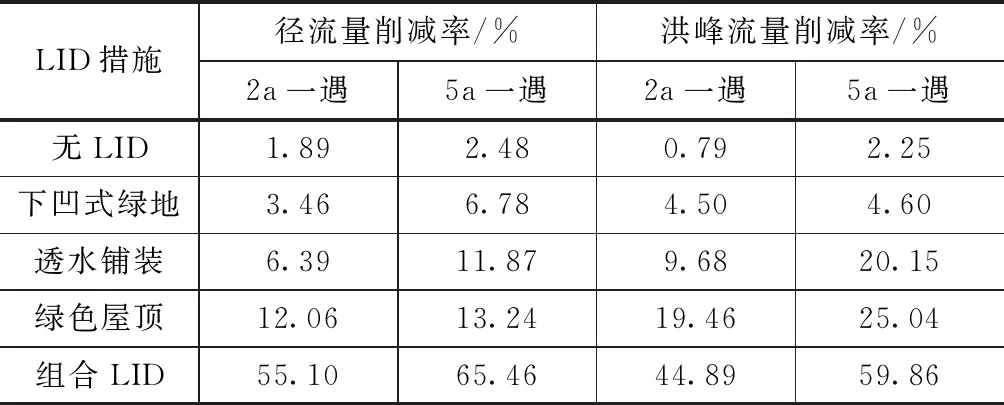
表3 不同LID措施径流削减率对比

2.3 不同LID措施水质污染削减效果模拟

为进一步比较不同LID措施的削减效果，本文基于遗传算法优化的SWMM模型模拟了不同LID措施对排水水质污染削减率的影响。选择总氮TN、总磷TP和化学需氧量COD共3项水质指标，不同重现期下3项指标的削减率见表4。由表4可以看出，组合LID措施的水质污染削减率最高，其次为绿色屋顶、透水铺装、下凹式绿地，无LID措施水质污染削减效果最低。综上所述，在进行LID设施布置规划中，建议采用多种LID措施组合布设，以取得最佳效果。

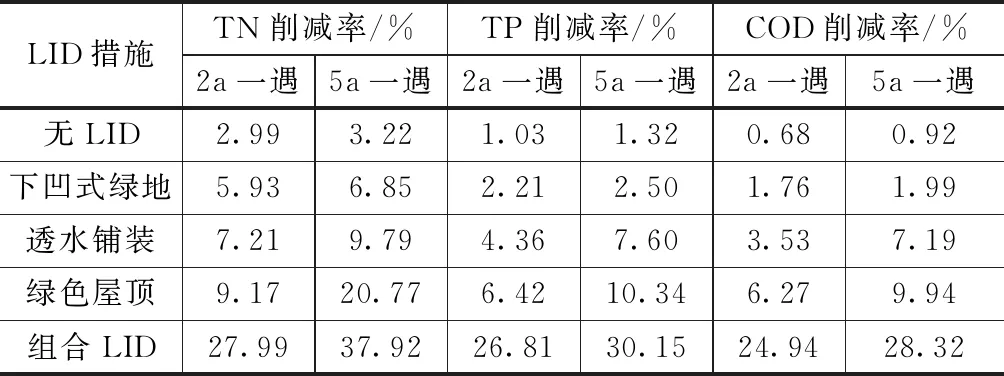
表4 不同LID措施水质污染削减率对比

3 结论

本文基于遗传算法优化的SWMM模型构建了城市内涝水文模型，并对不同LID措施径流削减和水质污染削减效果进行了模拟，得出了以下结论：

(1)基于遗传算法优化的SWMM模型相较于传统SWMM模型运行效率更高，且模拟结果在模拟期和验证期的精度较高，可作为城市内涝水文模型使用。

(2)基于优化的SWMM模型对不同LID措施径流削减效果进行了模拟，指出组合LID措施下的径流削减效果最好。

(3)基于优化的SWMM模型对不同LID措施的水质污染削减效果进行了模拟，以TN、TP和COD为例，指出组合LID措施下水质污染削减效果最佳。

(4)本文综合比较了5种LID措施的效果，指出组合LID措施效果最佳，在今后的研究中，可具体比较不同措施不同组合方式下的最优组合方式，为海绵城市的构建提供依据。