道路拓宽改造对邻近建筑地基变形影响分析与控制

王燕,谢秀栋,张飞

(1.福建江夏学院 工程学院,福建 福州 350108；2.福州大学 土木工程学院,福建 福州 350108)

0 引 言

随着城市建设的发展，道路拓宽改造项目越来越多。在软土地基上填筑路基不仅施工困难，而且拓宽道路本身及施工过程产生的荷载还会造成道路周边已有建筑产生不均匀沉降、倾斜甚至开裂，严重影响既有建筑的安全和正常使用[1-6]。因此，找出一种有效的沉降计算方法，研究邻近建(构)筑物地基的沉降变形规律，对于道路施工运营和保证邻近建(构)筑物安全使用具有重要意义。陈民勇等[7]采用数值分析方法研究了拓宽路基修筑完成后变形特性及应力、孔压变化规律；贾宁等[8]通过分析杭甬高速公路拓宽工程的监测数据，研究了老路堤和拓宽路堤的沉降变形规律。陈磊等[9]对新、老路基采用不同处理方法的效果进行了数值模拟,认为新路基采用复合地基法处理能较好地解决不均匀沉降问题。现有关于拓宽道路的研究主要是对路基本身的沉降和稳定性进行工程实测、现场试验和理论计算，而对周边已有建筑沉降变形研究较少。此外，关于地基沉降的研究大都以固结理论为依据采用分层总和法进行[10-12]，虽然计算结果会根据施工方案和土质特性进行修正，但是由于忽略软土的流变性，造成计算结果与实际不符。

基于现有研究不足之处，本文结合福建地区某道路拓宽改建项目，拟合现场实测沉降数据，总结了拓宽道路施工期和运营期邻近出水池地基的沉降变形规律。利用ABAQUS有限元软件，考虑软土的蠕变-固结耦合效应，建立包含施工道路及邻近出水池地基在内的整体模型，充分考虑拓宽道路与出水池地基变形的相互关系，提出一种附加荷载作用下软土地基变形的有限元分析预测方法，并与太沙基一维固结理论沉降计算结果和实测数据进行对比分析，验证了该方法的可行性和合理性。

1 工程背景

福建省某排涝工程由进水池、主泵房、出水池、副厂房等组成，排涝面积11.71 km2。邻近排涝站的某道路拓宽改建项目道路全长4.16 km，规划红线宽40～80 m，道路等级为城市I级主干道，具体位置平面布置见图1，其中1～3为监测点。从道路施工开始，大部分重载车辆都靠出水池旁新建成的人行道单车道行驶。同时，在道路路基填筑施工过程中，出水池侧墙背侧也出现较大的临时堆载和施工荷载，导致原先预留的沉降缝出现较大的不均匀沉降，这些都严重影响出水池的正常运行。

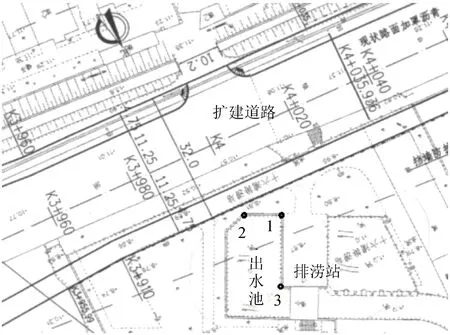
图1 排涝工程平面布置图

2 现场沉降监测

2.1 荷载工况

假设排涝站施工前地基土体处于正常固结状态，则从排涝站建成到道路投入运营，不同工况下施加的荷载如表1～2所示，荷载的取值按国家现行有关标准确定。

表1 各工况分级加载情况

表2 各项荷载取值

2.2 实测沉降变形规律

沉降测管布设在测点1和测点2位置处，测点2为出水池结构地基表面最靠近拓宽道路的一点，理论上该点为地基沉降最大点，因此将该点作为地基沉降控制点。为进一步分析水池地基发生沉降变形的主要土层及其分层沉降变形规律，除了对测点2原地基表面的沉降变形进行监测外，同时在出水池地基不同深度处埋设分层沉降磁环，监测各土层分层沉降情况。沉降数据监测时间从拓宽道路开始施工到投入运营1 a。

图2为出水池地基表面测点1和测点2的现场实测沉降数据拟合曲线，可以看出，随着路基填土荷载和施工荷载增加，测点2的沉降量大于测点1的沉降量。道路施工结束时测点2沉降量为87 mm，测点1沉降量为38.2 mm，两者的沉降量差值为48.8 mm。道路运营1 a后测点2沉降量为104.5 mm，测点1沉降量为50.7 mm，两者的沉降量差值增大至53.8 mm。由此可见，距离拓宽道路越近，出水池地基沉降量越大，出水池地基在邻近道路一侧和远离道路一侧产生差异沉降，由于出水池基础底板刚度远大于地基刚度，差异沉降使基础底板出现次内力，并最终导致出水池结构产生裂缝，影响正常运行。

图2 测点1，2实测地表总沉降量曲线

图3为测点2实测分层沉降量随时间的变化曲线。由图3可知，不同深度处，各土层的沉降变形规律基本相同。道路施工期间，随着填土荷载增大，各土层沉降速率迅速增大，沉降量增加。道路运营阶段，同一深度处出水池地基土压缩量随时间逐渐增大，但沉降速率逐渐降低，沉降曲线趋于平缓。此外，同一时间段上，浅部土层沉降速率大于深部土层的沉降速率。

道路投入运营1 a后,4.21 m厚回填砂土层压缩量为27.7 mm，3.79 m厚浅部淤泥质土层压缩量为36.8 mm，4 m厚中部淤泥质土层压缩量为26 mm，下部土层压缩量为14 mm，即分层沉降量最大的土层发生在压缩模量小的软土层中。道路施工结束时回填砂土层压缩量为25.8 mm，已经达到运营1 a后总压缩量的93%，这是由于回填砂渗透系数大，固结作用较强的缘故。

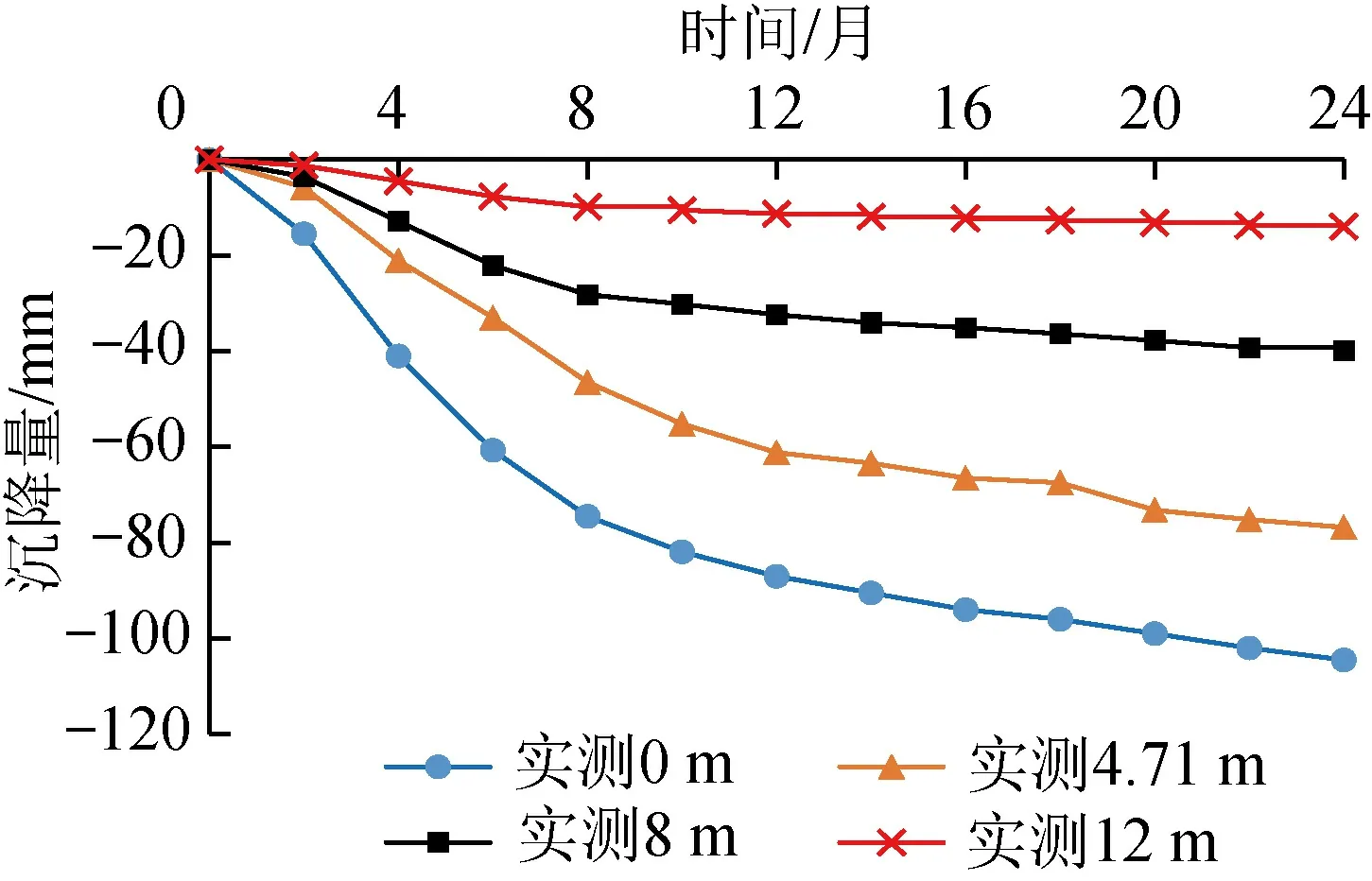
图3 测点2实测分层沉降量曲线

3 有限元分析

3.1 计算模型

根据工程实际，地基土体水平方向取40 m，竖向深度取计算压缩层厚度16 m，其中回填砂厚4.21 m，淤泥厚11.79 m，整个边界尺寸基本能消除边界效应对计算结果的影响。

位移边界条件为：左、右边界X方向位移为0；前后边界Y方向位移为0；底边完全约束，X，Y，Z方向位移为0；上表面边界自由。

排水边界条件为：左、右边界，前、后边界均为不透水边界；底面边界亦为不透水边界。地基上表面为排水边界，边界水压为0。整个模型网格划分如图4所示。

图4 模型有限元网格划分

3.2 本构模型

研究表明，软土的蠕变特性和固结特性既相互作用又相互影响，软土地基的变形是蠕变效应和固结效应共同作用的结果，其耦合效应决定软土地基的变形和稳定[13-14]。基于此，该项目软土本构模型选用扩展的D-P屈服准则耦合时间硬化率蠕变模型，该模型考虑偏应力不变量J3的影响，嵌入了蠕变法则和固结理论，能够较好反映土体材料的非线性特性[15-16]。

3.3 模型参数选取

计算参数根据岩土工程勘察报告和排涝站初步设计报告，并参考该地区地基土层物理力学性质指标统计表。其中，蠕变模型参数在文献[17]试验数据基础上，利用等效蠕变应变率公式进行拟合得到。具体物理力学指标如表3所示。

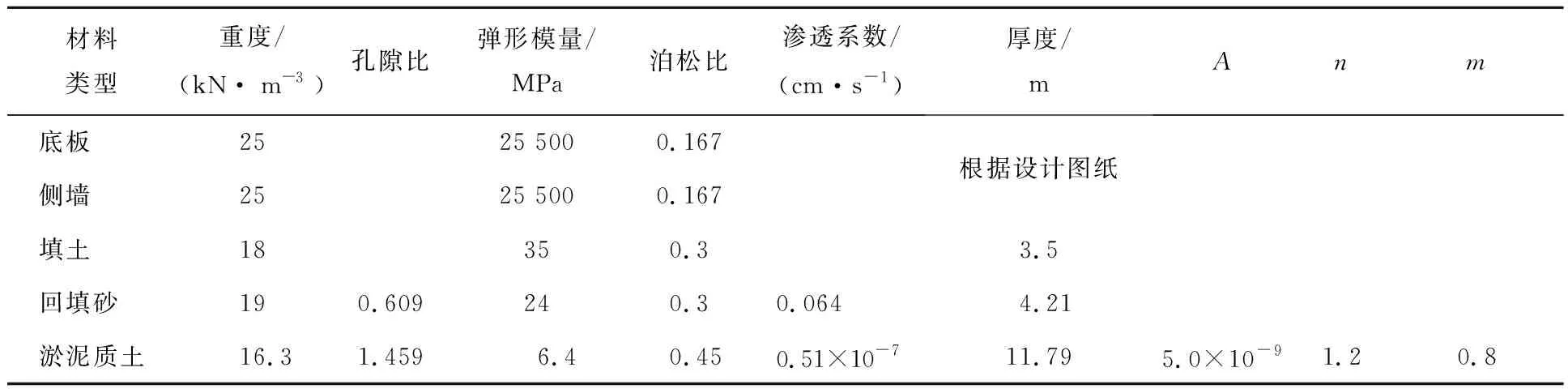
表3 土层物理力学参数

3.4 计算结果分析

图5为出水池地基表面测点2沉降量计算值和实测值随时间的对比关系曲线，从图5可以看出,道路运营1 a后，测点2计算最大沉降量为108 mm，与实测结果104.5 mm非常接近，偏差仅为3.5 mm，可见有限元计算沉降曲线与实测沉降曲线吻合较好，说明考虑蠕变-固结耦合效应的软土地基沉降计算结果符合实际情况，可用于进一步分析水池地基沉降变形的相关性状。

图5 测点2地表沉降量曲线

道路施工期间(0～12 m)，沉降量计算值表现为前期沉降速率较快，曲线较陡，且大于实测值，后期沉降计算值小于实测值。这是由于数值分析中假设荷载为线形施加，而实际施工过程中并非如此。

道路运营期间，与实测值相比，计算值偏大，这一现象在道路运营后期表现尤为明显。主要因为数值分析中土体参数是预先设定的，模拟施工中并未考虑土体参数的变化，实际上土体在固结过程中渗透系数和压缩性在不断降低。

图6为出水池地基表面测点1和测点2从道路拓宽施工到道路投入运营18个月的沉降曲线，分为道路施工和道路运营2个阶段。从图6中可以看出，计算得到地基表面测点1和测点2的总沉降量，分别为55.3，115.2 mm。

图6 测点1，2地表计算沉降量曲线

道路运营12个月后，沉降速率明显变慢，沉降曲线趋于稳定。道路施工结束时，测点2地基表面沉降量为87 mm，占总沉降量的79%。由此可见，出水池地基沉降主要发生在道路施工期。

3.5 孔隙水压力分析

超静孔隙水压力是反应软土地基固结状态的一个重要指标[18]。地基中的孔压测点布置方案如表4所示，根据有限元计算结果，表5给出了各测点超静孔隙水压力的消散速率和最大值，图7～8给出了从道路施工到投入运营18个月后，不同测点超静孔隙水压力随时间的变化曲线。

表4 孔压测点布置方案

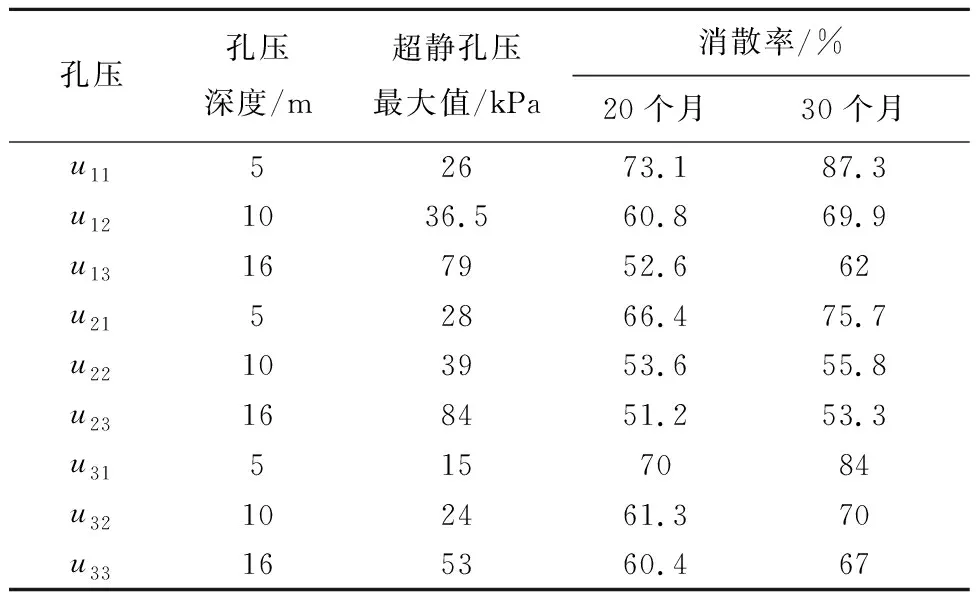
表5 各测点超静孔隙水压力变化

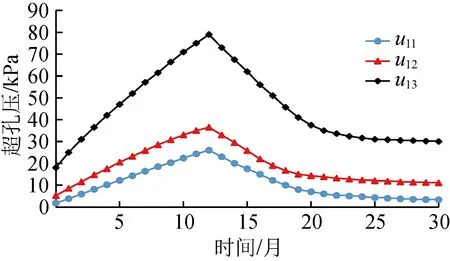
图7 测点1孔压变化曲线

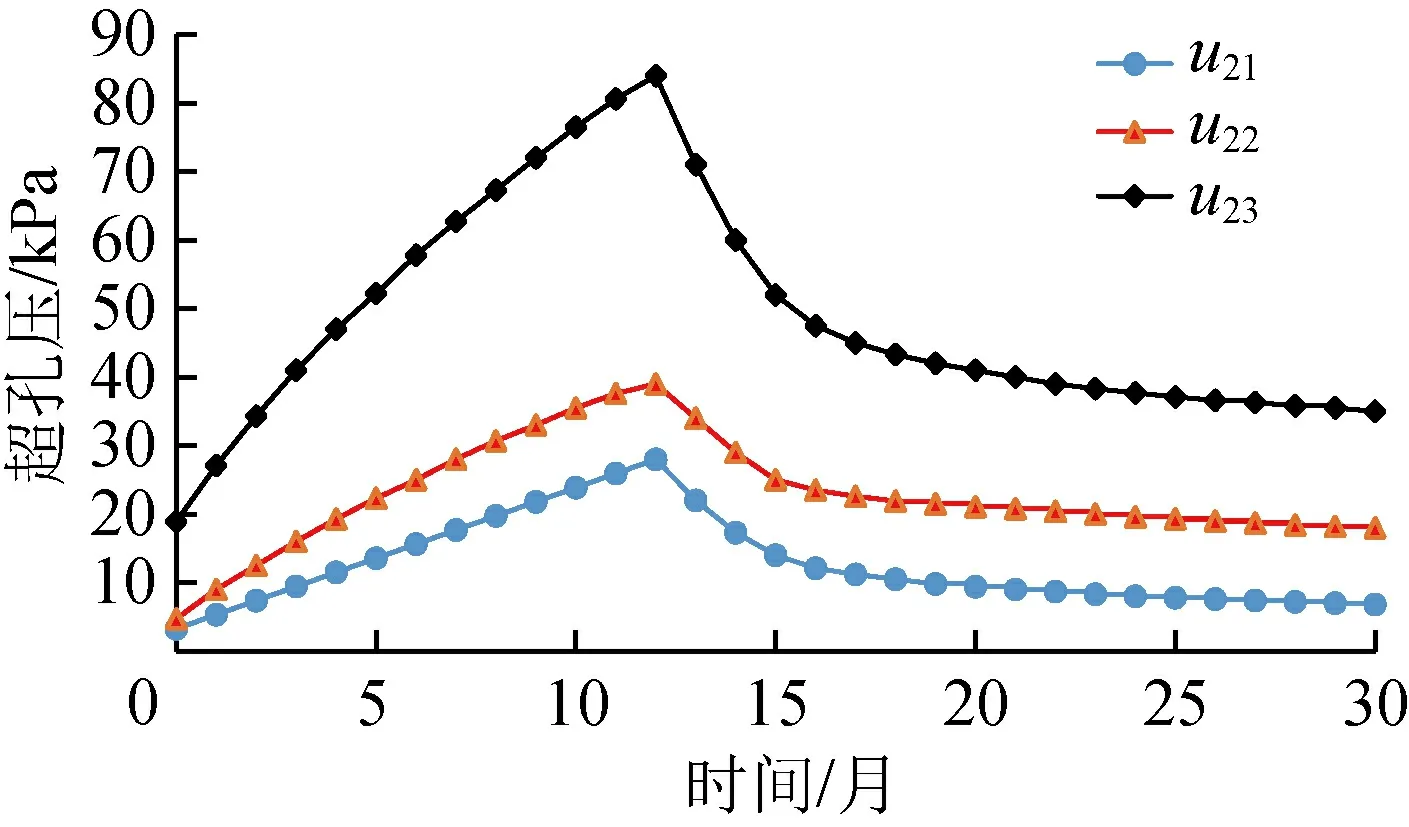
图8 测点2孔压变化曲线

由表5和图7～9可知，超静孔压最大值发生在地基下部土层即淤泥质土层中，并且在同一测点处超静孔压随深度增加而增大，这主要是因为上部回填砂固结系数较大且距离排水面较近，而淤泥质土层固结系数较小且排水路径较长；随着道路拓宽改造的进行，出水池地基邻近超载值不断增加，地基土体中的超静孔隙水压力显著增大，地基土体距离拓宽道路越近，超静孔压增大越明显。

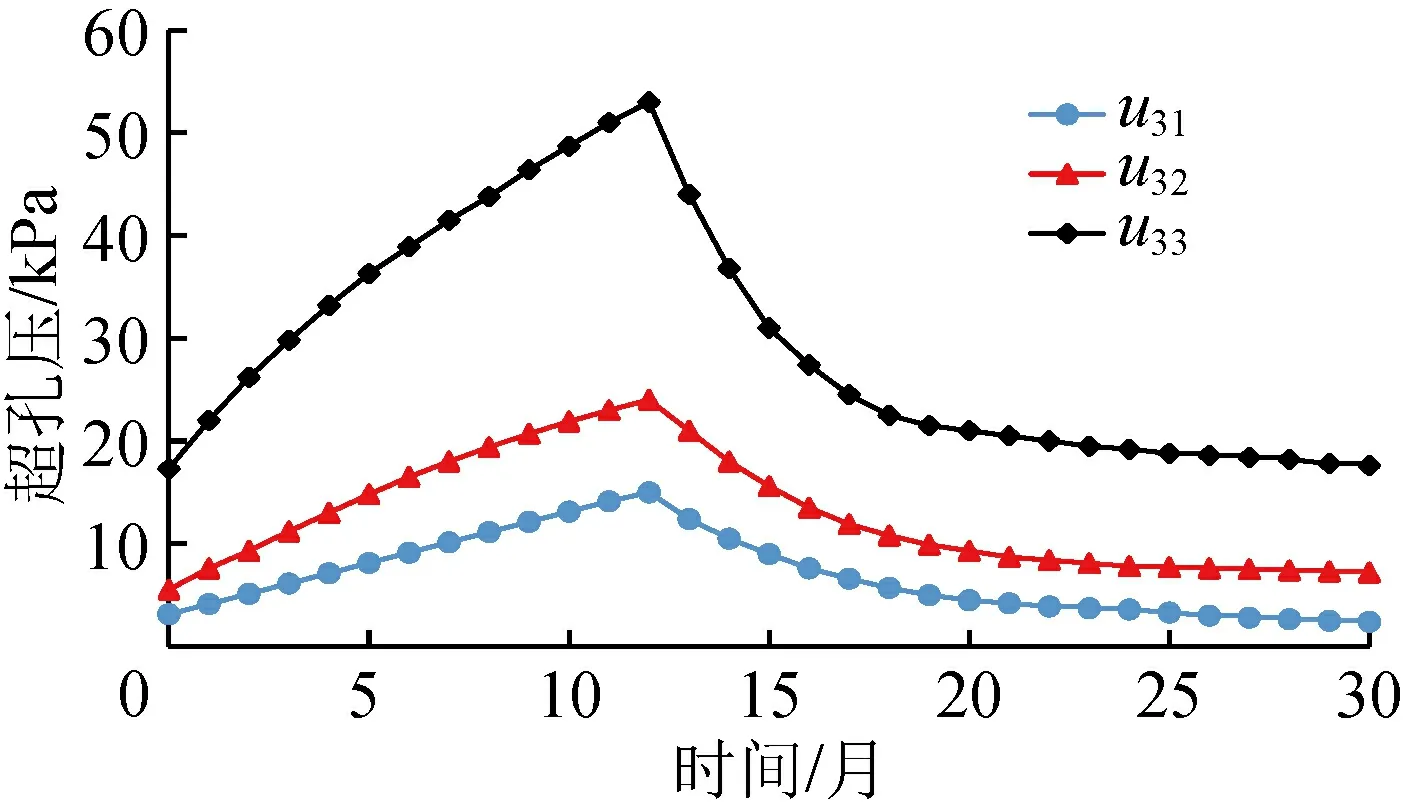
图9 测点3孔压变化曲线

道路投入运营后，超静孔隙水压力开始消散。超静孔隙水压力在道路投入运营后的前8个月消散速率较快，此后消散速率减慢并在运营12个月之后逐渐趋于稳定，这也与前面的沉降分析相一致。此外，由图7～9可知，在软土地基同一深度处，越靠近拓宽道路的土体，其超静孔隙水压力消散值越大，消散速率越小；在同一测点处，地基上部土层超静孔隙水压力消散较快，消散率较大，土体固结作用较强。

4 太沙基一维固结理论计算

4.1 理论计算

为进一步验证在软土地基沉降计算中同时考虑蠕变效应和固结效应的合理性，以便准确预测出水池地基沉降发展趋势[19-20]，本文结合2012版规范推荐的沉降计算公式和太沙基一维固结理论，计算地基土层变形量与时间的相互关系。相关计算参数见《排涝站岩土工程勘察初步报告》和《排涝工程(西片)初步设计报告》，并参考福州市区地基土层物理力学性质指标统计表确定。计算公式为[21]

S

(1)

式中：Ki为矩形面积上均布荷载作用下中心点下沉降系数，根据查表确定；ψs为沉降经验修正系数；p0为基础底面附加应力；Esi为第i分层土的压缩模量。

St=S∞·Ut，

(2)

Nt=π2Cv/(4H2t)，

(4)

式中：S∞为土层最终沉降量；St为某时刻t的土层变形量；Ut为地基土固结度；t为时间；Nt为时间因素；Cv为固结系数；H为土层的计算厚度。

4.2 结果分析

对比分析一维固结理论计算结果与数值模拟结果，由图10可以看出，不同工况下采用有限元法计算得到的地基沉降变形规律一维固结理论计算结果大致相似。但在相同时间点上，采用固结理论计算结果大于考虑软土流变性的数值方法计算结果。这是因为忽略了土体的流变性，研究表明，软土的流变特性和固结特性是相互影响的。流变性会影响孔隙水压力的消散，减缓固结效应，并且渗透系数越小，影响越明显。反之，固结作用又可以弱化流变现象，使土体的黏滞流动性降低。采用太沙基一维固结理论计算时，由于忽略土体流变特性对固结作用的影响，导致理论计算结果较有限元计算结果偏大。对比分析实测值、模拟值和计算值可知，在软土地基的沉降计算分析中，考虑软土的蠕变效应是有必要的。

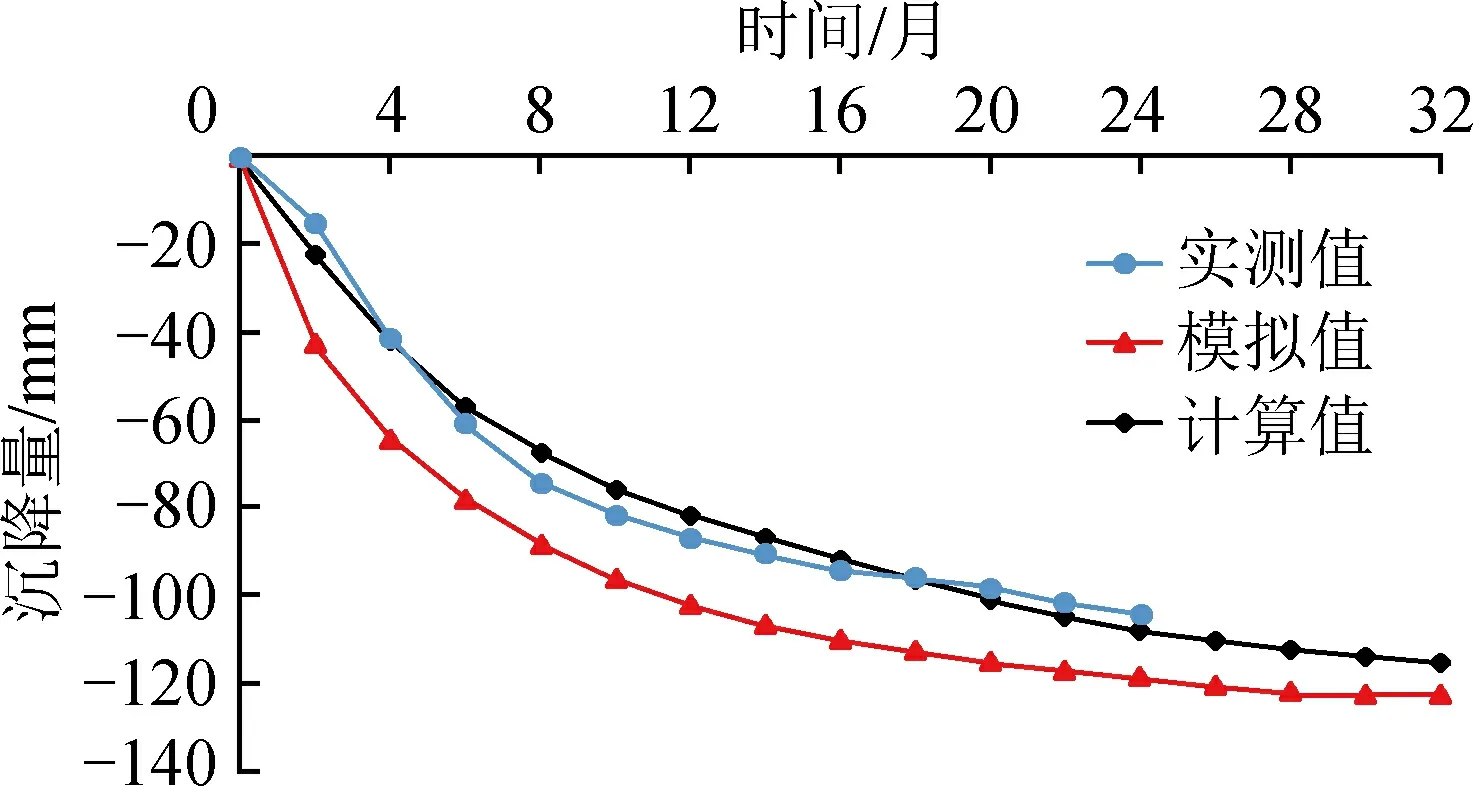
图10 地表沉降曲线对比分析

5 结 论

(1)道路施工期，出水池地基沉降量随时间增大而增大。施工结束后，随着时间增加，沉降速率放缓，沉降趋于稳定。不同测点处沉降量变化较大，沉降不均匀，最终导致出水池结构出现裂缝，影响出水池正常运行。

(2)采用ABAQUS有限元软件考虑软土蠕变-固结耦合效应的沉降计算结果与沉降实测值基本吻合。计算值与实测值最大沉降量偏差仅为3.5 mm，说明采用有限元软件计算邻近软土地基沉降具有现实意义。基于一维固结理论的规范法计算结果与计算值和实测值相比偏大，在软土地基的沉降计算分析中，考虑软土的蠕变效应是有必要的。

(3)道路拓宽施工对邻近软土地基沉降影响显著，实际工程中通过对拓宽道路的施工条件、施工方案的预先分析，确定附加荷载的类型和大小，进而利用有限元软件预测软土地基的沉降变形，避免邻近已有建筑的破坏，为以后类似工程的施工提供参考。