基于极限学习机的变压器热点温度实时预测方法研究

甘景福，马明晗，李永刚

(1.国网冀北电力有限公司 唐山供电公司，河北 唐山 063000；2.华北电力大学 电力工程系，河北 保定 071000)

0 引 言

电力变压器是电力系统输配电中重要的电气设备，它的安全、可靠、经济运行是人民生产和生活的重要保证。其中，变压器的热点温度直接影响着变压器的运行安全和设备寿命。因此，国内外有关变压器热点温度计算和预测的研究开展比较。

目前，变压器热点温度的获取方法主要可分为以下几类：直接测量法、导则计算法、热路模型计算法、数值计算法和智能学习法。直接测量法[1-3]主要是以在变压器绕组上预埋温度传感器的方式对热点温度进行直接测量，该方法对测点定位精度有要求，误差普遍较大；导则计算法[4-5]目前主要采用IEEE C57.91-1995和国标GB/T 1094.7-2008推荐的热点温度计算公式，这种方法类似于经验公式，得到的结果和实测数据差距较大；热路模型[6-7]计算法基于热传递理论和热电类比法，根据变压器传热参数及运行参数，建立变压器的热路模型，进而研究变压器的热特性，然而该方法得到的往往是热路模型的节点温度而不是热点温度，计算存在一定的误差；数值计算法[8-10]依据有限元理论，建立变压器的三维模型，进而对变压器整体温度场进行求取以获取热点温度，这种方法求解较为准确，但是需要变压器准确的设计数据和电磁参数，实现起来有一定困难；智能学习法采用变压器运行的历史数据或出厂实验数据，构建各变量与热点温度的关系模型，进而实现对热点温度的预测[11]，目前常采用的智能学习法主要有神经网络[12]、支持向量机[13-14]、卡尔曼滤波[15]、改进参数辨识[16]等，具有较强的容错能力和自适应能力，在工程中应用越来越多，然而，现有的一些基于智能算法的热点温度预测方法存在一定缺陷，一方面预测精度不能够保证，另一方面其模型运算速度慢，无法保证数据实时更新的要求。

极限学习机[17](extreme learning machine，ELM)是一种典型的单隐含层前馈神经网络算法。该算法输入层和隐含层间的权值以及隐含层的阈值是随机产生的，训练过程无需调整，只需设置隐含层神经元个数就可获得唯一最优解，具有学习速度快、泛化性能好的优点。算法一经提出便受到很大关注，目前已在故障诊断、负荷预测等领域内获得应用。

鉴于此，本文提出基于极限学习机的变压器热点温度预测方法。将变压器运行时的3个特征量(负载率、环境温度和顶层油温)作为输入变量[18]，绕组热点温度作为输出变量，构建ELM热点温度计算模型。建立基于支持向量回归的电力负荷预测模型，将预测结果作为ELM模型的前置输入，实现热点温度的实时预测。以某220 kV油浸式变压器运行数据为样本，用以验证基于极限学习机的变压器热点温度实时预测方法的有效性和准确性。

1 极限学习机

极限学习机2004年由南洋理工大学Huang提出，是一种典型的单隐含层前馈神经网络结构(single-hidden layer feedforward networks,SLFNs)，如图1所示。

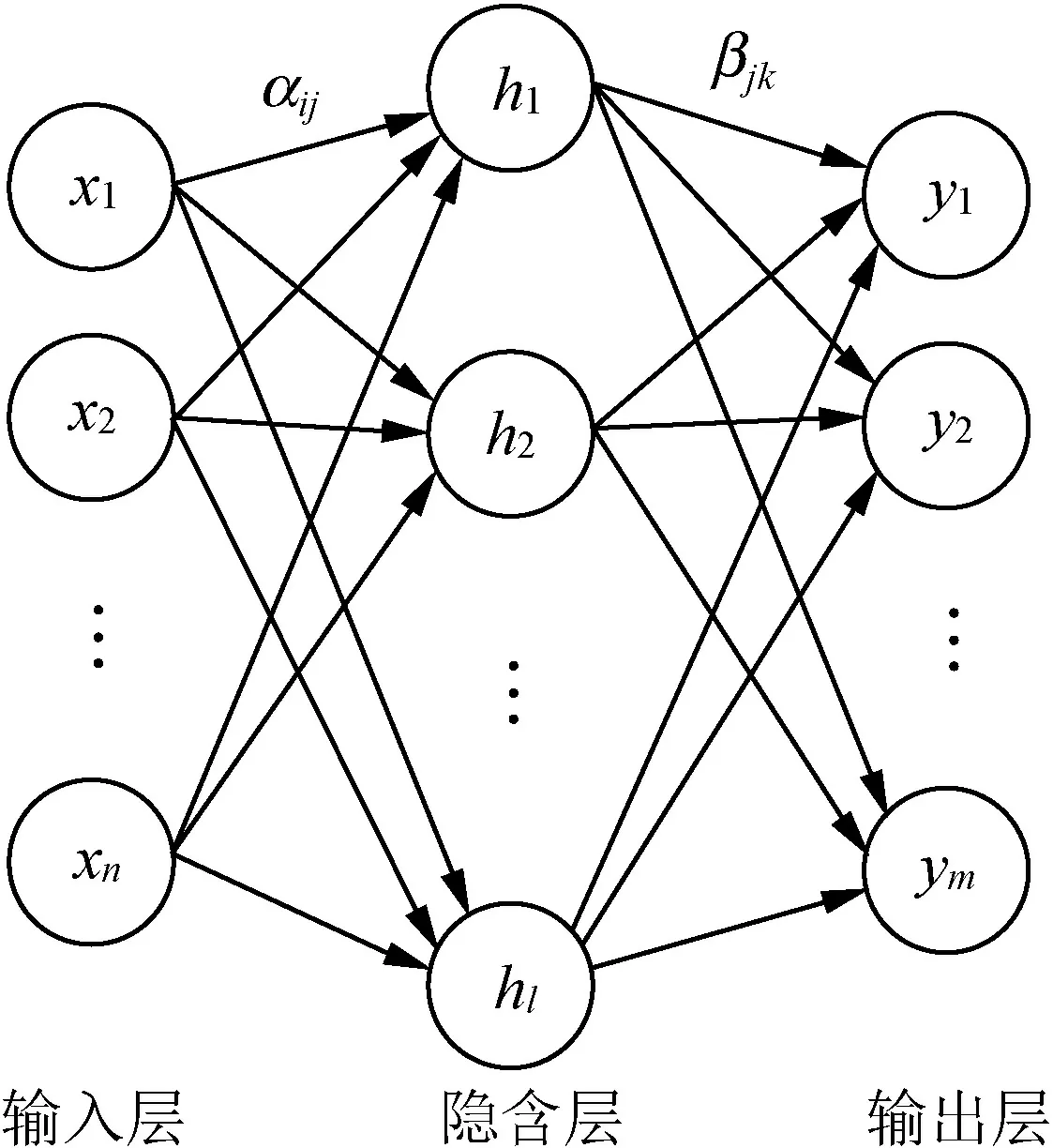
图1 单隐含层前馈神经网络结构

图1所示的神经网络包含输入层、隐含层和输出层，分别由n，l，m个神经元构成，αij为输入层第i个神经元与隐含层第j个神经元间的连接权值，βjk为隐含层第j个神经元与输出层第k个神经元间的连接权值。

输入层与隐含层间的连接权值为

(1)

隐含层与输入层间的连接权值为

(2)

设隐含层神经元的阈值为

(3)

设训练集有P个样本，则其输入矩阵E和输出矩阵O分别为

(4)

(5)

设隐含侧激活函数为G(x)，则神经网络输出为

(6)

(7)

式中，j=1，2，…，Q；αi=[αi1，αi2，…，αin]；ej=[e1j，e2j，…，enj]T。

式(7)可表示为

Hβ=TT,

(8)

H(α1,α2,…,αl,η1,η2,…,ηl,e1,e2,…,eQ)=

式中，H为隐含层的输出矩阵。

2 热点温度ELM计算模型

2.1 输入、输出层的选取

ELM模型的输入、输出由实际问题决定，对计算变压器热点温度θh可测且有价值的特征量为负载率K(负载电流I/额定电流IN)、环境温度θa、顶层油温θtop。因此，ELM模型的输入层和输出层分别为

x=[K,θa,θtop],

(10)

y=[θh],

(11)

输入层神经元数量n=3，输出层神经元数量m=1，热点温度ELM计算模型的输入/输出结构如图2所示。

图2 ELM输入/输出结构

2.2 计算模型

热点温度ELM计算模型的计算流程如图3所示。

(1)数据处理和划分。将实验采集的变压器负载电流、环境温度、顶层油温和热点温度数据按式(12)进行归一化处理，将每组数据处理成在[-1,1]之内，然后将数据样本随机生成训练集和测试集。

(12)

式中:x为待处理数据;xmax和xmin为该组数据的最大值和最小值，y为归一化后的结果。

(2)ELM创建和测试。由于前文已对ELM的输入和输出层进行了选取，创建过程主要是对隐含层神经元个数的设定和激活函数类型的选取。隐含层神经元个数可通过Kolmogorov定理确定，激活函数选取Sigmoid函数，然后将已划分好的样本数据进行训练和测试，构建出变压器热点温度的ELM计算模型。

(3)结果评价。计算算法运算时间，对训练结果进行反归一化，计算算法的拟合度，计算热点温度的计算值与真实值的误差平方和(SSE)、均方误差(MSE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)和均方百分比误差(MSPE)等多种误差分析指标，对模型的计算精度进行评价。

图3 变压器热点温度ELM模型计算流程图

3 试验结果与分析

本文以一台SFPSZ-180000/220型油浸式变压器为建模对象，该型变压器采用强迫油循环(OD)方式进行冷却。以350组温升试验数据和运行数据构成预测样本集，从中随机选取320组样本作为训练集，剩余30组样本作为测试集。

采用变压器热点温度ELM计算模型得到的计算值与实测值对比如图4所示。图4同时给出了计算值与真实值的绝对误差。可以看出，计算值与真实值差值在±4 ℃以内，具有较好的拟合度。

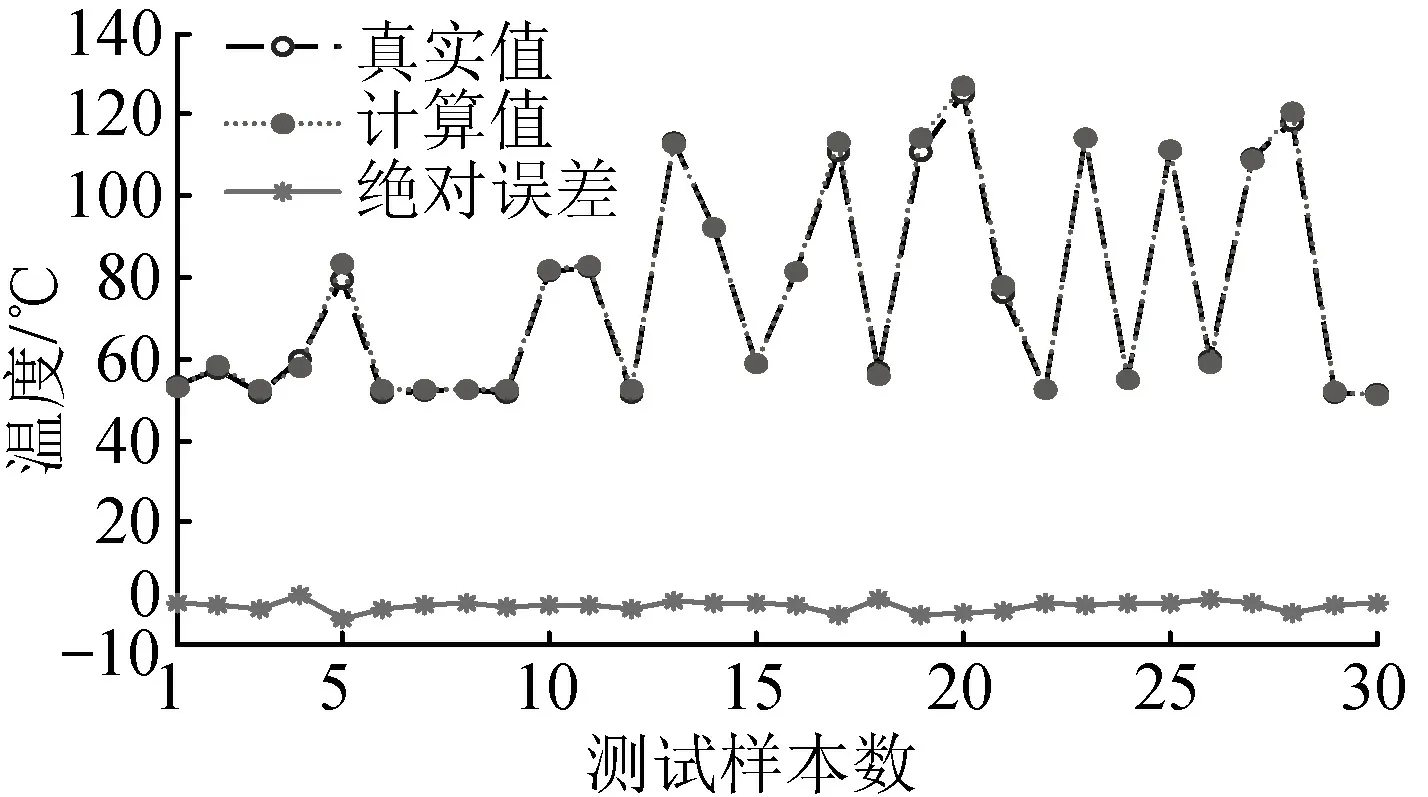
图4 ELM模型热点温度计算结果对比

为了比较不同热点温度计算模型的计算效果，将BP神经网络、Elman神经网络与ELM模型进行对比。表1为测试数据和不同方法的热点温度计算结果。

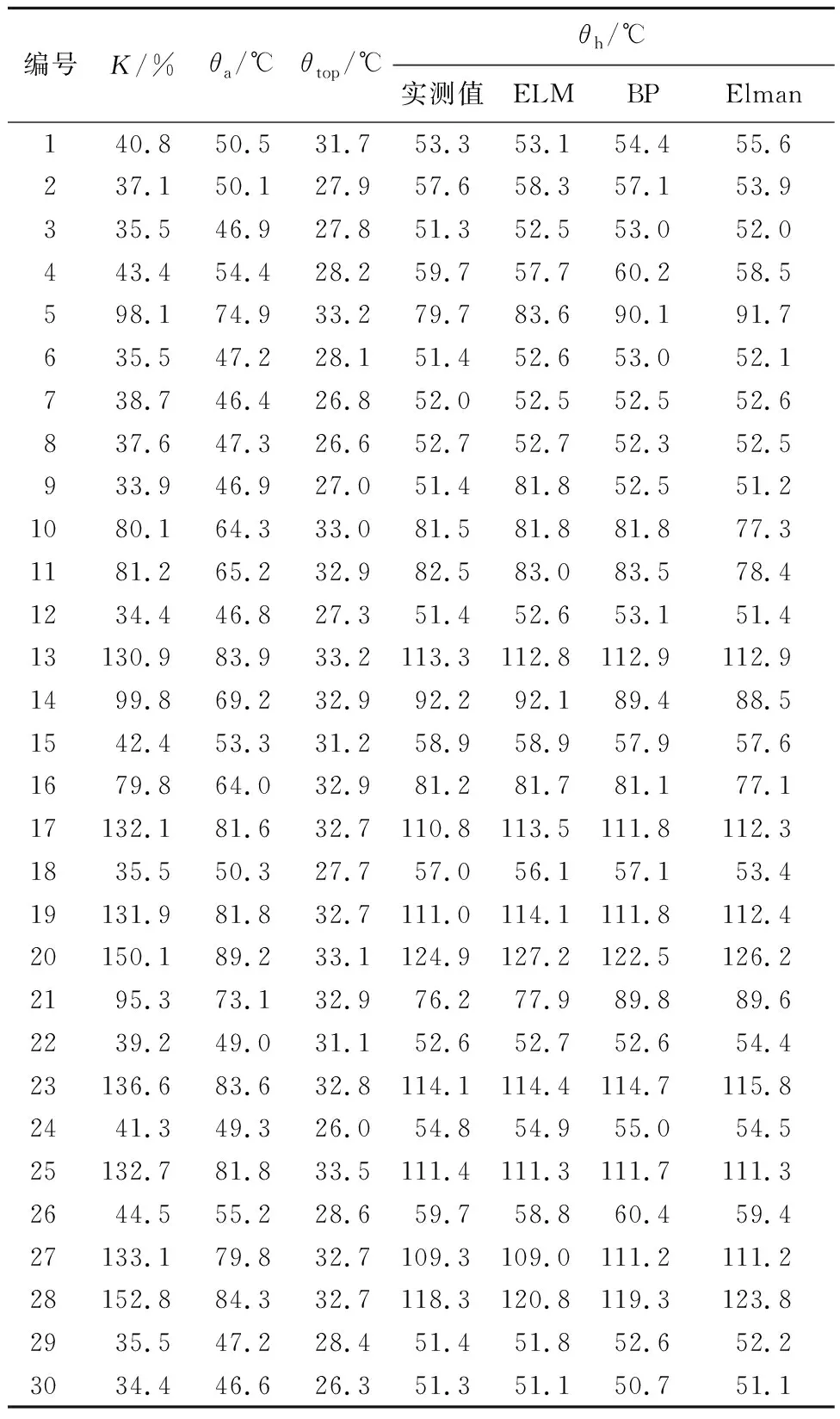
表1 测试数据和不同方法热点温度计算结果

图5和图6分别给出了BP神经网络和Elman神经网络热点温度计算值与实测值对比。

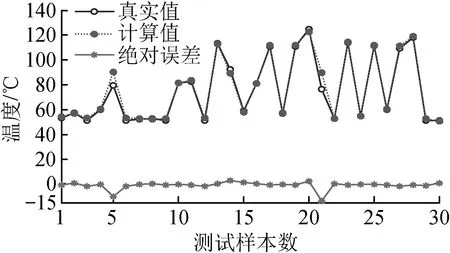
图5 BP神经网络热点温度计算结果对比

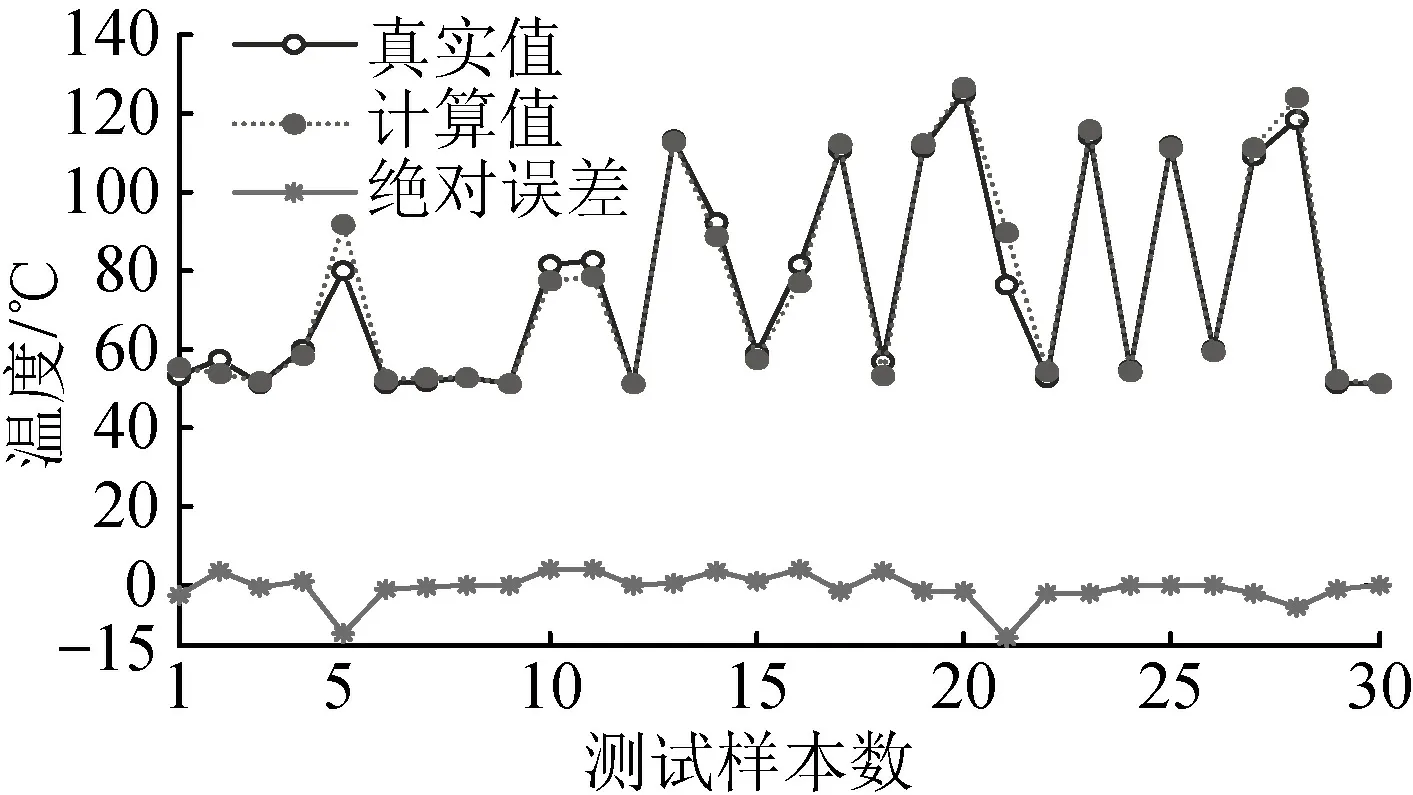
图6 Elman神经网络热点温度计算结果对比

为了对比热点温度3种计算模型的准确性，对3种方法的计算结果进行比较。图7为3种方法计算值与真实值的绝对误差情况对比。

图7 3种方法的绝对误差曲线

由图7可以更直观地看到，ELM模型较BP神经网络和Elman神经网络计算误差明显更小，准确度更高。BP神经网络和Elman神经网络虽然多数点的绝对误差与ELM模型类似，但个别数据点计算误差过大，计算准确度欠佳。

表2给出了3种方法的各项评价指标情况。

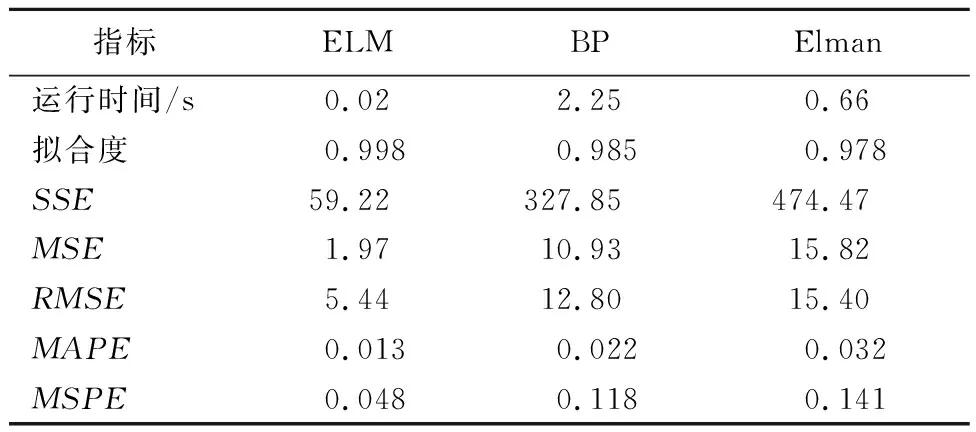
表2 3种方法的各项评价指标对比

由表2可见，ELM模型相比于BP神经网络和Elman神经网络，无论是在算法计算时间、拟合度，还是计算误差等各方面，指标都有着较大的优势。ELM模型的运算速度能够达到传统BP神经网络的100多倍，这对实现模型的实时动态调整有着重要意义。

4 热点温度ELM实时预测模型

如前所述，影响变压器热点温度的主要因素为负载系数、环境温度和顶层油温这3个特征量。环境温度在短期预测中基本可认为是不变量，而顶层油温跟随绕组温度的变化具有时间上的滞后性，短期内变化很小，因此，负载系数的准确预测是热点温度预测的关键。鉴于此，建立如图8所示的热点温度ELM实时预测模型。

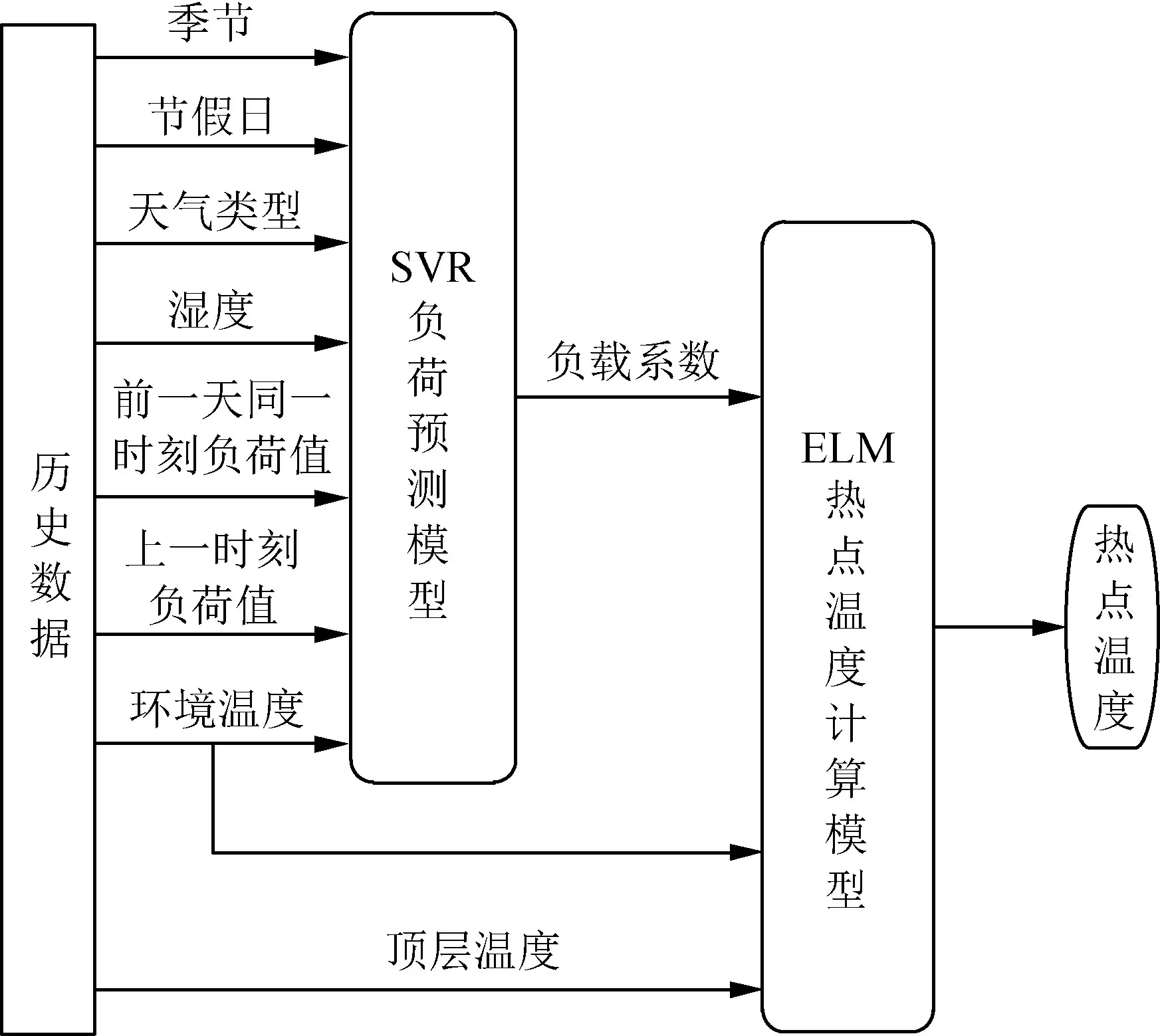
图8 热点温度ELM实时预测模型Fig.8 Real-time prediction model of hot spot temperature

由图8可知，热点温度ELM实时预测模型由2部分构成，即SVR短期负荷预测模型和热点温度ELM计算模型。其中，SVR短期负荷预测模型输入向量由7部分构成：温度，湿度，天气类型，季节类型，节假日，上一时刻的负荷值，前一天同一时刻的负荷值，输出向量为下一时刻负载系数，使之作为热点温度计算模型前置输入，代入实时重构的ELM热点温度计算模型，最终实现热点温度的预测。

选取某SFPSZ-180000/220型220 kV油浸式变压器2019年7月25日18:00至26日6:00热点温度为研究对象，采样间隔5 min。以7月25日18:00至22:00这4 h为训练样本，预测后1 h的热点温度数据，并实时更新训练样本，最终得到热点温度的预测值。预测值与实际值变化曲线如图9所示。

图9中，从热点温度ELM实时预测模型的预测结果看，其与热点温度真实值的误差在±1 ℃之内，具有很好的预测精度。3种方法的预测效果如表3所示，可见热点温度ELM实时预测模型具有更高的预测精度。与近期发表的文献[14，16]对比可知，热点温度ELM实时预测模型较PSO-SVM和CS算法的MSE值更小，计算精度更高。

图9 热点温度ELM实时预测模型结果对比Fig.9 Results comparisons of ELM real-time prediction model of hot spot temperature

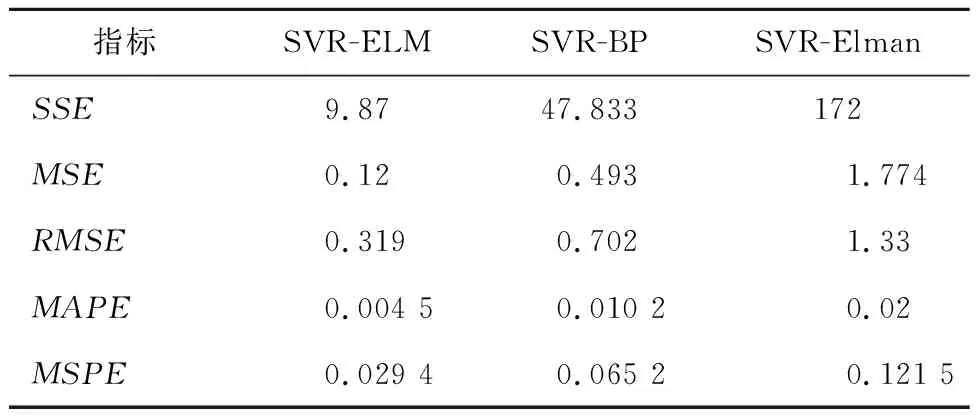
表3 3种方法的预测效果对比

5 结 语

提出了一种基于极限学习机的变压器热点温度预测方法。以变压器负载率、环境温度和顶层油温作为输入，绕组热点温度作为输出，构建热点温度ELM计算模型。以一台SFPSZ-180000/220型为例进行了试验研究，结果表明，该方法给出的热点温度计算值与真实值基本一致，具有很好的拟合度，且较传统的BP神经网络和Elman神经网络算法运算速度更快，便于模型的实时动态调整。通过构建基于支持向量回归(SVR)的电力负荷预测模型为热点温度ELM计算模型提供前置输入，实现了热点温度的预测并得到现场实际运行数据的验证，证明模型具有可行性和良好的预测精度。