小说中的数学趣题

华兴恒

杰克·伦敦是美国著名作家，曾在一篇小说里提过一道妙趣横生的数学题：主人公乘坐套了5条狗的雪橇从斯卡洛维伊赶回营地，在途中的第一个昼夜，雪橇全速前进。如果一直这样走下去，他能按时到达目的地。但是一昼夜后，2条狗扯断缰绳逃走了，剩下的路程只能靠3条狗拉雪橇走完，雪橇前进速度是原来速度的3/5，他到达营地的时间比预定时间迟了两昼夜。杰克·伦敦写道：“逃走的2条狗如能再拉雪橇走50英里，那么我就能比预定的时间只迟到一天。”看完这段文字，你知道从斯卡洛维伊到营地有多远吗？

这道题条件较多，数量关系也比较复杂，因此很多同学在解答时会觉得难以入手。其实，我们可以先从“逃走的2条狗如能再拉雪橇走50英里，那么我就能比预定的时间只迟到一天”这句话入手分析。如果5条狗拉雪橇全速前进50英里，主人公就比预定时间只迟到一天。根据题意，如果5条狗拉雪橇再全速行驶100英里，主人公就能按时到达目的地。再综合“一昼夜后，2条狗扯断了缰绳逃走了”的条件，我们可知主人公在第一天末离营地还有100英里。这100英里由3条狗拉雪橇走完，速度是原来速度的3/5，到了预定时间，主人公只能走完这100英里的3/5，即60英里。剩下40英里，3条狗还须在2天内拉着雪橇走完，即以全速的3/5每天走20英里，所以全速为每天走约33.3英里。由此可知，从斯卡洛维伊到营地的距离是33.3+ 100 =133.3英里，即214.5千米。

俄国著名作家列夫·托尔斯泰在一篇文章中讲述了一个悲剧故事。

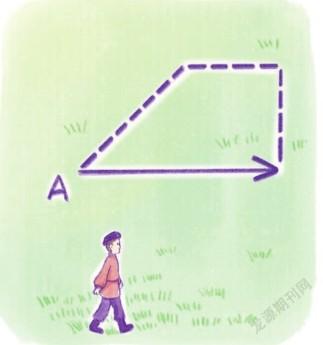
主人公巴赫姆到草原上买地，卖家这样规定：不论谁来买地，只要交1000卢布，就可以从一点出发，在一天内沿任何路线从日出走到日落，如果按时回到了出发点，那么这个人所走的路线围成的土地都归他所有；如果没有按时回到出发点，那这个人一点土地也得不到。

巴赫姆交了1000卢布，在第二天太阳刚升起时出发，在草原上朝某一方向快走了10俄里，才向左转弯，又快走了很长一段路程，再次向左转弯快走了2俄里。这时，他发现太阳快落山了，于是马上改变前进方向，向出发点奔去，终于赶在日落前跑了15俄里回到出发点。可是，当他回到出发点时，悲剧发生了——他两腿一软，跌倒在地上，口吐鲜血，死了。

根据这段情节，我们可以知道巴赫姆这一天走的路线能够围成一个直角梯形，从而可以计算出这个直角梯形的周长约为39.7俄里（约42.4千米），面积约86.7平方千米。

巴赫姆得到的土地并不算多，人却一命呜呼了。如果他懂得一些数学知识，其实能得到更多土地。巴赫姆走的路线若是正方形，圍成的面积约是112.4平方千米；若是圆形，围成的面积约是143.1平方千米。

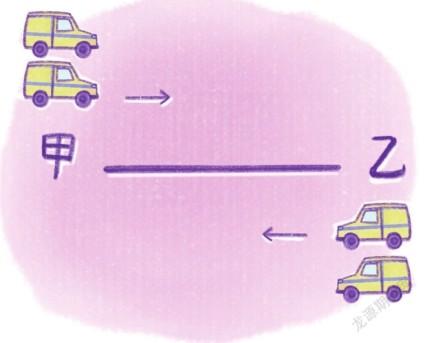
《奇婚记》是匈牙利著名作家卡·米克沙特的作品，书中有这样一道数学题：甲城与乙城之间有一条公路，每天从两座城市同时各驶出两辆邮车。一个人要从甲城到乙城去，搭乘一辆邮车，这辆邮车要行驶整整10天才能到达目的地。假定每辆邮车都以相同的速度在这条公路上匀速行驶，那么这个人坐邮车由甲城出发到抵达乙城，在路上会遇到多少辆迎面开来的邮车？

这是著名的“邮车相遇问题”。在解答这道题之前，我们必须明白：这个人在路上会迎面遇到两类邮车，分别是在他出发前和出发后从乙城驶出的。为了简化解题过程，降低探究难度，我们可以这样思考：这个人乘邮车由甲城出发之前的10天内，已有20辆邮车先后从乙城驶出，正行驶在路上。这个人乘邮车在路上行驶的10天中，又有20辆邮车先后从乙城驶出。当这个人到达乙城时，还将遇到2辆刚从乙城出发驶往甲城的邮车。因此，这个人一路上迎面遇到的邮车总数应是20 + 20 + 2 = 42。