构建中间需求模式的制造商最优产品供应策略模型

卓志毅，何 跃，阎 洪

（1.武夷学院商学院，福建武夷山 354300；2.泰国正大管理学院中国研究生院，泰国曼谷11120 3.四川大学商学院，成都 610065；4.香港理工大学专业及持续教育学院，中国香港 999077）

在消费品供应链领域，厂商通过顾客需求获取市场动态和顾客偏好，生产和销售满足顾客需求的产品，从而获取巨大的经济效益。在消费品供应链中，顾客需求是影响客户购买行为的基本驱动因素［1-2］。个人客户或集团客户这两种不同类型的客户通过购买、使用或消费商品和服务来满足其需求。因此，制造商不仅要考虑与生产技术创新相关的因素，如产品研发创新、新能源技术创新、科教融合创新，还要考虑影响消费者购买行为，顾客公民行为，不同类型客户的产品差异化的需求因素。零售商要考虑产品种类偏好、消费者购买行为等的需求因素。需求在产品供应链领域的研究一直是个热点话题之一［3-12］。然而，笔者对现有研究进行归纳总结发现［13］，现有研究忽视了管理实践中顾客需求真实存在的3 种不同的需求模式：本质需求模式、非本质需求模式和介于两者之间的中间需求模式。那么，本文首先要明确：这3 种需求的含义是什么？

科技日新月异的发展造就了社会生产力的进步，也造就了人们由原来的解决温饱问题变成了今天的满足精神需要。现如今，厂商生产的产品由于种类繁多、更新换代快等因素，故而在满足顾客需求上已经从原来的解决问题这种基本生理需求（本文称为本质需求）变革为以满足人们日益丰富的文化精神娱乐层面上的品位型需求（本文称为非本质需求）。在这里，本文举个简单的例子来验证本文的理论。从喝咖啡这样一个简单的真实案例可以看出，顾客需求可以分为2 种维度。第一层次的需求是本质的需求，也就是解渴的功能。因此，本文称为本质需求。但是，现如今的喝咖啡仅仅只是解渴这个本质功能吗？不是的，还有第二层次的功能，那就是社交的功能。和朋友邀约一起喝咖啡成了现代都市人的一种日常习惯，这时候的喝咖啡已经成为一种社交媒介，这种需求也就是非本质的需求，本文称为非本质需求。

此外，还有一种需求是介于本质和非本质之间的需求，本文称为中间需求，还是用喝咖啡这个案例来描述，那就是顾客因为口渴来喝咖啡，但是突然想到好久没有和朋友一起聚会了，就打电话约朋友一起到咖啡店相聚。这种消费者带着“真正有需要的需求”到达商店，面对一连串外来因素影响的信息，最终随着不断增加的外来影响因素，消费者被迫将需求分成不断更小的元素。这些既不是非本质的需求，又不同于客观上确定的“本质”需求，而是消费者在模糊不稳定的状态下形成“需求”的物质和象征方面，就是中间需求［14］。本文认为，根据相关学者［15-16］的研究，这3 种需求模式的划分，是以它的类别属性为依据。以喝咖啡为例，因为口渴而喝咖啡，这是它的本质功能，这种功能侧重于实用性，这种属性的产品主要是人们生存需要的物质保证，对应的是本质需求；而喝咖啡引申的社交功能，则是它的非本质功能，这种功能侧重于品位性，这种属性的产品跟人类生存需要完全没有任何关系，是人类在满足生存需要后追求更高的精神享受的产品。因此对应非本质需求。中间需求则是既有本质需求的属性，例如，咖啡的基本功能是解渴，这些功能都是保障人类生存需要的基本功能；同时又有非本质需求的特征，例如，咖啡的更深层次的功能是社交、工作的功能，这些功能是人类在满足生存需要后追求更高层次的精神需求的一种意识形态和社会文化过程。从现有产品的阵容上看，同时具有本质需求属性和非本质需求特征的中间需求的产品是客观存在的，而且产品种类和数量不少，对它的划分也是必不可少的。用一个形象的比喻来分析这3 种需求模式的产品，那就是在军队中有不同的兵种肩负不同的作战任务，如海军主要承担海上作战任务，空军主要承担空中作战任务，陆军主要承担陆上作战任务等［17］，而在产品阵容上也需要有不同的产品行使不同的市场职能，各个不同类型的产品相互配合、系统作战，充分迎合或引导消费者的购买心理和购买行为，从而通过产品类型定位实现最有竞争力的价格体系优势和产品功能优势，为企业的发展保驾护航，进而实现企业的战略目标。因此，为了更好地达到精准营销的目的，制造商在针对不同类型的客户制定不同的产品供应策略时，还是需要对顾客需求细分为本质需求、非本质需求和中间需求。

经过深入分析，本文发现，大到买房买车小到喝咖啡喝茶这种日常习惯，顾客需求都存在两种以上的维度，可以说，意识形态因素逐渐成为影响消费者购买行为的主流因素。Marcuse［18］的研究表明，一切不是为了产品的本质目的，而是全凭经济利益、心情好坏或广告宣传等外部环境影响购买行为的需求是“虚假的”需求，也就是本文认为的非本质需求。但是，本文并未发现现有研究有关于产品的顾客需求可以分为多个维度（顾客的本质需求、顾客的非本质需求和顾客的中间需求），并对这些维度进行分类别研究（即顾客需求的不同模式）的成果。与此同时，史雁军［19］将顾客分为两种类型：个人客户和集团客户。它们两者之间的区别在于集团客户的采购量较大，需求量也比较大并且需求较为稳定，而这个因素的实质就是批量折扣。因此，只需在个人客户的基础上增加一个折扣的决策变量。这表明，研究个人客户的产品供应策略问题显得更为重要。综上，产品制造商和零售商如何根据顾客需求的不同模式和不同类型的客户设计和规划不同的产品供应策略成为现有研究的一个重要理论缺口。本文研究的是制造商在中间需求模式下为个人客户设计和规划产品供应策略，这一研究填补了消费品供应链领域中的一个重要理论空白点，具有一定的理论研究价值。

一、变量函数

（一）中间需求函数

Petruzzi 和Data［20］把需求看作是价格的随机函数。因此可以用加法或乘法的形式来对需求函数进行建模，加法形式表示的是一种现象需求曲线，而乘法形式表示的是一种弹性需求曲线。Mills［21］利用加法形式将需求函数定义为D（p，ε）=y（p） +ε的函数模型。Karlin 和Cair［22］利用乘法形式将需求函数定义成D（p，ε）=y（p）ε的函数模型。这两种D（p，ε）属于经典的需求函数模型，在经济学的定价文献中很常见，并且应用较为广泛。这个模型表示市场需求曲线的形状也是确定的，而市场规模的尺度是随机的。但是，这两种需求函数的定义都是直接根据整个顾客群来定义的，无法探析顾客需求背后的原因，更无法实现精准营销的目的。为此，本文必须根据3 种不同需求模式进行划分，对原来的需求函数进行改进。结合3 种需求模式的不同侧重点，以及陈圻和王强［23］将商品的属性功能划分为实用功能和品位功能，并由此构造的效能函数这一结果，本文将需求函数模型推广到本质需求［24］、非本质需求［25］和中间需求［26］的函数取值范围，并定义了中间需求函数的表达式：

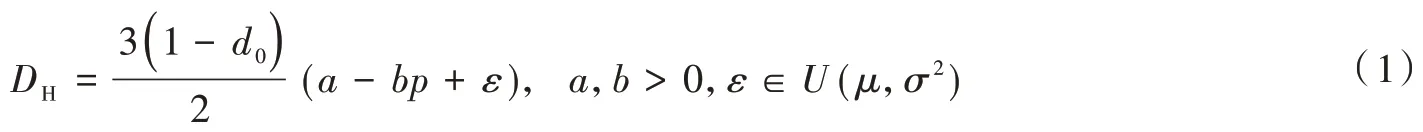
其中：DH表示中间需求函数；d0表示产品实用效能权重的最小值；a和b表示产品的销售量系数；p表示价格；ε表示误差系数。

正态分布和均匀分布虽然在结果上会呈现不同的差异，但是在本质上的函数模型建模思想是一致的。因此，为了便于研究，本文设ε为在区间[-（a-bp），a-bp]上服从均匀分布的函数，得：

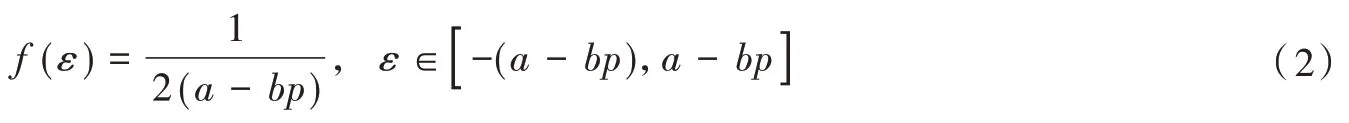
（二）制造商利润函数

制造商将产品批发给零售商或直销给个人客户或集团客户，这一过程必然存在生产的产品的供应量大于需求量或供应量小于需求量两种情况。本文假设制造商生产某种产品的边际成本为c，若是生产q单位的产品，则可得到生产某产品的总成本为cq，假设需求量为D（p，ε），每单位的产品批发价为p。这时，如果供应量小于需求量，产品可以全部销售出去，相应的总销售收入为pq；如果供应量大于需求量，本文发现制造商针对这款产品的销售收入仅为pD（p，ε），还有一部分库存产品不能售出（本文简称“剩余量”）。这时候，制造商为了尽快回笼资金，会想办法将这部分库存产品销售出去。假设制造商对剩余量q-D（p，ε）按照每单位h元的费用进行折价处理，又设该折价部分每单位的损失费用为S。因此，本文定义了制造商的利润函数为

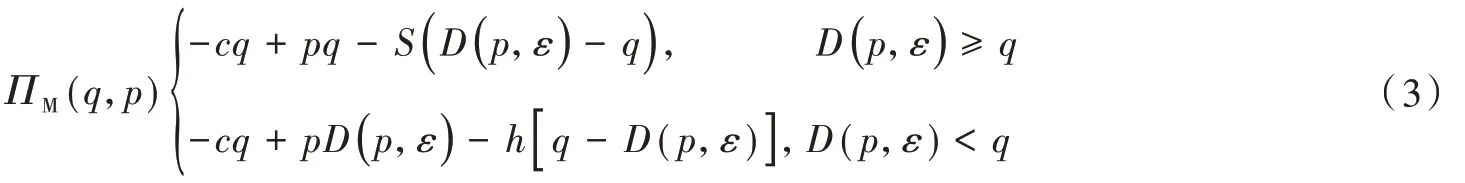
二、基于中间需求模式的制造商产品供应策略模型

本文通过构建2 个数学模型来表示中间需求模式下的制造商对个人客户设计和规划产品供应策略：直接折扣模式和未售出处理模式，并对制造商在这两种供应模式中获取最大利润时分别对应的最优生产量q、最优定价p进行求解。在模型求解之前，首先对相关变量进行定义：0～2()a-bp表示制造商生产量的范围，d0表示产品实用效能权重的最小值，p表示制造商向个人客户直销的产品零售价，q表示制造商的生产量，α表示制造商给个人客户的再优惠，c表示制造商的边际成本，γ表示制造商打折处理的费用。

（一）直接折扣模式下产品供应策略模型

在这种供应模式下，本文假设制造商生产某种产品的边际成本为c，生产q单位产品的总成本为cq，制造商直销给个人客户的零售价为p。在实际销售中，供给双方都会对价格展开价格协商，最终制造商为了促进销售，尽快回笼资金，决定对每个产品的零售价再优惠α。这时，如果制造商的生产量大于需求量时，可以回笼的资金为(p-α)DH(p，ε)；如果制造商的生产量小于需求量时，那么产品可以全部销售出去，资金全部回笼为(p-α)q，由此可得制造商的利润为

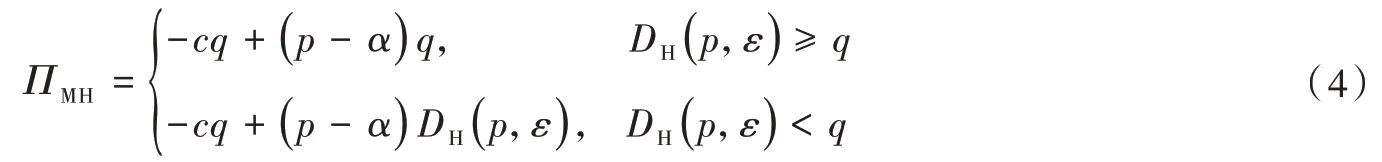
将式（1）代入式（4）可得：

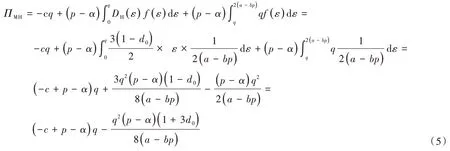
对式（5）的两边分别关于p，q求一阶导数，并令其所得的一阶导数为0。可得该模式下的最优生产量q和最优定价p。

求该模式下制造商的最优生产量q，只需对式（5）的两边同时关于q求一阶导数，并令其为0，可得：

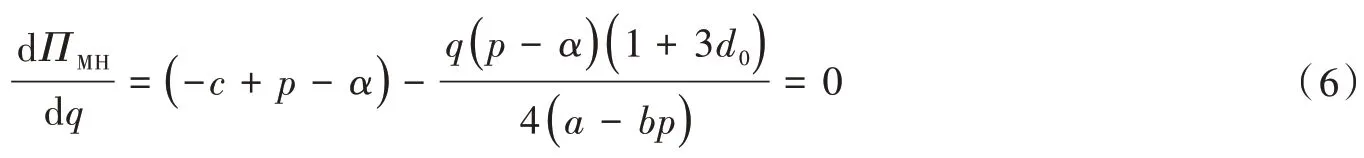
解式（6）得到的q值即为制造商的最优生产量。

求该模式下制造商的最优定价p，只需对式（5）的两边同时关于p求一阶导数，并令其为0，可得：

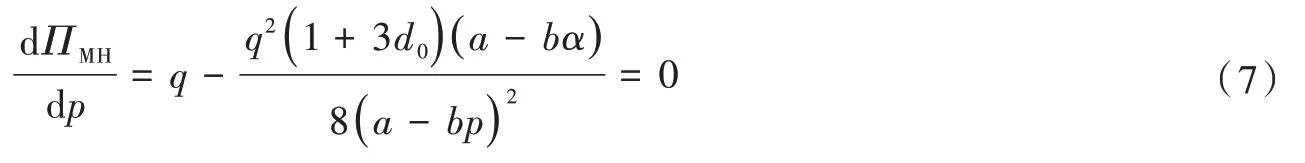
解式（7）得到的p值即为制造商的最优定价。

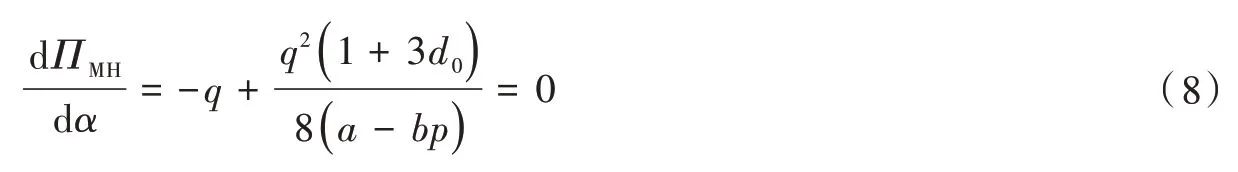
解式（8）得到的α值即为制造商的最优让利。

（二）未售出处理模式下产品供应策略模型

在这种供应模式下，制造商为了尽快回笼资金。因此对于未能销售出去的库存产品进行折价处理。本文假设制造商生产产品的边际成本为c，生产量为q，此时制造商生产产品的总成本为cq。如果制造商的生产量大于需求量时，产品的总销售收入仅为pDH(p，ε)，对于剩余量q-DH(p，ε)还要进行折价处理，对于这部分产品，本文设制造商给予产品的折价处理费用为每单位γ，由此可得制造商的总销售收入为pDH(p，ε)+γ[q-DH(p，ε)]；如果制造商的生产量小于需求量时，产品可以全部售出，那么销售的总收入为pq，由此可得制造商的利润为

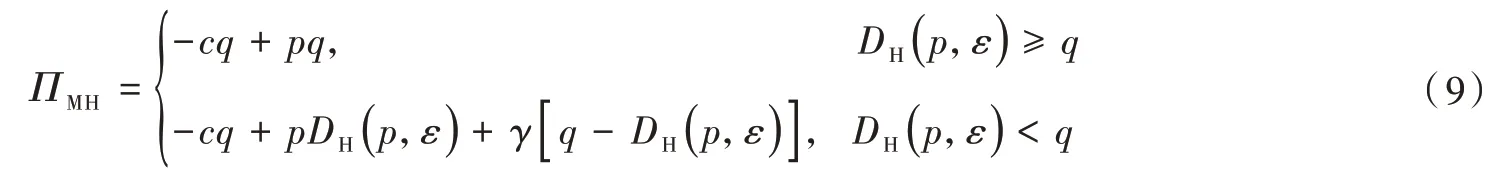
将式（1）代入式（9）可得：

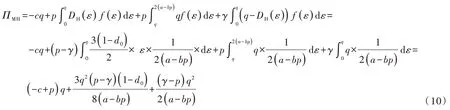
对式（10）的两边分别关于p，q求一阶导数，并令其所得的一阶导数为0。可得该模式下的最优生产量q和最优定价p。

求该模式下制造商的最优生产量q，只需对式（10）的两边同时关于q求一阶导数，并令其为0，可得：

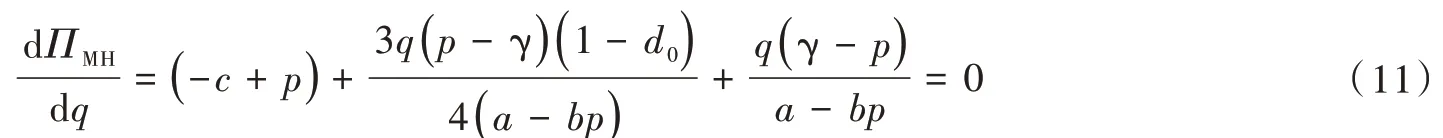
解式（11）得到的q值即为制造商的最优生产量。

求该模式下制造商的最优定价p，只需对式（10）的两边同时关于p求一阶导数，并令其为0，可得：

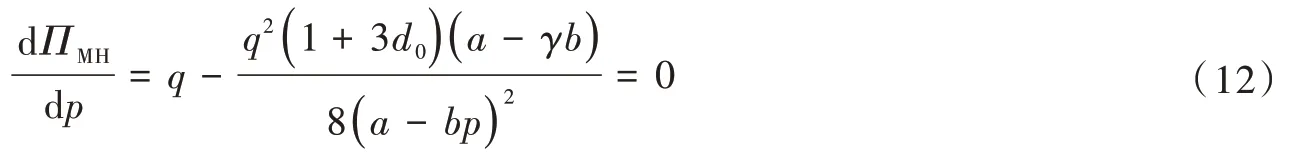
解式（12）得到的p值即为制造商的最优定价。

三、算例分析

本文的理论贡献在于构建了中间需求模式下的制造商最优产品供应策略的函数模型，跟现有研究相比，这个模型从理论上构建了中间需求在真实场景上的应用。但是根据上述方程式，本文发现制造商在中间需求模式下对个人客户的产品供应策略的数学模型中变量关系非常复杂，最优生产量（销售量）q∗和最优价格p∗均没有显式解。因此，为了验证模型是否真实反映中间需求模式下的产品供应策略这个现实问题，本文将通过数值算例的方式检验模型的有效性。

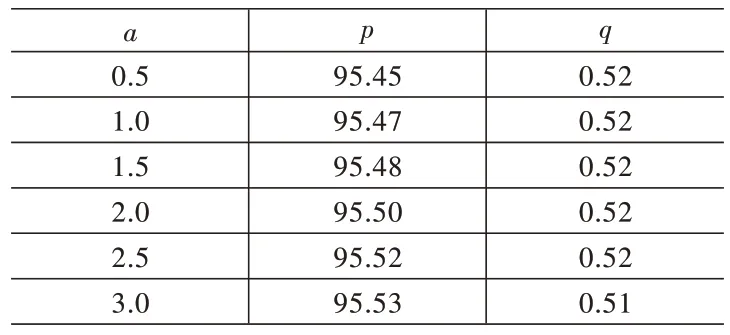
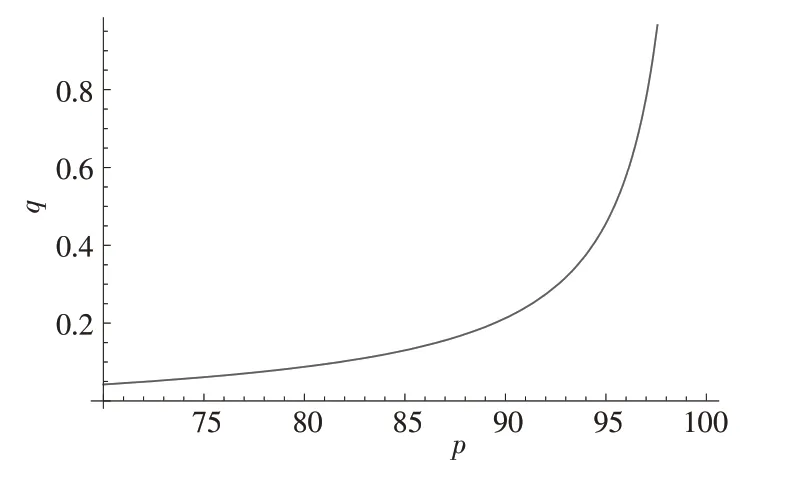
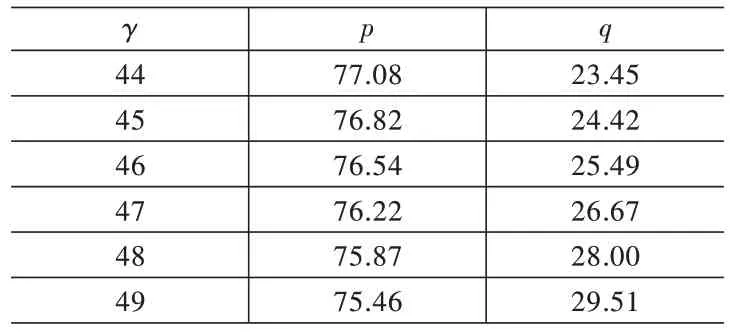
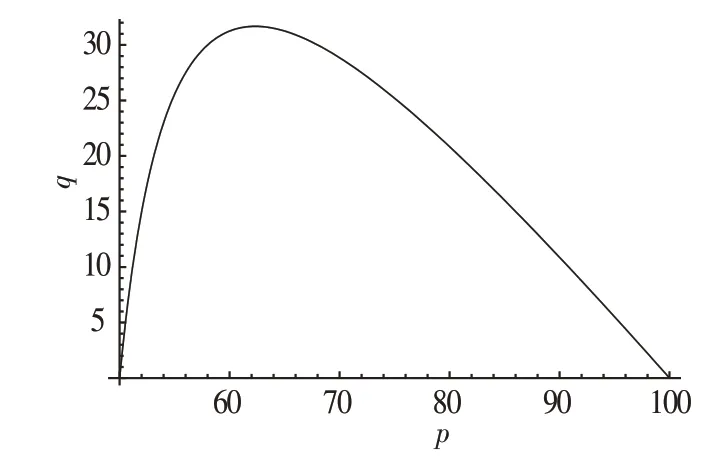
假设某制造商计划生产和销售一款普通产品，设这款产品单个的生产成本为50，如果生产量大还能进一步降低成本，又设市场上该产品当前的最高零售价为100，此时制造商向个人客户直销的产品零售价需要满足50

本文考虑生产量对价格和收益的影响，设基本参数如下：a=50，b=0.5，c=50，d0=0.2。

（一）直接折扣模式下的制造商‐个人客户产品供应策略

假设制造商生产一个产品的边际成本为c，生产q单位产品的总成本为cq，制造商直销给个人客户的零售价为p。假设对个人客户直销供货时，为了促进销售每个产品再优惠α。倘若制造商的生产量大于需求量时，只能回收成本(p-α)DH(p，ε)；倘若制造商的生产量小于需求量时，则可将产品全部售出，回收(p-α)q。与此同时，本文为了检验制造商对个人客户的再优惠α对最优生产量和最优价格产生何种影响机制，本文将对α在区间（0.5，3）范围内并以0.5 的递增进行数值计算。

运用Mathematica 8.0 将设置的基本参数代入式（6）和式（7）进行求解，可得制造商的最优生产量和最优价格。

数值计算表明，在直接折扣销售模式下，满足约束条件50

本文通过Mathematica 8.0 的制图功能将表1 推广到图1。由图1 可知，在直接折扣模式下，最优定价与最优生产量的关系呈抛物线关系，抛物线呈向上趋势的最高点即为制造商的最优定价。根据Pukelsheim［27］的三西格玛准则定理，制造商对个人客户销售的产品定价在区间（95，96）范围内，制造商的利润可以达到现实状态下的最大化。根据最优化理论原理，此时制造商的利润达到最优。

表1 直接折扣模式下的最优生产量和最优价格

图1 直接折扣模式下的制造商最优定价随最优订货量变化趋势图

（二）未售出处理模式下的制造商‐个人客户产品供应策略

在这种供应模式下，对于制造商未能销售出去的产品进行打折处理。假设制造商以边际成本为c的进行产品的生产，生产量为q，此时制造商的总成本为cq。倘若制造商的生产量大于需求量时，只能回收pDH(p，ε)，对于剩下的q-DH(p，ε)还要进行处理，对于这部分产品，制造商给予打折处理花费为每单位γ，则总回收价格为pDH(p，ε)+γ[q-DH(p，ε)]；倘若制造商的生产量小于需求量时，则可将产品全部售出，回收pq。与此同时，本文为了检验制造商的打折处理费γ对最优生产量和最优价格产生何种影响机制，本文将对γ在区间（44，49）范围内并以1的递增进行数值计算。

运用Mathematica 8.0 将设置的基本参数代入式（11）和式（12）进行求解，可得制造商的最优生产量和最优价格。

数值计算表明，在未售出处理经销模式下，满足约束条件50

为了更加直观地分析优惠值与最佳生产量、最佳定价的变化情形，本文通过Mathematica 8.0 的制图功能将表2 推广到图2。如图2所示，在未售出回收模式下，最优定价与最优生产量的关系呈倒向的抛物线关系，抛物线呈向上趋势的最高点即为制造商的最优定价。根据Pukelsheim［27］的三西格玛准则定理，制造商对个人客户销售的产品定价在区间（60，64）范围内，制造商的利润可以达到现实状态下的最大化。根据最优化理论原理，此时制造商的利润达到最优。

表2 未售出处理模式下的最优生产量和最优价格

图2 未售出处理模式下的制造商最优定价随最优订货量变化趋势图

四、结论

本文考虑了中间需求模式下的制造商针对个人客户的产品最优供应策略。在此研究过程中，本文针对顾客需求的不同模式，首次提出了除了本质需求和非本质需求模式之外的第3 种需求模式-中间需求模式。尤其重要的是，本文还结合Mills［21］的需求函数表达式及陈圻和王强［22］关于产品效能函数研究，定义了中间需求函数模式的函数表达式，并最终由此构造了中间需求模式下制造商的最优产品供应策略模型。

本文的主要研究贡献在于以下两个方面：一是本文的研究发现在消费品供应链领域顾客需求存在3 种不同模式，但是现有研究并未有这3 种不同模式的结果。因此本文的研究对于顾客需求在消费品供应链领域的应用具有一定的理论推进作用；二是现有研究并未考虑制造商或零售商在不同供应模式下的产品供应策略问题，而本文考虑了制造商在直接折扣模式和未售出处理模式两种不同供应模式下的产品供应策略，并通过数学模型验证了实现产品利润最优的最优定价和最优生产策略，在管理实践中具有一定的实践意义。在后续的研究中，本文将进一步考虑利用需求函数的乘法模型构建中间需求模式下的产品供应策略模型，并进行比较分析。