遥感图像的有向空间高斯混合模型分割方法

卢印举，段明义，苏玉

(郑州工程技术学院 信息工程学院，郑州 450044)

0 引言

图像分割是数字图像处理、计算机视觉领域中的基本问题之一，目前已取得了良好的应用成果，包括遥感图像分析技术[1]、磁共振成像(magnetic resonance imaging，MRI)技术[2]、合成孔径雷达(synthetic aperture radar，SAR)图像技术[3]以及目标检测技术[4]等应用领域。它主要是利用各类图像所具有纹理、颜色以及灰度等各方面的特征来划分图像，使各个区域展现出某一类特性。但是，在实际成像处理时，由于一系列因素包括场偏移效应、局部容积效应以及噪音等的影响，导致所采集到的图像出现了一些不同的特点，如复杂的场景分布、更为模糊的界线、比较低的对比度以及减低的特征易变性等，从而进一步降低了图像分割精度。因此，图像分割被认为是计算机视觉领域的核心探索问题。

到目前为止，有许多图像分割方法及其改进形式。由于本文研究的是基于概率图模型图像分割方法，因此，仅对以概率统计作为基础的图像分割处理进行介绍与分析，主要有高斯混合模型(Gaussian mixture model，GMM)和马尔科夫随机场(Markov random field，MRF) 2种分割模型。

传统的高斯混合模型[5]在进行图像分割的过程中，只是利用了像素的灰度，但是并未对各个像素间所对应的空间信息给予充分的关注，所以图像噪声显著地影响了图像分割的最终结果，从而导致分割精度水平低下。针对干扰噪声容易影响常规的高斯混合模型这一难点，文献[6]在图像预处理的基础上，提出了一种基于图像重塑的新型分割方法。该方法通过引入相似性度量因子，利用权值将邻域像素值加权和的结果作为中心像素重塑后的具体像素值，进而分析重塑之后的有关图像。

马尔科夫随机场理论[7]是以统计学相关模型为基础，Geman等[8]在1984年提出并广泛应用于图像处理领域，标注有关的图像像素从而达到图像分割的目的。利用MRF与GRF的等价关系，吴一全等[9]阐明MRF的联合分布是具有特殊形式的Gibbs分布。以马尔科夫随机场理论为基础，许多面向图像分割融合高斯混合模型或者聚类的方法也被相继开发出来。Roula等[10]利用MRF参数对纹理进行了描述，从而提出基于纹理特征的高斯混合模型图像分割技术。同时，科研人员对MRF分割算法做出了进一步的完善，提出了一系列改进的MRF分割模型算法[11]。典型的模型有快速马尔可夫随机场、融合其他分割算法的混合模型以及隐马尔可夫随机场。以图像像素的灰度特征信息为主的学者们[12]将图像的形状特征信息和纹理特征信息引入到马尔科夫随机场中，利用不同的特征提取方法实现对图像特征信息的提取，以各类图像特征信息为基础来改善图像分割效果。

上述分割方法未对相邻像素间所具有的内在关联以及图像空间的信息等因素给予充分的考虑，使得不能以连续的方式来合理地分割某些图像，从而导致所得的结果中形成了数量众多的噪点。本文提出了一种基于有向空间关系高斯混合模型的遥感图像分割算法，主要贡献为：1)设计了一个改进高斯混合模型，合并了像素之间的空间信息对高斯混合模型的先验概率和后验概率进行约束，以提高观测数据场对图像理解的敏感性并进行对应关系的评估和更新；2)引入马尔科夫随机场并和高斯混合模型相结合，通过能量函数中灰度信息的分量控制，解决传统期望极大算法在M步骤无法最大化优化求解缺陷；3)定义的空间约束能够确保图像在进行空间更新时算法结构的稳定，通过交替进行评估像素与类别之间的对应关系和空间约束变换，实现图像的精准分割。与当前流行的3种算法相比，本文所提出的遥感图像分割算法展现出了卓越的分割性能。

1 模型建立

给定获取到的遥感图像X={xi}1≤i≤N，N是像素总数量，xi表示第i个像素的灰度值，同时将图像分割为K个类别标签，第j区域的统计参数用μj、∑j分别表示均值和方差矩阵。模型的参数描述为：

Θ={μj，∑j}1≤j≤K

(1)

图像观测数据对数似然函数是关于图像分割参数的一个函数，描述为：

L(Θ|X)=logP(X；Θ)

(2)

由于缺失数据的存在，即像素xi所属的混合高斯模型分量直接对式(2)进行最大化求解十分困难，因此，引入隐含变量Z={zi=j}1≤j≤K。zi=j表示将像素点xi分配给高斯混合模型的第j个高斯分量。(X，Z)构成了高斯混合模型的完整数据，以给定的图像为观测条件，在隐藏事件空间中将完整数据对数似然函数的数学期望替代式(2)所述的图像对数似然函数，得到式(3)。

ε(Θ|X，Z)=EZ[log(P(X，Z；Θ)]

(3)

给定zi=j即xi属于第j区域条件下，图像像素xi的条件概率分布服从高斯分布，图像像素xi的边缘分布用式(4)表示。

(4)

令πij=P(zi=j)(i=1，2，…，N，j=1，2，…，K)，遥感图像分割模型的完整参数集合用式(5)表示。

Φ={μj，∑j，πij}(i=1，2，…，N，j=1，2，…，K)

(5)

取图像完整数据对数似然期望最大化，利用式(4)～式(5),将式(3)改写为式(6)。

ε(Φ|X，Z)=∑ZP(Z|X，Φ)logP(X，Z；Φ)

(6)

2 遥感图像分割算法

2.1 遥感图像像素的后验概率

根据贝叶斯定理，计算给定图像像素xi条件下zi=j的后验概率αij=P(zi=j|xi)：

(7)

2.2 遥感图像分割目标函数建模

将马尔科夫随机场模型的图像空间信息以先验概率[13]的方式引入到高斯混合模型，将式(7)代入式(6)并取负对数，得到遥感图像分割的条件期望似然函数，用式(8)表示。

L(，

(8)

式中：β为马尔科夫随机场的温度系数。

2.3 遥感图像分割模型参数更新

根据最大后验概率理论判断图像中每个像素的分类标签，从而得到分割结果。对式(8)目标函数求偏导，∂φ/∂uj=0，∀j∈[1…K]，得到式(9)。

(9)

令∂φ/∂∑j=0，∀j∈[1…K]可以实现对∑j的估计，得到式(10)。

(10)

忽略式(8)中不依靠先验的常数项,并利用拉格朗日乘数法，目标函数变为：

(11)

令偏导函数等于0，得到：

(12)

(13)

2.4 算法步骤描述

根据图像分割的标签类别数量，基于K均值算法选择一个计算出的GMM参数的初始值，通过交替进行评估像素与类别之间的对应关系和空间约束变换实现图像的精准分割。具体步骤如下。

1)利用K均值算法进行参数初始化μj和∑j。

2)E步骤。用当前的uj和∑j从式(7)估计αij的后验概率。

3)M步骤。首先利用当前新的αij，从式(9)估计新的均值向量μj；其次，利用当前新的αij，从式(10)估计新的方差∑j。

4)收敛。算法达到最大迭代次数或者小于给定阈值。

3 实验结果与分析

实验样本图像来自在遥感图像场景分类数据集NWPU-RESISC45[14]，样本为bridge_321，像素大小为256像素×256像素。本次实验选择的操作环境为：Intel(R)Core(TM) i5 7 200 CPU@2.50 GHz处理器、Windows 10 64位操作系统，以MATLAB R2010b为工具开展算法验证以及相关性能的测试活动。

实验步骤：1)测试本文所提出遥感图像分割算法的分割效果及收敛性；2)测试温度系数对遥感图像分割结果的影响；3)与其他分割算法的性能对比分析。算法参数初始值由K均值方法获取，分割类别数量K=3，温度系数β取值范围为[0.5，8]。

算法在下面的条件之一将停止：1)连续2次分割结果的改变比率不超过0.001；2)迭代次数超过50。

3.1 样本分割性能测试实验

1) 算法收敛性实验。本节实验主要验证本文算法的分割效果和算法的收敛性，温度系数β设置为1，图1所示为样本图像的分割结果。图1(a)为原始遥感样本图像；图1(b)～图1(d)分别为不同迭代次数下的分割效果，迭代次数依次为2、5和50。从遥感图像的分割过程来分析，在迭代开始时，图像中的孤立像素不仅数量较多，同时分布也十分密集，部分背景区域容易被划分为目标区域，而且不同目标区域之间处于连贯状态，不满足原始影像的要求。随着迭代次数的增加，遥感样本图像线条复杂细节区域的分割边缘细节更为精确和完美，图像余留的噪声点逐渐减少，同时较小的区域能够被良好分割，尽管仍然存在少量的错分情况，但是由于对数函数减弱了权重造成的影响，所以能够较好地划分所有像素的能量。

图1 分割结果

图2显示本文的条件期望似然函数最大化过程中的量化值。通过连续5次迭代操作，实现了快速收敛的目的，所以本文方法可以直接通过EM算法来达到优化参数的目的，与其他方法相比，具有速度快、容易操作、效率高等优势。

图2 收敛过程

2) 温度系数对分割影响实验。本节实验主要验证不同温度系数因子对样本图像分割效果的影响，实验结果如图3所示。图3(a)～图3(d)分别为温度系数β为0.5、2、4、8时的分割结果。通过分析，如果选择β值足够小，能够实现高精度的分割，同时目标轮廓与真实轮廓之间也更加接近。然而分割结果图像中会存在较多的噪声点，无法准确地分割较小的区域且较小区域的分割结果呈离散状，此时该方法鲁棒性很弱，易于误分类。如果所选择的β值足够大，图像中的噪声点大量减少，但是，分割的细节会丢失(例如左上角的桥梁)，较小的区域容易连通(例如河道中间的桥梁)。图4显示了不同温度系数下本文所提出的遥感图像分割算法对测试遥感样本图像分割结果的误分率曲线。分割误分率曲线显示在β为4的时，遥感图像正确分割性最高。

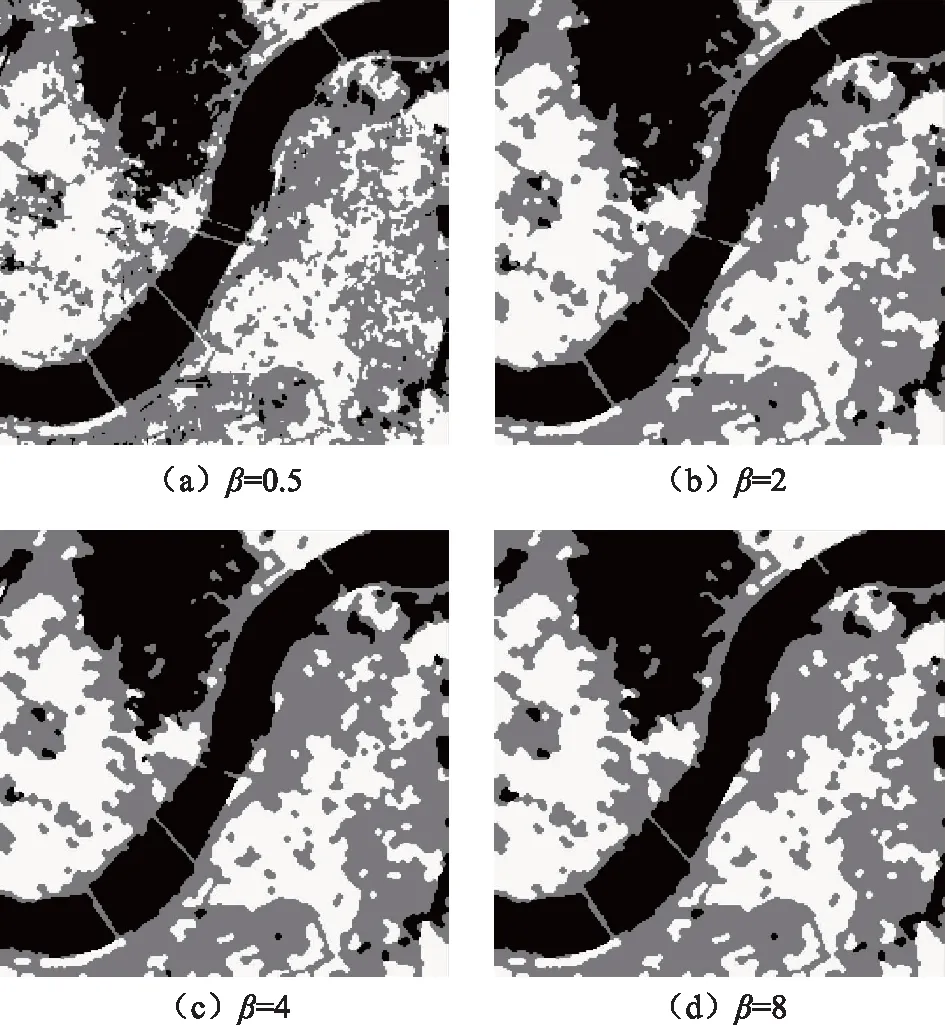
图3 不同温度系数β下分割效果

图4 温度系数β对误分率影响曲线

3.2 遥感图像的不同分割算法对比分析实验

本节对深度学习[15]、GMM以及MRF传统分割算法进行了定性和定量对比分析，以验证本文算法的优势。实验参数设置为：类别区域数为3，β=4，并且选用Jaccard相似度RJ及分类正确率RCCR作为性能衡量指标[16]，RJ和RCCR的取值范围为0到1，数值越大说明算法的分割效果越佳。

图5显示不同算法的遥感图像分割结果。图5(a1)～图5(a4)分别为传统GMM算法、深度学习算法、MRF算法及本文算法的遥感图像分割结果，图5(b1)～图5(b4)为图5(a1)～图5(a4)中红色方框区域放大2倍显示结果。图5说明，参与对比的3种分割算法尽管能够实现分割目标区域的目的，然而分割区域存在着部分噪声以及无效区域，尤其是类之间的边界难以检测，所以传统分割算法会受到噪声影响，导致分割存在较为严重的错误。图5(a1)GMM算法的分割效果较差，图像中的孤立像素不仅数量较多，且分布十分密集，部分背景区域容易被划分为目标区域，而且不同目标区域之间处于连贯的状态，不满足原始影像的要求；图5(b1)中河道内出现了大量错分点，并且河岸的边界轮廓产生阶梯和毛刺干扰现象；图5(b2)为深度学习的分割结果，由于缺少大量训练样本，虽然分割效果较好，但是桥梁出现不完整的过分割显现；图5(b3)的河道内出现错分点且背景出现较多的干扰；图5(b4)为本文所提出分割算法的图像分割结果，能够实现精准分割，同时受噪声影响较小，与其他算法相比，分割效果最佳。

表1是不同分割算法的性能评价参数。性能评价结果表明：1)在深度学习算法、GMM算法、MRF算法分割结果图像中均存在十分明显的错误分类情况以及大量的噪声点，所以它们的指标参数水平较低，而本文采用的分割方法能够实现更准确的分类，同时对噪音的抑制能力也越强；2)因为本文算法可以通过EM算法方式来优化目标似然函数，其他方法不能够进行先验分布操作，所以本文算法方法具有易操作、效果好的优势。

表1 不同算法定量分析统计结果

4 结束语

本文详细介绍了一种基于马尔科夫随机场的高斯混合模型的遥感图像分割方法。首先，根据图像区域特征，利用像素之间的空间信息对高斯混合模型的先验概率和后验概率进行约束，定义的空间约束能够确保图像在进行空间更新时结构的稳定；其次，根据空间像素区域分类信息，通过能量函数中灰度信息的分量控制，确保图像灰度和空间信息的自适应分配，同时通过邻域相关性定义先验概率的引入，提高分割算法对噪声的鲁棒性；最后，利用K均值方法初始化高斯混合模型参数，通过EM算法准确地完成图像的分割。通过性能测试和比较实验，验证了本文算法的分割性能。