驳船浮沉过程的力学模型研究*
2021-01-20杨晓宁
杨晓宁
(大连职业技术学院交通工程学院,辽宁 大连 116035)
0 引言
随着中国造船业与国际海运行业的发展, 运输船舶以及海上结构物朝着越来越大型、 结构越来越复杂的方向发展,其设计、建造、下水以及营运均面临着极大挑战。大型船舶或者结构物下水, 是使其从陆地移动到水中进而实现其价值的重要环节, 目前应用比较广泛的形式有重力式下水、自漂浮式下水和机械化下水三种,其中利用驳船实现各种结构物下水的方式不受场地、下水区域、船坞能力等诸多因素的影响,适用于各种大小、类型的船舶及海上结构物的下水[1]。 本文从力学角度出发,对驳船浮沉过程进行研究,以保证整个下水作业安全。
1 驳船浮沉过程中性能计算
1.1 驳船浮态、初稳性计算方法

图1 船舶坐标系
如图1 所示建立船体坐标系:选取三个相互垂直的基本平面中线面、中站面和基平面,三个面的交点为坐标原点O; 中线面与基平面交线为X 轴, 并指向船首方向为正; 中站面和基平面交线为Y 轴, 并指向船右舷方向为正;中线面和中站面交线为Z 轴,并指向上为正。 船舶浮态通常用首尾吃水来表示,计算船舶吃水,首先需计算船舶的排水量△:

式中,W0是驳船的空船重量,为固定重量;∑P 是其它重量,为变动重量,与其它船舶相比,驳船沉浮过程中上驳产品的重量以及压载舱的压载水量为主要变量。
理论证明,船舶在小角度纵倾时,纵倾轴过初始水线面漂心的横轴,在排水量一定时,其复原力矩计算方法如下:
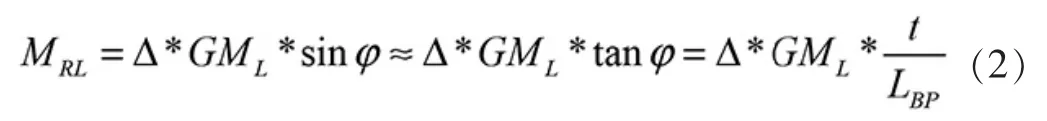
式中, MRL是复原力矩;GML是初稳性高;t 为吃水;LBP是垂线间长。
令t=1cm,则:
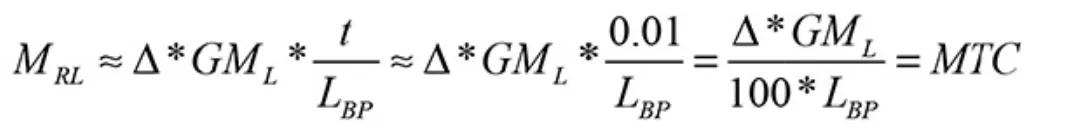
式中:MTC 是船舶为每厘米纵倾力矩,即当船舶吃水差改变1cm 时,船舶本身所具有的纵向复原力矩,可利用船舶的静水力曲线图或静水力参数表得到。
因此,吃水差可按下式计算:

式中:xb是船舶浮心距离船中的距离, 由静水力曲线图中查得;xg是船舶重心距离船中的距离, 可将船舶各项重量重心按以下公式计算得到。
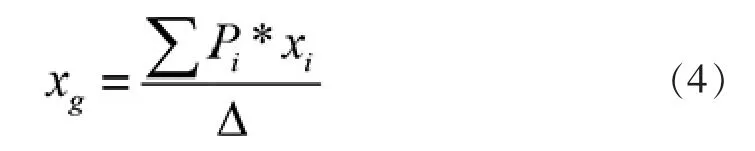
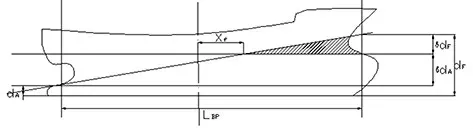
图2 船舶纵倾时吃水示意图
由船舶纵倾吃水示意图2 不难看出:
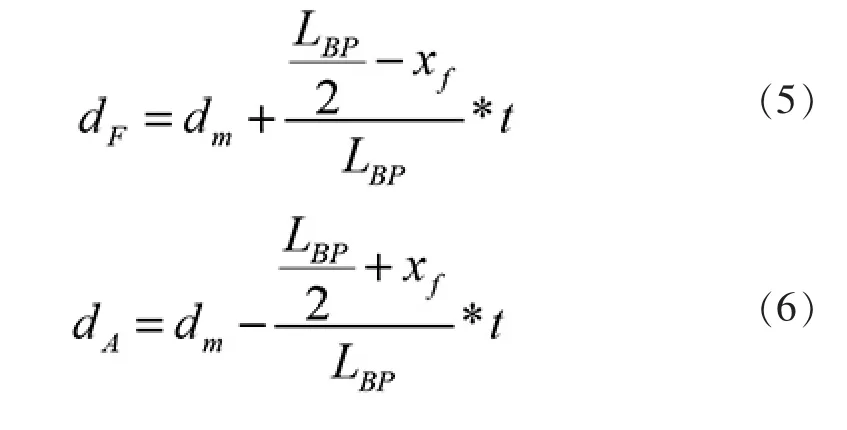
式中:dA为尾吃水;dF为首吃水;dm为当前吃水的平均值,可由静水力曲线查得。
驳船的初稳性计算公式为:
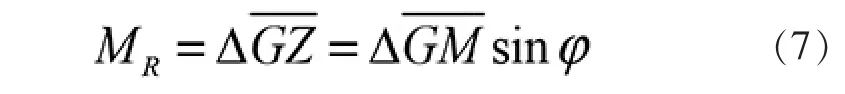
1.2 驳船强度计算
船舶在水上漂浮,重力和浮力大小相等方向相反,整体处于一个平衡的状态,但是,将船舶分成若干个小的区域来看,会发现船舶在任何局部受力中,重力和浮力是不能平衡的,正是由于船舶局部受力不均匀,会导致船舶内部产生剪力和弯矩。 因此船舶强度是影响船舶正常运营的一大要素,如果在船舶营运过程中,忽略强度计算,就会造成船舶结构的破损甚至船体的断裂[2],尤其是驳船沉浮过程中的配载过程,由于压载水量的大幅度调整,载荷的变化对船体强度影响是巨大的。 为了保证配载过程中,驳船结构完整,避免对其船体造成的不良影响,必须实时计算其强度并予以校核。
将驳船的浮力载荷曲线和重力载荷曲线叠加, 得到驳船的外载荷分布:
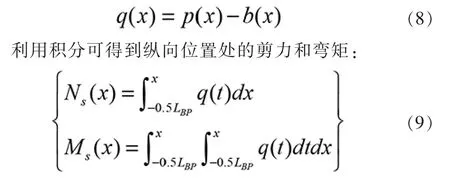
计算完成后, 按照规范要求对强度校核点进行校核即可。
2 驳船沉浮过程中力学模型
利用驳船完成产品下水主要分为两个阶段, 第一阶段为产品从码头上驳到驳船, 第二阶段为驳船在指定海域下沉,完成产品下水。 两个阶段受力情况不同,因此应分阶段进行分析。
2.1 产品上驳阶段
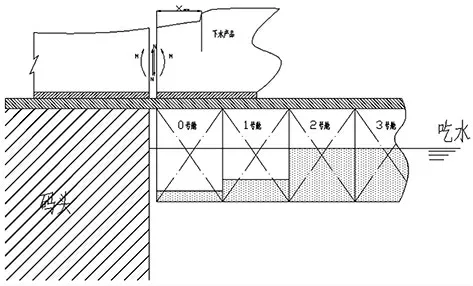
图3 产品上驳示意图
产品上驳过程示意图如图3 所示,将上驳产品和驳船作为两个独立的研究对象,分别考量。 一方面,对上驳产品来说,如果能够保持驳船上表面与码头地面齐平,其上驳过程只是在做平面拖拽运动, 产品内部不会产生由于外力大幅变动带来的剪力和弯矩变化, 整个过程是安全的。 另一方面,对驳船来说,可将产品上驳视作装卸载荷,配载过程只需要依潮水的变化调整压载水量,使得驳船达到平衡条件即可。 综合上述两个方面的分析内容,可以将配载过程简化为调整驳船的压载水量,使驳船处于理想的浮态,同时满足其总纵强度的要求即可[3]。 考虑用优化算法和平衡方程方法对配载过程进行求解。
2.1.1 优化算法
将整个产品上驳过程分解为若干个连续的节点,可知配载的实质是通过实时调节压载舱的压载水量,来平衡每个节点上驳产品的重量,为保证上驳过程的连续性,每个节点配载时间越短越好[4]。 由此可见,可以将配载过程归结为求解约束最优化问题:设置各个舱室的调载水量x 为自变量,调水量的绝对值求和为目标函数,显然,当调水量绝对值求和最小时,配载的时间最短,该方案即为最优[5]。对该优化模型中的限制因素即为力和力矩的平衡, 同时,各个舱室的调载水量必须在舱容范围之内,即不允许大于舱室最大压载水量,同时不小于空舱时残余水量。 利用惩罚函数法或其他优化方法,即可对该优化问题求解[4]。
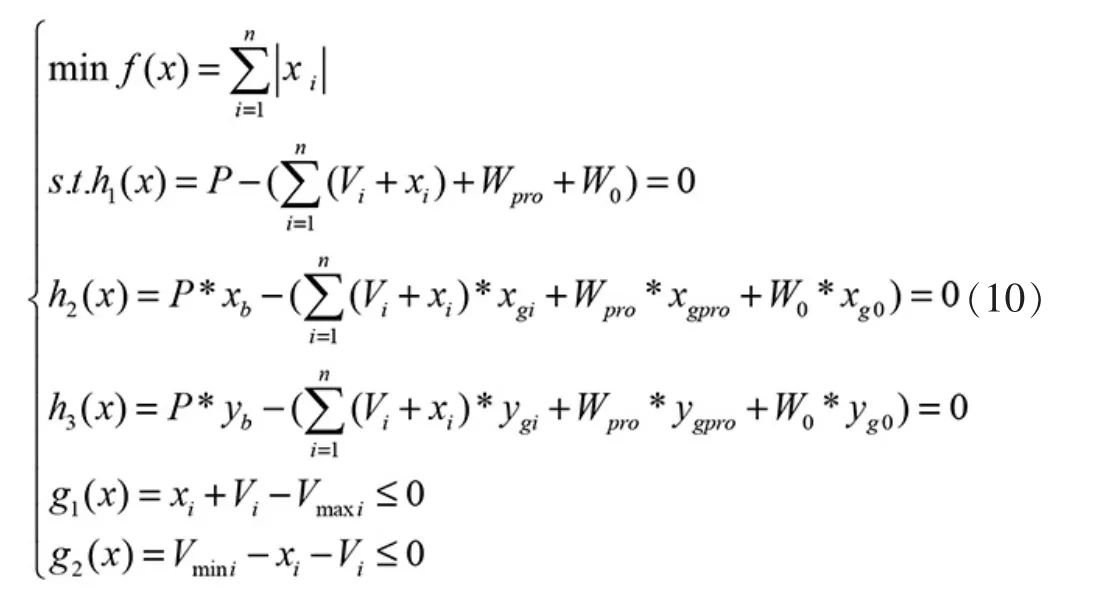
2.1.2 平衡方程法
从配载的实质出发,产品上驳过程,实质是通过调节驳船压载舱中的压载水量, 来抵消产品上驳部分重量,使得驳船达到力和力矩平衡,即:重力和浮力平衡,纵倾力矩和横倾力矩平衡。 依此可建立平衡方程组如下:
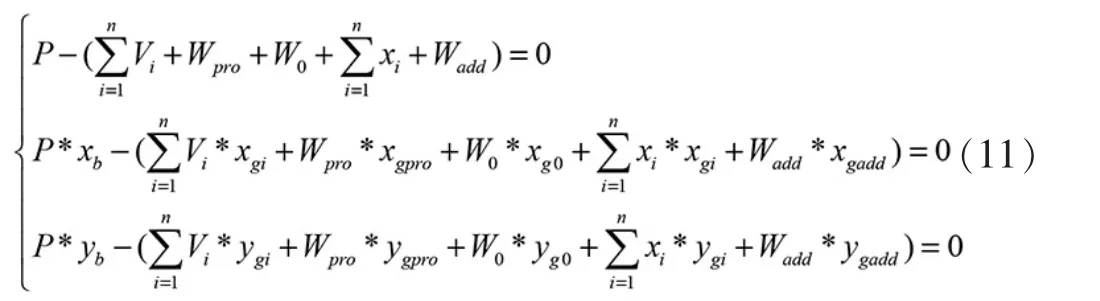
可见,该方程组有三个方程,因此最多只能限制未知数的数量为三,才能求解。 假定在驳船的n 个舱室中只有3 个进行调载,其它舱室水量保持不变,便可以得到个调载方案,依上述方程组很容易便能求得结果。将上述个方案的配载方案进行比较,将每个方案的三个调载水量绝对值求和,最少者为最终方案。
通常来说,上驳产品和驳船均为左右对称结构,调载过程中,只需在驳船横向对称调节压载水量,即可保证在上驳过程中的横向倾斜力矩零。 因此上述问题可进一步简化为两个方程组求解两个未知数。 另外,驳船不同于普通运输船舶,其线形和结构简单,压载舱室具有明显的行列规律,因此,配载问题可以进一步简化为求解m 列中任意两列舱室调载的问题,即在Cn2个方案中选取最优的方案。 将调载的列确定以后, 将该列调水量平均分配到左右对称舱室中即可完成配载。 相对调节三个舱室来说,这种配载方案使得调载水量以及驳船压在舱内水量分布更均匀, 对其结构与强度更为有利。
2.2 产品下水阶段
产品上驳完成之后, 驳船会将产品移运到指定海域后下沉,完成产品下水。 在下沉过程中,为了避免产品滑落水中,造成严重后果,应避免驳船产生较大倾斜,最理想的状态是始终保持驳船处于正浮。 如图4 将下沉过程分两个阶段进行力学分析:第一阶段,吃水1 状态到吃水2 状态,这个过程,产品重量重心未发生任何变化,因此其作为载荷对驳船的受力情况没有影响, 驳船的配载只需通过调节压载水量来抵抗吃水增加引起的浮力变化[5];第二阶段,吃水2 状态到吃水3 状态,由于产品开始进入水中,浸水部分势必会产生浮力,因此产品作用在驳船上的力随浸水深度在实时变化,驳船调载时,需要将这部分内容予以考虑。 最后,当产品吃水达到能够完全支撑自身重力时,驳船便不再受到来自产品的压力。 上述各阶段中,虽然受力在不断变化,但产品相关重力、浮力等计算完全可以按照产品手册迅速得到, 因此配载过程与产品上驳阶段并无实质差异, 而上驳阶段求解方法同样适用于本阶段,不再赘述。
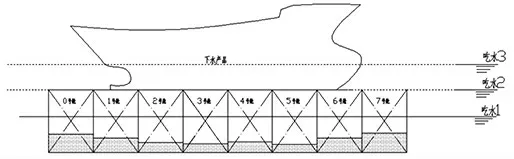
图4 产品下驳示意图
3 计算实例
从工程实际出发, 本文采用求解平衡方程的方法对某驳船上驳阶段中的某一时刻进行计算。 该驳船的数据如下:船长122.4m,船宽59.8m,型深7m,空船重量6 292t,空船中心纵向、横向和垂向坐标分别为-0.375m、0m 和4.944m。 本步调载初始数据:产品已上驳部分重量为666t,重心纵向坐标为-47.686m,浮心纵向坐标为0m,当前时刻潮高331.5cm,结束后潮高333.5cm,本步需上驳产品重量149t。 该船的压载舱布置情况如图5 所示。
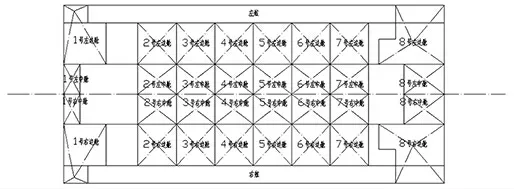
图5 算例驳船舱室布置图
利用计算机程序, 轻松求得本步调载的最优方案为:在2 号舱室左右中舱各排水58t, 在7 号舱室左右边舱各注水41t,配载后驳船的艏左、艏右、艉左、艉右四点吃水均为4.049m, 其横稳性高为45.611m, 纵稳性高为322.418m,最大剪力为6.67E+02tN,最大的弯矩为1.18E+04t*m。 可见, 在本步调载中, 由于潮水的升高需要注水115t,由于产品进入需要排水149t,二者求和,恰好等于四个调载舱室共排水34t,同时船舶个性性能指标均满足规范要求,由此,证明本方法安全可靠。
4 结语
本文从配载的实质出发,提出两种解决驳船在沉浮过程中的配载方法。 计算结果证明方法具有实际的可操作性,并满足工程作业要求。 另外,可将该模型进行适当处理,将其推广到其它运输船舶的调载作业中去,具有较高的实用价值。
