自校正自适应控制系统的设计与研究*

蒋兵兵， 李 玲

（湖南铁路科技职业技术学院，湖南 株洲 412000）

0 引言

随着工业自动化的日益发展， 控制系统的复杂性越来越高，对于一些具有非线性、不确定性、强耦合的系统采用常规控制已不能满足控制要求， 于是自适应控制的概念出现[1-2]。 它的研究对象为具有不确定性的系统，通过及时更正控制器的特性以适应被控对象的参数变化和动态扰动，使整个控制系统始终获得满意的性能。

1 自校正控制的基本思想

自校正控制也称为参数（估计）自适应控制。 它的基本思想为[3]：在掌握结构的基础上，将模型参考估计与控制设计结合起来，通过对模型参数的辨识，确定与其有关的控制器参数，或者直接估计控制器参数，并由控制器算出控制量。

自校正控制的结构框图如图1 所示， 由参数估计器、控制器设计、控制器和被控对象四部分组成。 主要工作集中在参数估计器、控制器设计上。

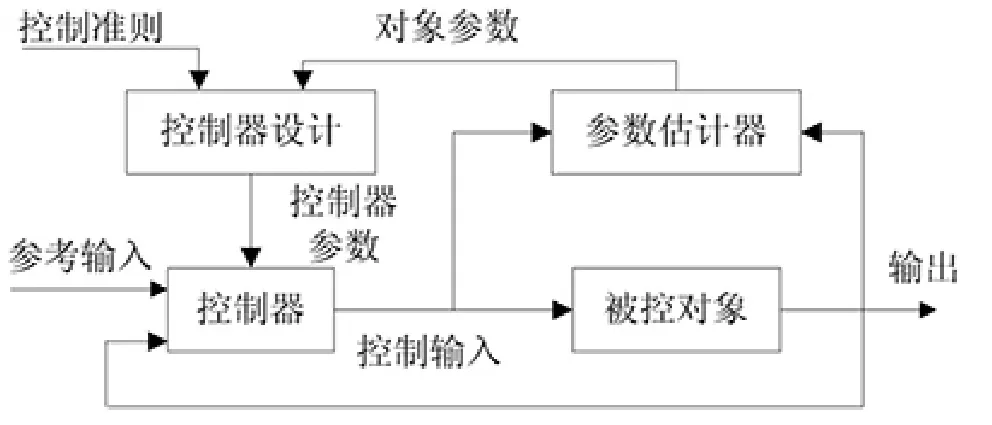
图1 自校正控制系统典型结构方框图

本文选用间接自校正控制系统进行设计与研究，拟采用递推最小二乘法对参数估计器进行参数估计， 用极点配置法来完成控制器设计， 从而完成自校正控制系统的设计。

2 带有遗忘因子的最小二乘法的参数估计器

最小二乘法（Least Square Method） 具有原理简单明了、算法简便快捷、约束较快、易于理解掌握的特点，所以它被广泛应用在参数估计之中。 递推最小二乘法的估算公式为：

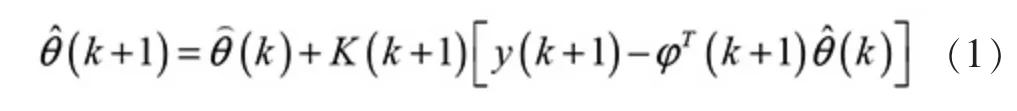
递推最小二乘法往往有一个缺陷：会时不时出现“数据饱和”的问题。 随着k 的逐渐增大，K（k+1）与p（k+1）就会变得越来越小，式（1）中的修正能力变弱。 这就会导致出现以下情况：参数估计值很难接近真实的数值；当参数真值时不时发生变化的时候，最小二乘法就无法跟踪到这种变化，从而导致实时参数辨识失败。 因此可以采用带有遗忘因子的递推最小二乘法。

取性能指标：

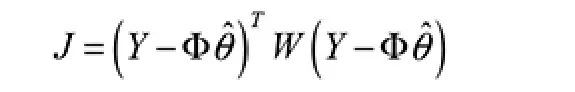
式中：W 为加权对角阵。

根据递推最小二乘的推导思路，可以推导出具有遗忘因子的递推最小二乘估计公式：

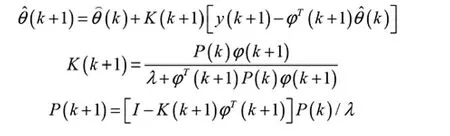
3 具有自校正自适应功能的控制系统设计

3.1 极点配置设计

极点配置（Pole Placement）设计在控制系统设计中是一种经常用到的设计方法， 它具有能适应逆不稳定系统和开环不稳定系统的情况， 并且还具有设计方法直截了当、动态性能良好、系统稳定的特点。

假如设定已知的被控对象或过程用下列方程来进行描述：

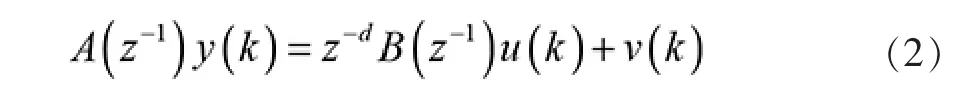
式中：y(k)、u(k)和v(k)分别为系统的输出、控制和干扰，d 为纯干扰。

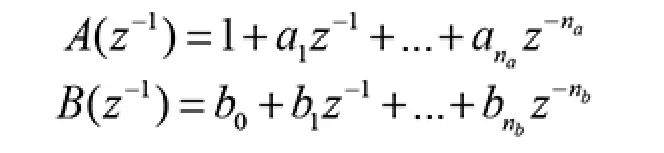
设计控制器为：

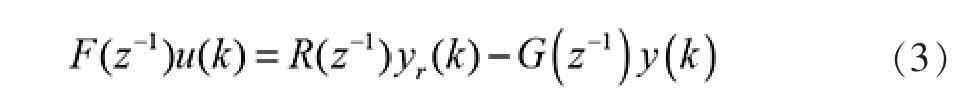
这里F（z-1）、R（z-1）和G（z-1）为待定多项式。

该系统的输出表达式为：

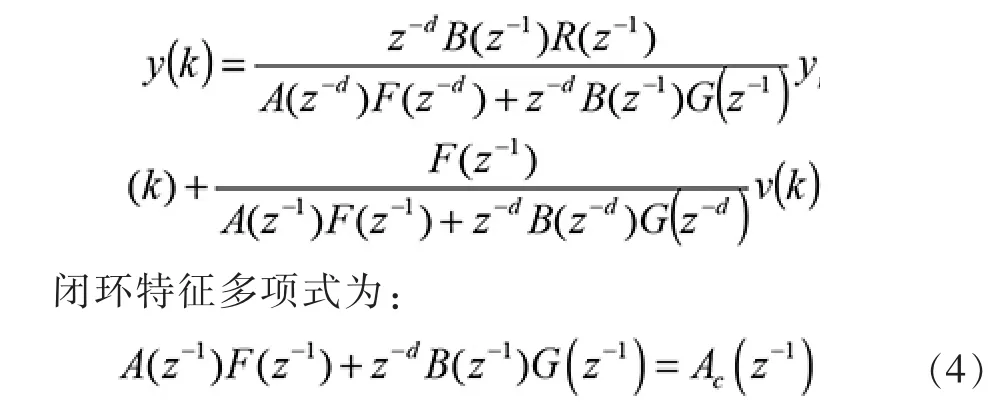
式（4）常常称之为Diophantine 方程式。

设定期望得到的输入/输出表达式为（不考虑干扰因素或者环节）：

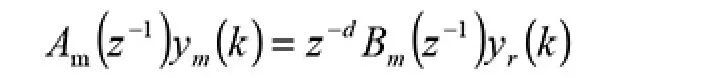
为了简便明了， 将以上所有式中括号内出现的z-1省去，例如A（z-1）简化为A。

然后在输出环节中， 让关于参考模型输入的传递函数与期望得到的传递函数相等，即

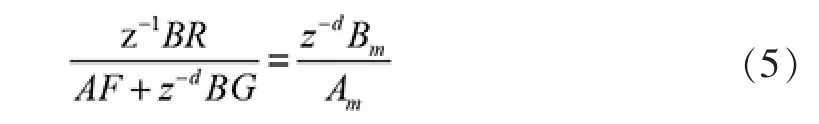
已知：过程多项式A、Z-dB；

性能要求：期望的传递函数分母多项式Am；

相容条件：

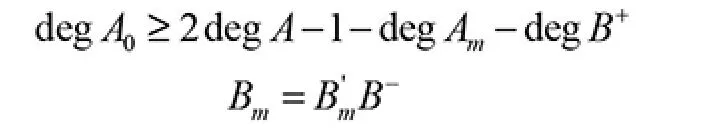
1） 对多项式B 进行因式分解：B=B-B+；

2） 确定了F1、G 和A0的阶次（最大限度的低），并且A0的系数是由不低于Am 响应速度来确定的；

3） 根据Diophantine 方程式的简化形式求出F1和G；

4） 确定F 和R，算出控制量。

3.2 间接自校正控制方法

很多情况下，过程参数未知或时变，就要采用参数估计的方法来进行设计。 首先按分离性原理对控制器的极点配置进行设计，接下来的任务就是来设计估计器。 通常采用递推最小二乘。 将参数估计的结果用于求控制器的参数F（z-1）、R（z-1）和G（z-1）的系数，然后计算控制量，也称为间接自校正控制方法[4]。

设定被控对象或者过程模型公式如式（2）所示，则

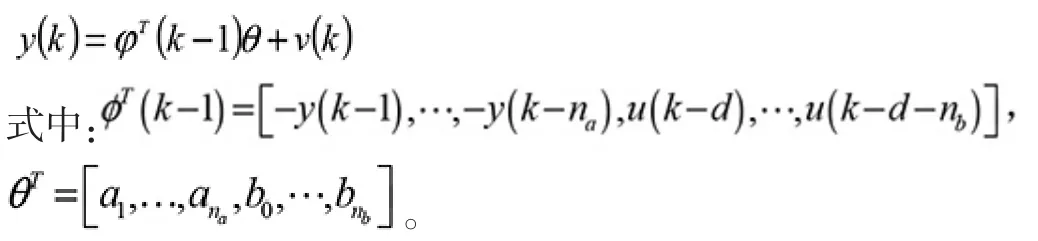
采用具有遗忘因子(λ)的递推最小二乘法，其参数估计公式为：

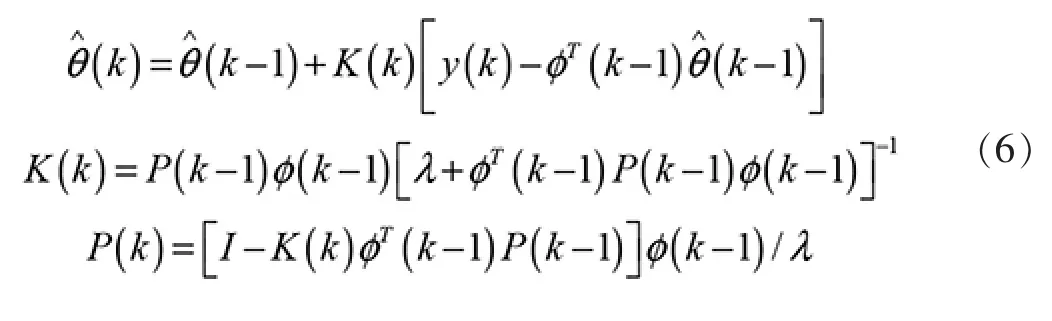
用具有遗忘因子递推最小二乘法和极点配置法的间接自校正控制算法流程图如图2 所示。

图2 控制算法与信号流程图

以某一过程的脉冲传递函数和期望传递函数为例

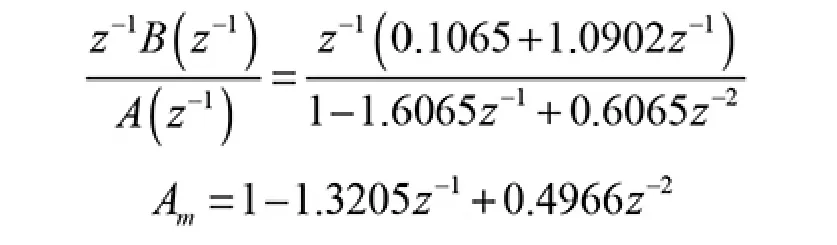
假设上述过程具体参数未知，用极点配置法设计间接自校正控制系统，采用方波作为参考输入，幅值为1。 仿真条件为零点不被对消的情况，取初值。

3.3 基于PID 结构的间接自校正控制

PID （Proportional Integral and Differential Controllers）控制器的离散全量方程式为：

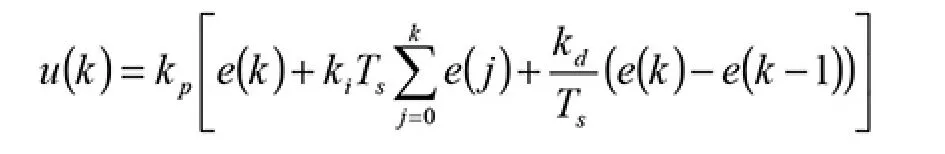
式中：kp为比例增益；积分时间常数为ki；微分时间常数为kd；采样周期为Ts。

离散增量公式为：

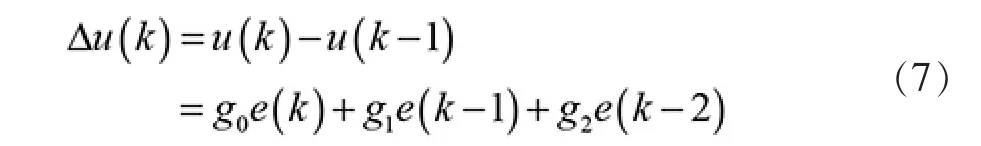
由以上公式可以得出结论：PID 中的参数kp、ki和kd已经被新的控制器中的参数go、g1和g2所替代。 由此对式（7）进行Z 变换，可以得到离散量脉冲传递函数为：

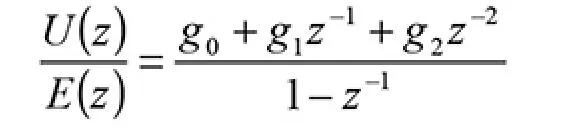
由此可以推导出以下公式：

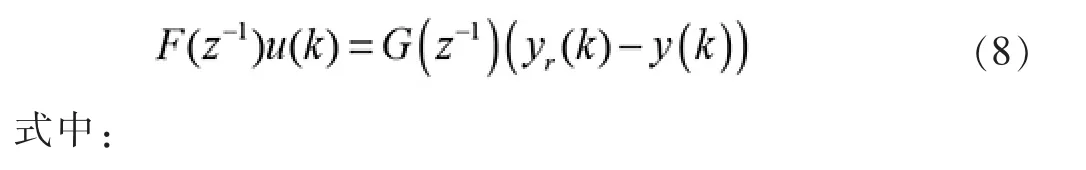
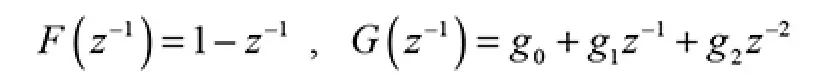
基于PID 的间接自校正控制算法为：

已知：na、nb和d；给定：Am（z-1）；

1） 用带有遗忘因子递推最小二乘法估计对象或过程参数；

2） 由diophantain 方程式求gi（i=0，1，2）；

3） 由式（8）求u（k）；

4） 当k=k+1，又会返回步骤（1）。

尽管基于PID 的间接自校正控制系统在本质上仍然属于极点配置间接自校正控制方法， 但是在待计算的控制器参数仅有3 个，计算的工作量小。

举例分析：某一过程的脉冲传递函数和期望传递函数

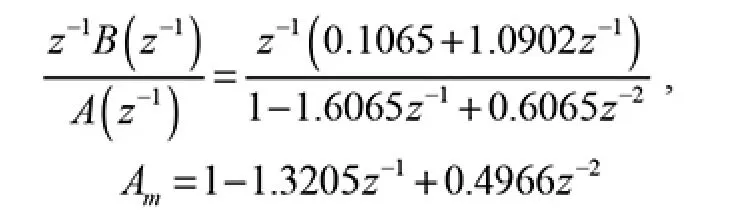
假设上述过程参数未知， 用基于PID 结构的间接自校正控制算法设计系统。 通过MATLAB 仿真[5]，仿真的结果如图3、图4 所示。

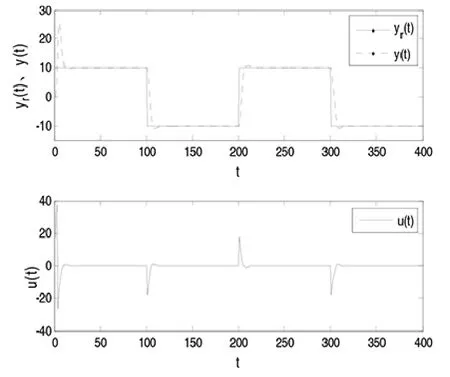
图3 系统输出波形、控制波形

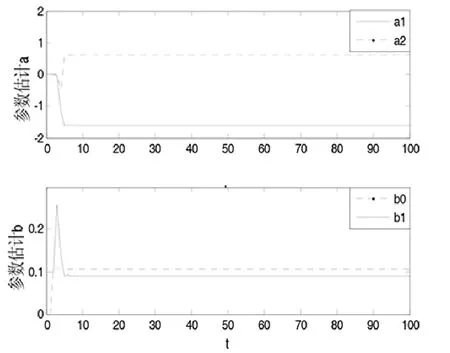
图4 过程参数的估计波形

仿真结果表明系统有很好的稳定性和快速性，系统的输出跟随系统的输入，实现了过程参数的实时估计。 因为该算法的控制器的待求参数只有3 个，计算量小。

4 结论

通过上面理论分析与MATLAB 仿真可以看出， 一种基于PID 的间接自校正自适应控制系统具有较好和可行的控制性能。 本文仅从系统内部本身去分析，从控制系统特征方程的根入手，对自校正自适应控制系统的稳定是有益处的。