基于热力学原理的炉温曲线调控模型
2021-01-20王明泉周心如李博文
王明泉 周心如 李博文
(1、南京信息工程大学数学与统计学院,江苏 南京210044 2、南京信息工程大学大气科学学院,江苏 南京210044 3、南京信息工程大学计算机与软件学院,江苏 南京210044)
1 问题重述
1.1 问题背景
回流焊过程是集成电路板等电子产品生产制造中重要的工艺环节之一,它是通过回焊炉加热从而达到自动焊接电子元件。此过程对回焊炉的各部分温度保持工艺要求极高,可以说焊接质量将直接影响到高精度电子产品的可靠度。目前,这方面工艺的关键即设定回焊炉的炉温曲线大多通过实验测试来进行调控的。
从回焊炉截面角度进行观察,其内部设置分为4 个功能区,包括预热区、恒温区、回流区和冷却区。传送带匀速将电路板送入回焊炉内进行加热焊接。回焊炉也可以分为11 个长度为30.5cm 的小温区,相邻小温区间隔5cm,在加热区外有炉前、炉后两长度为25cm 的区域。生产车间温度保持250C 不变,回焊炉内空气温度也会在短时间内达到稳定,以保证正常的焊接过程。
1.2 需解决的问题
通过建立合适的数学模型,在设定的各温区温度和传送带速度确定下,给出焊接区域中心的温度变化情况,并列出具体小温区的焊接区域中心温度。
2 问题分析
在已知各温区温度设定值的条件下,要求相应焊接区域中心的温度变化情况。考虑到几个温区的相互影响、相互关联,以及传送带运送电子板匀速过炉经过温度不同的大温区过程可看作是炉内空气与集成电子板焊接区域的热传导过程,可以以此建立热传导偏微分方程解释该过程焊接区域中心温度变化情况。依据题中给出某次实验的小温区设定温度及附件中在该条件下的焊接区域中心温度随时间变化数据,可以求出传送带经过各小温区的时间及位置。通过分析得出此类情况为第三类边界条件,基于傅里叶热传导方程和牛顿冷却定律建立不同外界温度下的热传导模型。未知参数可以通过反演求得,针对问题中题设数据求解电子板的焊接中心的温度分布曲线,则需要应用已经建立的热力学模型对电路板焊接区域中心的温度进行正向解。
3 模型假设
3.1 炉内充满同种空气(如氮气)且分布均匀。
3.2 回焊炉内若干个小温区规格完全相同,焊接过程中不存在设备损坏问题。
3.3 焊接区域的质量可靠,即不存在焊接区域出现故障。
4 问题模型的建立与求解
4.1 模型的建立
(1)建立坐标系各小温区可根据温度划分为7 各大区域,在这些区域中,焊接区域的外界环境定,以回焊炉前端为坐标原点,沿传送带运送方向为y 轴建立一维坐标系Oy。
小温区对焊接区域的传热可看作是一维的热传导,以电路板焊接区域的上表面为坐标原点,沿焊接中心建立一维的坐标系Ox。
(2)建立方程
热量的传递通过温度反映,焊接区域由表面到中心的温度变化过程与焊接区域经过小温区对应时间相关,以小温区1-5为例,在小温区1-5 中温度恒定1750C,如图2 将焊接区域由上往下分成不同的层面,每个层面取面积微元dS,各层之间间隔为 Δx ,温度传导由x 往 x +Δx方向,温度变化由u(x,t)变为u(x,t+dt),由傅里叶热传导定律可得:
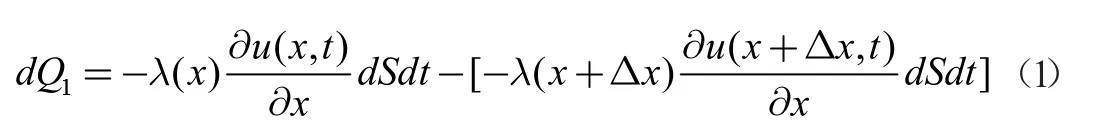
由热量公式 Q = cmΔ u可得:

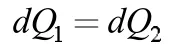

其中L 为焊接区域厚度为0.15mm,t1为传送带经过小温区1-5 的时间。
关于传送带过炉时间t 的描述,考虑如图1 建立时间轴。
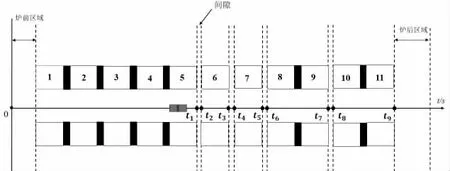
图1 传送带过炉时间轴

上式即为传热二维偏微分方程。
(3)初始条件及边界条件
由于外界环境即小温区1-5 的温度设置为1750C,且电路板过炉的温度最初是250C。所以初始条件为:

利用牛顿冷却定律来确定边界条件,流过第一层上边界的热流等于外部空气和焊接区域之间交换的热流,除第一层外的第i 层与与第i+1 层的热量交换则通过热传导,应用第三类边界条件有:

综上所述,可以得到1-5 小温区段的非稳态热传导模型如下:
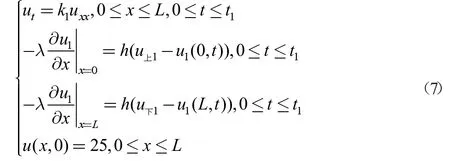
因此小温区1-5、6、7、8-9、10-11 的热传导模型如下(其中i=1,2,3,4,5):
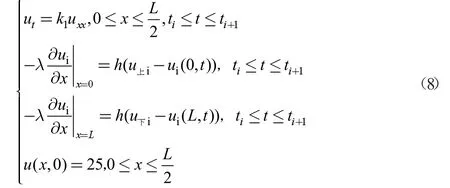
(4)不同大温区的间隙的模型
此前建系时对小温区人为分段,应用温度相同的准则划分,相同温度的小温区合并温度段,不同温度的温区之间留有间隙,这些间隙分别存在小温区5 与小温区6 之间、小温区6 与小温区7 之间、小温区7 与小温区8 之间、小温区9 与小温区10之间,共四个间隙,每个间隙长5cm。这些间隙中热传导模型与上述大温区段有所区别。

图2 间隙表示图
以间隙1(小温区5 与小温区6 之间间隙)为例,间隙左边为小温区5 的温度1750C,间隙右边为小温区6 的温度1950C,间隙两侧温度不一,为更好的过渡该区域温度,采用线性方程对间隙温度进行描述,间隙中,用一次多项式插值:

其中, y =vt,已知焊接区域过间隙的时间t1,t2,代入方程:

可以解得参数a,b 的值,确定线性方程:
u (t )= avt +b 。
另外,大温区 I1, I2, I3, I4,I5;小间隙 D1, D2, D3, D4,D5。间隙温度确定后,其区域所带有的热量传递给焊接区域,可以代入方程求解:
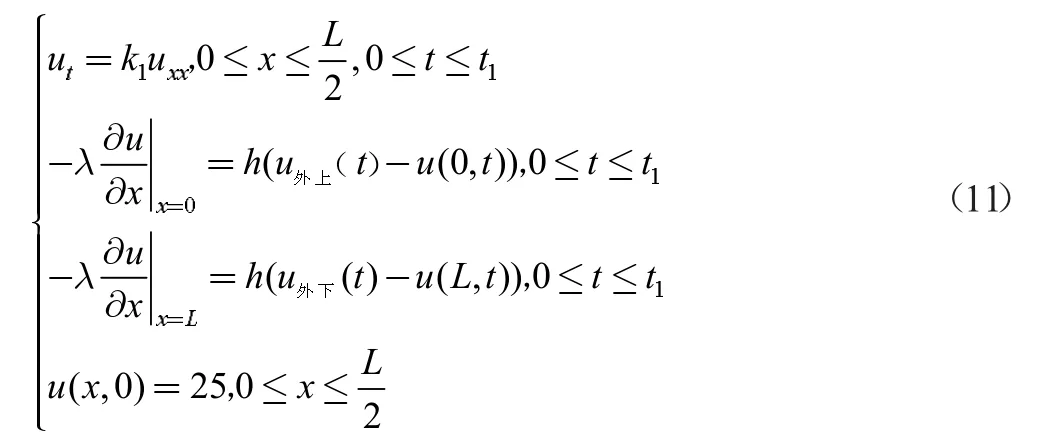
此模型即为回焊炉对焊接区域的热传导模型。
4.2 模型的求解
(1)热传导方程的处理
上述建立的模型是一系列偏微分方程组,无法求得它们的解析解。所以此处考虑求得方程的数值解。此处偏微分方程组中控制方程的形式是抛物方程,边界条件是线性的。所以对数值解的求解考虑采用有限差分法。
时间方向作向前差分,步长△t, 空间方向中心差分,步长△x。

其中,M表示传送带过炉最长时间,N 表示电路板焊接区域厚度。
由差分方程组可知
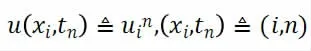


图3 向前差分格式
对微分方程作向前差分格式后,整理得:

上述迭代式表示为差分格式的矩阵:

对上述矩阵以及边界条件求解即可得到离散后的所有时间- 空间节点上对应的温度值。由此即可求得一维热传导方程组的数值解。
(2)参数的计算
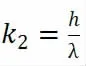
(3)炉温曲线模型的校对
根据附件所给某次实验中炉温曲线的数据,对数据进行可视化处理后,初步观察发现,预热区温度为焊接区域中心温度至1500C;为防止焊接区域熔化,恒温区温度大致稳定在1500C-1700C;回流区的温度会在到达2170C 后继续上升一段时间至温度峰值;温度一旦达到峰值,立即进入冷却区,温度最终降至1000C 左右[2]。将反演得到的参数带入差分方程中,可以得到速度为78cm/min 时的温度情况,与实际值进行对比,得到如图4 所示的炉温曲线对比图。由于理论值温度开始的时间为0s,所以在误差允许的范围内,该模型能够较好地反映原始数据的温度走势,与实际真实数据较为接近,收敛性较好。差分的求解在峰值温度附近出现与实际值较大的波动,原因是传温过程仅存在热传导而不存在热对流。但这在实际情况中是不存在的,横向空气间温差的存在一定会产生对流,也就是说最后的冷却区温度不可能保持在25?C,而模型中将其当做5 的250C处理显然会在最后的冷却阶段产生较大的误差。
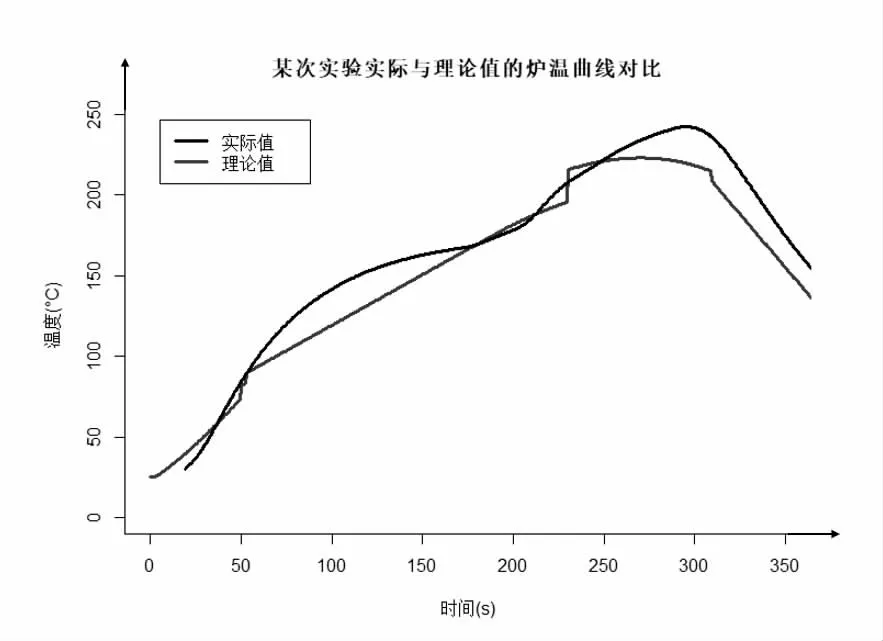
图4 过炉速度70cm/min 炉温曲线实际与理论对比图
4.3 结果分析
将从附件中计算得到的参数值带入差分方程中,根据Fourier 热传导定律并结合电子板在经过各个小温区的初始时刻、温区之间间隔以及回焊炉的边界热量交换过程,采用有限差分法正向求得78cm/min 情况下的炉温曲线。
在问题1 设定的过炉速度以及小温区温度值下,画出的炉温曲线走势基本与实际炉温曲线符合,焊接区域中心基本平缓升温,在达到峰值后冷却。由此得到题目指定焊接区域所在温区位置点的温度(表1)。

表1 小温区3、6、7 中点、8 结束处的焊接区域中心温度结果
根据上述炉温曲线求出每隔0.5 s 焊接区域中心的温度部分结果(表2)。

表2 过炉速度78cm/min 每隔0.5s 焊接区域中心的温度(部分)
5 问题模型的建立与求解
5.1 模型的优点
5.1.1 用线性方式处理间隙温度,更好地模拟回焊炉内工作温区温度变化。
5.1.2 运用热传导模型能够很好地解释回焊炉传热原理,能够从机理分析的角度充分反映各小温区设定温度是如何影响焊接区域中心温度的。
5.2 模型的缺点
5.2.1 忽略回焊炉内空气横向对流和维持一定温度耗损能量,简化热量来源。
5.2.2 在运用有限差分时,遍历步长选择0.01,虽然足够接近真实值,但与真实值之间仍存在差距。在误差分析中,尝试选择不同步长以检验模型准确性,虽然能基本解释步长对模型的影响,但是对于步长求解精度需要进一步分析研究。
5.3 模型的改进
5.3.1 在模型求解过程中对于偏微分方程的处理,选择向前差分格式对传热过程进行描述,一定程度上能够反映其中的机理,但对于精度更高要求的热传导模型,可能存在更好的方式如中间差分法、迭代法能够更加准确地描述这一过程。
5.3.2 在模型的拟合过程中,从拟合结果来看,前半段的拟合较为贴合实际,后半段的拟合的误差较大,这是因为焊接区域在传送带的最后阶段接触到的是空气,存在热量交换,所以要得到更加精确的结果,应该对边界温度作出更高的要求,即考虑空气与焊接区域的热量交换情况。
