基于CFD-DEM模拟物料流在转运点处的流动特性*
2021-01-19石癸鑫幸福堂梅丹黄悦
石癸鑫 幸福堂,2 梅丹,2 黄悦
(1.武汉科技大学资源与环境工程学院 武汉 430081;2.冶金矿产资源高效利用与造块湖北省重点实验室 武汉 430081)
0 引言
在工业生产中,输送带因具有转运方便快捷等特点而被广泛使用。但是在输送带转运点处,物料从高处往下落及落到底层输送带过程中,会有大量颗粒物扩散到周围空气中,这些游离的颗粒物若未经处理不仅会造成空气污染,而且会对工作设备和人员健康带来一系列危害[1-3]。为了解决上述问题,需要在输送带转运点处安装局部密闭式防尘罩清除游离出来的大量颗粒物[4]。在实际生产中,该处的防尘罩大致可分为两种:柜式局部密闭防尘罩和倾斜式局部密闭防尘罩[5],如图1所示。这两种防尘罩虽然可以有效控制粉尘,但是它们的设计并未考虑气固两相流的流动特性,造成物料在输送过程中气固两相流与防尘罩壁面碰撞的角度过大而引起不合理的诱导气流[6-8]。这不仅影响设备的使用寿命,还会增加二次扬尘的产生,而二次扬尘会带来物料的浪费、除尘系统的磨损加大和维护工作更加频繁等问题。因此,基于节约资源、控制生产成本的考量,需要设计一款经济合理、高效的防尘罩。
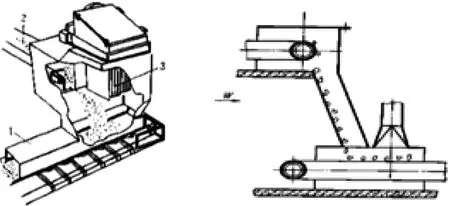
(a)柜式 (b)倾斜式
1 模型选择
对输送带转运点处在设备运行时的流场情况进行研究。在物料颗粒流下落过程中,颗粒和空气是相互作用的[9-11],不仅颗粒会影响空气的运动特性,反之空气也会影响到颗粒的扩散以及运动轨迹。根据查阅相关文献[12-17]和对前人的研究分析,发现CFD-DEM耦合模型在处理气固两相流问题中应用比较广泛,且在技术研究上也比较成熟。
因此,本文在对输送带转运点处流场研究中采用CFD-DEM耦合模型来模拟此处气固两相流运动。该双向耦合模型的实现,需要借助于Fluent软件(CFD)和EDEM软件(DEM),两个软件在模拟计算过程中,需要进行数值的相互交换、传递。耦合流程如图2所示。
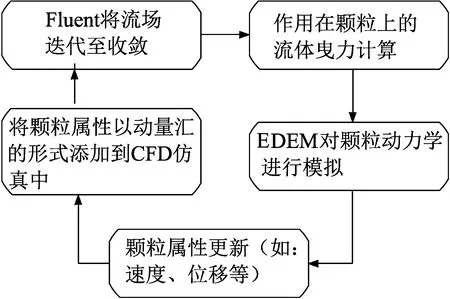
图2 CFD-DEM耦合流程
2 数值模拟
2.1 数学模型
在Euler坐标系下处理连续的流体运动,在Lagrange坐标系下处理离散的颗粒运动。其中,流体运动用Navier-Stokes方程描述,颗粒运动用牛顿第二定律描述,两相间的耦合由牛顿第三定律确定。
2.1.1 气相运动方程
本研究中,物料颗粒的气固两相流属于稠密两相流,假定气相为不可压缩流体,其控制方程包括连续性方程、动量守恒方程及用来闭合的RNGk-ε控制方程组。但在稠密两相流动中,固相的存在对流体运动特性的影响较大,故需要在传统N-S方程中引入空隙率来表征特定计算网格内气相所占体积。
(1)连续性方程
由于连续相为空气,是不可压缩的牛顿流体,密度ρ为常数,可得方程如下:
(1)
(2)动量守恒方程
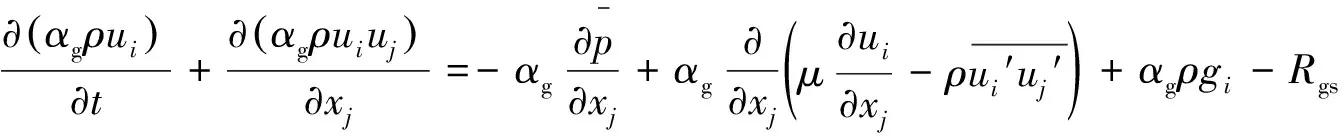
(2)
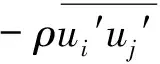
根据Boussinesq假设:
(3)
式中,μt为湍动粘度,Pa·s;k为湍流动能,m2/s2;δij为“Kronecker delta”符号(当i=j时,δij=1;当i≠j时,δij=0)。
(3)湍流动能k方程
(4)
式中,ε为湍流动能耗散率;Gk为湍能体积生成率,kg/(s3·m)。
(5)
式中,△u、△v分别为气、固相的瞬时速度脉动量;vp为固相速度;右边第一项为固相颗粒阻力产生项;第二项为再分布项,代表固体颗粒的运动动能与携带固体颗粒的气体动能的转换关系,计算如下:
(6)
(7)
式中,dp为颗粒粒径;ρp为颗粒密度;τ1为气相的拉格朗日时间尺度;τd为固相颗粒响应时间;CD为颗粒的阻力系数。
(4)湍流动能耗散方程
(8)
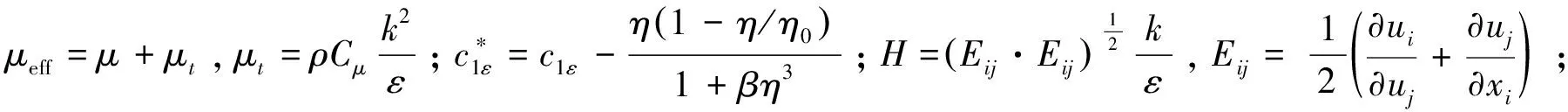
2.1.2 颗粒相控制方程
在颗粒粒径相同的情况下,其他力相对于重力和Basset力来说,数量级微小,而Basset力只在加速运动初期才起重要作用。因此,研究颗粒在空气运动过程中,气流作用于颗粒的曳力对颗粒运动具有决定性作用,只考虑曳力即其他力可以忽略不计。
颗粒在空间中具有平动和转动两种方式,其中运动规律由牛顿第二运动定律描述,即:
(9)
(10)
式中,mi、vi、ωi和Ii分别为标号i的颗粒的质量、线速度、角速度以及转动惯量;k为和当前颗粒相接触的周围颗粒和壁面单元的总数;Fc,ij和Mij分别为当前颗粒i与颗粒j碰撞产生的接触力和力矩;Fd,i为流体作用于当前运动颗粒的曳力。当颗粒和壁面接触时,将壁面视为一个具有无限大直径的静止颗粒,以此来计算两者之间的作用力和力矩。
流体曳力计算如下:
(11)
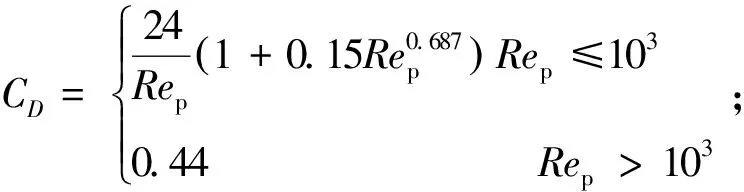
2.2 物理模型
本文对输送带转运点处的物理模型做了简化处理。物理模型计算域为长×宽×高为4.5 m×2.5 m×2.5 m的长方体;底层输送带为长×宽为3 m×0.5 m的矩形;上输送带末端为宽×高为0.5 m×0.5 m的矩形;上输送带两侧设置挡板。输送带的材质为PVC,挡板的材质为钢铁。
模型网格利用ICEM CFD软件,自动生成非结构性网格,Mesh Type为Tetra/Mixed。
2.3 边界条件及模拟参数确定
选取等粒径的氧化铝颗粒作为物料颗粒,输送带均以水平方向1.5 m/s的速度运行,物料颗粒经上输送带自由下落到底层输送带上。周围空气为初始静止,仅受物料颗粒运动影响。然后进行如下前提假设:①气相是不可压缩的;②颗粒的密度大于气相密度;③颗粒为球形颗粒,并具有相同的直径和密度;④计算域为开放式,即与外部空气环境相通。
CFD-DEM耦合的软件设置:在EDEM软件中开启耦合连接开关,然后在Fluent软件中读取已编译好的接口文件,随后在Models中便出现了EDEM-Coupling的连接选项,打开这个选项开始连接。两个软件的参数设置如表1、表2所示,设置完成后,在Fluent软件中点击Calculate按钮进行模拟计算。
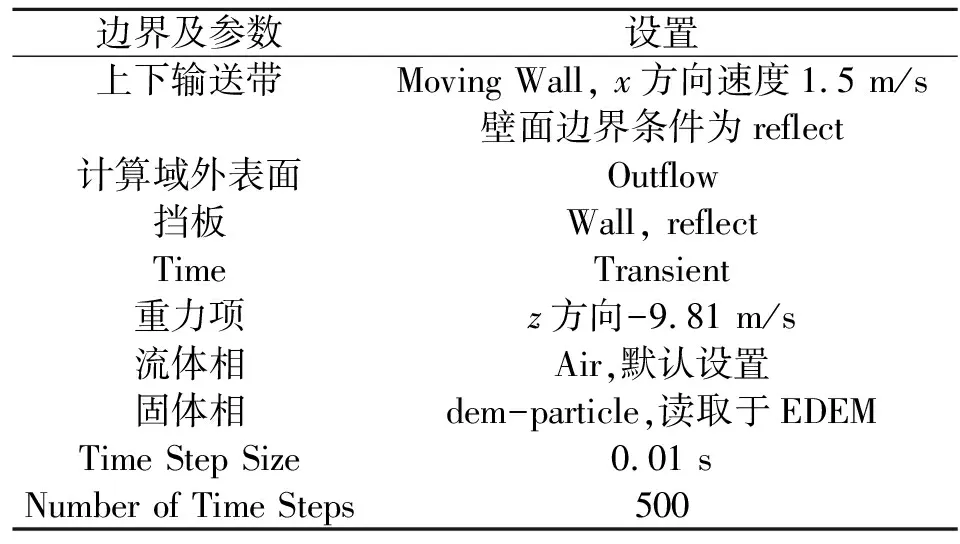
表1 Fluent中边界条件及参数概括

表2 EDEM中材料参数设置
3 结果与讨论
3.1 颗粒运动分析
颗粒流分别在两个模拟软件中的运动轨迹如图3所示。
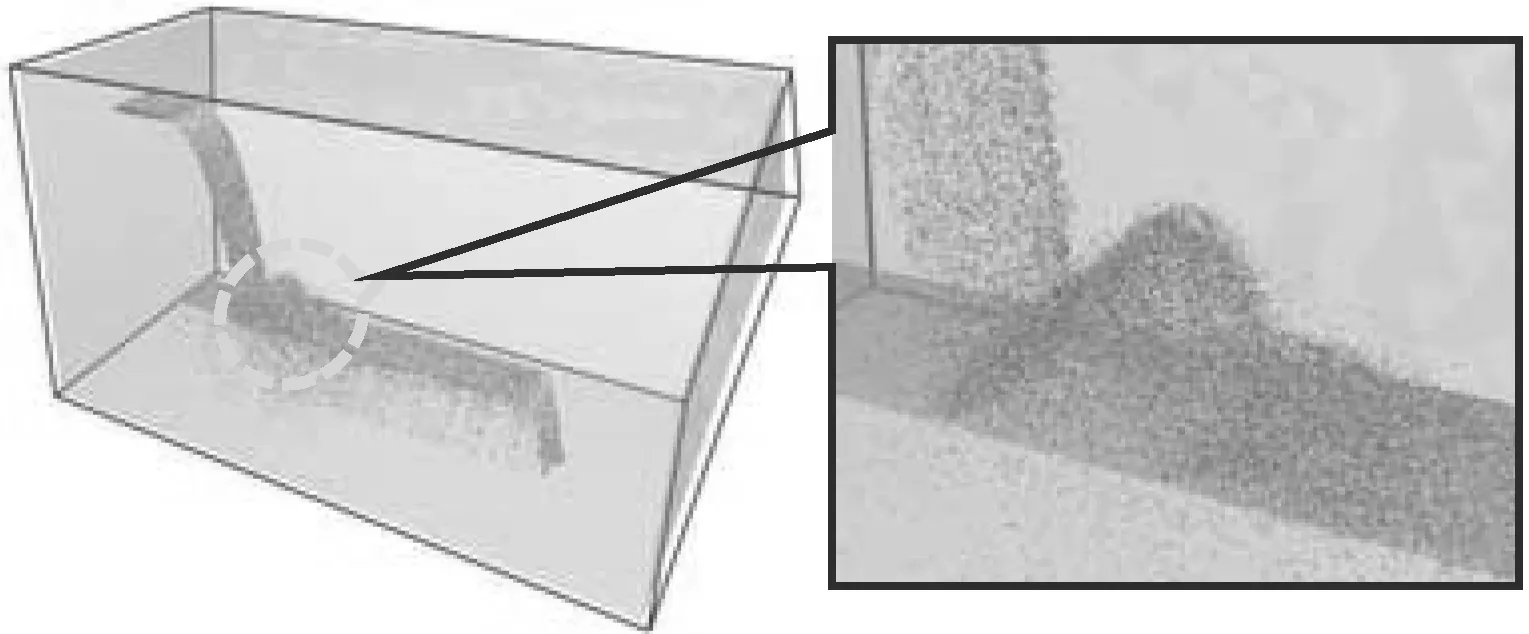
(a)EDEM
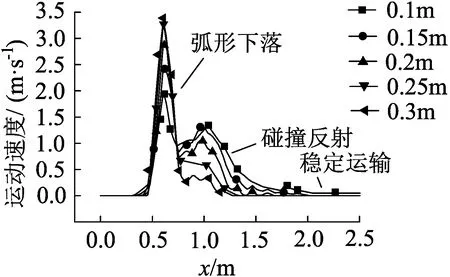
综合图3所显示的颗粒运动情况,物料颗粒在转运点的运动分为3个过程:弧形下落过程、碰撞反射过程和稳定运输过程。
为方便观察物料颗粒在静止空气中的运动规律,将在Y=250 mm的zx平面上且上下带为1.5 m的高度内,选取z方向分别为0.1、0.15、0.2、0.25、0.3、0.4、0.5、0.7、0.9、1.1、1.3 m的11个高度的数据进行分析。其中,碰撞反射过程发生在下输送带部分,颗粒运动复杂且变化较大,故选取的高度较稠密。
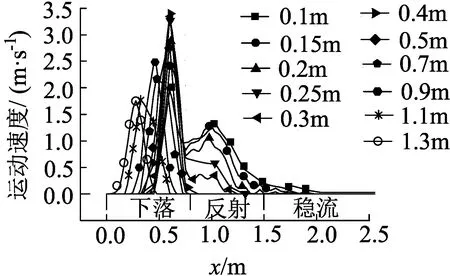
物料颗粒在不同高度的平均运动速度如图4(a)所示。从总体上观察到,有两个速度极大值的出现,第一个速度极大值为颗粒流下落时羽流的核心区域,由于卷吸空气的原因,部分颗粒逐渐向四周扩散,随着扩散直径的增大,速度逐渐减小;第二个速度极大值的出现是由于颗粒流下落到输送带上后,与其发生碰撞反射的缘故,极大值位置为反射后颗粒流的核心区域;图形右端的曲线变化逐渐趋于一致,即颗粒流进入了稳定运输阶段。
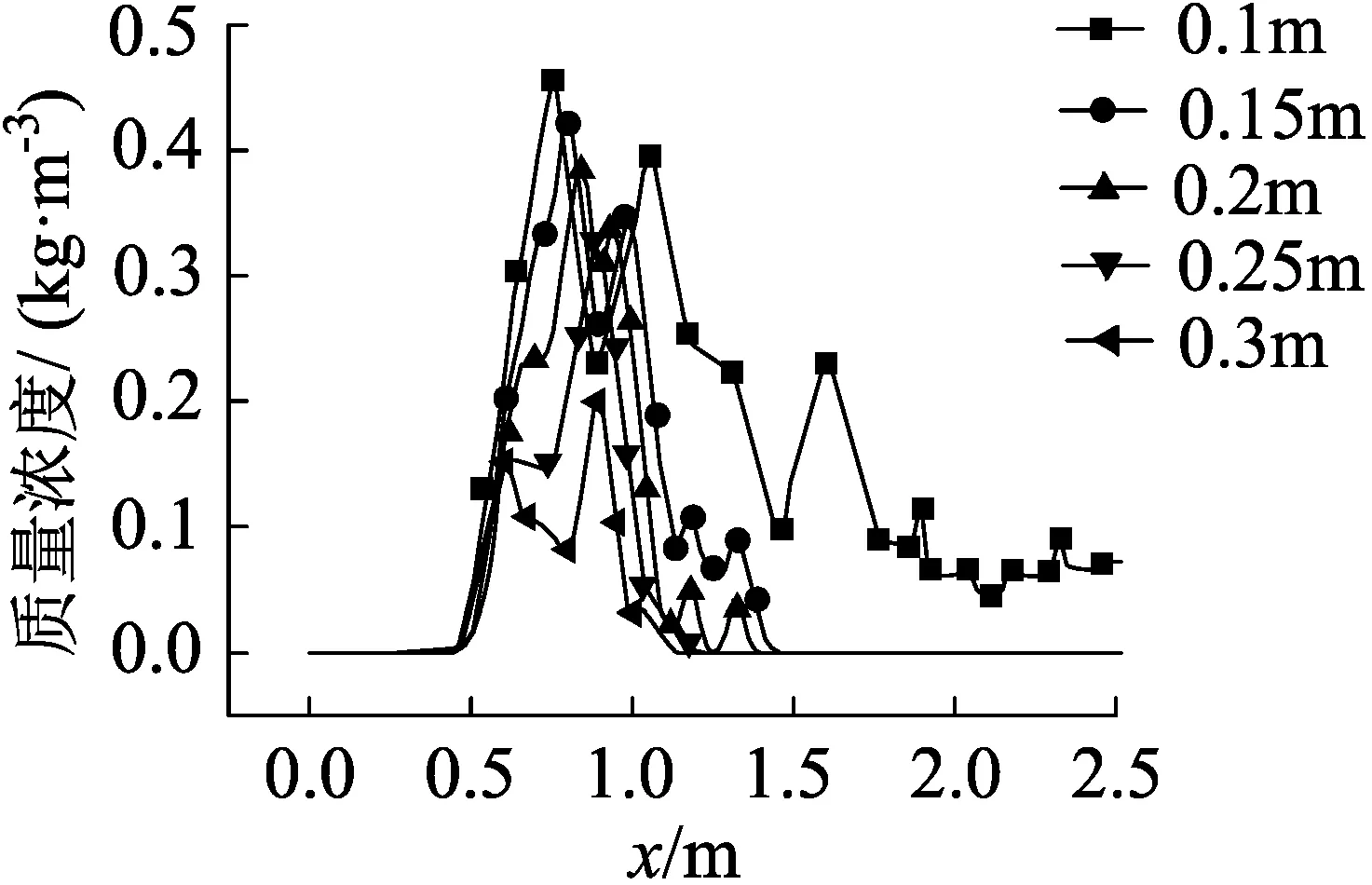
物料颗粒在不同高度的质量浓度大小分布情况如图4(b)所示。从总体上来看,高度高的只出现一个极值,高度低的出现多个极值,且极值的位置随高度的增加而向左移动,与颗粒流运动规律相符,即:刚开始为自由下落阶段,由于存在水平初速度的原因,颗粒流呈弧形下落;当颗粒流下落到底部输送带时,发生壁面碰撞反射现象,颗粒再次被扬起,使底层的颗粒质量浓度增加、范围扩大;最后进入稳定运输阶段,颗粒物质量浓度基本维持稳定。
(a)速度分布
根据颗粒流运动的速度和质量浓度变化规律,将11个不同高度大致可以分为两个部分,如图5和图6所示。图5(a)和图6(a)选取高度为0.1~0.3 m的变化曲线,这部分包含了3个运动阶段;图5(b)和图6(b)选取高度为0.4~1.3 m的变化曲线,这部分只有颗粒流弧形下落阶段。
(a)高度为0.1~0.3 m
结合图5和图6可以看出,颗粒流碰撞反射的最大高度在0.3~0.4 m之间。从x轴约1.5 m以后,颗粒流进入了稳定运输阶段,颗粒流的最大高度在0.1~0.15 m内。从图5(b)颗粒流在自由下落阶段的速度变化规律可以看出,颗粒流在不同高度的扩散半径为该高度曲线上从速度极大值到0值反映在x轴上的长度;颗粒流核心区域在空间上的位置为:X为极大值所对应的x轴值、Y为250 mm、Z为选取曲线的高度z。
(a)高度为0.1~0.3 m
3.2 压力流场分析
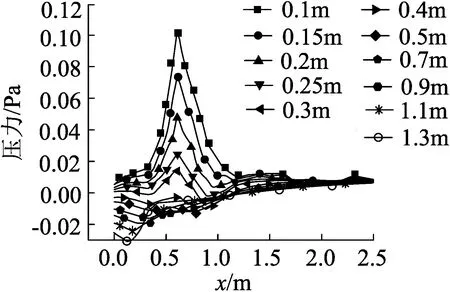
在输送带未运行前,周围空气为静止的、无流动,压力为标准大气压且均匀分布;在输送带开始工作后,由于受到物料颗粒运动的影响,四周空气产生流动现象,流场的压力分布也随之变化。设备运行中压力流场变化曲线如图7所示。
(a)压力分布
由图7观察到,空气流速及压力分布曲线的变化规律,同样可以按照颗粒流运动分析的划分标准,划分为如图8和图9所示的两个部分:图8(a)和图9(a)的高度为0.1~0.3 m,图8(b)和图9(b)的高度为0.4~1.3 m。
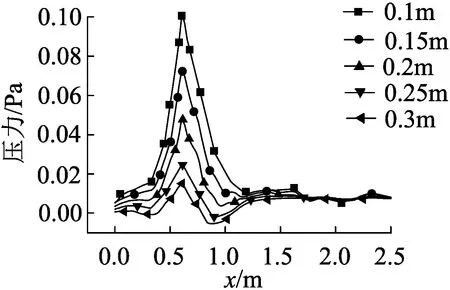
(a)高度为0.1~0.3 m
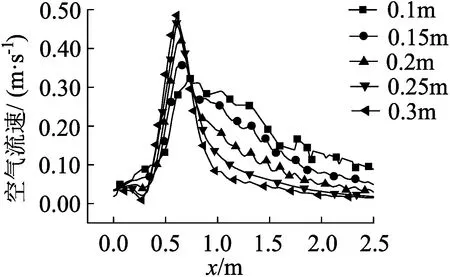
(a)高度为0.1~0.3 m
根据图8(a)和图9(a)所示,颗粒流核心区域的压力值最大,空气流速也最大,这是因为受颗粒流扩散的影响,在同一水平上空气运动方向与颗粒流扩散方向一致,空气的运动动力由颗粒流运动提供,颗粒流在扩散的过程中速度逐渐减小,空气运动速度也随之减小。在图8(b)中,从压力变化曲线上看,压力值在刚开始下落时并未出现极大值,而随着下落的高度增加,极大值的效果逐渐显现。这主要是因为该运动过程处于自由下落阶段且在水平方向具有初速度,所以颗粒流在初始下落时水平方向上的初速度起主要作用;随着下落高度的增加,水平方向上的速度因空气阻力而减小,竖直方向的速度受到重力加速度的影响而增大并逐渐起主要作用。观察图9(b),在下落的过程中,颗粒流核心区域的空气速度随着颗粒流速度在竖直方向上的增加而增大,在同一水平上由核心区域向外扩散过程中空气速度逐渐减小,空气速度曲线的对称性与图9(a)相比较好,这是因为图9(a)的右侧受到带面碰撞反射的影响,空气速度出现增大现象。
3.3 结构改进
通过上述对输送带转运点处的颗粒运动分析和压力流场分析,对分析的结果整理如下:
(1)运输过程分为3个阶段:弧形下落阶段、碰撞反射阶段、稳定运输阶段。
(2)在弧形下落阶段,颗粒流呈弧形下落及向周围扩散,扩散半径为颗粒速度变化曲线图上速度在准备变化的0值与到达最大值后反映在x轴上的距离;颗粒流在不同高度的核心区域坐标:速度极大值时对应的x轴值、选取切片所对应的y轴值、该条速度曲线所对应的高度z轴值。
(3)在碰撞反射阶段,反射的最大高度在0.3~0.4 m,流动形状呈弧形抛物状;从x轴1.5 m左右以后,颗粒流进入了稳定运输阶段,颗粒流的最大高度在0.1~0.15 m,呈现出平稳流动。
根据上述分析的结果,将防尘罩的外形及溜槽结构改进为弧形,且在下落点处右侧反射区再设一段弧形罩。其中,改进后的弧形溜槽与倾斜式溜槽相比,物料在下落过程中并未完全与倾斜式溜槽接触而改进后可以,进而增加了颗粒流下落时在溜槽部分的滑移长度,降低了颗粒流下落速度;弧形防尘罩依据气固两相流的流动规律,避免了因气固两相流与罩面的碰撞角度过大而反冲颗粒流造成粉尘增加,维持了物料的均匀稳定流动。本次改进防尘罩的外形结构如图10所示。
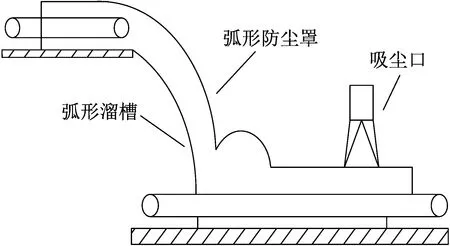
图10 弧形防尘罩
将改进后的弧形防尘罩和柜式、倾斜式防尘罩在同一工况下分别进行数值模拟,计算出罩内粉尘的平均质量浓度如表3所示。改进后罩内粉尘的平均浓度与柜式防尘罩的相比降低了21.6%,与倾斜式防尘罩的相比降低了9.4%,说明改进后的弧形防尘罩可以有效降低粉尘的产生。

表3 防尘罩内粉尘平均质量浓度 mg/m3
4 结论
(1)本研究运用CFD-DEM双向耦合机理,通过Fluent软件和EDEM软件的联合计算进行数值模拟。根据颗粒运动分析和压力流场分析发现,颗粒流在转运点处呈现出3个运动阶段:弧形下落、碰撞反射、稳定运输。
(2)根据气固两相流的流动规律,改进后的弧形防尘罩可以形成均匀稳定物料流,避免剧烈碰撞,可以有效地降低散料在转运过程中产生粉尘。
(3)改进后的溜槽可以完全与物料流接触,能够更大幅度地降低物料颗粒流下落时产生的动能,减少了产尘量和除尘设备的磨损。
(4)研究的不足之处在于设计采用的数据仅为模拟的数据,具有一定的误差,而在实际生产中可根据具体的生产数据进行矫正。
