危险性气体泄漏扩散研究方法对比*
2021-01-19曹杨王红红吕松松李忠涛
曹杨 王红红 吕松松 李忠涛
(中海油研究总院有限责任公司 北京 100028)
0 引言
危险性气体具有易燃、易爆、有毒等特性,泄漏后会诱发火灾、爆炸事故,还会造成环境破坏和人员中毒事件。2015年巴西国家石油公司“Cidade de Sao Mateus”号FPSO天然气泄漏并引发燃爆事故,导致3人死亡、6人失踪。1979 年吉林某化工厂液化石油气罐发生泄漏并引发火灾,造成86 人死亡[1-2]。通过开展气体泄漏扩散的研究,对认识泄漏扩散机理与规律具有重要意义,为安全评价、事故应急救援等提供参考[3-4]。
目前,国外已基本形成了理论—试验—数值模拟为框架的泄漏扩散知识体系。我国的研究起步较晚,对泄漏扩散试验不足,理论模型研究基础薄弱[5],尚未形成一套完整的泄漏扩散的理论框架与知识体系。
笔者试图从目前危险性气体泄漏扩散方面的研究入手进行梳理,通过对现有的研究方法、适用对象、发展特征及内在联系等进行总结与分析,以期对今后我国开展相关研究提供借鉴。
1 发展历程
上世纪中叶,油气泄漏爆炸事故频繁发生,欧美研究机构展开了一系列现场全尺寸气体泄漏试验,尤其是针对重气,目的在于掌握现场气体泄漏扩散情况,为控制泄漏爆炸事故进一步扩大提供指导。
同时,泄漏扩散理论研究也在逐步开展。最初模型为高斯模型,针对连续、瞬时泄漏发展为高斯烟羽模型和烟团模型[6]。为求解扩散系数,Sutton模型被提出[7]。美国运输部曾对高斯稳态烟羽模型修正得到MTB模型,并应用于70—80年代[8]。基于泄漏扩散试验数据,一些学者提出了BM模型[9]。随后,箱模型、板模型、相似模型、浅层模型及三维传递模型等被提出[10],逐步从气团运移整体宏观描述向局部微观探究发展。这一时期的研究是根据不同泄漏条件提出计算模型,其计算程序被相继开发出来。80年代后期,众多数值模拟软件问世,如Fluent、FLACS、Phast等。
另外,相关的试验研究也在开展,如缩小比例试验、风洞试验以及水槽试验,尤其是风洞试验对揭示气体扩散规律、结果验证等起到重要的推动作用[11-12]。
我国在此方面的研究始于上世纪80年代,部分科研院所开展了一系列的风洞试验、水槽模拟试验以及危险化学品泄漏扩散、火灾爆炸、监测监控等研究[13-17]。国内学者还根据已有试验数据,结合数值模拟开展了泄漏扩散规律及验证方面的研究。然而,我国未开展任何全尺寸泄漏试验,在泄漏扩散基础理论研究方面相对薄弱。目前,危险性气体泄漏扩散研究方法主要有数学模型、试验和数值模拟。
2 主要研究方法
2.1 数学模型法
泄漏扩散数学模型[5]是用于描述气体泄漏后在大气范围内的时空分布状况。常见的气体泄漏扩散数学模型、研究对象、适用条件及特点等如表1所示。

表1 泄漏扩散数学模型
从适用对象来看,数学模型从轻质、中性气体,逐渐发展到重质气体。高斯模型在对轻质、中性气体连续源或瞬时源泄漏扩散建模以及浓度时空分布的描述方面有很好的应用。重质气体在泄漏扩散过程中呈现阶段性,并展现出不同的扩散特征。针对重质气体泄漏扩散相继提出了Sutton模型、BM模型、箱模型、板模型、相似模型、三维传递模型等。
数学模型方法演变呈现出以下特点:①通过引入无限分割法,逐渐从整体物理特征描述向内部物理参数描述发展。如箱模型以宏观整体描述为主,而板、相似模型等以微观内部描述为主。②重气扩散研究向方向性及边界问题处理发展。如箱、板模型对径向与侧向扩散速度的研究,云团边界与大气卷吸处理等问题。③复杂大气、地形条件下,重气扩散模型向精细化处理方向发展。如FEM3和MDPG,基于N-S方程等,综合考虑重气下沉、空气卷席及气云吸热等复杂情况进行综合分析与处理。④根据特定泄漏扩散条件和数据更新,衍生新的模型。如Sutton模型是为了解决扩散系数求解而产生的模型,而BM模型是根据试验数据得到的图表关系式,是典型的经验型模型。此外,还产生了SLAB、TWODEE等。
2.2 试验法
(1)全尺寸现场试验
全尺寸现场试验又称为现场大规模试验,以LNG、其他重质气体以及混合气体为研究对象,在特定的气象条件、地形、泄漏源等,对海面、湖面或地面上泄漏扩散过程进行研究。现场泄漏试验是根据真实泄漏情景进行的模拟试验,可提供一手的试验数据,对开展理论研究提供数据支撑[2, 8]。典型现场大规模泄漏试验如表2所示。
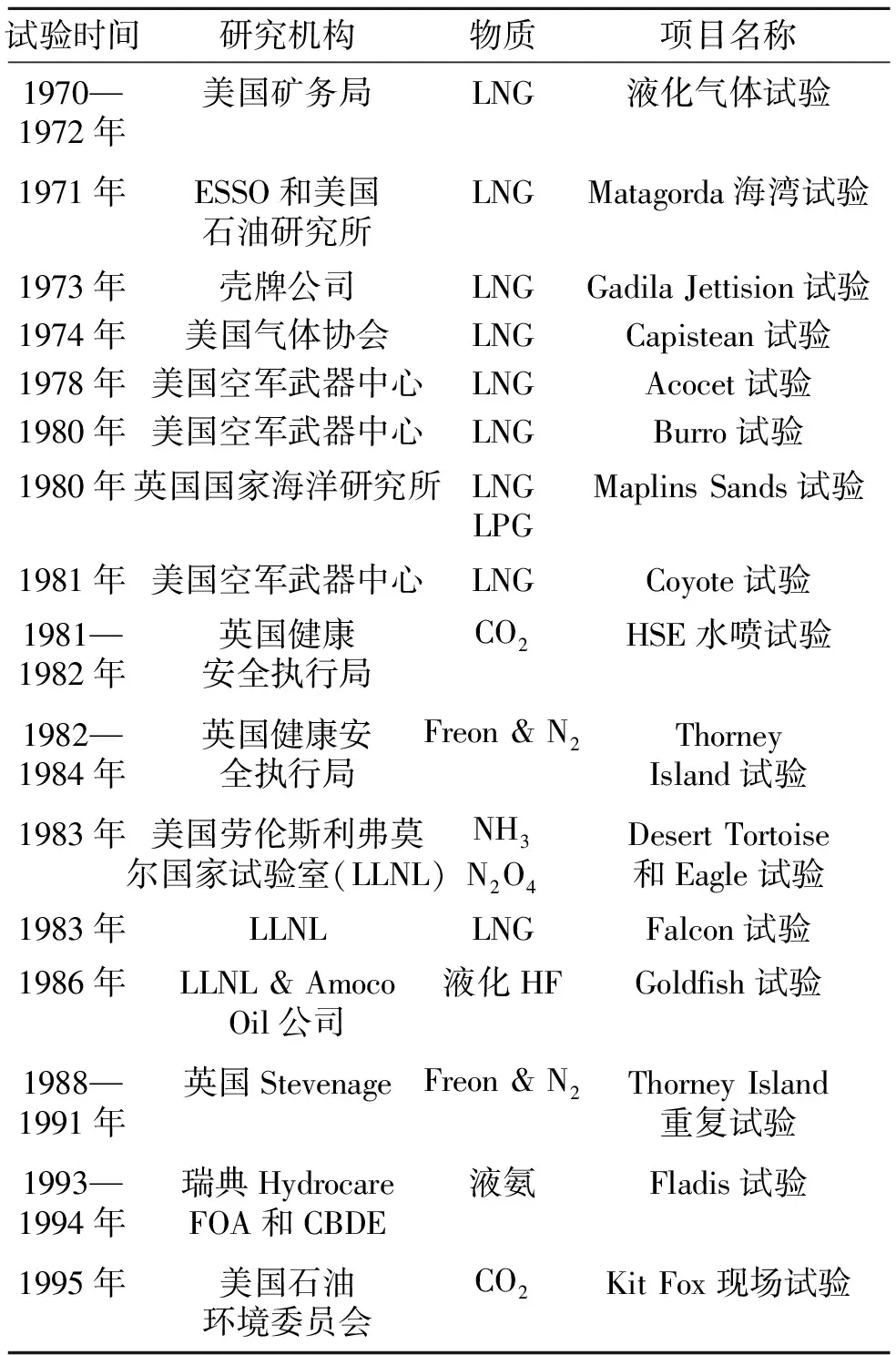
表2 泄漏扩散现场试验
(2)缩小比例现场试验
缩小比例现场试验是根据相似理论将实际扩散模型进行放大或缩小,常用量纲分析法对相关泄漏参数进行缩放,得到试验所需要的泄漏情景参数,再将试验结果还原到实际模型中,得到气体泄漏扩散规律。HALL D J等[11]开展HF缩小比例泄漏扩散试验,并验证了在某些条件下其试验的可行性。DANDRIEUX A等[12]通过开展缩小比例试验研究了扇形水幕对氯气泄漏扩散的影响作用。施志荣[18]通过缩小比例模型试验研究了有害气体的扩散规律,结合CFD模拟结果进行了对比分析。XING J等[19]和宁平等[20]通过缩小比例模拟试验研究了CO2发生喷出后的浓度场分布,并对试验结果进行了模拟验证。
(3)室内试验法
室内试验法主要有风洞试验法和水槽试验法。
风洞试验[21]是根据相似理论,将气体泄漏扩散场景实物按照一定的相似比缩小,并根据风洞试验模拟结果按照相似准则对应到大尺度气体泄漏扩散现场原型。
MERONEY R N等[21]在1∶28.9比例风洞模型中开展了不同泄漏条件下LNG扩散过程模拟,研究过程中提出了弗劳德数。HEIDORN K C等[22]通过风洞模拟试验研究无风或微小风条件下,障碍物对重气烟团扩散行为影响。ROBERTS P T等[23]研究了表面粗糙度对重气扩散的影响。SWEATMAN W L等[24]研究了重气瞬时源泄漏下,泄漏量及浓度随时间变化的问题。HAVENS J等[25]通过风洞试验研究了在均匀障碍物影响下,不同泄漏量、风速条件时CO2的扩散速度以及浓度变化规律。ROBINS A等[26]研究了中性、稳定层结及不同粗糙度的烟羽扩散规律。CHRC中心开展了低风速或超低风速的重气泄漏扩散试验,研究了在设置障碍物情况下LNG泄漏扩散行为[27]。
我国部分科研院所开展了风洞模拟试验,研究重气瞬时源、连续源扩散行为。倪章松等[15]对工业区有毒有害气体扩散规律进行了风洞试验研究。杜可[16]、刘国梁[27]以风洞试验为手段,探究瞬时源、重气烟羽扩散特征以及围墙和树对其扩散行为的影响。沈武艳[17]通过风洞模拟试验开展了高原山区城市重气泄漏扩散规律的研究。姜传胜等[28]还将重气连续泄漏的风洞模拟实验结果与SLAB重气扩散模型的预测结果进行了对比。
水槽试验法主要是利用水槽模型,通过研究不同密度液体的流动状态来模拟气体扩散规律。秦颂等[29]、蒯念生等[30]研究了重气在盐水中的扩散规律。
(4)不同类型试验法的对比
针对危险性气体泄漏扩散不同类型试验研究情况进行总结及分析,具体如表3所示。
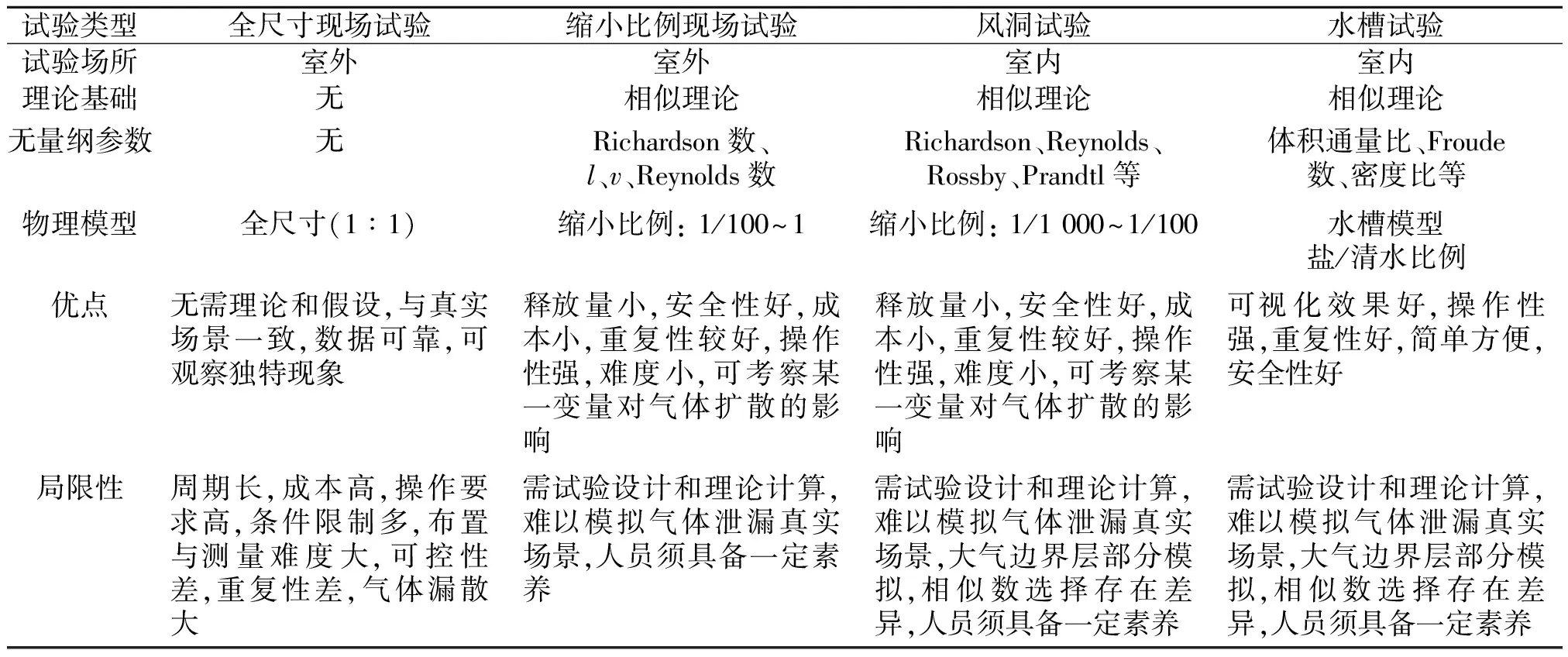
表3 不同类型试验法的对比
由表可见,危险性气体的试验研究有以下特征:①试验模型尺寸逐渐缩小。从室外全尺寸、大规模试验到室内水槽试验,试验规模越来越小,从室外转到室内,成本、周期逐渐减小,可操作性、重复性逐渐变强。②试验理论性不断加强。全尺寸泄漏试验无需任何理论推导,而缩小比例、风洞及水槽试验都需进行相似理论计算,所需无量纲参数也不同。③试验研究对象范围进一步扩大。从LNG、LPG、CO2到Freon与N2混合,泄漏物质从重质气体到中性气体,从单一物质到混合物质,水槽试验更是用液体扩散代替气体研究,泄漏量逐渐变小,从有毒到无毒,研究对象呈现出多样性。④试验模拟的场景越来越复杂。从简单泄漏场景逐渐向复杂泄漏条件发展,如全泄漏LNG试验多在海、湖面,缩小比例试验多在平坦陆地,风洞试验多模拟复杂地面、存在障碍物分布以及不同粗糙度的泄漏扩散,边界条件处理上逐渐细化,试验研究向复杂化、精细化方向发展。
2.3 数值模拟法
数值模拟方法与数学模型的提出和发展密不可分。泄漏扩散理论、试验的深入开展,为泄漏扩散计算模型的构建和设计提供大量理论基础和数据资料。随着箱模型和相似模型的提出,对气体扩散的研究从简单、均匀的宏观整体特征,转向气团内部物理参数的细致考究。许多计算模型在箱模型基础上被开发,如CRUNCH、SOURE、II T Heavy Gas等模型用来计算瞬态连续释放的重气扩散[31-34]。TERIELE P H M[35]开发了稳态条件释放源地面烟羽浓度数值模型,壳牌以此开发了HEGADAS。ZEMAN发展了SLAB模型,用于模拟气团扩散的3D特征[36]。WURTZ J等[37]、HANKIN R K等[38]开发了DISPLAY I II Model、TWODEE等模型,但这些模型受假设条件的影响,对特别复杂的边界条件,模拟结果存在不准确性和不确定性。三维传递模型进一步完善了数值模拟,通过引入N-S方程,使其更适用于三维非定常湍流的模拟。
数值模拟方法的发展呈现以下特点:①数值模拟发展主要基于理论模型的创新,新的气体扩散数学模型提出为数值计算模型开发提供了理论基础和框架。②数值模拟向复杂化、精细化计算发展。数值模拟从简单一维模型发展到复杂三维模型,还能对复杂地形条件、泄漏条件情景模拟,对非定常条件湍流进行描述。③数值模拟向交叉方向发展。数值模拟过程中还需结合有限差图解法、有限空间理论以及静、滞流体力学相关理论等方法和学科[39]。
2.4 研究方法间的内在联系
危险性气体泄漏扩散研究方法之间存在相辅相成、相互验证的关系。数学模型为开展相关试验提供理论基础和指导。试验开展验证了数学模型的适用性与准确性,也反映其存在的问题,作进一步改进。试验中可能出现新的扩散现象,会衍生出新的数学模型,丰富了泄漏扩散理论。数值模拟使得复杂的数学模型计算成为可能,并提高计算速度,避免人工计算带来的误差与错误。对泄漏扩散物理模型构建、边界条件及计算模型的要求朝着真实化、精细化、精确化方向发展。泄漏扩散试验的开展及其结果,为数值模拟结果验证提供了数据支持,同时对边界条件设置和参数选择提供了经验和参考。危险性气体泄漏扩散研究方法之间的内在联系如图1所示。
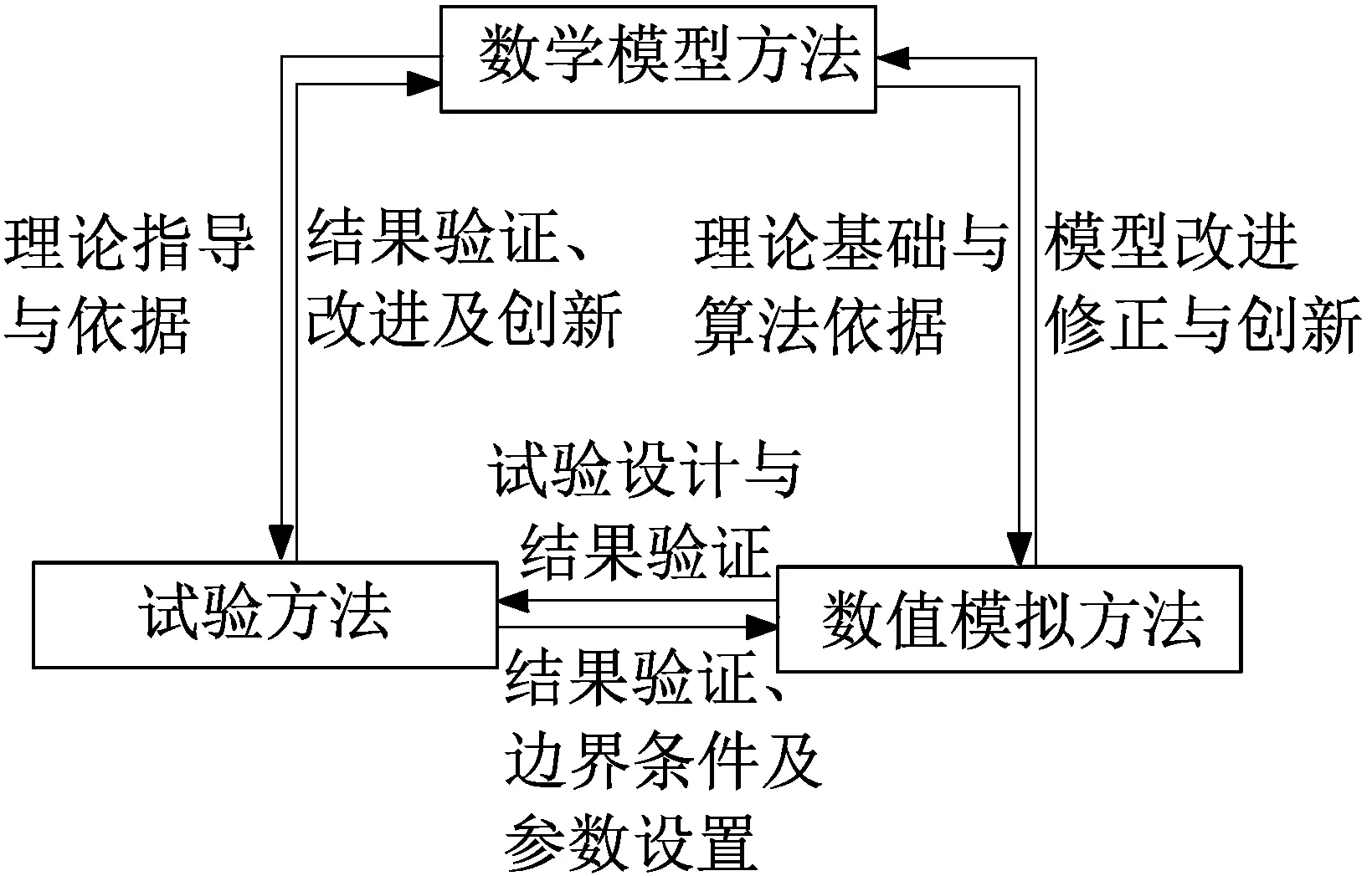
图1 危险性气体泄漏扩散研究方法之间的内在联系
3 结语
(1)应加强在气体泄漏扩散理论和试验方面的研究,提出适用于国内发展的泄漏扩散理论模型。
(2)应开展低风速、复杂地形、倾斜表面条件下,考虑大气湿度、太阳辐射因素的泄漏扩散模型研究,以及多组分气体成分及其伴有化学反应过程、非稳态重气及多组分重气泄漏扩散方面的研究。
(3)应开展精细化数值建模研究,须做好现场调研,掌握清楚现场设备设施尺寸、数量及布置情况,为后期精确建模奠定基础。
