基于几何参数标定的串联机器人精度提升
2021-01-19赵艺兵温秀兰乔贵方吕仲艳宋爱国康传帅
赵艺兵, 温秀兰, 乔贵方, 吕仲艳, 宋爱国, 康传帅
(1.南京工程学院 工业中心 创新创业学院, 江苏 南京 211167; 2.南京工程学院 自动化学院,江苏 南京 211167; 3.东南大学 仪器科学与工程学院,江苏 南京 210096)
1 引 言
我国于2017年启动实施“智能机器人”重点专项计划[1],指出工业机器人应用于高端制造领域时,其绝对定位精度应优于 0.05 mm,姿态角应优于0.1°。目前,尽管工业机器人的重复定位精度较高,能满足示教编程的需求,但绝对定位精度还较低,难以满足机器人在精密加工、精密检测、精准医疗等高精尖制造业的迫切需求。通过对机器人实测标定可以有效提高机器人末端定位精度。标定通常分为以下3级:一级标定也称为关节级标定,主要是对驱动器和关节传感器机构的运动学进行标定,其目的是确定关节位移传感器产生的信号和关节实际位移之间关系;二级标定也称为机器人几何参数标定,即确定机器人的几何参数模型与机器人关节角之间关系;三级标定也称为非几何参数标定,非几何参数误差主要包括关节柔度、摩擦、间隙及连杆变形等。大量研究结果表明:影响机器人作业精度的主要误差源于几何参数误差,占到总误差的80%~90%,通过对机器人几何参数标定能够在不改变硬件结构或控制器前提下通过校正软件快速实现机器人绝对定位精度提升[2~4]。
机器人几何参数标定包括建模、测量、辨识及补偿4个过程。机器人建模是标定的基础,目前最常用的几何参数模型是基于齐次变换矩阵的DH模型,该模型首先在机器人的每个连杆上建立一坐标系,利用相邻连杆间变换矩阵计算得到末端执行器的位置和姿态。因该模型连杆坐标系原点位于关节轴线与关节轴线公法线的交点,当两轴线平行或垂直时轴线的微小变化会导致机器人几何参数变化很大甚至到无穷,不满足机器人标定时要求模型具有连续性要求,模型存在奇异性,影响标定结果的准确性。为了解决该问题,Hayati S A提出了改进的DH模型(MDH模型)[5],当相邻关节轴线平行时增加一个旋转参数,弥补了DH模型的不足;但当相邻两轴线垂直或接近垂直时,该模型仍具有奇异性,影响机器人标定的准确性[6]。为满足标定模型具有完备性与连续性要求,文献[7]在DH法建立的杆件坐标系上研究了6参数串联机器人的误差模型。文献[8, 9]研究了通过建立指数积模型对串联机器人几何参数进行标定,取得较好效果。辨识是从测量数据中获取机器人实际模型参数信息的过程,辨识结果的准确性直接影响其定位精度。传统的辨识方法有最小二乘法、Levenberg-Marquardt算法、卡尔曼滤波法等。近些年智能计算得到长足发展,先后出现遗传算法、免疫进化计算、微分进化、蚂蚁算法、粒子群算法等,已有学者尝试将智能计算应用于对机器人几何参数标定取得了较好效果[10~14]。文献 [10]建立了6自由度机器人的MDH模型,通过计算种群的适应值按照赌轮法选择个体,根据事先设定的概率进行交叉和变异操作,通过仿真验证算法的有效性。文献[11]将粒子群优化算法用于对神经网络初始权值和阈值优化,实现机器人综合精度补偿,用来提高飞机自动化装配精度。文献[12]采用扩展卡尔曼滤波对机器人几何参数辨识,采用人工神经网络对连杆变形、关节柔性、齿轮间隙等无模型的非几何参数误差进行补偿来提高PUMA和HH800机器人精度。文献[13]研究了基于量子粒子群优化算法的机器人几何参数标定方法,选用五轴并联机床的平面约束机构为试验对象验证了算法的有效性。文献[14]采用深度神经网络辨识机器人非线性残余误差,通过现场优化机器人焊接轨迹实验来验证算法的有效性。
针对机器人相邻两轴线垂直及接近垂直时,常用DH模型、MDH模型存在奇异性,本文研究建立了串联机器人的零参考模型,该模型其零位可以任意选取,基于位置相似性原理,通过递归方程计算获得末端位姿封闭形式的解,非常适用于关节臂依次相连的串联机器人。根据该模型标定机器人几何参数误差特点,提出了基于改进遗传算法实现机器人几何参数标定,以提高机器人定位精度。
2 机器人几何参数标定的数学模型
2.1 零参考模型
建立串联机器人的零参考模型(zero reference model,ZRM)如图1所示。Oxyz为机器人基坐标系,ηi为机器人方向矢量,ρi+1为连接矢量,i=1,2,…,n,n为机器人关节数目。机器人零位时的方向矢量和连接矢量表示为η0i和ρ0i+1,即为机器人的名义几何参数,可从机器人手册中获得。
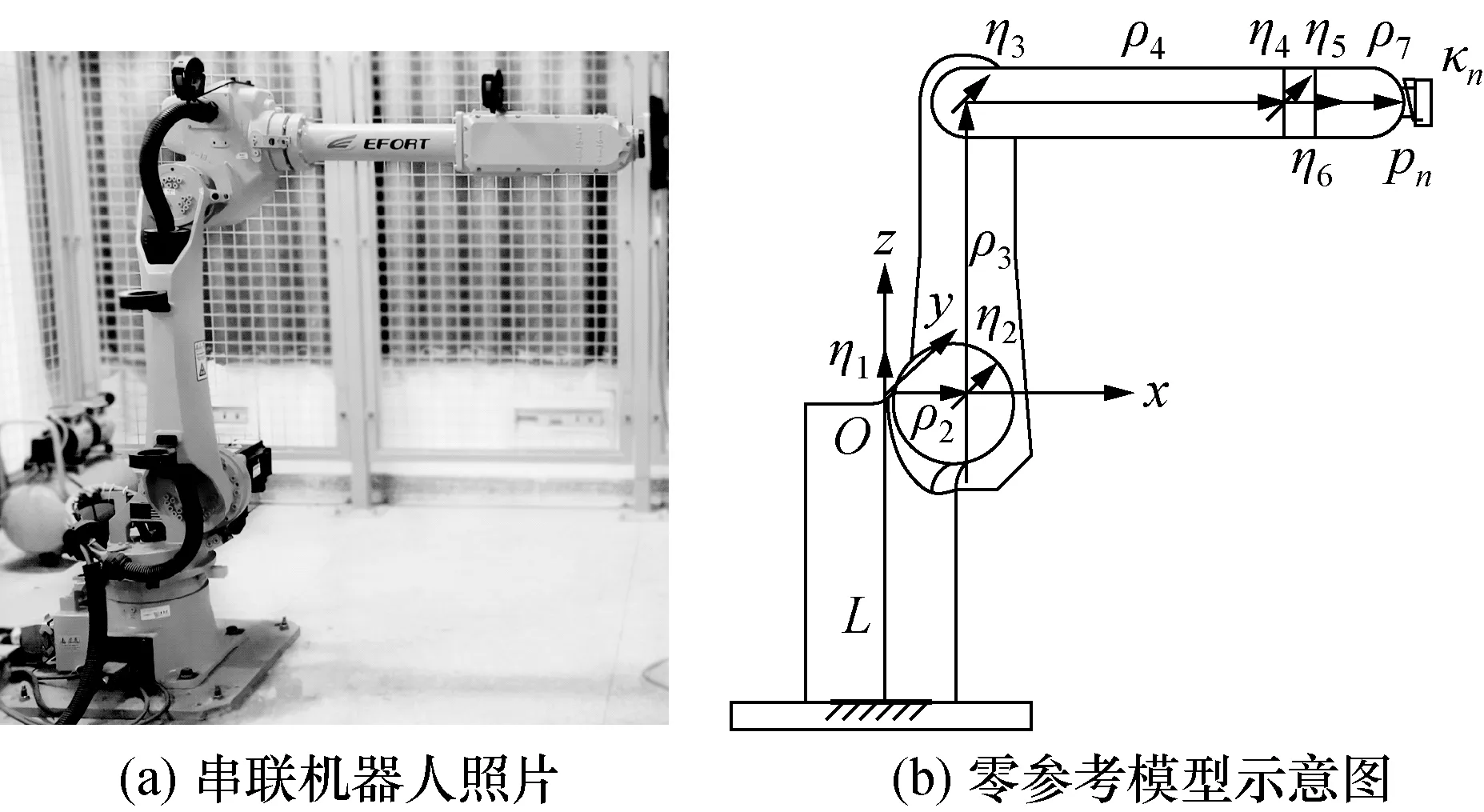
图1 零参考模型Fig.1 Zero reference model
任意位置时的ηi,ρi+1与η0i,ρ0i+1具有如下关系:
ηi=κiη0i,ρi+1=κiρ0i+1
(1)
式中:κi为串联机器人的旋转矩阵[15],可表示为
(2)
其中,矩阵R(qi,η0i)表示关节角qi绕轴线η0i旋转,计算公式为:
R(qi,η0i)=
其中,Vi=1-cos(qi),Si=sin(qi),η0ix,η0iy,η0iz分别表示η0i在x,y,z方向的分量。
2.2 标定模型
具有n个旋转关节的串联机器人其末端姿态和位置可由旋转矩阵κn和平移矩阵Pn表示为[16]:
(3)
(4)
由式(3)和式(4)可见,κn和Pn是关节角qi及机器人几何参数η0i和ρ0i+1的函数,当机器人零位状态的方向分量沿x,y,z轴有微小误差δη0ix,δη0iy,δη0iz时,引起R(qi,η0i)的误差为δR(qi,η0i):
δR(qi,η0i)=κxiδη0ix+κyiδη0iy+κziδη0iz
(5)
误差δR(qi,η0i)将引起机器人末端姿态旋转矩阵κn产生误差δκn,可表示为:
(6)
由几何参数误差δη0i、δρ0i+1引起的机器人末端位置变化为
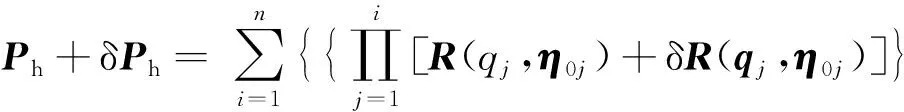
[ρ0i+1+δρ0i+1]}
(7)
由式(6)和式(7)可知,若存在几何参数方向分量误差δη0ix、δη0iy、δη0iz及连接分量误差δρ0i+1x、δρ0i+1y、δρ0i+1z,则导致末端姿态及位置发生变化δκh和δPh。
设由机器人名义几何参数经公式(3)和公式(4)计算得到末端姿态和位置的名义旋转和平移矩阵分别为κhn和Phn,根据激光跟踪仪测得末端在基坐标系下绕x、y、z轴的姿态坐标及沿x、y、z轴的位置坐标求得末端姿态和位置的测量旋转矩阵κhm和平移矩阵Phm,则末端姿态和位置的旋转误差矩阵δκh和平移误差矩阵δPh计算如下[17]:
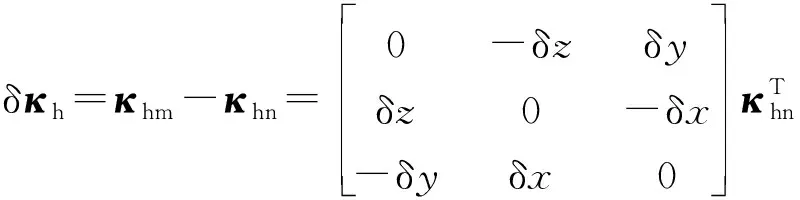
由几何参数误差引起机器人末端姿态和位置变化的关系式可表示为[16]:
(8)
其中Je为 (6+n)行6n列Jacobian矩阵,
δη0=[δη01xδη01yδη01z… δη0nx]T,
δρ0=[δρ02xδρ02yδρ02z… δρ0n+1x]T。
2.3 目标函数
采用IGA优化搜索机器人几何参数误差时,定义其目标函数f为:
(9)
(10)
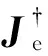
由此可见,目标函数f是几何参数误差[δη01xδη01yδη01z… δη0nx, δρ02xδρ02yδρ02z… δρ0n+1x]的函数,机器人几何参数标定实质是通过优化算法搜索一组几何参数误差集,使末端位姿误差为最小,属于多变量复杂优化问题,非常适合用改进遗传算法来求解。
3 改进遗传算法实现几何参数标定
3.1 编码
采用遗传算法优化搜索机器人几何参数误差旨在找到目标函数最小值,从而提高机器人末端定位精度。考虑到几何参数误差标定待优化变量多,且数值连续,为提高优化精度和效率,采用实数编码,每一个基因代表一个待优化变量,所有变量对应的基因依次连在一起构成该实数编码的个体。
设优化问题为最小化问题:
(11)
式中:f为目标函数;S=(s1,…,sl,…,sp)表示一个个体,其中sl(l=1,2,…,p)为待优化变量,p为优化变量的数目;al、bl分别为变量sl的上下界。
如图1所示6自由度串联机器人,待优化个体S表示为6个关节的几何参数误差集[δη01xδη01yδη01z… δη06z, δρ02xδρ02yδρ02z… δρ07z],采用IGA同时搜索上述几何参数误差,完成标定。
3.2 交叉操作
考虑到机器人ZRM几何参数标定其目标函数中待优化变量不仅彼此独立,而且变量数值均较小,因此采用混合交叉策略(BLX-α)[18],算法如下:
(1)从种群中随机选取两个父代个体S1、S2;
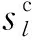
(12)
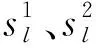
3.3 机器人几何参数标定流程
为保持群体多样性,IGA实现时采用基于代沟最小的代选择模型,具体步骤如下:
step 1.设置进化代数t,随机产生M个初始个体,构成初始种群;
step 2.从群体中任意选取两个个体S1、S2作为父代;
step 3.将S1、S2采用BLX-α交叉产生nc个子群体;
step 4.计算S1、S2和nc个子群体的目标函数值;
step 5.从S1、S2和nc个子群体中选择目标值最小的两个个体替换原父代S1、S2;
step 6.判断是否满足终止条件,若不满足,则t=t+1,转Step 2;否则输出优化所得几何参数误差;
step 7. 根据优化得到的几何参数误差误差计算标定前后机器人末端绝对位置和姿态误差。
4 实验与结果
4.1 仿真实验
4.1.1 位姿产生
6自由度串联机器人在工业中应用最多,为了验证算法的有效性,选择图1所示ER10L-C10的6自由度串联机器人作为实验对象,从使用手册中获取该机器人零参考模型名义几何参数见表1。
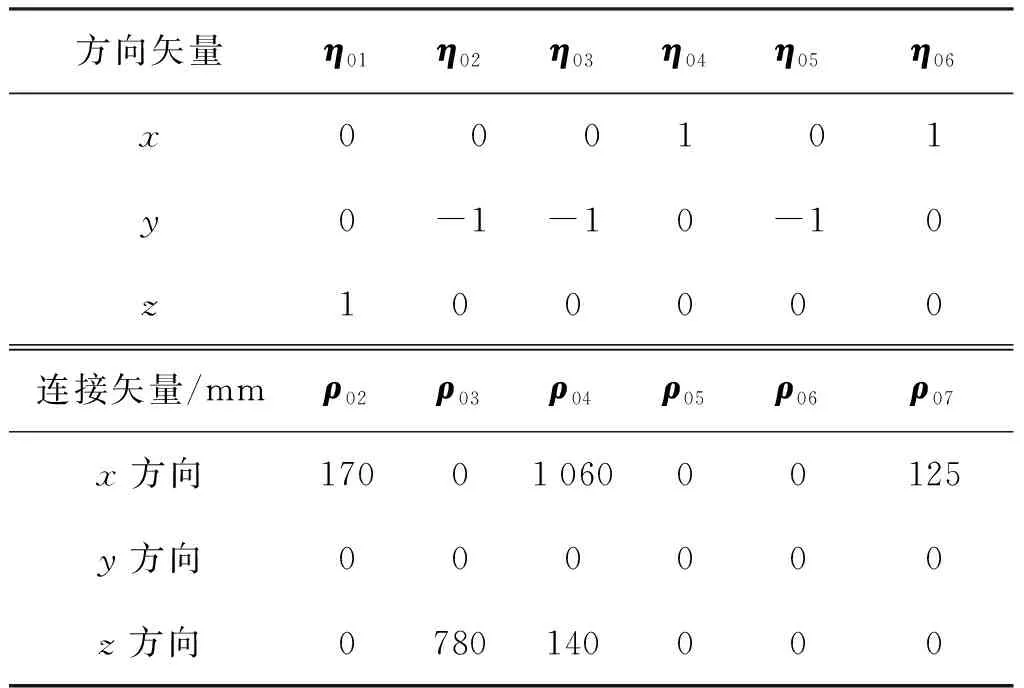
表1 ER10L-C10机器人名义几何参数Tab.1 Nominal geometric parameters of ER10L-C10 robot
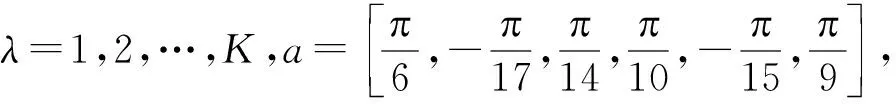
考虑到因机器人加工、装配、磨损等误差会导致由机器人示教器设定的关节角与实际关节角间存在误差,实际关节角产生为在名义关节角上加入±0.001 rad均匀随机噪声。由关节角及几何参数的名义值和实际值根据第2.2节公式即可计算出机器人末端姿态和位置的名义值、实际值及姿态与位置误差。考虑到在测量机器人末端位姿时存在测量误差,在由上述公式计算获得的末端姿态和位置实际值上分别加入均值为计算值,方差为0.01 rad和0.5 mm的正态分布随机误差,得到末端姿态与位置的测量仿真值。
4.1.2 实验结果
根据上述随机设定的几何参数误差和关节角,采用提出的IGA优化求解机器人几何参数误差,其中种群和子代种群规模均设定为10,算法终止条件设定为最大进化代数1000。在Intel(R) Core(TM)i5-4570 CPU主频3.20 GHz计算机上采用Matlab R2015b在设定的标定点N=4,8,16,32,48,64等6组不同关节角下完成1000代进化所需时间分别为 78, 145,280,546,830,1140 s。图2同时绘制了N=4,8,16,32时的进化过程图,表2给出了在上述设定的不同组关节角下机器人末端位置和姿态标定前后误差比较结果,其中AOE为平均绝对姿态误差,为平均绝对位置误差,MOE为最大绝对姿态误差,MPE为最大绝对位置误差。
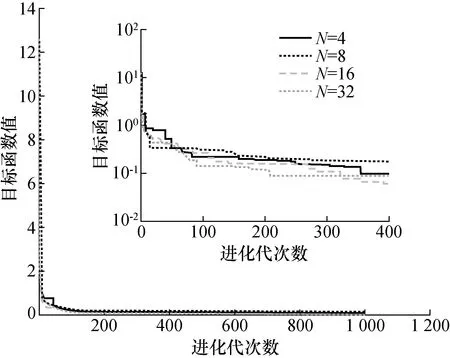
图2 进化过程图Fig.2 Evolution process figure
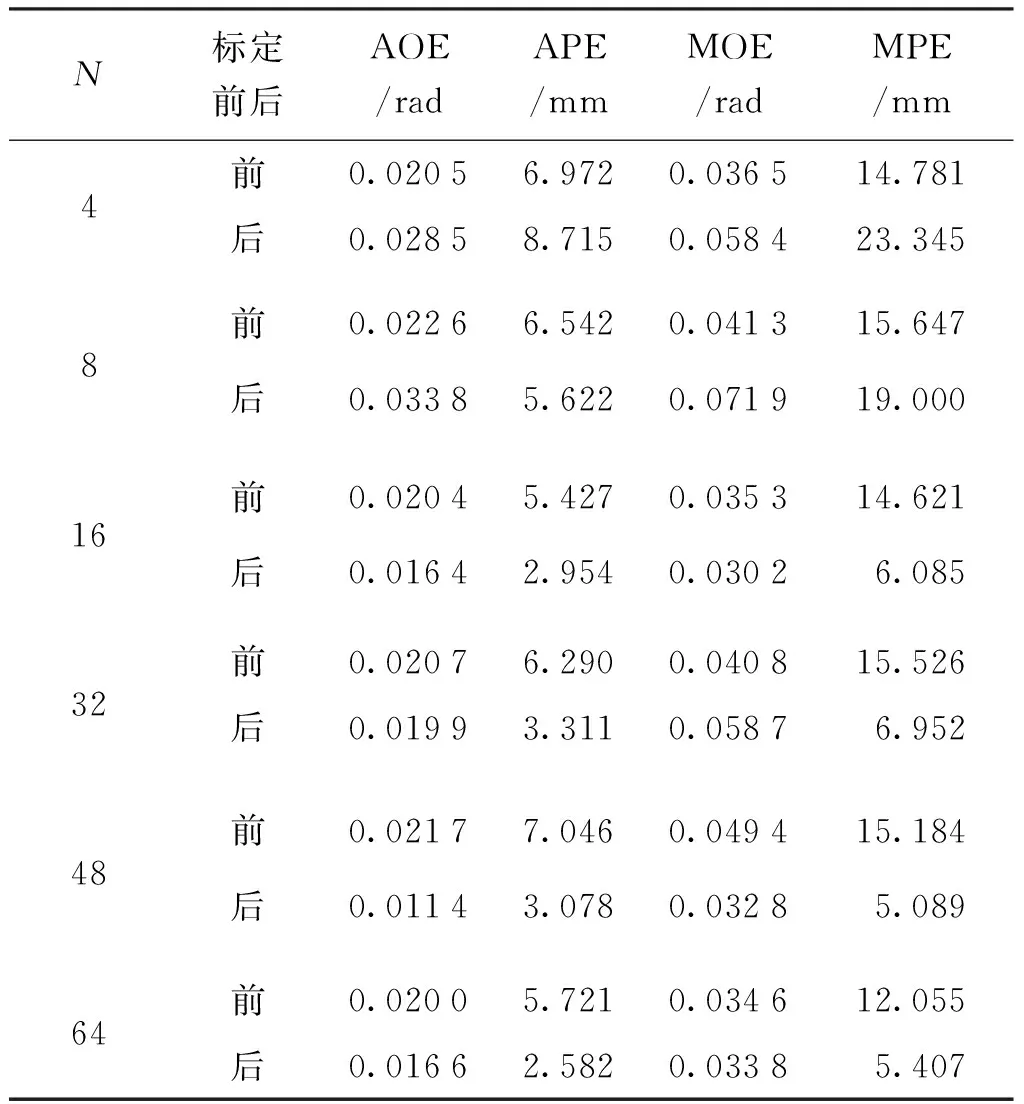
表2 预先设定误差与标定后误差比较Tab.2 Comparison between the pre-assumed and post-calibrated pose errors
由图2和表2可见,提出的IGA能够快速完成机器人ZRM几何参数标定,机器人在设定的不同标定点下其末端定位精度均有大幅提升。为了验证经标定后的机器人其精度提升的泛化能力,针对设定的6组标定点,分别在机器人整个工作空间内随机产生40组关节角,根据不同标定点下优化得到的机器人几何参数值计算末端测试点在标定前后位置误差见表3。
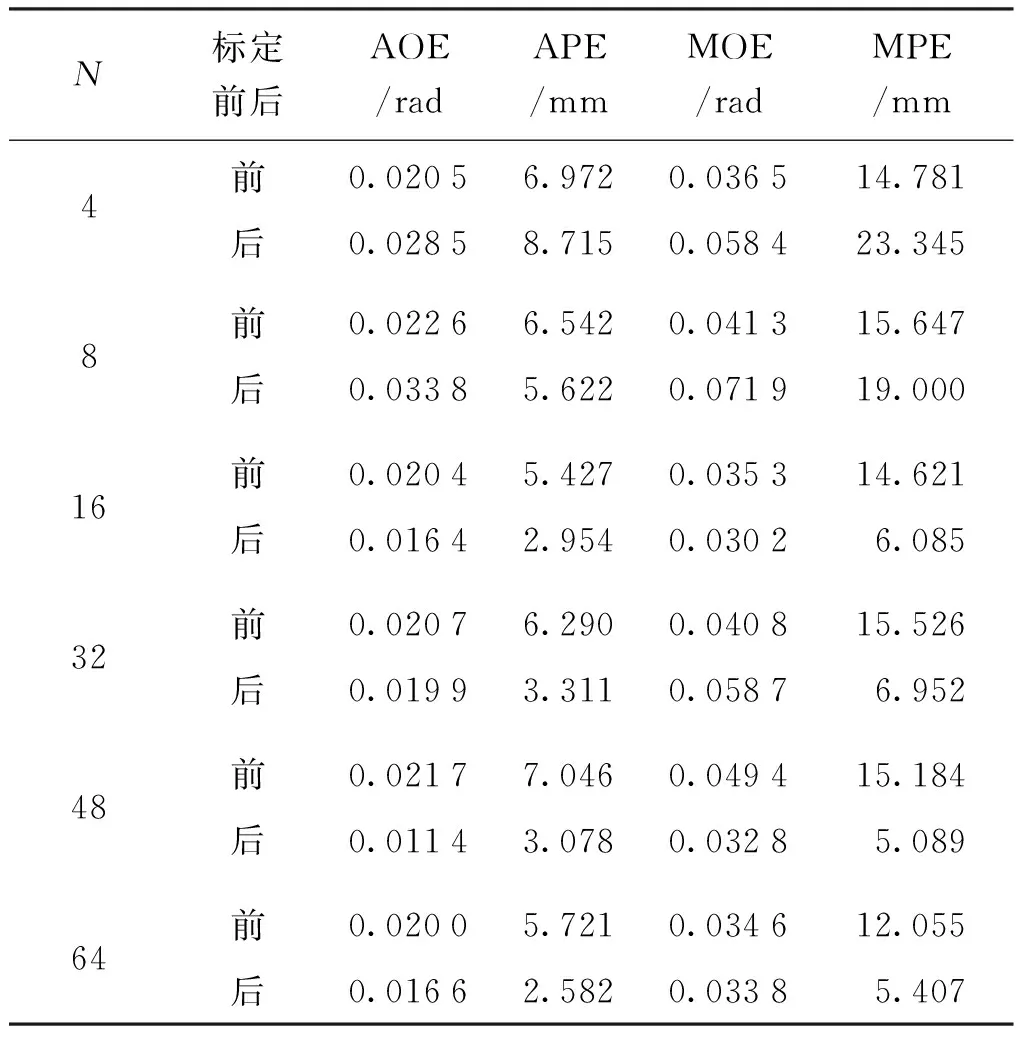
表3 整个工作空间内误差比较Tab.3 Errors comparison in the whole workspace
由表2和表3可见,在标定点N为4和8时,尽管标定效果很好,但随机产生的测试点精度提升效果差,随着N增加,测试点精度提升效果逐步改善,当标定点取为48时,其测试点平均和最大绝对定位误差由标定前的7.046 mm和15.184 mm分别改善为标定后的3.078 mm和5.089 mm,精度提升效果最佳;当标定点进一步增加时精度提升效果趋于稳定。因此,在对机器人实测标定时建议标定点设定为50个左右为宜,随机产生的测试点其精度提升泛化能力强。图3给出了N=32和N=48时,测试点标定前后绝对位置误差的结果对比。
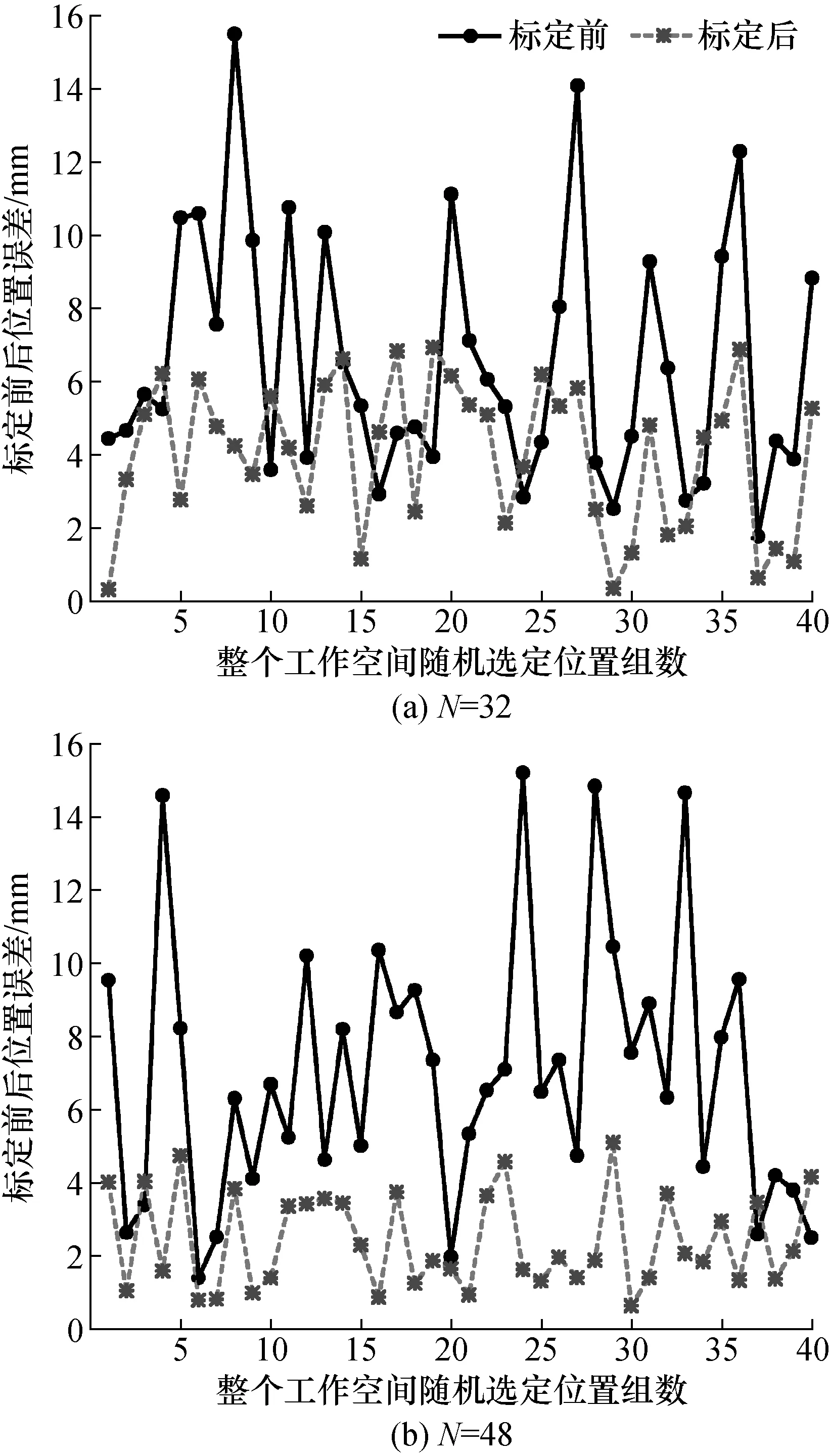
图3 仿真测试点位置误差比较Fig.3 Position errors comparison of simulation test points
4.2 实测标定
对实验室ER10L-C10机器人标定实测环境如图4所示,该机器人末端负载为0~10 kg,重复定位精度为±0.05 mm,测量由Leica AT960激光跟踪仪、TMAC探测器、上位机及Spatial Analyzer(SA)软件共同完成,TMAC安装在机器人末端的法兰上,Leica AT960空间测量精度为15 μm+6 μm/m,能够同时测量机器人末端的位置和姿态,对温度、湿度及压力的变化具有自检和补偿功能。测量过程严格按照ISO 9283即GB/T 12642-2013[19]工业机器人性能规范及其试验方法标准执行。

图4 ER10L-C10标定实测环境Fig.4 Real measurement setup for ER10L-C10 calibration
在SA软件中设置机器人的基坐标系为参考坐标系,以坐标值(1 300, 0, 900)为中心点,在边长1 500 mm的正方体工作空间内随机生成50个标定点的末端位置和姿态及对应的关节角,采用提出的IGA方法对ER10 L-C10几何参数误差进行标定,其中方向分量误差和连接分量误差分别在[-0.01,+0.01]和[-0.5,+0.5]区间内均匀随机产生,计算标定前后的绝对位置误差如图5所示,其最大和平均绝对位置误差由标定前的8.683 5 mm和5.579 1 mm分别降为标定后的1.368 3 mm和0.376 4 mm,定位精度有大幅提升。
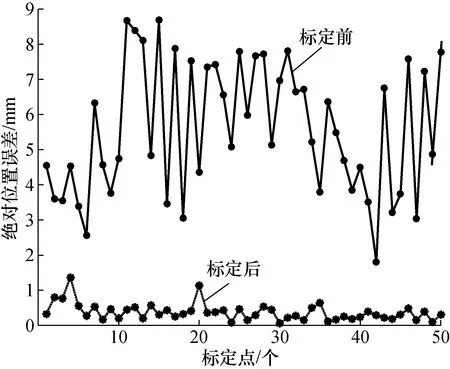
图5 ER10 L-C1050个标定点绝对定位误差Fig.5 APE of 50 calibration points for for ER10L-C10
为了验证经标定后机器人精度提升的泛化能力,在上述正方体工作空间内重新随机生成100个测试点,用已标定好的几何参数计算测试点标定前后的绝对位置误差如图6所示,由图可见,测试点最大和平均绝对位置误差由标定前的8.931 7 mm和5.917 2 mm分别降为标定后的1.213 7 mm和 0.452 7 mm, 平均定位精度提升了92.3%,证实了提出方法对随机产生测试点精度提升泛化能力强。
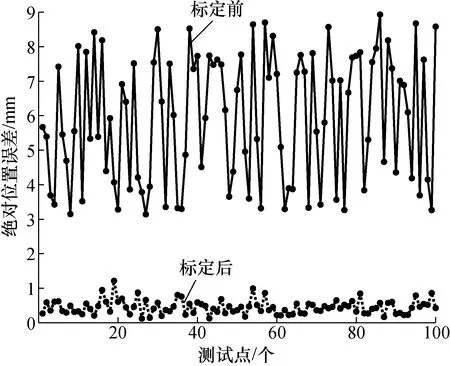
图6 ER10L-C10100测试点绝对定位误差Fig.6 APE of 100 test points for for ER10L-C10
5 结 论
针对当机器人相邻两轴线垂直及接近垂直时常用模型存在奇异性问题,建立了包含方向矢量和连接矢量的串联机器人零参考模型,提出了用改进遗传算法优化求解零位方向分量和连接方向分量,大量实验结果表明:(1) 所建机器人零参考模型满足标定模型连续性要求,避免奇异点出现;(2) 对机器人进行几何参数标定时,标定点数取为50点左右最为适宜,标定效果最佳;(3) 对ER10L-C10机器人,采用提出的IGA对其ZRM几何参数误差标定后,该器人在整个工作空间内末端定位精度平均提升约90%,适于在有高精度定位要求的串联机器人几何参数标定中推广应用。
