基于MATLAB与COMSOL联合仿真的梯形迷宫滴头流道优化

胡宇祥，彭军志，殷 飞，刘喜峰，李 娜

（吉林农业科技学院，吉林 132101）

0 引 言

滴灌灌水器是滴灌系统中最为关键的元件，其使用过程中蒸发损失小，不产生地面径流，几乎没有深层渗漏。随着农业用水形势逐年严峻以及国家“节水增粮行动”项目的大力推广，滴灌技术成为最有效的灌溉方式，是保障增产增收的重要手段[1]。滴灌灌水器结构尺寸对滴灌系统灌水的均匀性、抗堵塞能力影响显著。过大的流道结构参数将造成灌溉均匀度下降，过小的流道结构参数将造成灌水器流道堵塞，严重时会使整个系统无法正常工作[2-3]。因此，研究流道结构参数与滴头水力性能之间的关系一直是节水灌溉领域的研究热点。

目前，国内外学者已在滴灌灌水器流道结构参数优化方面取得了一系列的研究成果，颜廷熠等利用正交试验法，研究了流道结构参数对滴头水力性能的影响[4-6]；王文娥利用 FLUENT 软件对内镶齿形片状滴头的水力性能进行了数值模拟，获得了滴头压力-流量关系式并分析了滴头内速度、压力分布[7]；李永欣等建立了迷宫滴头的CFD数值模型，并对滴头的压力流量关系、流道内部的压力和流速分布进行了数值模拟计算，利用原型滴头和滴头放大模型实测值对模型和模拟计算结果进行了试验验证[8]；陈爱平利用 GAMBIT软件建立了输送管的仿真模型，通过 FLUENT 软件的数值模拟计算，得到了不同滴灌装置输送管结构参数下的流场分布特性[9]；Souza等通过试验方式，设计了一种灌溉滴头，测定了滴头流量系数和流态指数[10]；Li等利用多元回归分析，建立了流量与流道几何参数之间的线性回归方程[11]；Wei等利用CFD对滴头水利特性进行了仿真研究[12]。目前，上述研究多是利用正交试验方法，将流道结构参数设计成多因素多水平的试验，通过CFD 方法或者试验法获得滴头的宏观水力特性，即压力与流量间的关系，分析流道结构参数与流态指数之间关系[13]。但是通过正交试验设计进行数据分析后得到的优选结果，只是因素间不同水平的相互组合，难于确定数据变化规律。水平设计的少，则自变量定义域不完整，试验设计具有随机性，结果不够精确[14-15]；如果水平设计的多，则试验数据体量大，试验次数多，尤其是费用昂贵的试验，弊端更加凸显。因此，需要一种能够快速准确求解灌水器流道尺寸的计算方法。

鉴于此，本文提出联合MATLAB与COMSOL仿真软件进行滴灌灌水器流道参数优化设计，采用COMSOL软件对梯形迷宫流道灌水器进行仿真，求解最佳流态指数下的滴灌灌水器结构参数，研究流道齿参差值、齿高、单元数、流道转角、齿间距这5个变量对灌水器流道参数的影响，并在此基础上建立数学预测模型，以期为快速确定灌水器流道结构参数提供理论依据以及科学参考。

1 研究方法

1.1 滴灌灌水器流道数学模型

1.1.1 设计变量

迷宫形滴头相比贴片形式滴头抗堵性能好，灌水均匀，滴头整体性强。Netafim公司作为滴灌技术的发明者，一直在引领滴灌领域技术变革。本文以该公司迷宫滴头流道参数的取值范围作为参考依据，其流道结构如图1所示。

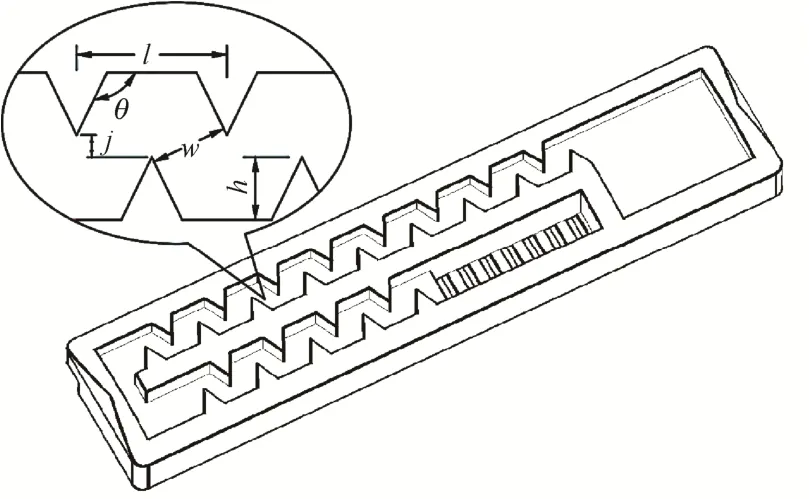
图1 灌水器流道结构及参数示意图Fig.1 Schematic and parameter diagram of emitter channel

本文选取梯形迷宫流道滴头进行研究，影响其水力性能的关键结构参数包括流道宽度w、流道转角θ、齿高h、齿间距l、齿参差值j，灌水器流道单元数n。θ、h、l、j、n这5个参数可以确定梯形齿道单元平面形状，流道宽度w按式（1）计算[16-17]。

算例中，流道转角θ、齿高h、齿间距l、齿参差值j和流道单元数n是设计变量。根据已有的研究文献，各变量取值范围如表1 所示[13]。

表1 灌水器的结构参数取值范围Table 1 Range of structural parameters of emitter

1.1.2 目标函数

滴灌滴头的流态指数x表示流量对压力发生改变的敏感程度，流态指数越小，滴头的水力性能越好[18]。x=1表示流量变化与压力以相同的百分率变化，x=0表示流量不随压力变化而变化。压力补偿式灌水器，流态指数趋近于0；非压力补偿式灌水器，流态指数介于0～1之间。非压力补偿式灌水器x值越趋近于0.5，流量对压力敏感程度就越小，水力性能越优异[19]。因此，建立目标函数如式（2）所示，要求非压力补偿式灌水器流态指数趋近于0.5，保证灌水器水力性能，提高出流均匀性。

式中F为目标函数；x为流态指数，按照SL/T67.1—94要求，可由流量与压力关系[20]计算得出：

式中Q为滴头流量，L/h；H为工作压力， kPa；x为流态指数；Kd为流量系数。从0.5～1.5倍工作压力（100 kPa）范围内，均匀选取 9个工作压力值作为自变量，输入COMSOL软件作为滴头进口压力，通过仿真计算出滴头出口流量Q作为因变量，利用MATLAB进行最小二乘法计算，建立基于乘幂函数形式的流量与压力关系，得到回归系数Kd和x。

1.1.3 边界条件

滴头流道进水口设为工作压力，出口设为当地大气压，计算出口流速。初始状态设置为滴头内充满水，滴头以外为空气，空气压力为大气压[7]。本文采用精度高、计量小的标准壁面函数，减小梯形滴头流道的壁面对紊流的影响[21-22]。

1.2 遗传算法原理

与传统的优化算法相比，遗传算法生成初始群体开始搜索，按照基因的表达方式，目标函数值转换得到适应数值的信息，而不需要借助其他辅助信息以及参数。遗传算法有 3个基本操作：选择算子、交叉算子和变异算子，各个算子之间即相互配合又相互竞争[23]。遗传算法作为一种全局优化算法，相对于粒子群算法、蚁群算法和鱼群算法等群智能算法，其基本原理简单易懂，初始条件少，广泛应用于不同领域。本文利用MATLAB自带的遗传算法工具箱进行求解。

1.3 COMSOL与MATLAB联合仿真在滴灌灌水器流道优化中应用

COMSOL（COMSOL Multiphysics）是多物理场仿真软件，可用于温度、电磁、流体等多物理场之间的相互耦合用。 COMSOL中包含livelink for MATLAB模块，能够实现与MATLAB软件之间数据的相互传递、相互交流，这样可以利用 MATLAB 及其工具箱进行预处理、模型设定和后处理，进行多物理场模型仿真和遗传算法优化[24]。

COMSOL与MATLAB联合仿真优化滴头流道结构流程是，首先运行MATLAB遗传算法，生成设计变量、设定遗传优化的主要参数，然后在 COMSOL中完成滴头流道结构的参数化建模与计算，最后使用 MATLAB读取 COMSOL仿真结果，计算目标函数，完成遗传算法寻优化。COMSOL与MATLAB两者之间流转交换步骤如下：

1）运行 MATLAB遗传算法，生成流道转角θ、齿高h、齿间距l、齿参差值j和流道单元数n设计变量。

2）将设计变量和已知变量输入COMSOL，进行滴头流道结构的参数化建模与仿真计算。

3）将仿真计算结果传给MATLAB，拟合出Q～H公式。

4）设定遗传算法中选择、交叉、变异参数，开始计算目标函数值。

5）判断是否满足收敛条件，如果是，转向步骤6）；否则，转向步骤1），生成下一代设计变量。

6）求出最优解，计算结束。

1.4 线性回归分析原理

回归分析（Regression analysis）是确定 2种或 2种以上变量间相互依赖定量关系的一种统计分析方法。线性回归分析是最为常用的方法之一，其目的是在因变量和一个或多个自变量之间建立一种关系。该方法可用于因素分析，统计预测，调整因素等，通过求解标准化回归系数，可以分析自变量对因变量的影响程度[25]。求解过程包括多重共线性检验和计算标准化回归系数。

方差膨胀系数（Variance Inflation Factor，VIF）是衡量多元线性回归模型中多重共线性严重程度的一种度量。它表示回归系数估计量的方差与假设自变量间不线性相关时方差相比的比值。当出现严重共线性问题时，会导致分析结果不准确，因而需要及时进行处理。VIF计算如式（4）所示。

式中VIF为方差膨胀系数；Ri为自变量Xi对其余自变量作回归分析的负相关系数。VIF＞5说明存在共线性问题，VIF＞10说明存在严重的多重共线性问题，模型构建效果不理想，需要进行处理。

当分析通过多重共线性检验后，需要计算标准化回归系数，用于比较自变量对因变量的影响程度。标准化回归系数绝对值越大说明该自变量对因变量的影响越大。若回归方程的形式如式（5）所示。

式中Y是估计值；m为变量个数，取5；多项式系数bj是非标准化系数，通过最小二乘法求得。标准化回归系数为

式中Beta为标准化回归系数；σj为Xj的标准差；σY为Y的标准差。

1.5 数值模拟

本文利用 COMSOL软件建立梯形迷宫滴头流道模型，基于标准k-ε湍流模型进行仿真，计算中对梯形滴头流道划分网格。梯形流道结构壁薄且有较多转角，在对流道划分网格时，这些结构对网格质量的影响十分显著。为了避免转角结构给网格划分带来困难，采用平面计算模型来研究流道的水力特性，进行平面模型网格划分[22]。采用的网格大小为0.01～l/20 mm（l为齿间距），因为过密划分网格对于提高计算精度并不明显，还会增加计算时间。本文采用渐变方式划分网格，对于规则、流动变化缓慢的区域，采用较稀疏的网格；对于不规则、流动变化大的区域采用细密网格，疏密网格间平滑过渡，滴头进口设置为100 kPa工作压力。

图2 迷宫流道的网格划分Fig.2 Grid generation of labyrinth channel

1.6 试验方法

为了验证联合仿真计算方法的可行性，评价梯形迷宫滴头流道灌水器实际的工作性能，利用CNC精雕机制作亚克力材料滴头测试样本。按照SL/T67.1—94规范要求，在0.5～1.5倍工作压力（100 kPa）范围内，排列25个滴头按流量由小到大排列编号，取第 3、12、13、23号 4个灌水器为试样[26-27]。由小到大调节滴头的工作压力，在测试压力范围内均匀分布 9个压力点，用量筒测量4个灌水器每一个压力点的出水量，时间不少于3 min，试验重复 3 次，3次所测水量之差不得大于2%，取平均值计算流量，进而得到试样灌水器的压力与流量关系曲线。将试样灌水器每一组压力下的平均流量进行回归，绘制灌水器压力-流量关系曲线。

2 结果与讨论

2.1 优化结果与验证

在COMSOL建模基础上，利用MATLAB遗传算法工具箱进行优化，开展梯形迷宫滴头流道优化联合仿真计算。遗传算法参数选择如下：初始种群规模为 50，遗传终止代数MAXGEN= 50，选择算子采用赌轮盘方式，选择概率为1/3；交叉算子采用两点交叉算子，交叉概率为 0.75；变异算子采用高斯变异，变异概率为 0.02。灌水器的结构参数优化结果如表2所示。

表2 灌水器结构参数优化结果Table 2 Optimization results of emitter structure parameters

根据表2，通过回归分析得到灌水器流量与压力关系为Q=0.466 9H0.4999，相关系数R2为0.99，拟合较好。根据试验结果绘制压力-流量关系曲线如图3所示，由实测数据得到滴头试样流量与压力的函数关系为Q=0.332 3H0.5576，R2= 0.968。对比仿真优化结果，在常压工作压力下，实测平均流量普遍偏小。利用SPSS软件，对仿真优化结果与试样实测结果进行相关性分析，相关性系数为 0.994，根据显著性检验方法计算得到P值为0.000 1，小于 0.001，表明结果有较强相关性。根据GB/T 17187—2009规定，滴头流量模拟计算值与实测值之间的平均误差为6.1%，小于7%，设计的滴头满足国标要求[28-29]。

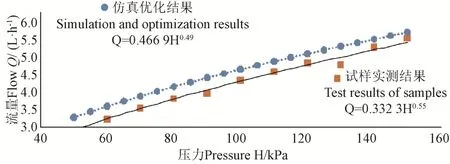
图3 优化结果与实测结果压力-流量曲线对比Fig.3 Comparison of pressure - flow curve between optimized results and measured results

2.2 滴头流道流速

在100 kPa工作条件下，优化参数的梯形迷宫流道灌水器流道的流速矢量分布和速度局部放大图如图4所示。从滴头流道流速分布图可知，各单元之间流速分布一致。根据滴头流道速度局部放大图，可以把梯形滴头流道内部分为3个区域：低流速区域A，处于齿道转角处，速度0.1～1.2 m/s；高流速区域B，处于轴心位置，速度2.8～3.8 m/s；中流速区域C，处于A、B区域之间的过渡区域，速度1.5～2.5 m/s。由低流速区域形状可知，梯形齿尖已经趋近于三角形。基于梯形迷宫滴头流道建立优化模型，得到趋于三角形迷宫滴头流道优化结果，可见三角形滴头相比梯形滴头优势明显[18,30]。

图4 滴头流道流速分布Fig.4 Velocity distribution in emitter channel

从流道内的流速分布图可知，流道进口段流速较低，是长流道滴头容易堵塞位置，与试验研究较为符合[31]。由图4可知，齿道转角部位A区域流速近似为0，该区域流速慢，颗粒易发生沉积，从定性角度来说，更易发生堵塞。以单个齿道为例，A区域面积占截面面积75.1%，从灌水器流道的结构设计出发，下一步可将滴头流道水力性能与抗堵性能作为优化目标，将流道形式设计改为圆弧形边壁，减小低流速区域面积，从而提高灌水器的抗堵塞性能，优化流道设计。

2.3 滴头流道压力

最优方案的梯形迷宫流道灌水器流道压力分布如图5所示，由于整个流道为全封闭状态，没有与外界的能量交换，流道内部流体流动过程中产生了沿程水头损失和局部水头损失，压力由进口到出口逐级减小，从100 kPa下降为 0，13个单元中每个单元段水头损失大约为7.7 kPa，压降基本相同，压力沿流道长度呈线性变化。

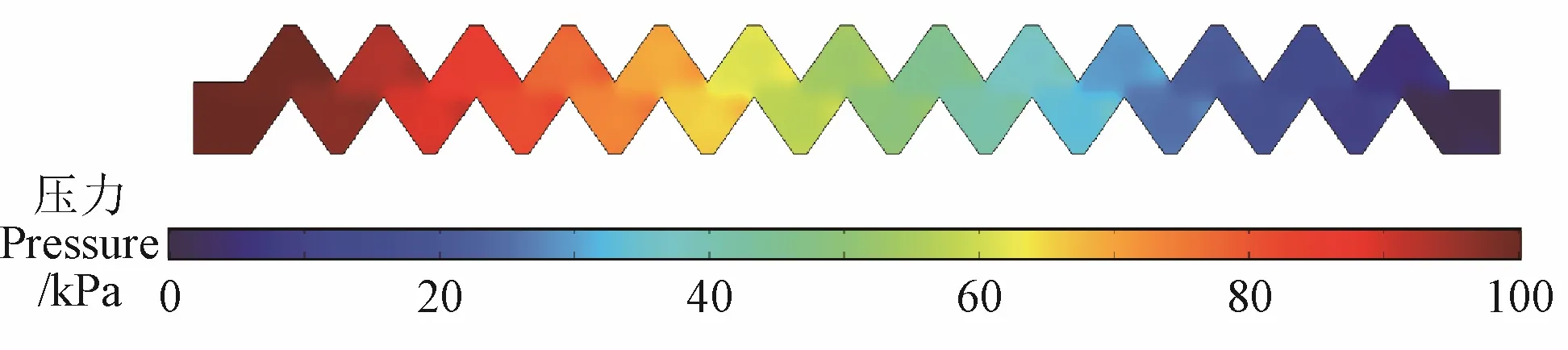
图5 滴头流道压力分布Fig.5 Pressure distribution in emitter channel

2.4 流道结构参数对滴头水力性能的影响

为分析流道转角、齿高、齿间距、单元数、齿参差值5个设计变量对流态指数x的影响，以仿真优化过程中历代遗传算法计算结果数据为基础，利用SPSS软件进行线性回归分析，结果如表3所示。

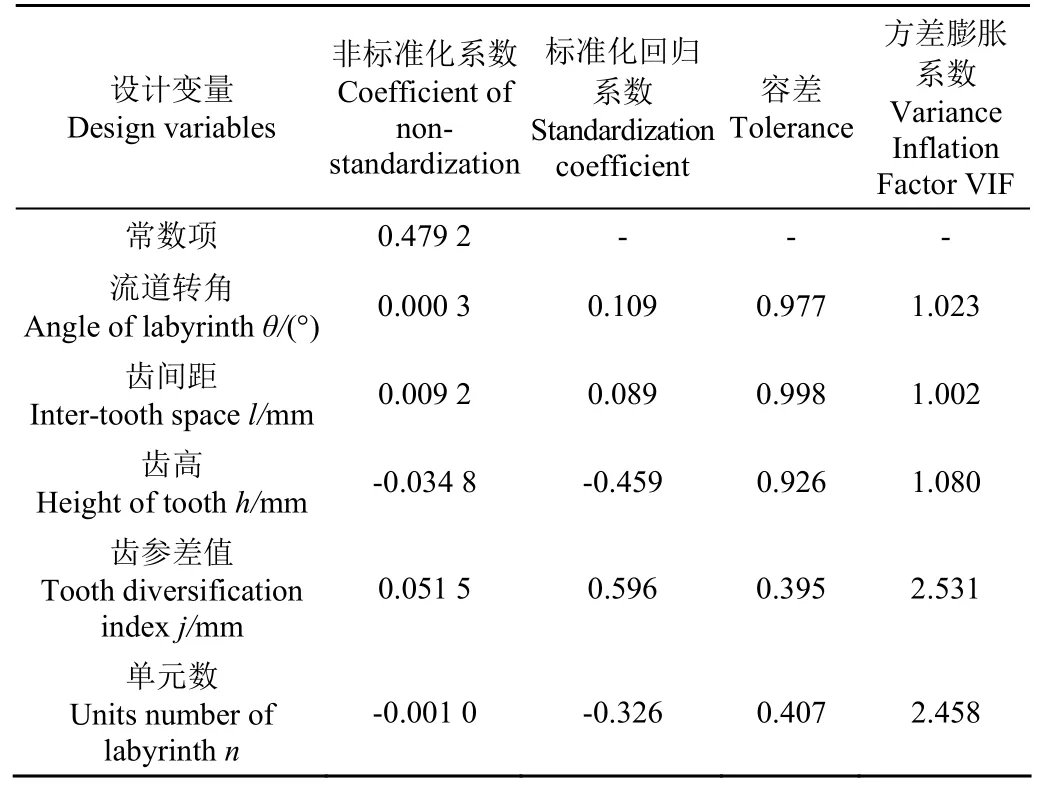
表3 流道结构参数逐步回归分析结果Table 3 Results of stepwise regression analysis of flow channel structure parameters

由表3得到5个变量与流态指数之间的多元线性回归数学模型为

从表3可知，最大的VIF为2.531＜5，说明5个变量不存在共线性问题，说明此模型是可靠的。该线形模型的相关系数R2=0.914，显著性P值为0.001，说明5个变量与流态指数之间线性关系很显著。通过比较5个设计变量标准化回归系数，得到设计变量对流态指数x影响程度由大到小的排序为：齿参差值、齿高、单元数、流道转角、齿间距。齿参差值、齿高 2个参数对流态系数大小起主要影响作用。齿参差值、流道转角、齿间距 3个参数标准化回归系数（Beta）为正值，说明增加齿道的齿参差值、流道转角大小可以增大流态指数；齿高、单元数2个参数标准化回归系数（Beta）为负值，说明减少齿高、单元数可以增大流态指数。由分析结果可知，100 kPa工作条件下，流道结构参数中的齿参差值对滴头的水力性能影响较大。

3 结 论

本文通过MATLAB与COMSOL联合仿真计算求解出常压下最优梯形迷宫流道灌水器流道结构参数，流道内低流速区域流速达到0.1～1.2 m/s，过流面积占流道截面的 75.1%，有堵塞风险；高流速区域流速达到 2.8～3.8 m/s，中流速区域流速达到1.5～2.5 m/s，流道内压力沿流道长度呈线性变化；仿真结果与实测结果的流量误差为6.1%；得到5个自变量对因变量影响程度由大到小的排序为：齿参差值、齿高、单元数、流道转角、齿间距，建立了流态指数与 5个参数之间的多元线性回归数学模型，具有较好的代表性。

本文研究了常压（100 kPa）工作条件下的流道结构尺寸，未涉及低压、高压条件，研究结论有一定的局限性。以流态指数作为判断滴头水力性能的指标外，还需要对滴头抗堵塞性能做进一步研究。受滴灌系统工程造价、作物品种等因素影响，应该开展不同工作压力、不同流量条件下，灌水器流道结构参数优化研究，为开发新产品、推广应用提供科学依据。