基于动态价格的网约车高峰压力缓解机制研究*
2021-01-19朱俊武
夏 宇 朱俊武 姜 艺,2
(1.扬州大学信息工程学院 扬州 225127)(2.上海交通大学海洋工程国家重点实验室 上海 200240)
1 引言
网约车的出现打破了传统出租车行业的垄断和封闭,人们的出行不再担心出租车绕路拒载现象,乘车地点变得更加自由。网约车以这种更加自由、高效的出行方式受到消费者的喜爱,网约车也逐渐成为人们出行的重要交通方式之一。网约车依赖于平台做匹配和定价,而定价问题则是用户关注的重点,平台的定价是司机与乘客选择平台的重要参考依据。定价问题中包含了高峰期和非高峰期下的不同定价方式。高峰期意味着在一段持续时间内运力紧张,一般呈现出阶段性的特征。高峰期下不同的定价策略将会使得乘客的用车成本大不相同。
目前,大部分平台采取了阶梯型的定价策略及高峰期加价策略。例如滴滴在一些城市将工作日分为4个时段,6:00~10:00为早高峰时期,10:00~17:00为平峰时期,17:00~21:00为晚高峰时期,21:00~6:00为夜间凌晨时段,每个时段采取不同的计价方式,在高峰期会采取加价的方式也增加乘客的用车成本。由于阶梯型定价策略,将会使得乘客在同一时间的基础用车成本相差不大,而加价方式会使得部分乘客产生心理落差,对平台满意度下降。提高乘客用车成本在一定程度上可以提高司机的报酬,但由于平台收取高额服务费等原因,使得部分兼职司机的收入达不到预期,导致这部分兼职司机对平台满意度不高,没有动力为平台提供运力。
因此,如何提高高峰期的订单成交数量,提高用户的满意度,为平台缓解高峰期运力压力,是一个具有实际意义的科学问题。
本文通过构建平台在运力紧张时期受价格因素影响的乘车需求和运力供应函数,推导出平台在运力紧张时期的最优价格函数。利用最优价格函数,增加在线司机数量,向平台提供更多运力,减少价格敏感乘客的订单,使得平台在运力紧张时期的乘车需求和运力供应能力尽可能保持平衡。平台中司机可分为全职司机和兼职司机。全职司机可以一直为平台提供运力。而兼职司机由于各种原因,为平台提供运力的时间远少于全职司机。通过动态定价策略,在运力紧张时期提高司机的收入,吸引全职司机和兼职司机增加在线时间,提高司机为平台提供的运力。同时,在运力紧张时期,在保证基础分成系数的基础上,平台给司机的分成系数随运力与订单情况变化,运力越紧张,分成越高。
同样,乘客可以分为价格不敏感乘客和价格敏感的乘客。价格不敏感乘客不在意单次服务价格而价格敏感的乘客在价格超过预期时会放弃提交订单。通过动态定价策略,在运力紧张时期提高用车成本,减少价格敏感乘客在运力紧张时期提交的订单量,将运力分配给价格不敏感乘客,优先满足价格不敏感乘客的需求。
本文针对上述问题,构建了网约车动态定价模型,利用乘车需求和运力供应函数推导求解出网约车供需平衡状态下的最优价格函数,设计算法进行分析并对价格函数进行了模拟实验,为网约车平台在高峰期缓解运力压力问题提供参考。
2 相关工作
关于动态定价方面,Lu等[1]提出了一种销售价格为静态决策变量,补货率为动态决策变量的联合混合策略,说明了不同系统参数对联合最优动态策略和最大总利润的影响。Fellows N T[2]对汽车共享进行的最保守的估计,净收益也与主要道路方案产生的收益相当。Feng[3]研究了质量和数量同时恶化的易腐产品的动态定价和质量投资的最优补货模型,提出了一种以单位时间总利润最大化为目标的动态优化模型。Liteng Zha[4]用一个双层规划框架来研究峰时定价的影响,与静态定价相比,平台和司机普遍享有更高的收入,而客户可能会在高峰时期体验变得更糟。Gérard P.Cachon[5]认为随着劳动力变得更加昂贵,供应商和消费者可以通过峰时价格受益,所有利益相关者都可以从使用一个具有自我调度能力的平台上的峰时定价中受益。Qi Luo[6]利用连续时间连续空间方法研究按需拼车中的动态定价问题,用带群间转移的多人口交通流来描述交通供给的动态模型,为解决拼车及类似匹配市场中复杂的时空定价问题提供了宏观视角。Guda H[7]分析了按需市场中的平台策略并提出即使在供过于求的地区峰时价格也可以发挥作用。Siddhartha Banerjee[8]建立了排队论经济模型来研究最优平台定价问题,提出在任何动态定价策略下的性能都不能超过在最优静态定价策略下的性能。谢莹[9]从复杂问题情景下网约车平台、司机和乘客的利益诉求和行为特征进行深入分析,提出网约车最优里程价随巡游出租车里程价增加而增加,随收取的“回扣”增加而减少。李豪[10]建立以舱位开放和价格变化为决策变量的多周期动态规划模型,得出实行动态舱位控制策略可缓解乘客策略行为对航空公司期望收益的影响,供应水平越高或乘客策略程度越大,其缓解策略行为的效果越明显。赵道致[11]针对网约车和出租车的出行服务竞争,分析了网约车服务等待时间对消费者剩余的影响以及参数对两种服务共存条件的影响。孙中苗[12]针对乘车需求波动导致不同供需状态下的网约车平台定价问题,运用最优控制方法,以平台期望收益最大化为目标,构建乘运供应能力下的平台动态定价模型,探讨了平台服务质量和市场乘车需求变化系数对最优价格和期望收益的影响。Bai[13]、Hu[14]和Taylor[15],运用排队论对网约车平台系统的供需匹配做研究。关于网约车定价方面的优化模型,初始研究的优化目标主要包括最小化运营成本[16]、最大化收入[17]等。
总地来说,现有工作采取的定价策略时固定的定价规则,较少使用动态定价策略,忽略平台不同时间段下乘客需求和司机运力供应之间的关系,较少描述平台订单量及价格随乘客需求与运力供应变化之间的关系,缺少考虑如何缓解平台高峰期的运力压力。因此,本文基于高峰时期下的平台特点,考虑该时期下乘车需求和运力供应的关系,构建动态价格函数模型。利用动态定价策略,在一定程度上缓解平台高峰期运力压力,为网约车平台在高峰期的定价决策提供参考。
3 问题模型与机制设计
3.1 问题模型
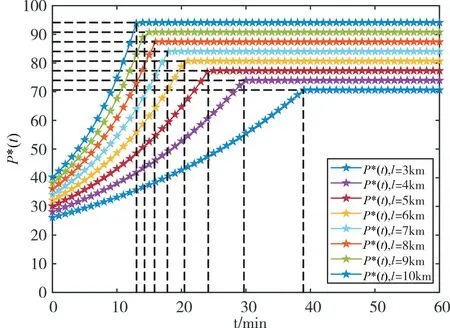
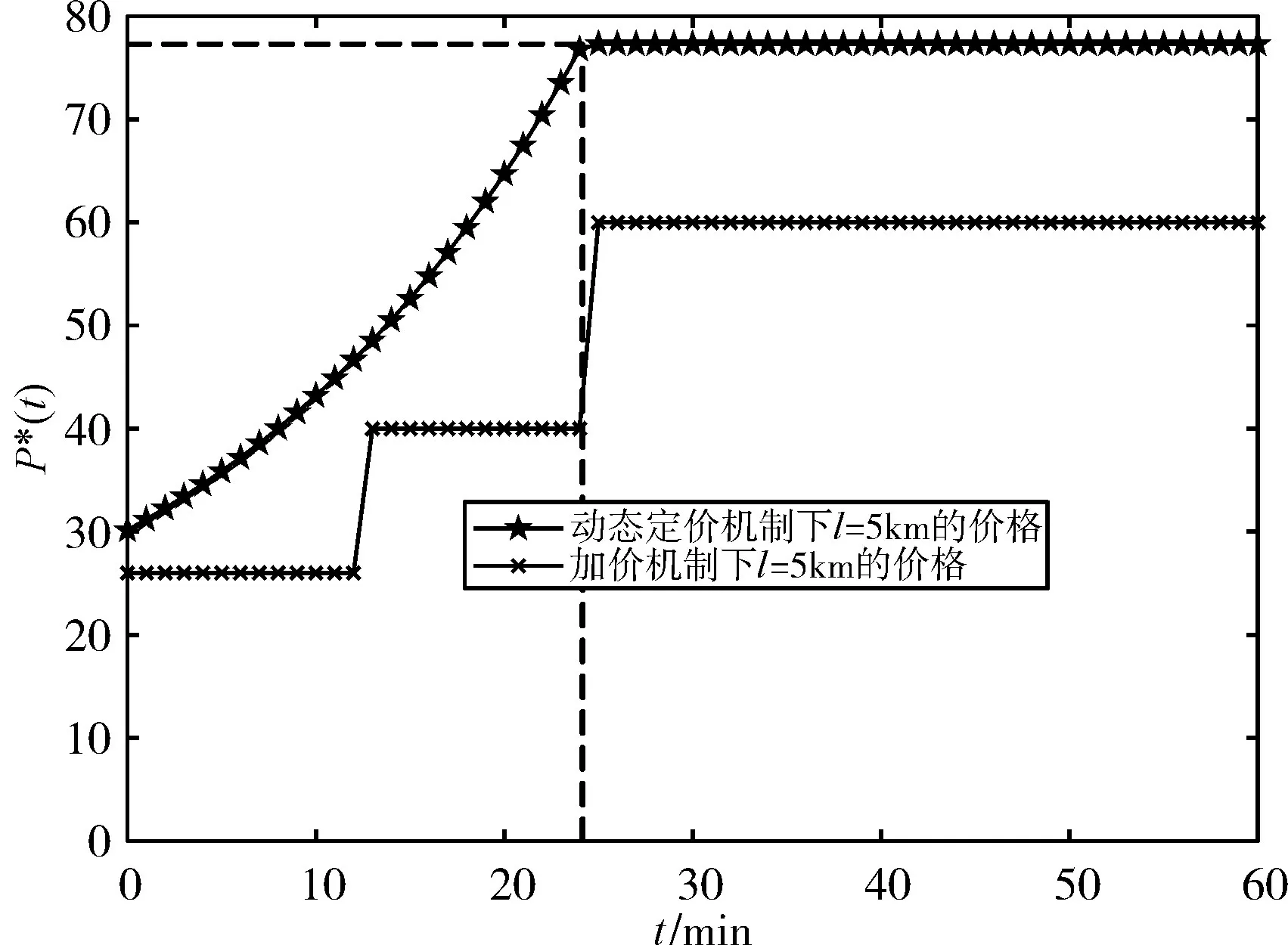
假定网约车市场由网约车平台、司机、乘客三部分组成。针对网约车平台,乘客不取消订单,司机不拒接订单。假定相同里程订单单价用车成本相同,在时间段[0,T]内,平台运力紧张,在t时刻,平台收到的订单数量为D(t),而平台在t时刻的运力为S(t),平台基于t时刻运力紧张程度预计向乘客收取P(t),预计向提供出行服务的司机支付W(t)。由于[0,T]时刻为运力紧张时期,所以平台运力不能满足订单需求(S(t) 假设单次乘车价格由价格函数P决定,r为平台给司机的分成系数,并且0 平台受t时刻价格影响的乘车需求为D(P,t)=deatl-αP(t),其中:a>0,a是一个常数,表示乘客订单需求的受时间t和里程l影响的变化系数[18~19],l代表订单行驶里程,α表示网约车平台的价格敏感系数[18~19],d表示平台在0时刻的订单需求量,d≫0。在运力紧张时期,订单需求随时间t的变化而变化,并且受t时刻价格的影响。用指数型时变需求函数描述了网约车平台乘车需求的波动变化。市场乘车需求增加与现实中上下班高峰期、雨雪天气以及大型活动结束后的一段时间内打车需求逐渐增加是一致的。 考虑运力供应能力与司机收入变化的相关程度[14],假设平台在t时刻的运力供应力为S(P,t)=sW(t)-βl,s表示网约车平台运力供应能力的价格敏感系数。β代表司机对行驶距离的敏感程度。W(t)为平台预计每单支付给司机的报酬且W(t)=r P(t),Ŝ表示平台最大运力供应能力,S(P,t)≤̂。当司机的每单收入W(t)越低时,司机为平台提供的运力就越少,这与网约车平台的实际运营是一致的[14]。 在t时刻,乘客向平台发送订单,请求服务,平台此时计算(t)=D(t)-S(t),当(t)≥0时,t时刻运力匮乏;当(t)<θ时,t时刻运力充足(在本文中,θ设置为0)。假设在[0,T]时间内为运力紧张时间段,那么在[0,T]时间内,平台将采取动态定价策略,并且司机分成系数和乘客需求是单调上升的。价格不敏感的乘客,不在意单次服务价格的上涨,只希望能尽快被分配到司机;价格敏感的乘客在价格超过预期时会放弃提交订单。全职司机对日均收入敏感,是平台日常运营的重要组成部分,保证这部分司机的留存可以保证非高峰期的运力充足。兼职司机对单次服务收入敏感,在运力紧张时,通过提高订单价格,提高司机分成,增加司机单次服务收入,兼职司机可以提供相当一部分的运力来缓解平台运力压力。 [0,T]时间为运力紧张时期,平台按照就近原则快速匹配,将订单分配给距离乘客最近的司机。订单需求随时间的推移不断上升,而运力也会由于动态定价策略导致的单次服务价格上升而逐步上升,但平台运力存在极限,当运力达到极限时,会产生延误订单,订单延误会产生时间成本。平台中对价格不敏感的乘客,考虑到运力与订单数量的比例,平台采取动态定价策略,乘客需要支付给平台的价格P(t)较运力充足时会有所上升,这部分乘客不会取消订单。而对价格敏感的乘客,由于动态定价策略下的价格调控会导致这部分乘客放弃在时刻t提交订单需求,此时会产生延误成本h,若乘客在t'时刻时且(t')>θ时提交需求订单,平台将会对延误成本h进行补贴,此措施将会转移运力匮乏时的平台压力,并通过补偿乘客时间成本来保证乘客的留存。在运力紧张时,利用价格调控策略来满足价格不敏感乘客的需求,通过一定的补偿手段,延后价格敏感乘客的需求,将t时刻的部分订单进行延后处理,减少了在运力紧张时期的订单需求,在一定程度上缓解平台运力紧张时的订单压力。 司机每单收入受到动态定价策略和分成系数r的影响。对于全职司机来说,每单收入的增加会提高自己的日均收入,所以在运力紧张时,全职司机会一直提供自己的运力。对于兼职司机来说,由于每单收入的增加,运力紧张时期,他们会成为平台的兼职司机为平台提供运力。通过动态调价策略,提高单次服务收入,并增加司机的分成系数,鼓励兼职司机的加入可以增加平台运力,提高平台承载力,满足更多的订单需求,在一定程度上减少延误订单,并使得高峰期时间段缩短。平台的最终分成系数r*由平台运力情况̇(t)决定,当运力紧张时,司机的单次服务收入将会得到提高。 为了利用动态价格调控方式吸引更多的兼职司机在运力紧张时期提供运力,减少价格敏感用户在运力紧张时期的订单,使得运力在一定时间内不断增加,满足乘客订单需求,本节提出一种动态定价算法。 假设在[0,T]时间内,̇(t)≥0,该时间段为运力紧张状态,此时,u(t)≥0,本文将价格P(t)作为控制变量,基于平台在t时刻根据价格的运力供应和乘车需求,构建延误订单量的状态方程: 所以在t时刻平台累计延误订单量为 Algorithm 1:动态定价算法 Input:D(t);S(t);d;α;β;a;l;s;r;L;t;T;Ŝ Output:P(t);W(t);W*(t) 1 for t=t+1 and t≤T to 4 此时处于运力紧张状态,调用运力紧张时的动态价格 7 if 0 8P(t)=deatl+βl α+sr 9 W(t)=rP(t) 10W*(t)=r*P(t) 11 end 12 else if t* 13P(t)= 14W(t)=rP(t) 15W*(t)=r*P(t) 16 end 17 end 18 end 19 returnP(t);W(t);W*(t) 在运力紧张时期[0,T]内,由于乘车需求的增加,平台运力供应能力无法及时满足乘客乘车需求订单量,所以t时刻平台实际可以满足的乘客乘车订单量为Min(D(P,t),S(P,t))=S(P,t)。 本文假设平台的动态定价和动态分成系数策略可吸引的兼职司机数量存在上限。假设在[0,t*]时间内,由于每单收入的增加,不断有兼职司机加入平台。这个时间段,平台通过吸引兼职司机加入,提高平台最大运力,尽可能满足乘客的订单需求;在t*时刻,平台运力达到极限̂,价格措施不能吸引更多的兼职司机加入;因此,在[t*,T]时间内,不再有兼职司机加入平台,平台保持定价策略来维持平台最大运力̂,用最大运力来满足乘客的订单需求。 定理1:假设平台在[0,t*]内不存在运力上限,那么平台的最优定价为 证明:在平台服务时间[0,t*]内,运力供应低于乘车订单需求,即u(t)≥0,由于u(0)=0,所以只需u'(t)≥0,结合运力供应S(P,t)和乘车需求D(P,t),令D(P,t)≥S(P,t),得: 由上式可知: 由定理1可知在运力紧张时期[0,t*]内最优定价,将最优定价代入S(P,t)和D(P,t): 在时间[0,t*]内,市场乘车需求增加,由于在时间[0,t*]内,平台提供的运力没有上限,为了增加单位时间内订单成交量,最优价格函数P*(t)将最大程度上激励兼职司机加入平台,提高平台单位时间内的运力,可以使得S*(t)=D*(t)。而最优价格函数P*(t)将随着时间的推移而不断增长,持续吸引兼职司机为平台提供运力。最优价格函数使得平台在运力紧张时期达到了供需平衡状态,减少了订单延误。此时,平台最优价格、运力供应和乘车需求随着时间t和里程l的变化而变化。 定理2:假设平台在[t*,T]内存在运力上限 证明:在[t*,T]时间内,由于不再有兼职司机加入平台,此时存在运力供应上限Ŝ,平台获得市场最大运力能力Ŝ,并且之后平台一直维持最大运力,此时S(P,t)max=srP(t)-βl=Ŝ,可得:时,平台最优定价为 由式(5)可以得到S*(t*)=Ŝ,因此可得: 在时间[t*,T]内,市场乘车需求继续增加,但是平台提供的运力存在上限。在时间[0,t*]内,最优价格函数单调递增,在t*时刻达到顶峰,此时平台已提供最大运力̂,平台无法通过提高司机收入激励更多的司机加入平台来提供运力。在现实生活中,在高峰堵车期,由于平台乘运能力的上限,乘客会面临更长时间的等待。这与本文的描述是一致的。 同时,本文考虑到司机分成系数,当进行司机预估收入W(t)的计算时,r采用固定的分成系数,而最终结算时的W(t)采用动态分成系数r*进行计算。采用固定分成系数的P*(t)小于采用动态分成系数的P*(t)。 其中L是一个常数且0 为了验证本文提出的机制的有效性,本节模拟一个场景。假设在时间段[0,60]内为平台运力紧张时期(即T=60),假设平台初期运力d为100,平台运力上限̂为180。计算司机预估收入W(t)时采用固定分成系数r=0.85。而司机实际收入W*(t)采用动态分成系数r*。最终的模拟结果如图1所示。 网约车平台的最优价格P*(t)随时间t和里程l的变化曲线如图1所示。最优价格P*(t)在[0,t*]时间内是一个单调增函数,伴随着时间的变化而增加;而在[t*,T]时间内,最优价格P*(t)维持在一个稳定的数值,不再随时间的变化而变化。相同里程的订单保持相同的用车成本。随着订单里程的增加,乘客的用车成本也在不断上升,到达价格顶峰的时间也在不断缩短。这是由于里程越长的订单所花费的时间越长,单位时间内订单完成量就会减少,运力会被一直占用,所以到达运力上限的时间随着订单里程的增加而减少。 图1 里程3km≤l≤10km时的最优动态价格 动态定价的价格函数和采取阶段定价加价模式的对比如图2所示。动态定价方式的价格在一定时间内单调上升,并在一个时间点后稳定。而阶段定价方式的价格在一定时间内时相同的。采取阶段定价方式的价格低于动态定价方式的价格。但阶段定价方式不能反映乘车需求与运力供应之间的实时关系,阶段定价方式的乘客在相同时间内乘客的用车成本相同。 图2 里程l=5km时动态定价和阶段定价的价格 网约车平台的运力供应和运力需求量如图3所示。运力在[0,t*]内没有达到平台运力供应上限,在最优价格P*(t)的调控下,不断有新的运力加入平台,来满足上升的订单需求,在[0,t*]时间内运力和需求保持平衡。在[t*,T]时间内,由于运力不再上升,将会造成乘客订单的延误。这表明,伴随着时间t和里程l变化的最优动态价格可以影响乘运供应能力。 图3 里程l=5km时运力供应与需求变化 从图4中可以看出,采取动态分成系数下的司机收入大于采用固定分成系数下的司机收入,收入的增加在一定程度上可以增加兼职司机加入平台的动机,吸引更多的兼职司机加入,提高平台的运力,缓解平台运力紧张时期的运力压力。 图4 里程l=5km时的动态分成和固定分成 总地来说,通过动态价格调控机制,不断吸引兼职司机的加入,同时减少价格敏感用户的订单,在一定程度上可以缓解平台在高峰期的运力压力。本文模拟受限于司机数量的上限,根据模拟结果,如果平台中存在足够多的兼职司机,通过动态价格机制,可以在运力紧张时期尽可能多地满足乘客订单需求,提高订单成交量,平台效用同样获得上升,用户满意度也将有所提高。 网约车平台高峰期的运力紧张状况是一个十分显著的问题,如何平衡高峰期供需压力是研究的重点。目前,大部分平台采取的是阶段价格函数和加价机制的组合,这种方式不能反映供需关系的实时变化。本文通过构建网约车动态定价模型,利用模型推导求解出网约车供需平衡下的最优价格函数以及乘车需求与运力供应的变化曲线。实验表明,通过最优价格函数,在运力紧张时期吸引兼职司机的加入,减少价格敏感乘客的订单,在一定时间内可以保证乘车需求和运力供应一定程度上的平衡,增加单位时间内订单完成量,最终在一定程度上缓解了网约车平台在高峰期的运力压力问题,为网约车平台在高峰期采取什么方式缓解运力压力问题提供参考。 但是本文主要研究运力紧张时期的定价机制,而平台在运营过程中还存在着运力充足时期。在运力充足时期,如何减少空载司机的数量,降低平台运营成本,是接下来需要解决的一个问题。在下一步工作中,还需要考虑到平台之间的竞争带来的影响。同时,如何计算平台的效用和社会福利也是接下来需要解决的问题。3.2 网约车高峰压力缓解机制
4 算法设计和分析

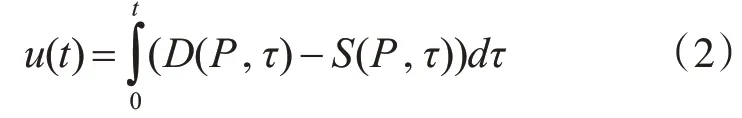


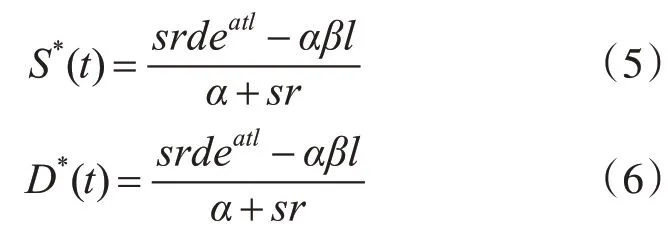

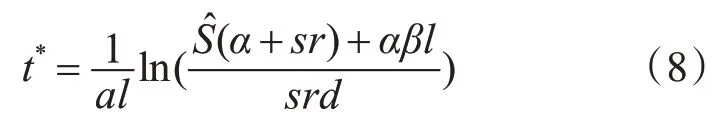
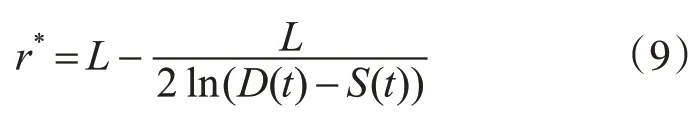
5 实验


6 结语
