考虑失效机理的舰船机电设备加速可靠性增长模型研究∗
2021-01-19熊波波窦晓彤
吴 昊 熊波波 窦晓彤
(1.中国舰船研究院 北京 100192)(2.广州广电计量检测股份有限公司 广州 510656)
1 引言
随着技术的革新和进步,舰船信息电子等机电设备的不断发展,人们对产品的可靠性要求越来越高。一方面机电设备产品的固有可靠性水平不断提高,另一方面,人们对产品的可靠性要求也越来越高。在这种情况下,原有的可靠性增长的方法和模型在实践应用中遇到前所未有的困难和挑战。这些困难和挑战主要集中在:平均故障间隔时间MTBF度量指标日益提高,达到几万小时的数量级,按照传统方法设计的可靠性增长方案和试验周期太长,代价高,难以实施;新型的产品设计理念、系统级的可靠性管理和优化方法以及可靠性试验方法不断提出,但这些方法给出的可以揭示系统可靠性信息和状态的信息却未得到有效利用,由此为提高产品可靠性,需开展可靠性增长工作。
可靠性增长工作贯穿于产品整个寿命周期[1]。由大量实践证明,在工程中,通过可靠性增长试验、分析与管理来提高产品的可靠性,是节省试验时间、减少试验次数和降低研制经费的有效办法。其中加速可靠性增长的理论方法,实际就是参照加速寿命试验的方法,对产品施加比正常应力更严酷的应力,使产品的故障快速暴露,在对故障加以分析,纠正后,通过合理的改进措施,使产品的可靠度有较大幅度的提高,从而实现产品的可靠性快速增长。因此,对加速可靠性增长技术的研究是一项意义深远的任务。
2 传统加速可靠性增长模型
为解决快速实现可靠性增长的问题,加速可靠性增长试验(Accelerated Reliability Growth Test,ARGT)的提出提供了一种新的方法:在保持产品故障机理的前提下,ARGT应用加速的环境应力,使设计和生产中的缺陷以故障的形式提前暴露,从而进一步对故障进行分析,校正,然后可靠性可以实现快速增长。该方法出现于在20世纪90年代,通过对产品施加比正常应力更严酷的应力,以实现产品可靠性快速增长。从2000~2002年,北京强度环境研究所的周源泉[2~7]等发表了一系列的论文,提出借鉴ALT的思路,将加速因子的概念引入可靠性增长试验中,是目前最为系统介绍ARGT的文献。此外,西北工业大学吉国明[8]在其论文也涉及到这个问题,他提出了应力时间双因子影响函数l(s,t)=f(s)*g(t),分别采用Cox’s模型和Duane模型描述应力影响因子和时间影响因子。但是,从文章叙述的角度来说,所提出的模型缺乏可靠的物理意义,并没有深刻的理解比例风险模型的实质,有相当的局限性。
目前,关于加速可靠性增长试验的文献数量有限,而且研究还很不成熟,多只是停留在理论研究的层次。此外,对于加速可靠性增长试验,目前对于加速应力的施加还主要是运用单个应力,单应力水平下的加速可靠性增长试验的提高总有一个限制,超过此限制时将使产品的故障机制发生变化。为了在试验过程中保持产品故障机制不变,应力水平不应设置得太高,以致产品试验的时间的缩短将受到限制。为了进一步提高产品的试验效率,缩短研制周期,下文基于双应力的加速寿命试验艾林模型和增长试验AMSAA模型,对加速可靠性增长试验方法进行了研究。
3 基于双应力条件的加速可靠性增长模型
3.1 双应力加速可靠性增长模型
加速可靠性增长试验是加速试验和可靠性增长试验的统一[9]。一方面利用可靠性增长试验暴露缺陷,并进行修正;另一方面利用加速试验缩短产品的研制周期。这里首先建立可靠性增长模型,本文采用AMSAA增长模型来描述ARGT中产品故障出现的规律。
基于产品的失效间隔时间ti-ti-1(i=1,2,…,n)随机的增加时,故障率严格单调下降,产品处于可靠性增长之中。现在将AMSAA模型写成下面形式:
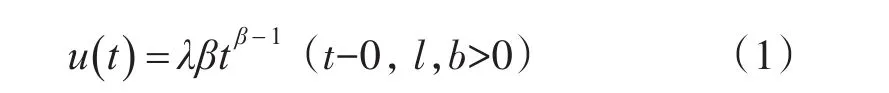
其中:l为强度参数;b为形状参数。
将产品的可靠性水平用MTBF,也就是产品瞬时失效率的倒数,表示为

为了方便利用寿命特征与应力之间的关系,设λ=η-β,此时称η为尺度参数。则上式改写成如下形式:

对于整个加速可靠性增长试验,一方面,它属于可靠性增长试验。而从另一方面来看,它又属于加速寿命试验。因此,在确定完增长模型后,需要确定加速模型。
由于故障强度函数中的尺度参数η表征了时间的概念,因此我们假设η与产品的受试应力S(S代表的是广义应力,本文这里是由两个应力组成)相关,即η=η(S)是加速模型。
对综合应力的加速模型已开展研究[10~12];但当加速模型中考虑多应力后,一个是模型过于复杂,且没有固定的公式;另一个就是考虑多应力的加速模型,其简化和计算较复杂。故这里选择一种考虑双应力的广义艾林加速模型,其中一种应力为温度应力,而另一种为非温度应力,两种应力同时作用。该模型为
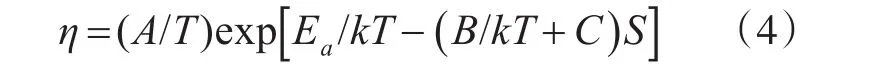
式中:A,B,C为待定常数,Ea为激活能,也为待定常数,k为波尔兹曼常数。
令η’=ηT,再对其两边取对数,可得:
其中:a=lnA,b=Ea/k,c=-C,d=-B/k,Ψ(T)=1/T,Ψ(S)=S。
工程应用中常把η’中的T省略,再令Ψ(S)=lnS,故式(5)再次简化:
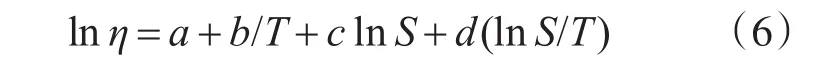
3.2 模型参数估计
3.2.1 增长模型参数估计
设有ki个产品处在多恒定Si(i=1,2,…,m)应力下进行同步可靠性增长试验,且系统的故障时间为0=t0<ti1<…<tij<Ti。每组应力下的累积失效数为 ni,且故障数 N(s,t)=N(t)-N(s),(t>s)服从均值为 EN(t)-EN(s)的泊松分布,在无穷小的区间(t,t+dt)内,发生失效的概率为m(t)dt。考虑到布尔过程的独立增量的性质,可以得到定时截尾数据的似然函数为
式(9)中的参数估计值并非是无偏估计,同时,根据产品的失效机理在试验过程中保持不变,也就是形参β不变。因此,参数得到无偏估计可表示为
此时,当产品定型后,其MTBF的最小二乘估计为
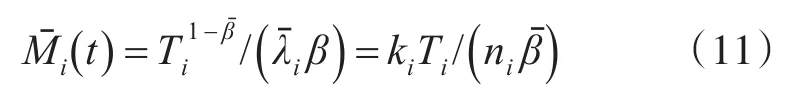
3.2.2 加速模型参数估计
对式(6)可以通过多元回归分析的方法,通过计算可以实现对其参数进行估计。设在试验条件下,可获得n组数据(Ti,Si,Yi),i=1,2,…,n,其中,Ti为温度应力,Si=lnsi为非温度应力,Yi=lnηi为增长模型估计尺度参数,则式(6)可写成:

4 算例及分析
4.1 引言
在本案例中,选用学者周源泉在其文献[6]中应用蒙特卡洛仿真方法模拟某种机电设备的失效数据,其采用单应力形式对产品施加加速应力,并假设每个单应力水平下,得到的故障数据服从非齐次随机过程,且这些数据相互独立,试验中产品的失效机理不变。其模拟获得4组单应力水平下的失效数据,见表1,这些数据可以用来验证本章节提出的方法的可行性。
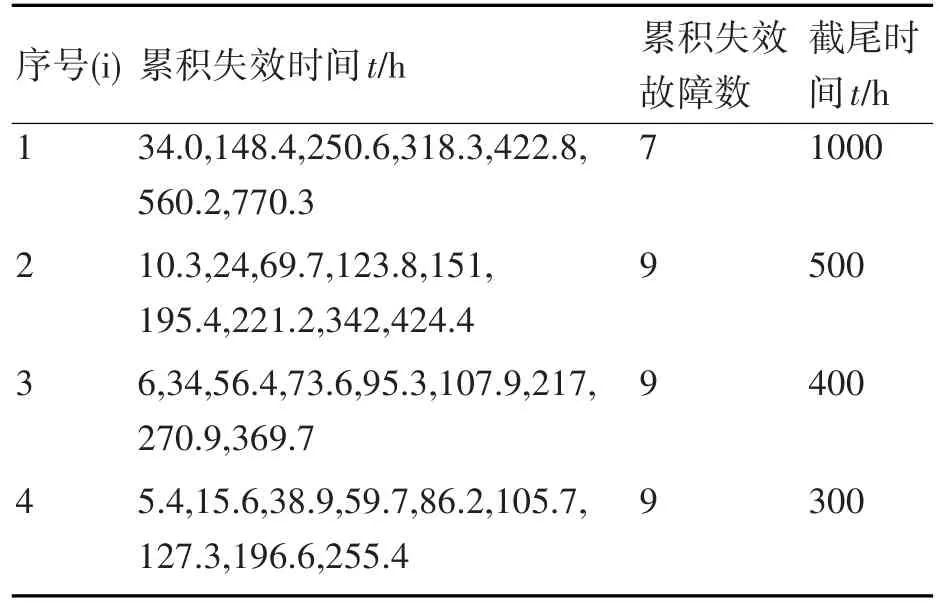
表1 产品模拟的单独累计时间截尾失效数据
在原文中,作者依据对产品的了解,借鉴以往的数据,分析了产品的失效机理,找出了产品的主要敏感应力S进行分析,实际过程中温度应力等其他工作应力对产品的工作也存在影响,这里依据均匀正交试验设计的方法[13],提出产品考虑温度应力的双应力施加的方式,具体见表2,其中每组的样本数均为1个,正常应力下的温度应力T0为298K,非温度主要敏感应力S为1g。
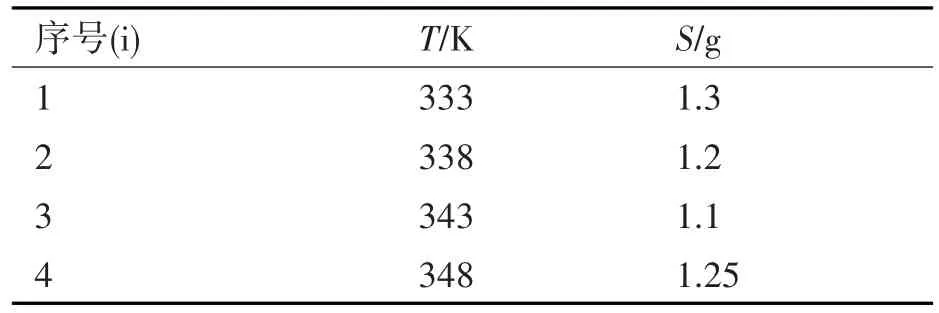
表2 加速双应力施加分布表
4.2 参数估计
由表1和表2中的数据,可以得到各参数的估计值。首先,依据式(10),根据最小二乘法可以得到可靠性增长模型的参数值,见表3。
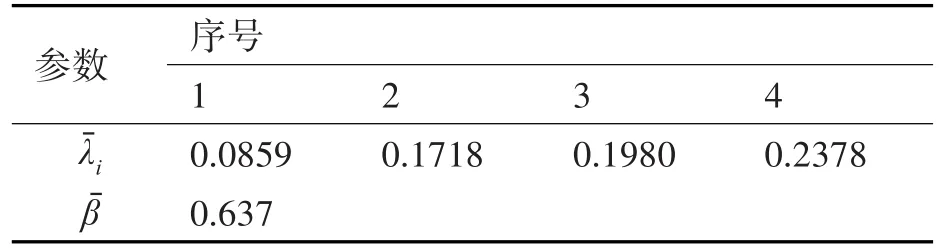
表3 可靠性增长模型参数估计结果
接着,将试验的已知参数Yi,Ti,Si(i=1,2,3,4)值代入式(13)~(15),可以计算出加速模型的参数,具体值见表4。

表4 加速模型参数估计结果
对于加速模型的参数估计,需要对其拟合优度进行检验,判断其是否满足多元回归。这里我们选用如下的公式:
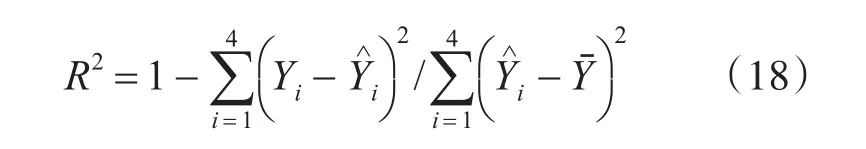
经计算,可得R2≈1,因此该多元回归的拟合度较好,可以进行下一步加速因子的计算和寿命的估计。再次通过式(16),可计算产品的MTBF估计值Mi,以及加速因子Ki0和产品在正常应力下的MTBF值Mi0均可得到,具体值见表5。
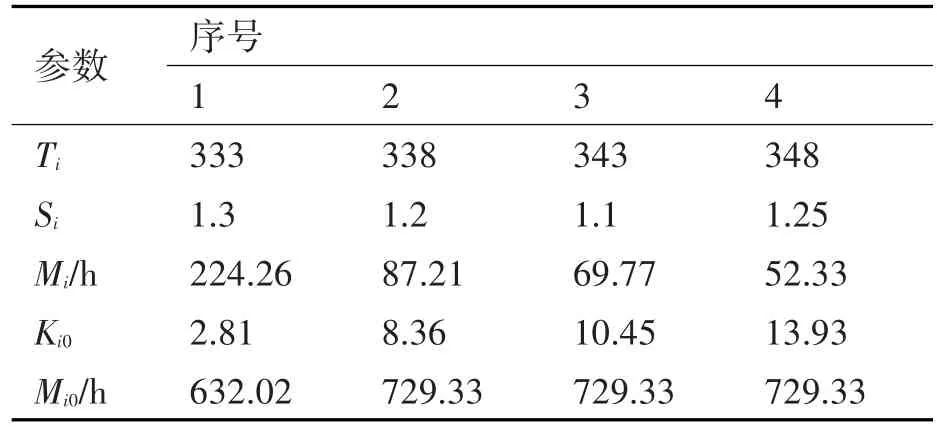
表5 产品特征值计算估计值
4.3 结果分析
表5中的故障数据参数估计,可以通过蒙特卡罗仿真模拟从文献[6]中获得。具体数据见表6。
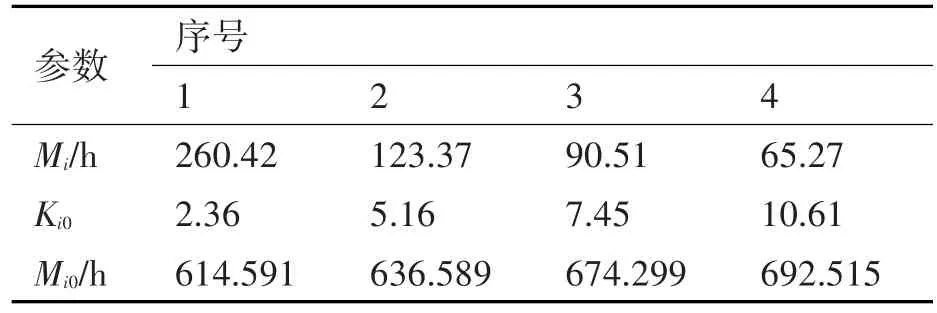
表6 产品寿命特征模拟值
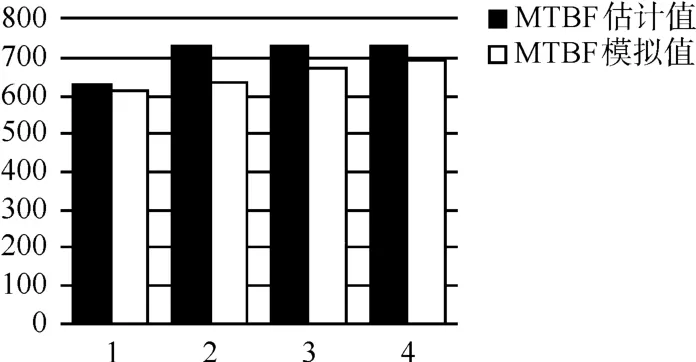
图1 MTBF的估计值和模拟值比较图
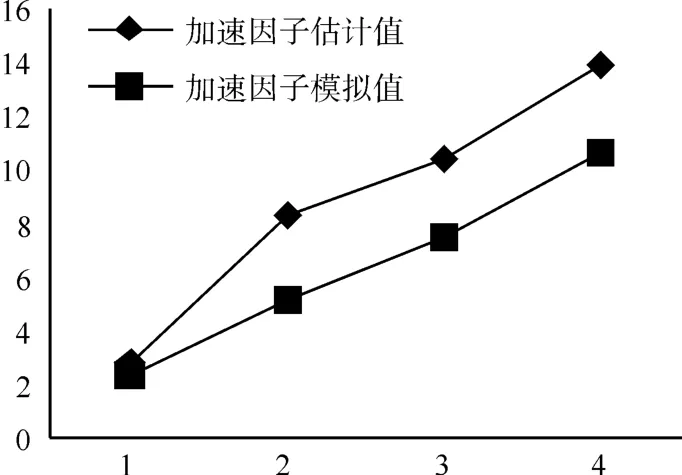
图2 加速因子估计值和模拟值比较图
通过比较表5和表6中的Ki0和Mi0值,具体结果比较显示见图1和图2。通过图1我们可以发现四组加速应力下,产品的MTBF的估计值和模拟值基本相同,证明了本文的模型准确性。图2反映了在对产品施加双应力的条件下,其加速因子一般比对产品施加单应力的时候大,这正好说明了双应力的施加可以大大地改善试验的时间,提高试验效率。
5 结语
本文先分析了现阶段的传统加速可靠性增长模型及方法,得出关于加速可靠性增长的研究还很不成熟,多只是停留在理论研究的层次上,此外,对于加速可靠性增长试验,目前对于加速应力的施加还主要是运用单个应力,在此基础上,为了进一步提高产品的试验效率,缩短研制周期,提出了基于双应力的加速可靠性增长模型方法,包括分别对增长模型和加速模型的分析及参数估计,及对产品寿命估计;最后通过实例对该方法进行了验证分析。
通过本文的研究,有望将加速试验的方法引入到可靠性增长试验中,从而提出一种加速可靠性增长技术研究的模型和方法,进而应用到工程中的实际产品中,使得试验次数得以减少,试验成本降低,试验周期缩短,带来直观的经济效益和社会价值。
