附加视线向量修正的卫星影像区域网平差
2021-01-18张永生赖广陵
伍 洋,张永生,李 凯,于 英,赖广陵
信息工程大学地理空间信息学院,河南 郑州 450001
高分辨率光学卫星影像的高精度几何定位能力是其得到充分利用的关键,也是摄影测量领域一直以来研究的热点。传统有理函数模型(rational function model,RFM)作为一种替代严密几何模型的通用成像模型,以其独立于传感器、形式简单、保密性强等优点,已经成为遥感影像发布的基本几何模型,在实际使用中得到了广泛应用[1]。然而,RFM本质上仍然是对严密几何模型的一种数学拟合,卫星成像过程中姿态和轨道的测量误差会导致采用RFM直接定位存在明显系统误差。
针对这种情况,目前常用的技术手段是在像方或者物方构建系统误差补偿模型,在平差过程中求解模型参数,从而实现对影像几何定位误差的修正与补偿。补偿模型的目的是对影像存在的系统误差进行吸收,根据模型的不同,主要分为:平移模型、平移+比例模型、仿射模型、多项式模型。其中,平移模型具有形式简单、适用性广的特点[1-3];平移+比例模型在平移模型的基础上添加了一个比例系数来吸收姿态漂移造成的误差[4-5];仿射模型目前应用最为广泛,可以获得比平移模型、平移+比例模型更高的补偿精度[6-11]。文献[12—13]在对多种模型进行深入讨论的基础上,还对模型引入的近似条件及误差进行了分析。文献[14—15]对多项式模型的补偿效果进行研究,得到了很好的试验结果,但由于内外方位元素相关性以及模型参数过多,需要大量控制点数据。此外,文献[16]根据薄板平滑样条函数构建误差补偿模型,利用其良好的拟合性和灵活性修正ZY-3影像存在的系统误差。
以上所述方法尽管模型存在差异,补偿效果也不尽相同,但从原理上看,这些模型本质上都是对物方或者像方残差的近似拟合。为避免建模空间单一,模型存在近似的问题,文献[17—18]探讨了利用RFM模型恢复影像严密几何模型的方法,但该方法需要准确的初值,且无法解决线、角元素强相关造成的求解不稳定;文献[19]在分析严密几何成像模型和有理函数模型的基础上,提出了一种适用范围更广的抽象几何成像模型;文献[20—21]提出了一套“恢复-补偿-生成”的策略用于提升影像定位精度,取得了一定的效果,但整个处理过程略显烦琐,必须将需要优化的所有影像处理完成后才能采用区域网平差的方式进行几何定位。尽管有不少方法上的创新成果,但从处理数据类型的角度来看,目前已有的研究都针对测绘卫星数据进行,关于非测绘卫星数据处理的研究成果较少。原因是非测绘卫星影像数据通常并不符合立体测图条件,普遍存在姿态角误差大、影像视场角大、重叠影像交会角小等情况。而传统区域网平差能够有效进行的前提就是立体测图条件良好,这极大地限制了卫星影像的应用率。尽管目前针对单一的弱交会影像定位问题,有一些研究成果[22-24],但其能够有效进行的基础是辅助DEM数据的支持,并且存在高程坐标依赖于所采用的DEM数据精度的技术缺陷。综上所述,针对传统区域网平差有效进行存在的限制条件,有必要发展一种能够扩展影像使用类型的通用系统误差补偿方法。鉴于此,本文提出了一种附加视线向量修正的卫星影像区域网平差方法。该方法从成像光线的视线向量出发,将传统策略从对残差建模变换为对产生系统误差的原因建模,从而规避传统方法受限于窄视场角相机、高精度姿轨观测系统以及良好交会角的限制。
1 传统区域网平差模型的局限性
传统区域网平差方法首先在RFM基础上建立像方或物方的误差补偿模型,然后根据控制点和连接点坐标构建误差方程,最后利用最小二乘方法求解误差补偿参数和连接点物方坐标。在整个区域网平差过程中,关键步骤在于系统误差补偿模型的构建。目前的通用模型是仿射变换模型,仅仅是对窄视场角相机(视场角小于5°)、平台轨道和姿态测量误差比较小(小于2″)的情况下的近似[6]。当参与平差的影像不满足这种近似条件时,采用该方法就不能有效处理。下面对外方位元素误差造成像点在物方空间的坐标移位进行具体分析,阐述传统区域网平差模型的局限性。
卫星成像时刻外方位元素包括3个线元素和3个角元素(俯仰、滚动、偏航),其中以滚动角误差对定位产生的影响最为复杂,如图1所示。

图1 滚动角误差对几何定位影响Fig.1 Influence of roll angle error on geometric positioning
图1中,点O是光学系统中心;C为光学系统在焦平面上的主点;OC为主距f;a、b是CCD两端点;∠AOB为相机视场角;α为半视场角。A′A和C′C的距离之差即表示由滚动角误差引起的地面点偏移在视场中心和边缘的差异。
假设滚动角误差为r,成像时相机侧摆角为c。根据图1所示的几何关系,可以计算得到
A′A=A′C-AC=H·tan(c+α+r)+
f·tanr-H·tan(c+α)
(1)
C′C=(H+f)·tan(c+r)-(H+f)·tanc
(2)
因此,视场中心和边缘的差值Δ可以表示为
Δ=A′A-C′C=H·[tan(c+α+r)+
tanc-tan(c+α)-tan(c+r)]+
f·[tanr+tanc-tan(c+r)]
(3)
由式(3)可以看出,滚动角误差造成的中心点与边缘点的位置偏移值不一致,两者差值与焦距、视场角、滚动角误差以及侧摆角均有关系。当该偏移值足够大时,并不能用一个简单的线性模型对滚动角误差造成的影响进行有效吸收。
目前卫星平台进行立体观测主要有3种模式:多线阵立体模式、宽幅立体模式、机动立体模式[21]。其中,多线阵立体模式采用多视线阵载荷对同一区域成像构成立体;宽幅立体模式采用宽幅相机从异轨上分别对同一地区进行成像,成像过程不进行机动,通过宽覆盖的重叠区域形成立体影像;机动立体模式仅采用平台上的一个线阵载荷,通过姿态快速机动实现对同一地区不同视角的立体观测。为了观察中心视场和边缘视场偏移的差值Δ随滚动角误差的变化情况,选取了几种不同立体观测模式的国产卫星,其相关传感器参数见表1。按照式(3)计算在不同滚动角误差情况下的数值,统计结果见图2。

表1 典型国产光学卫星相关载荷参数
从图2中可以看出,对于幅宽大且侧摆角大的载荷,当滚动角误差比较大时,由滚动角误差引起的中心视场和边缘视场的偏移差异可达到百米量级;对于幅宽小且侧摆角小的载荷,由滚动角误差引起的中心视场和边缘视场的偏移差异相对较小。
传统区域网平差误差补偿模型构建的假设条件是相机视场角较小,姿态角误差较小,此时由滚动角误差引起的中心视场和边缘视场偏移值的差异可以认为是0,用像面平移模型即可表示由滚动角误差造成的影响。然而,当成像条件不满足近似假设时,对残差结果进行建模的传统方法则存在局限性,此时平移模型并不能有效吸收这种影响。
2 附加视线向量修正的卫星影像区域网平差
针对传统误差补偿方法存在的技术短板,本文提出了一种适用范围更广的卫星影像区域网平差模型。该方法的主要思想是:首先利用RFM模型恢复卫星影像成像时的视线向量,再根据视线向量恢复出摄影时刻的虚拟外方位元素,然后对虚拟外方位元素进行误差建模,构建新的观测方程,最后采用最小二乘方法进行求解。其主要流程如图3所示。

图2 滚动角误差引起的中心视场和边缘视场偏移差值Fig.2 The difference of center field of view and edge field of view caused by roll angle error

图3 附加视线向量修正的卫星影像区域网平差算法Fig.3 Satellite imagery block adjustment based on line-of-sight vector rectification
2.1 恢复虚拟外方位元素
对于任意像点p(i,j),给定两个不相等的高程值H1和H2,结合影像的RPC参数文件,可以计算出相应的地面点大地坐标P1(X1,Y1,H1)和P2(X2,Y2,H2),根据两点坐标可以计算出该像元的成像视线向量,如图4所示。
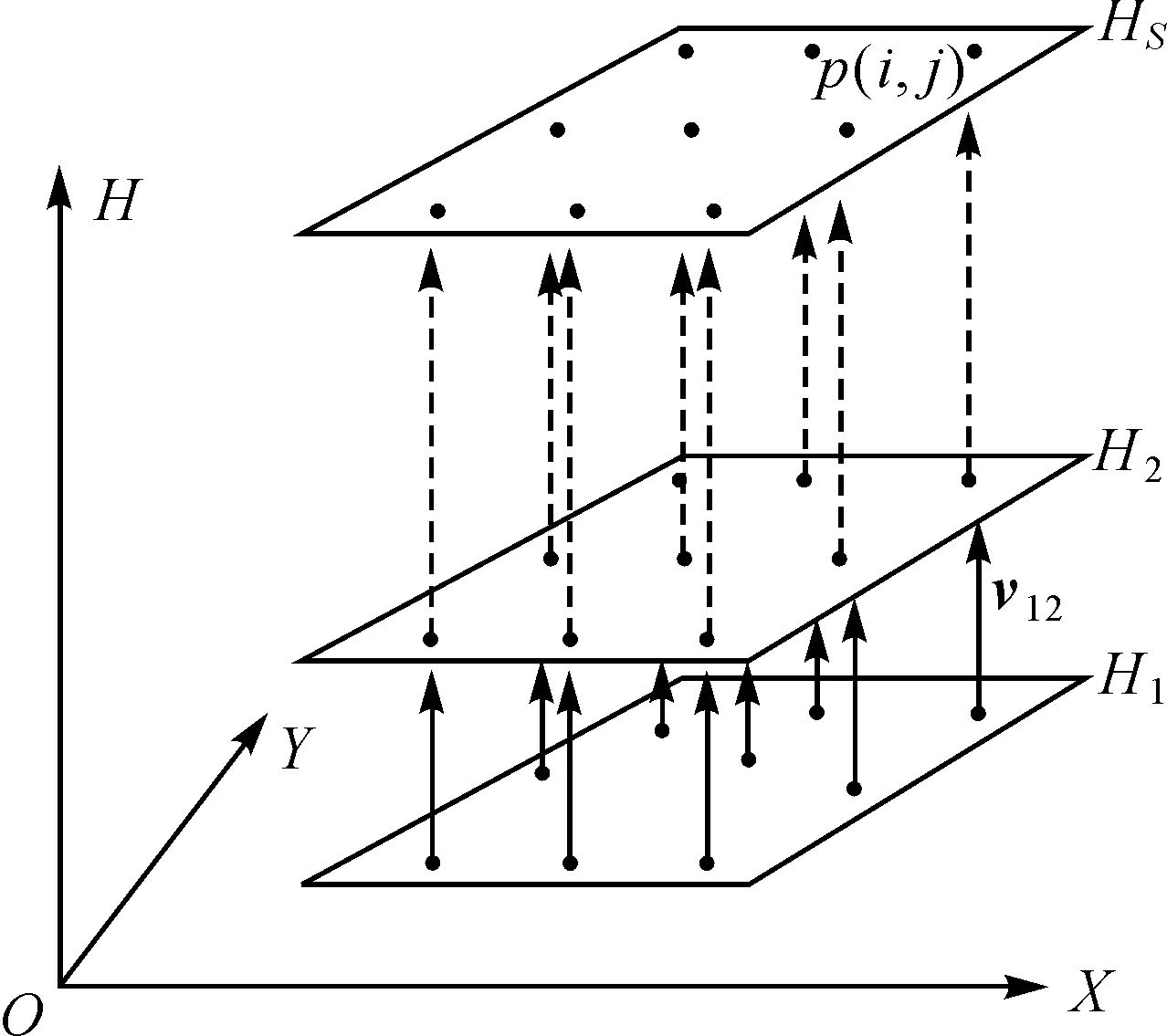
图4 恢复视线向量Fig.4 Reconstruction of line-of-sight vector
视线向量还可以采用指向角的形式进行描述,按照这个思路,结合卫星平台运行的轨道高度,可以恢复出成像时刻的位置信息和姿态信息,从而建立物方点与投影中心之间的对应关系,如图5所示。由于与真实的外方位元素定义并不相同,恢复出来的位置和姿态参数称为虚拟外方位元素。卫星在高轨道空间绕地球飞行,其轨道运行高度比较稳定,而且由轨道高度引起的定位误差非常小[6],因此,利用轨道高度值恢复虚拟外方位元素从理论上是可行的。

图5 恢复虚拟外方位元素Fig.5 Reconstruction of pseudo elements of exterior orientation
根据图5所示的几何关系,可以计算得到
(4)
(5)
式中,(ψX,ψY)表示视线向量在大地坐标系下的指向角,HS表示卫星平台运行的轨道高度。
摄影中心和物方点之间的关系还需要一个旋偏角来进行描述,将其表示为ψZ,对于高分辨率卫星,其值比较小,可以将它的初值设为0。至此,描述摄影中心和物方点之间对应关系的虚拟外方位元素(XS,YS,Hs,ψX,ψY,ψZ)已完全恢复。从几何意义上对恢复的虚拟外方位元素进行分析,其3个线元素代表的是成像时刻传感器的经度、纬度和大地高,3个角元素表示成像光线在大地坐标系下的指向角以及投影中心和物方点之间的旋偏角。虽然与真实的外方位元素表示方式存在区别,但其本质都是为了描述传感器成像时刻的位置和姿态。
2.2 构建误差方程
对于任一控制点或连接点,根据图5所示的几何关系,可建立以虚拟外方位元素描述的成像方程如下
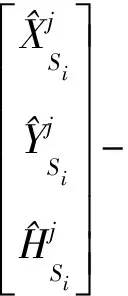
(6)

消去式(6)中的比例因子λ,得到控制点或连接点的观测方程为
(7)
根据视线向量和轨道高度恢复的虚拟外方位元素并不准确,还需要对其进行误差建模
(8)

(9)
式中,ai、bi、ci、di、ei、fi(i=0,1,2)是多项式系数;sample、line是像点坐标。
将式(8)和式(9)代入式(7)后进行线性化处理,可以得到附加视线向量修正的区域网平差误差方程式的矩阵形式
V=AX1+BX2-L
(10)
式中,X1表示多项式参数的改正数向量;X2表示地面点坐标的改正数向量;A和B分别表示对应未知数X1和X2的系数矩阵;V表示观测值残差向量;L表示观测值向量。
按照式(10)列出误差方程后,采用边法化边消元的方法先解算出虚拟外方位元素补偿模型参数,然后按照式(7)求解地面点坐标,整个过程迭代进行直到未知数改正数小于设定阈值。
3 试验与分析
3.1 试验数据与方案设计
为充分验证本文算法的有效性,采用模拟数据和真实数据对模型参数以及算法性能进行全面试验,此外,还进行了相同配置下的传统区域网平差试验,以更好地对比传统方法和本文方法的差异。
生成模拟数据的原始数据为覆盖美国华盛顿地区的1景资源三号(ZY-3)三线阵立体影像,获取时间为2012年5月,该地区地势平坦,高程范围为0~150 m。该套数据附带可构建严密几何模型的星历数据文件,试验中将其作为原始数据生成一系列模拟数据进行仿真试验。仿真试验的基本思路是,首先根据星历数据文件构建以欧拉角表示的严格几何模型,再通过在外方位元素上添加不同大小的系统误差生成一系列带误差的模拟数据,然后分别采用传统方法和本文方法进行系统误差补偿。仿真试验采用的控制点由原始数据生成,具体做法是:在影像像面上按照1000像素的采样间隔选取一个像点,根据原始星历数据将采样点解算到测区平均高程面上,得到像点对应的物方坐标。
真实数据选取覆盖两种不同地貌区域,且包含不同立体观测模式的多套数据进行试验。两块试验区域分别为河南省嵩山测区和黑龙江省齐齐哈尔测区,其中嵩山测区地貌以丘陵为主,高程范围为0~1600 m;齐齐哈尔测区地貌以平原为主,高程范围为100~400 m。试验数据包括采用多线阵立体模式的ZY-3 02、TH-1三线阵影像、采用宽幅立体模式的GF-1宽幅相机影像以及机动立体模式的GF-2全色影像,各套数据的基本参数见表2。

表2 试验数据基本参数
数据1和数据3为测绘卫星数据,其姿态角测量精度、视场角大小及交会角情况都非常良好,可以进行稳定的立体测图;数据2、数据4、数据5为非测绘卫星数据,由于卫星的制作和安装、轨道姿态以及成像目标自身的影响,将其用于平差将会产生较大的平面和高程误差。其中,数据2和数据4为GF-1宽幅相机数据,相机视场角为16.44°,幅宽可达200 km,星下点分辨率为16 m;数据5为GF-2全色相机数据,星下点分辨率为1 m。需要说明的是,数据1、2、4、5采用的控制点物方坐标在高精度地理信息产品上人工采集所得,精度为分米级;数据3中的控制点物方坐标采用差分GPS技术实地测量获取,精度为厘米级。所量测控制点均为影像上可明显分辨的特征点,像点量测精度约为1~2个像素。
为全面验证本文方法的精度特性,设计了若干试验方案。为保证结果的客观性,试验中涉及的传统区域网平差试验均由商业软件完成,且每次对比试验保证在同一套控制数据和检查数据的情况下进行。
试验1:虚拟外方位元素补偿模型试验。通过试验确定合理的误差补偿模型。
试验2:高程面组合和轨道高度对算法精度影响试验。为了研究高程面组合和轨道高度对算法精度的影响,设置不同的高程面组合和轨道高度值进行试验。
试验3:模拟数据试验。为了验证本文算法的有效性,分别利用传统方法和本文方法对带不同误差的模拟数据进行单片系统误差补偿试验。
试验4:真实卫星数据试验。设置不同的控制点配置方案,利用真实数据进行传统区域网平差和附加视线向量修正的区域网平差试验。
3.2 试验结果及分析
3.2.1 虚拟外方位元素补偿模型试验
式(9)所示的改正模型参数较多,考虑到卫星平台的运行特点,轨道高度HS和旋偏角ψZ的变化其实是非常小的,可以对模型进行合理精简。根据上述分析,采取了以下几种不同的参数设置方案来进行试验:①a0~f3,共18个参数;②a0~b3,c0,d0~e3,f0,共14个参数;③a0~b3,d0~e3,共12个参数;④a0、b0、c0、d0、e0、f0,共6个参数;⑤a0、b0、d0、e0,共4个参数。
本试验采用模拟数据进行,根据当前卫星平台位置和姿态的在轨测量水平,在3个线元素上同时添加10 m的误差,3个角元素上同时添加0.000 05 rad(≈10″)的误差,利用10个均匀分布的控制点对生成的带系统误差的有理函数模型进行单片系统误差补偿,得到前视、下视和后视3幅影像的试验结果见表3。
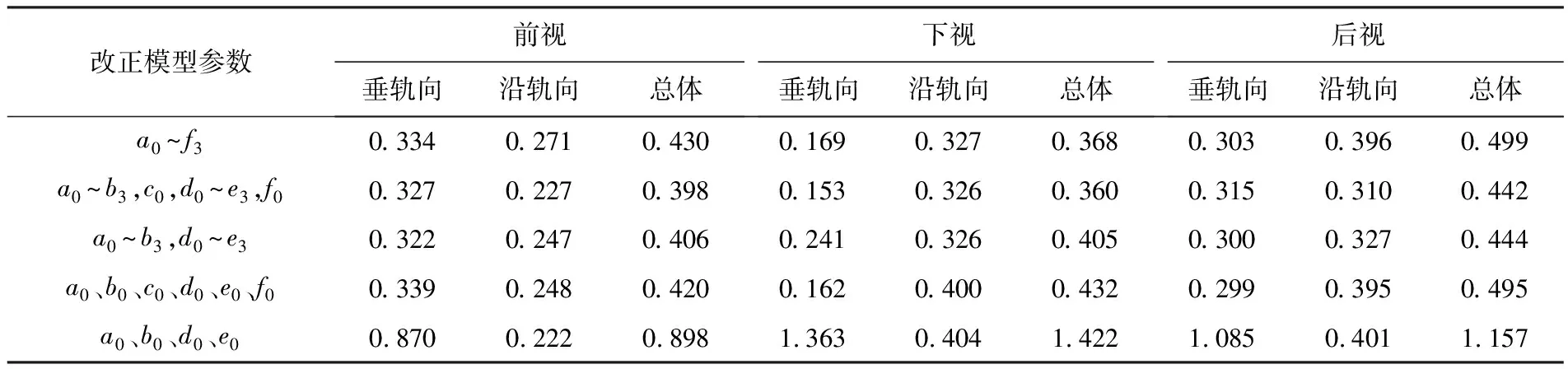
表3 不同改正模型检查点精度统计
从表3所示的试验结果可以看出,附加视线向量修正的卫星影像几何定位方法是有效的,不管采用哪种虚拟外方位元素改正模型,控制点信息的引入都可以一定程度的削弱系统误差。这表明,通过RFM模型恢复地面点成像时刻虚拟外方位元素,从系统误差产生原因的角度进行建模的策略是可行的。不同的改正模型优化的效果存在差异,其中最差的就是4参数模型,经过补偿后像方残差仍然在1个像素左右。除去4参数模型,采用其他改正模型进行补偿后,像方残差基本都接近于有理函数模型的拟合精度。理论上18参数模型应该取得的精度最好,但由于本试验仅采用了10个控制点进行解算,多余观测数较少,因此精度比14参数模型略差,但如果控制点数量非常充足,还是建议采用18参数模型进行补偿。总体来看,3幅影像都是采用14参数模型进行改正时的精度最优,而且控制点需求量要小于18参数模型,因此,本文将以14参数模型作为虚拟外方位元素的改正模型进行后续试验。
3.2.2 高程面组合和轨道高度对算法精度影响试验
虚拟外方位元素的恢复与两个高程面的组合和轨道高度值的取值相关,本试验置了多种相异高程面的组合以及若干轨道高度值来进行试验,其中,轨道高度值的设定是通过在厂商公布的平台轨道高度值上添加一定偏差值来实现。每个高程面的组合或轨道高度值都进行两组试验,一组试验不利用控制点进行补偿,直接采用虚拟外方位元素初值计算新RPC参数;另一组试验利用10个控制点求取模型参数,对视线向量进行修正后再计算新RPC参数。利用新RPC参数求取检查点像方残差,并将结果与利用标称轨道高度值和平均高程范围求取的检查点残差进行比较,两者的差值用于评价高程面组合或轨道高度值对算法精度的影响。
在高程面影响试验中,按照高程起伏范围设置了5个不同的组合进行试验,试验结果如图6和图7所示。

图6 不同高程面组合对精度影响(无控)Fig.6 Influence of different elevation planes settings on positioning accuracy (without GCPs)
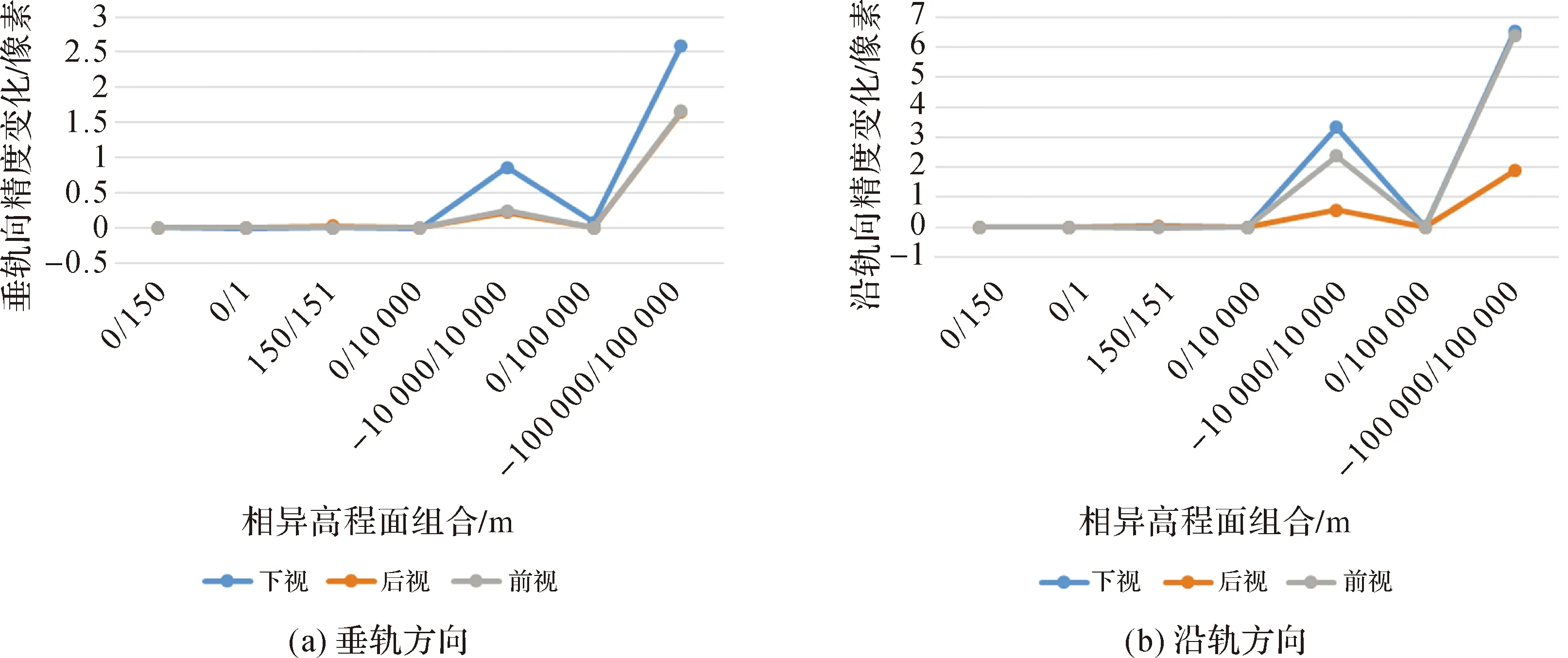
图7 不同高程面组合对精度影响(10个控制点)Fig.7 Influence of different elevation planes settings on positioning accuracy (10 GCPs)
从试验结果可以看出,高程面组合只要设定在合理范围内,定位精度的变化都非常小;最高高程比最低高程对精度的影响更大,尤其是在没有控制点进行系统误差补偿的情况下,这种影响更加明显;无论是否进行系统误差补偿,沿轨向的精度变化都比垂轨向大,这表明沿轨向比垂轨向对高程面组合的设定更加敏感;在利用控制点进行误差补偿时,精度变化减小至像素级,表明控制点信息的引入可以有效地削弱视线向量造成的影响。
在轨道高度影响试验中,设置了从±100 m到±10 km的若干不同轨道偏差值,试验结果如图8和图9所示。
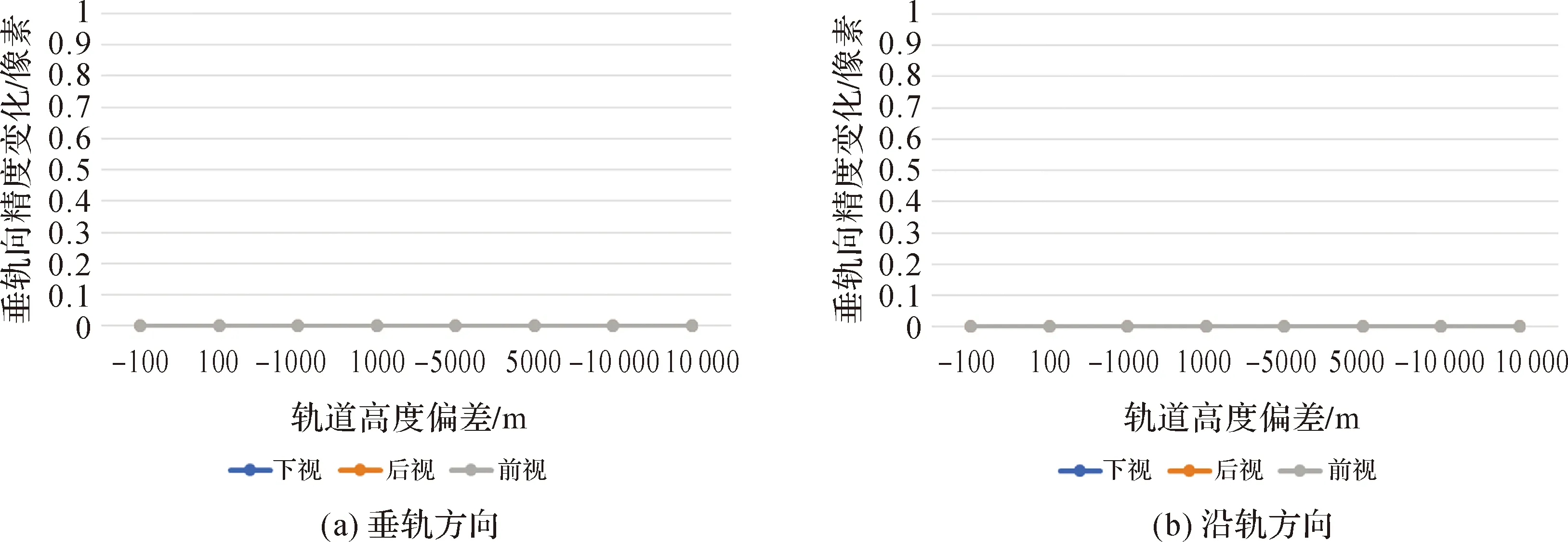
图8 不同轨道高度对精度影响(无控)Fig.8 Influence of different orbit height on positioning accuracy (without GCPs)
图8和图9为不同轨道高度值的试验结果,可以看出,在不进行系统误差补偿的情况下,轨道高度值对定位无影响。因为从理论上来讲,虚拟外方位元素根据轨道高度值计算所得,它们之间存在着固定的比例关系,在不利用控制点更新模型参数的情况下,这种关系是保持不变的。因此,改变轨道高度值的设定并不会对定位精度造成影响。利用控制点进行系统误差补偿时,轨道高度值对定位精度的影响非常小,即使将轨道高度设定为与标称轨道高度偏差10 000 m,其对精度的影响在垂轨向不超过0.01像素,沿轨向不超过0.005像素。
根据上述试验结果和分析,在实际使用中,高程面组合应该尽量贴近测区范围的真实情况,轨道高度值的设定对定位精度的影响不大,使用厂商公布的轨道高度即可。后面的区域网平差实验将按此原则进行计算。
3.2.3 模拟数据试验
为更好地对比本文方法和传统方法的差异,模拟生成了一系列带不同大小误差的有理函数模型,分别利用两种方法进行系统误差补偿。表4所示为10个控制点情况下,由原始下视影像生成的模拟数据的试验结果。

表4 模拟数据试验精度统计
根据误差补偿的结果,绘制了检查点的像方残差分布图,其中编号10试验的检查点残差分布如图10所示。
从试验结果可以看出,当不存在外方位元素误差时,利用传统方法和本文方法进行误差补偿后的定位精度约为0.35像素,此误差可以视为RFM模型的拟合误差。
对于线元素误差,两种方法均能有效进行消除,且补偿后的定位精度基本接近于拟合误差;传统方法对线元素误差的补偿效果要略优于本文方法,但两者差别非常小,当线元素各方向上的误差增加至1000 m时,两者的差别仍在0.05像素以内。针对目前卫星轨道位置测量可达到的精度水平,可以认为两者对于线元素误差的补偿效果相当。
对于角元素误差,两种方法都能进行一定程度的吸收,但补偿效果有所差别,本文方法对角元素误差的吸收效果要优于传统方法,尤其是当角元素误差增大到0.1 rad时,两者的差距可以达到8.5像素,这表明本文方法比传统方法具有更好的稳定性;按照本文之前的分析,角元素误差对垂轨向的影响比沿轨向复杂,试验结果也表明,当角元素误差逐渐增大时,垂轨向误差要明显大于沿轨向误差,这与本文的分析相吻合;目前的姿态角测量精度虽然远优于0.1 rad,但对于某些大视场角相机,角元素误差造成的影响更加明显,因此在传统方法无法有效提升的情况下,本文方法可以达到比传统误差补偿方法更高的精度。
3.2.4 真实卫星数据试验
采用真实卫星数据进行不同数量控制点配置的传统区域网平差和本文平差方法的对比试验,不参与平差的控制点全部作为检查点进行精度统计,以检查点中误差作为评价指标。测绘卫星数据的试验结果见表5,非测绘卫星数据的试验结果见表6。

图9 不同轨道高度对精度影响(10个控制点)Fig.9 Influence of different orbit height on positioning accuracy (10 GCPs)
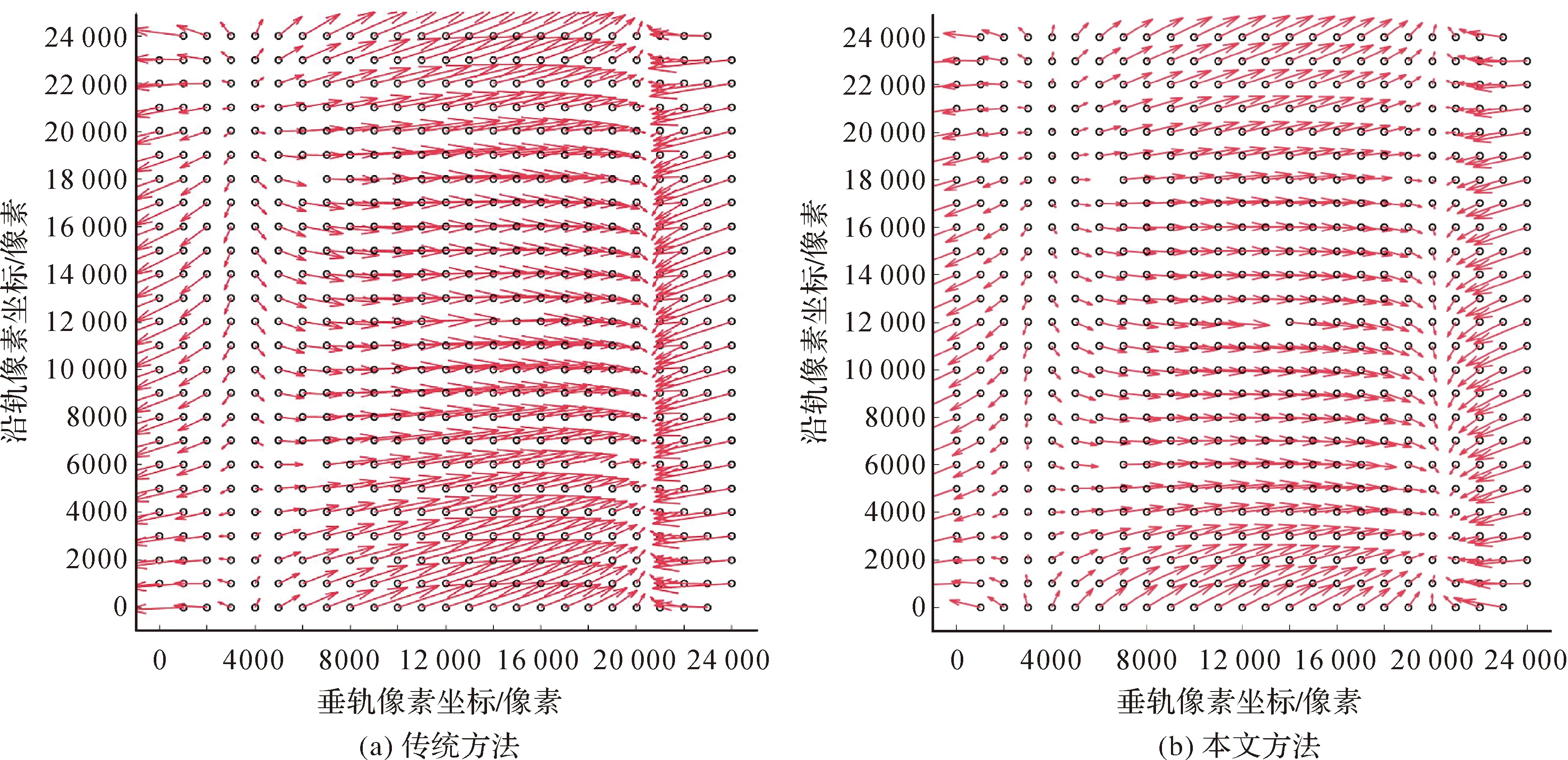
图10 编号10试验检查点残差分布(放大100倍)Fig.10 Checkpoint residual distribution of scheme10 (magnified 100 times)

表5 测绘卫星数据试验精度统计
从表5的统计结果可以看出,对于无控制点的自由网平差,附加视线向量修正的区域网平差可达到与传统方法相当的平面精度,其中嵩山地区的平面精度甚至还要优于传统方法;但其高程精度相当低,与传统方法的结果根本不在一个数量级。这是因为,初始虚拟外方位元素毕竟是由视线向量恢复所得,视线向量的求解精度会影响定位结果,此外,虚拟外方位元素计算过程中的舍入误差也不容忽略,从式(4)可以看出,ψX和ψY的量级是比较小的,实际计算中大概在10-8~10-9,这两者造成的影响必须通过控制点信息对恢复出的初始虚拟外方位元素进行调节才能使其趋于真实情况。添加稀少数量控制点后,两种方法均可有效消除区域网的系统偏移,使定位精度得到提升,这一点对于未经几何检校的ZY-3数据尤其明显。从精度改善百分比可以看出,在控制点数量不充足时,本文方法的提升效果要略低于经典方法;随着控制点信息的增加,两者的精度趋于相当,这说明对于成像条件比较好的测绘卫星,本文方法可以达到与传统方法同水平的误差补偿效果。

表6 非测绘卫星数据试验精度统计
从表6的结果可以看出,对于大视场角的GF-1数据,尽管自由网平差的高程精度较低,这是由算法特点造成的,但加入控制点后,本文算法无论在平面方向还是高程方向,可以达到的精度都比传统区域网平差方法的精度要高,这一点在平坦的齐齐哈尔测区表现得更加明显。这表明,对于大视场角相机且姿态测量精度偏低的非测绘卫星平台,从误差产生原因的角度进行建模,比传统方法从误差导致的结果进行建模补偿的效果更好。由于并非三线阵影像,非测绘卫星形成的重叠影像普遍会存在弱交会角的情况,事实上,数据2、数据4和数据5都存在这种情况。对于数据2和数据4,采用传统区域网平差算法还能得到比较可靠的结果是因为人工剔除掉了多度重叠中存在的弱交会光线,如果不进行这种处理,这种弱交会状态将会影响整个区域网平差的质量,使结果出现较大偏差,而本文所述算法则无须考虑这种情况即可得到稳定的结果。对于数据5,同轨相邻影像尽管存在重叠区域,但实际上并不存在视差,而异轨影像间交会角约为5°,这种交会状态使得采用传统方法即使在有控制点的情况下也无法得到结果。而利用本文方法,在充足数量控制点的情况下,最终可以达到平面3.70 m,高程4.96 m的精度水平。传统区域网平差根据成像关系在像方建立观测方程,前方交会求解物方坐标是一个迭代的过程,而当光线近似平行时,需要非常良好的初值才能得到稳定的结果。而本文方法在物方空间根据相似几何关系建立摄影点和地面点之间对应关系,利用该方程求解连接点物方坐标是一个线性方程,并不需要迭代求解;且计算过程中法方程条件数要小于前方交会时法方程条件数。因此,可以削弱由光线近似平行时造成的平差结果恶化,在处理弱交会影像定位问题时,还具有不需要辅助DEM数据支持的优势。理论上,本文方法在处理大姿态角误差、大视场角以及弱交会角等各种严苛条件下的卫星影像定位问题时,具有比传统方法更大的优势。
4 结 论
为提高对地观测数据的应用效益,本文提出了一种附加视线向量修正的卫星影像区域网平差方法。该方法从系统误差产生原因的角度进行误差建模,能够避免传统区域网平差方法的条件限制。采用模拟数据对模型重建参数进行了分析,并对比了不同误差大小情况下传统方法和本文方法的精度差异。试验结果表明,常规情况下,本文方法可达到与传统方法相当的精度;当姿态角误差较大时,可以达到比传统方法更高的精度,最高可优于经典方法8.5像素。在此基础上,选取两块不同地貌试验区共5套真实数据进行试验,并将结果与传统区域网平差算法进行了比较。试验表明,附加视线向量修正的区域网平差方法是有效可行的,尽管无控条件下的高程精度不理想,但少量控制点信息的引入即可消除这种影响,该方法处理测绘卫星数据可以达到与传统方法相当的精度;处理非测绘卫星数据时,可达到比传统方法更高的精度,并且能够削弱区域网内弱交会状态造成的恶化。理论上,采用该方法处理大姿态角误差、大视场角以及弱交会角等各种严苛条件下的卫星影像能达到比传统方法更好的效果。
