Swarm系列卫星非差运动学厘米级精密定轨

张兵兵，牛继强，王正涛，徐 丰，田坤俊

1. 信阳师范学院地理科学学院，河南 信阳 464000； 2. 信阳师范学院河南省水土环境污染协同防治重点实验室，河南 信阳 464000； 3. 武汉大学测绘学院，湖北 武汉 430079

欧空局(European Space Agency，ESA)于2013年11月22日成功发射Swarm卫星，称为小卫星“地球探测”计划。该计划不仅用于探测地球磁场信息，还用于探测地球大气层和重力场恢复等[1]。Swarm星群由3颗相同的卫星组成，分别命名为Swarm-A、Swarm-B和Swarm-C。其中，Swarm-A和Swarm-C卫星在轨道高度为470 km、倾角为87.4°的极轨道平行飞行，Swarm-B卫星在轨道高度为520 km、倾角为88°的极轨道飞行[2]。Swarm系列卫星精密定轨不仅是整个Swarm星群计划顺利实施的关键，也是有效利用卫星荷载开展地磁场反演等相关科学研究的前提条件。

Swarm卫星上搭载了一系列先进的科学仪器。为了探测地球磁场的强度和方向，每颗Swarm卫星安装有矢量磁力仪和标量磁力仪；地球的电场信息则通过相应的电场仪器设备测量，该设备由朗缪尔探针和热离子成像仪组成；Swarm卫星上安装有加速度计，主要用于测量Swarm卫星非保守力加速度，该数据不仅用于获取热层密度和风的一些信息，还可以用该数据参与地球重力场恢复工作；Swarm卫星上的星载GPS接收机主要用于Swarm卫星精密轨道的确定；Swarm卫星上的激光反射棱镜观测的数据用于检核Swarm卫星轨道[3]。Swarm卫星星载GPS观测数据和解算得到的轨道不仅可以用于地磁场位置标定，也可以用于电离层研究、热层密度的确定及地球重力场的恢复等[4]。

近年来，低轨卫星运动学定轨引起了学者们的极大兴趣。与简化动力学定轨相比，运动学定轨方法不采用任何低轨卫星动力学信息(如重力场、大气阻力等)。因此，运动学定轨结果可用于反演地球重力场模型[3,5]。

Swarm卫星发射之后，国外学者围绕Swarm卫星定轨展开相关学术研究。文献[2]利用超过一年的星载GPS观测数据进行Swarm卫星运动学和简化动力学定轨。SLR检核结果表明，欧空局发布的简化动力学轨道精度约为2.5 cm，运动学定轨精度约为4 cm；运动学轨道与简化动力学轨道3D差值RMS为4～5 cm，在地磁极和地磁赤道的轨道差异会更大。文献[5]解算18个月的Swarm卫星运动学轨道，并进行重力场恢复工作。文献[3]利用PPP技术开展Swarm卫星运动学定轨工作，取得了较好的定轨结果。

国内方面，相关学者开展Swarm卫星简化动力学定轨的相关研究。文献[6]研究天线相位中心改正及其对Swarm卫星简化动力学定轨的影响。文献[7]研究伪随机脉冲先验标准差对Swarm卫星简化动力学定轨的影响。此外，文献[8—9]利用优化的伪随机脉冲进行Swarm卫星简化动力学定轨，定轨结果与欧空局发布的轨道结果精度相当。国内学者主要研究Swarm卫星简化动力学定轨，而关于Swarm卫星非差运动学精密定轨的相关研究却鲜见报道。由于GRACE卫星已于2017年6月停止工作，而GRACE Follow-On于2018年5月成功发射，相关数据最早于2019年才公布，在此期间，Swarm卫星将填补因GRACE无法工作与GRACE Follow-On公布数据之前的空白，继续监测地球重力场信号[10]。而恢复地球重力场模型需要Swarm卫星运动学精密轨道。因此，自主开展Swarm卫星非差运动学精密定轨和精度评定等相关研究有很强的现实意义。

本文采用2015年5月24日—30日的Swarm星载GPS双频观测数据，基于MW和消电离层线性组合，在精密单点定位技术的基础上，采用批处理最小二乘估计法对不同轨道高度的Swarm系列卫星进行非差运动学精密定轨。利用星载GPS相位观测值残差、与欧空局发布的简化动力学轨道对比，以及SLR检核3种方法对Swarm系列卫星非差运动学定轨结果进行精度评估。检验运用Swarm星载GPS双频观测值进行非差运动学精密定轨的可行性方案与定轨结果的可靠性。

1 Swarm卫星非差运动学定轨原理与方法

1.1 星载双频GPS载波相位观测模型

Swarm星载GPS双频接收机测量两种不同频率的载波相位，基本的相位观测方程如下[11]

(1)

为了消除电离层延迟的影响，本文对相位观测方程进行消电离层组合，结果如式(2)所示[11]

(2)

综合考虑式(1)和式(2)，Swarm卫星非差消电离层组合相位观测方程为

(3)

式(3)中的相位非差观测值是相对于天线相位中心的，而CODE中心提供的GPS精密星历是相对于卫星质心的，因此需要将GPS卫星位置改正到天线相位中心，并在精密定轨时将其作为位置基准，在此基础上，综合考虑相对论效应、天线相位中心改正以及地球旋转效应等因素的影响，采用批处理最小二乘估计法进行轨道参数估计，进而获得Swarm卫星非差运动学轨道。

目前最小二乘估计法是卫星精密定轨最主要的方法之一，该方法解算精度高且稳定，主要应用于高精度事后精密定轨。由于Swarm卫星运动学定轨的主要目的之一是为了解算地球静态和月时变重力场模型提供精密轨道[12-21]，因此，该方法在Swarm卫星运动学定轨中有广泛的应用。学者们围绕Swarm卫星运动学定轨工作展开了一系列的研究工作。文献[12]在精密单点定位的基础上，综合考虑各种系统误差的影响，直接采用原始的伪距和相位观测值进行批处理最小二乘估计，进而获得Swarm卫星运动学轨道，获得了厘米级的定轨精度，该方法中观测值无须进行线性组合。文献[2]利用GNSS高精度的定轨软件(GNSS high-precision orbit determination software tools，GHOST)进行Swarm卫星运动学定轨。该软件采用非差观测值和标准贝叶斯加权最小二乘估计法，定轨精度达到厘米级，欧空局发布的轨道即此软件计算得到。文献[13]采用非差相位观测值，综合考虑天线相位中心改正、相对论效应改正以及其他影响轨道精度的误差改正等因素，采用最小二乘估计法估计Swarm卫星运动学轨道和相关的参数(如接收机钟差参数和载波相位模糊度参数等)，定轨精度也达到了厘米级。本文为了实现自主定轨的需要，围绕Swam卫星非差运动学精密定轨展开研究，与已有的运动学定轨工作相比，主要集中体现在观测数据的预处理以及定轨解算策略的选取等方面有所差异。

1.2 数据来源与解算策略

1.2.1 数据来源

采用欧空局提供的Swarm星载双频GPS观测值、欧洲定轨中心提供的15 min采样间隔的GPS事后精密星历、地球自转参数(earth rotation parameter,ERP)以及5 s采样间隔的GPS卫星精密钟差等数据，由于Swarm卫星的一个重返轨道为4 d[22]，因此，本文选取一个星期的观测数据参与解算，时间段为2015年5月24日—30日(DOY 144—150)，定轨弧长为24 h。

1.2.2 解算策略

根据Swarm卫星非差运动学精密定轨的基本原理可知，与相位观测值有关的因素均会影响到最终的定轨结果，根据来源不同，本文制定了详细的解算策略。

(1) 提高观测数据的质量。“干净”的Swarm卫星相位观测值是非差运动学精密定轨的前提条件。本文联合MW线性组合和消电离层组合对伪距和相位观测值粗差和周跳进行探测[23]。此外，消电离层相位和伪距组合还可以有效消除电离层延迟的影响，其中伪距观测值仅用于初始轨道的确定，消电离层相位观测值采用COMBINED算法进一步对周跳进行有效探测[11]，如果历元周跳探测后仍不能有效改正，则在此处加入一个模糊度参数，从而获得“干净”的非差消电离层相位观测值。

(2) 由于GPS卫星星历和钟差具有空间位置基准的作用，产品精度的好坏会直接影响Swarm卫星非差运动学定轨精度。因此，本文采用欧洲定轨中心发布的GPS事后精密星历和卫星钟差参与非差运动学轨道解算。

(3) 相位观测值权重。第1种方案为所有相位观测值权重相同，第2种方案为相位观测值权重采用与高度角e相关的函数：W(e)=cos2(e)，第3种方案为相位观测值权重采用与高度角e相关的函数：W(e)=cos4(e)。

(4) Swarm星载GPS双频非差消电离层相位观测值作为基本观测值，相位观测值先验标准差设置为1 mm，引入以上3种不同的相位观测值权重方案，综合考虑相对论效应、天线相位中心改正、相位缠绕、硬件延迟以及地球旋转效应等因素的影响，批处理最小二乘法[24-25]和参数预消除技术[11]用于未知参数的估计，包括Swarm卫星位置和钟差以及模糊度参数等。

为了获取较好的相位观测值权重，本文选取2015年5月24日1 d的Swarm-A/B/C卫星观测数据参与3种相位观测值权重方案的计算，分别将3种权重方案获得的定轨结果欧空局发布的简化动力学轨道进行对比分析。结果如图1所示。由图1所知，3种权重方案均能让Swarm-A/B/C卫星1D RMS达到了厘米级，此外，对于Swarm-A/B/C卫星，方案2获得的定轨精度优于方案1和方案3，因此，本文选取方案2作为相位观测值的权重函数参与计算。综上所述，本文Swarm系列卫星非差运动学定轨数据处理策略见表1。

图1 Swarm系列卫星3种权重方案定轨精度统计Fig.1 Orbit determination accuracy statistics of three weight schemes of Swarm satellites

表1 Swarm系列卫星非差运动学定轨数据处理策略

2 Swarm系列卫星非差运动学定轨精度评估

当前，低轨卫星轨道精度评估方法一般分为内符合精度评估和外符合精度评估。内符合精度评估的基本方法是依据低轨卫星定轨过程中获取的相关数据或结果进行对比分析，例如对观测值残差进行统计分析[8]。外符合精度评估的基本方法是通过与国际权威机构发布的轨道进行对比分析或者利用未参与精密定轨的其他观测数据(如卫星激光测卫数据)进行精度评估。本文将从内符合精度和外符合精度两个方面全面评估Swarm系列卫星非差运动学定轨精度。内符合精度评估：对星载GPS相位观测值残差进行统计分析。外符合精度评估：①将本文Swarm系列卫星非差运动学定轨结果同欧空局发布的精密轨道进行对比分析。②利用SLR观测数据独立检核Swarm卫星非差运动学轨道。

2.1 相位观测值残差分析

相位观测值残差是评价GPS定轨精度的指标之一[8]，当所采用的观测数据的质量及其预处理都很理想时，观测值残差接近观测噪声水平。图2表示Swarm星载GPS相位观测值残差RMS，表2表示Swarm-A/B/C系列卫星定轨后星载GPS非差相位观测值残差平均RMS，由图2和表2可知，不同年积日不同卫星的相位残差RMS分布在6～7 mm，Swarm-B卫星整体结果优于Swarm-A/C卫星。结果表明：①本文选取的观测模型与实际情况吻合较好；②本文提供的星载GPS数据预处理方法可以较好地探测和处理周跳。

图2 Swarm星载GPS相位观测值残差RMSFig.2 Residual RMS of spaceborne GPS phase observation for Swarm

表2 Swarm星载GPS非差相位观测值残差RMS

2.2 Swarm非差运动学定轨结果与参考轨道对比分析

2.2.1 与欧空局发布的简化动力学轨道对比分析

荷兰代尔夫特理工大学航空工程学院作为卫星星群应用与研究机构(Swarm Satellite Constellation Application and Research Facility,SCARF)的成员之一，负责Swarm卫星精密定轨工作。该学院采用GHOST软件解算Swarm-A/B/C卫星简化动力学轨道，利用地面SLR站观测数据检核该轨道，获得优于2 cm的轨道精度，定轨结果已在ESA网站上发布(swarm-diss.eo.esa.int)[2]。根据表1给出的Swarm卫星非差运动学定轨策略，Swarm系列卫星非差运动学定轨结果与简化动力学轨道进行对比分析，结果见表3和图3—图6。由图3可以发现，在径向、切向及法向上，Swarm-A/B/C卫星轨道差值RMS均在2～4 cm，不同年积日不同卫星的定轨精度差异不大；由图4—图6和表3可以发现，在径向、切向及法向上，Swarm-A/B/C卫星非差运动学定轨结果均无明显的系统误差，定轨精度也比较均匀，均为3～4 cm。因此，Swarm系列卫星径向、切向及法向上非差运动学定轨精度均优于5厘米，满足精度需求。

表3 Swarm卫星非差运动学定轨结果与欧空局简化动力学轨道差值统计结果

2.2.2 与欧空局发布的运动学轨道进行对比分析

欧空局发布的Swarm卫星运动学轨道是采用GHOST软件解算得到[2]，与本文定轨策略不同。该软件运动学精密定轨阶段同时考虑星载GPS伪距和相位观测值，为了消除一阶电离层的影响，采取消电离层组合获得消电离层相位观测值和消电离层伪距观测值，观测值定权方面未采用高度角定权，而是根据根据观测噪声的期望水平定权，消电离层相位观测值的先验值为1 mm，消电离层伪距观测值先验值为1 m；估计方法为标准贝叶斯加权最小二乘估计法。因此，将本文的运动学定轨结果与欧空局发布的运动学轨道进行对比分析，结果见表4和图7。由图7可以发现，在径向、切向及法向上，Swarm-A/B/C卫星轨道差值RMS均在1～2 cm，不同年积日不同卫星的定轨精度差异不大；由图7和表4可以发现，在径向、切向及法向上，Swarm-A/B/C卫星非差运动学定轨结果均无明显的系统误差，与欧空局轨道相比，两者的轨道差值比较均匀，均为1～2 cm。因此，本文计算得到的Swarm系列卫星非差运动学轨道与欧空局发布的运动学轨道精度相当。

2.3 SLR检核

Swarm卫星上安装了激光反射棱镜装置，地面观测站可以对其进行跟踪测量。SLR测距精度可达亚厘米级，此外，对于一些观测条件较好的SLR站，SLR测距精度为几个毫米，因此，SLR成为单次测距精度最高的空间大地测量技术之一[26-27]。由于SLR观测数据独立于星载GPS观测数据，因此，本文采用SLR技术对Swarm卫星轨道进行外部检核。

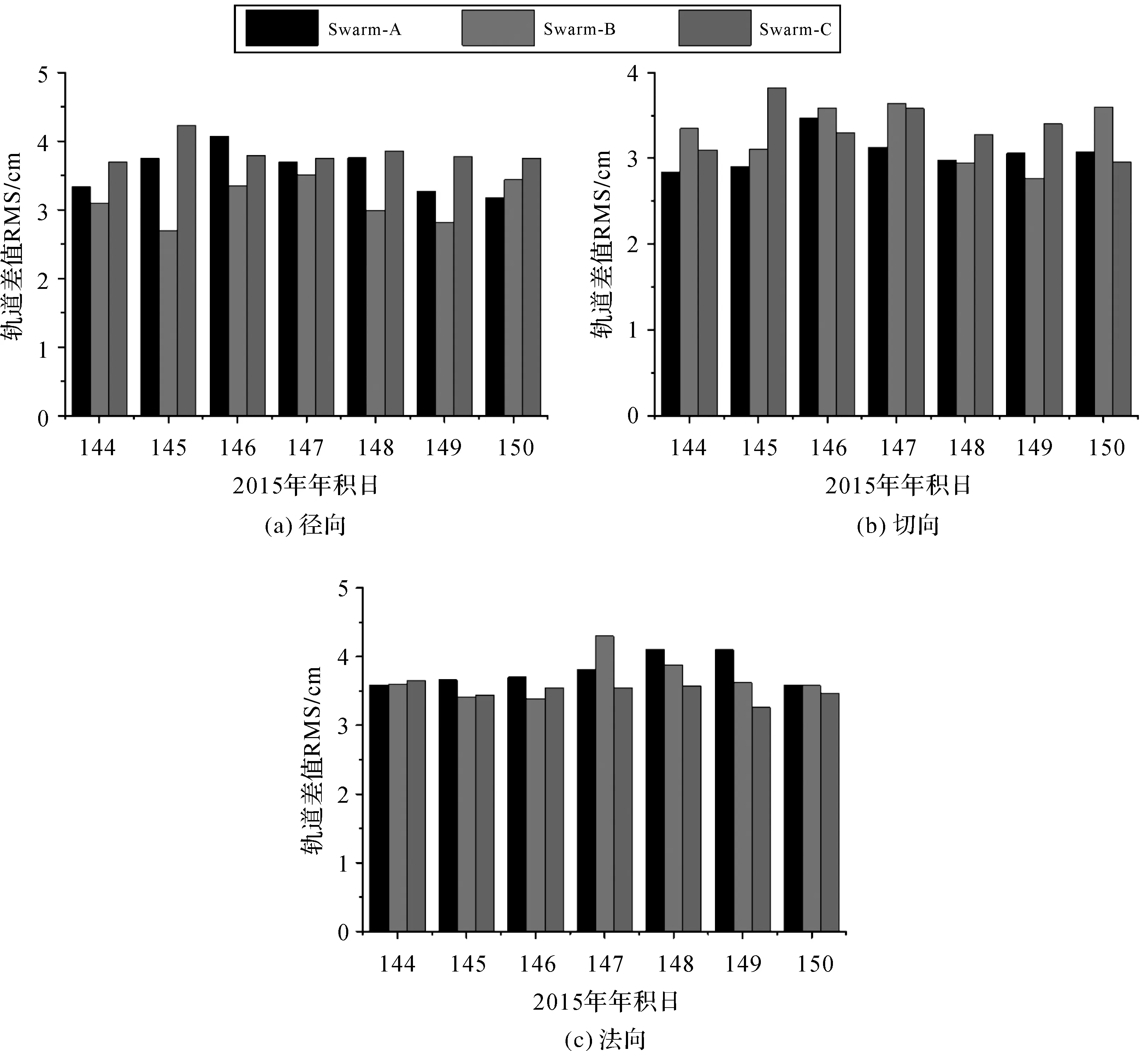
图3 Swarm卫星非差运动学定轨结果与欧空局简化动力学轨道差值RMSFig.3 Difference RMS between Swarm kinematic orbits and ESA reduced-dynamic orbits

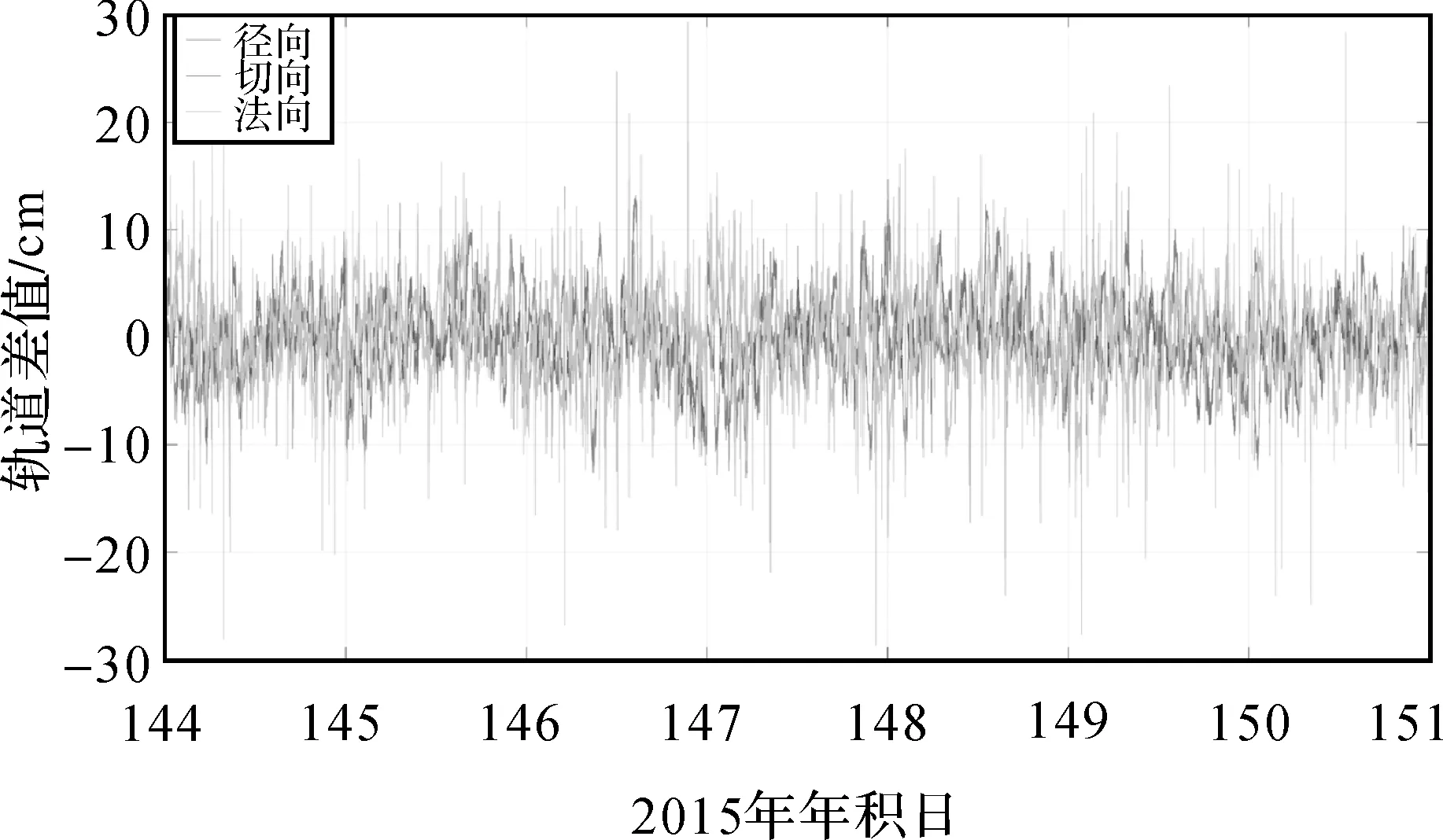
图4 Swarm-A卫星非差运动学定轨结果与简化动力学轨道差值Fig.4 Difference between Swarm-A undifferenced kinematic orbits and reduced-dynamic orbits

图5 Swarm-B卫星非差运动学定轨结果与简化动力学轨道差值Fig.5 Difference between Swarm-B undifferenced kinematic orbits and reduced-dynamic orbits

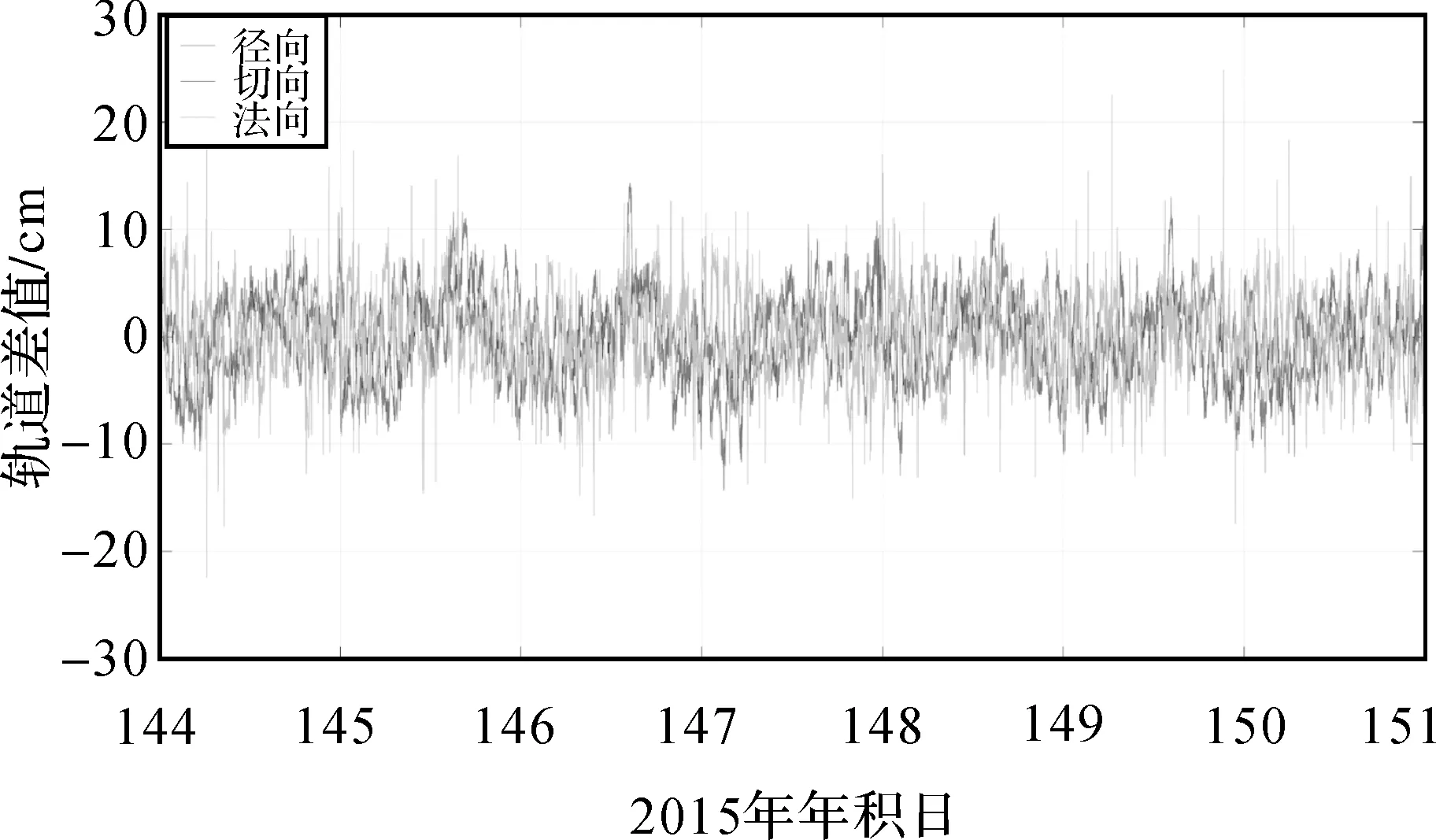
图6 Swarm-C卫星非差运动学定轨结果与简化动力学轨道差值Fig.6 Difference between Swarm-C undifferenced kinematic orbits and reduced-dynamic orbits

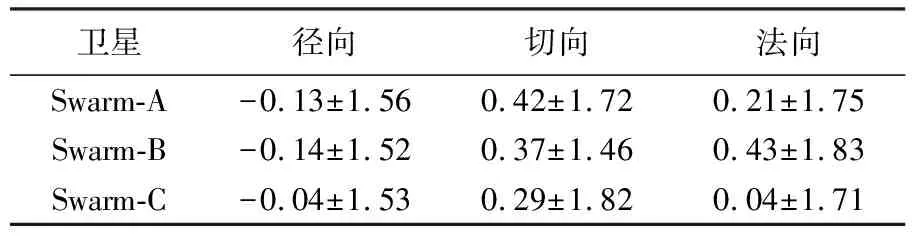
表4 Swarm卫星非差运动学定轨结果与欧空局运动学轨道差值统计结果

SLR观测值对Swarm卫星运动学轨道进行外部检核的过程中，需要综合考虑各种改正模型，进而提高SLR检核的质量，具体的改正模型见表5。

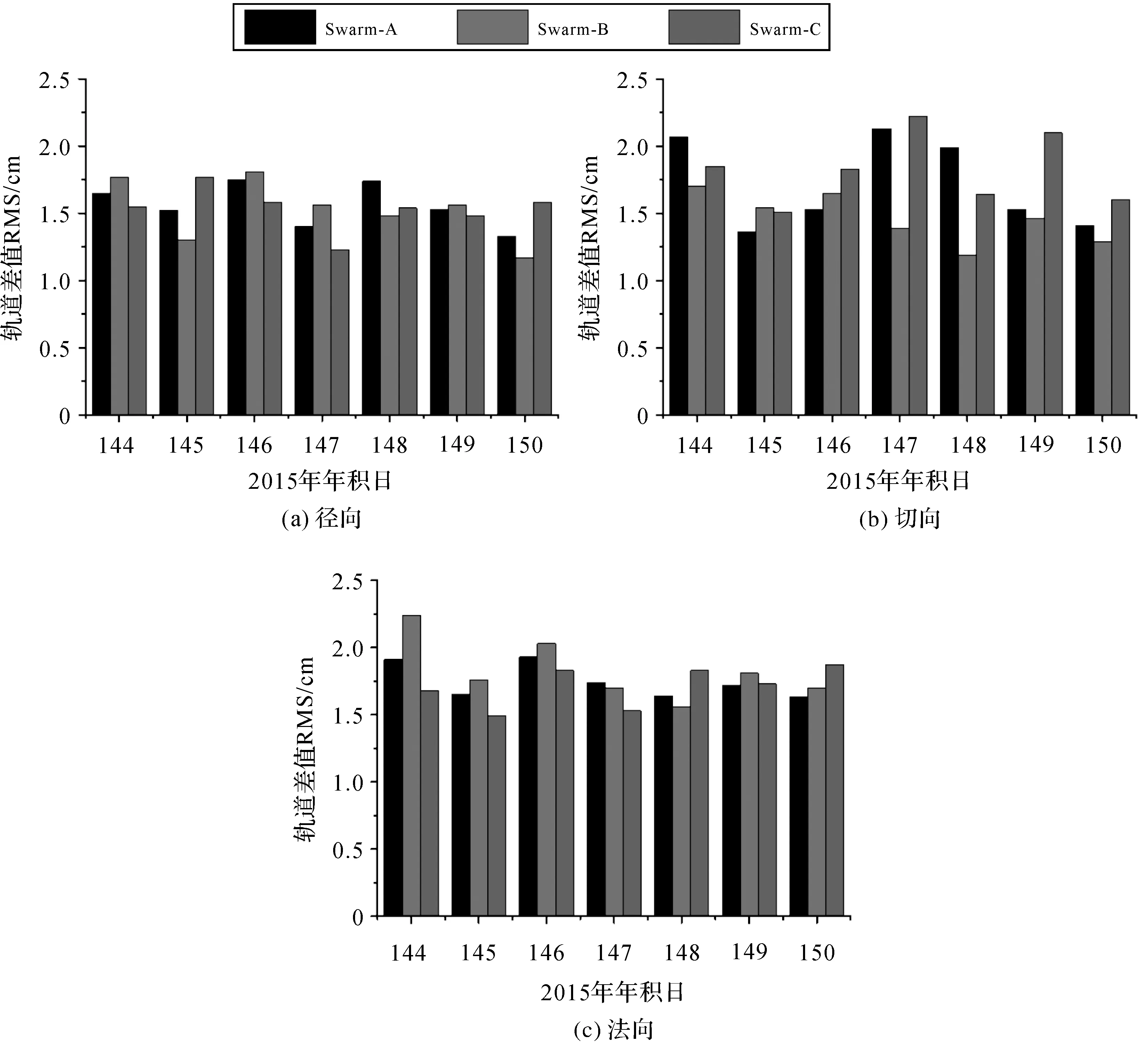
图7 Swarm卫星非差运动学定轨结果与欧空局运动学轨道差值RMSFig.7 Difference STD between Swarm kinematic orbits and ESA kinematic orbits

在2015年5月24日—30日期间，利用SLR观测值对Swarm卫星非差运动学轨道进行检核，SLR地面站的分布见图8。SLR残差统计结果见图9—图11和表5，图9—图11分别为利用SLR观测值检核Swarm-A、Swarm-B和Swarm-C卫星非差运动学轨道的残差图，表6为相对应的SLR残差统计结果。由图9—图11以及表6可知，Swarm-A/B/C卫星非差运动学定轨结果无明显的系统误差，定轨精度良好，其中，Swarm-A卫星非差运动学轨道精度为4.26 cm，Swarm-B卫星非差运动学轨道精度为3.86 cm，Swarm-C卫星非差运动学定轨结果为4.09 cm。

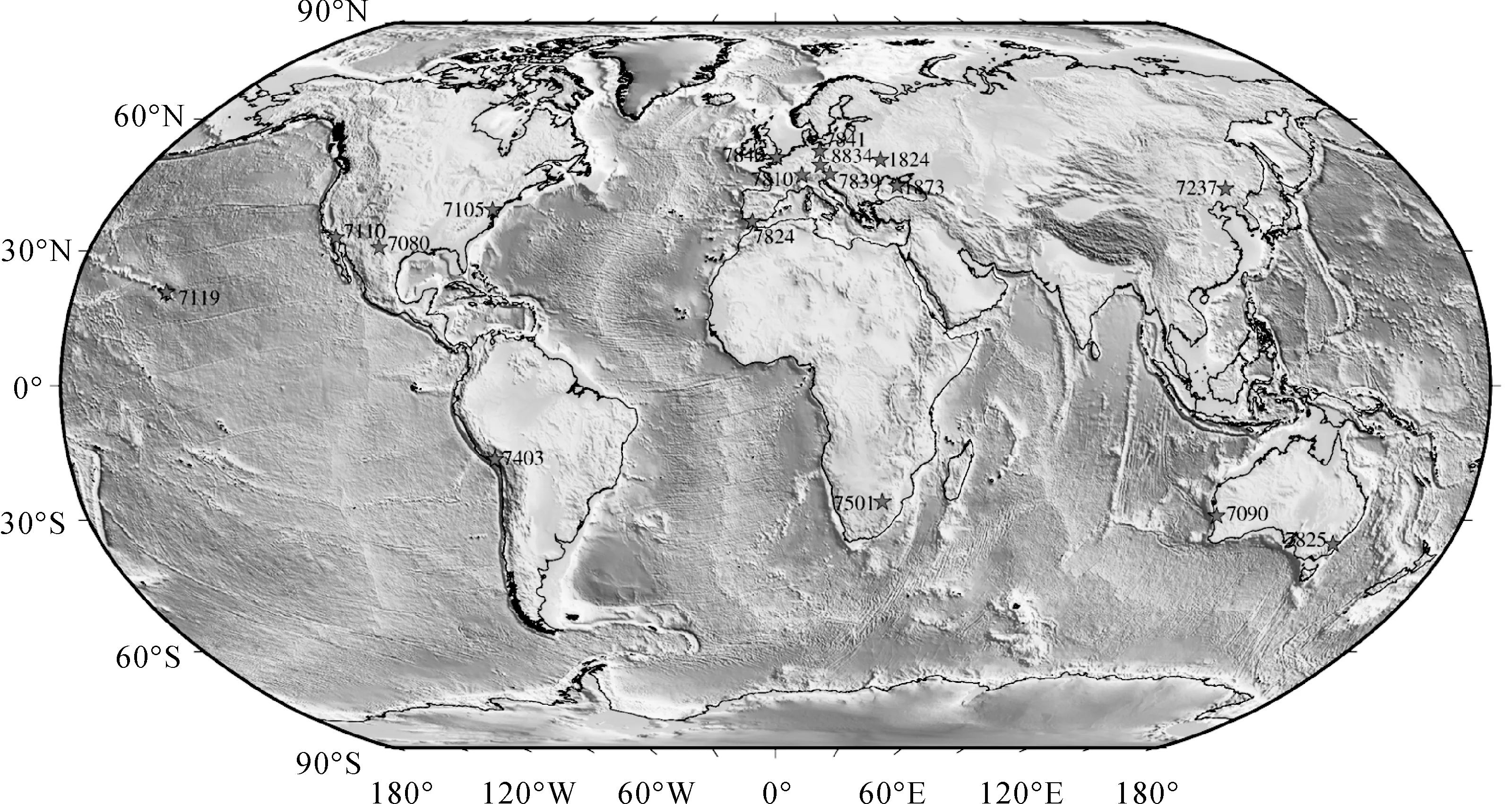
图8 地面SLR跟踪站分布Fig.8 Distribution map of ground SLR tracking station

图9 Swarm-A卫星非差运动学轨道的SLR残差值Fig.9 SLR residual values of Swarm-A undifferenced kinematic orbit

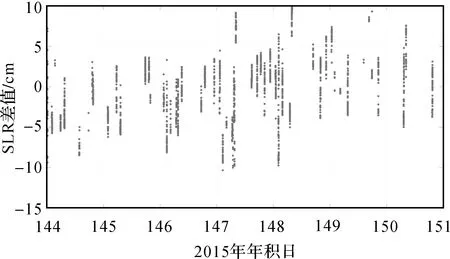
图10 Swarm-B卫星运动学轨道的SLR残差值Fig.10 SLR residual values of Swarm-B undifferenced kinematic orbit

图11 Swarm-C卫星运动学轨道的SLR残差值Fig.11 SLR residual values of Swarm-C undifferenced kinematic orbit

表5 SLR检核Swarm卫星轨道过程中的改正模型

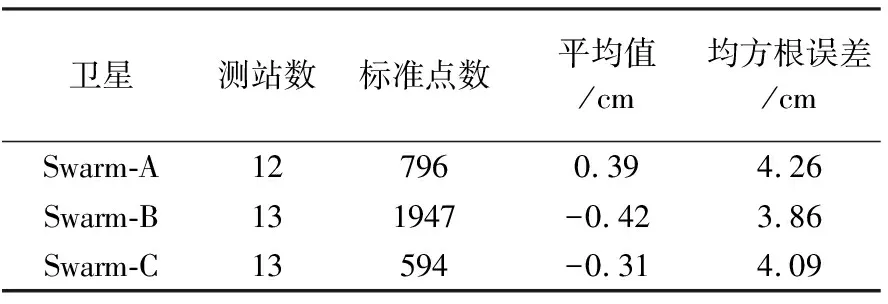
表6 Swarm卫星非差运动学轨道的SLR残差统计结果

3 结 论

采用2015年5月24日—30日的Swarm星载GPS双频观测数据，基于MW和消电离层线性组合，在精密单点定位技术的基础上，采用批处理最小二乘估计法对不同轨道高度的Swarm系列卫星进行非差运动学精密定轨。利用星载GPS相位观测值残差、与欧空局发布的简化动力学轨道对比，以及SLR检核等3种方法对Swarm系列卫星非差运动学定轨结果进行精度评估。Swarm星载GPS相位观测值残差RMS为6～7 mm，星载GPS观测模型较好；与欧空局发布的简化动力学轨道进行对比分析，Swarm-A/B/C卫星径向、切向及法向轨道差值RMS均在2～4 cm；与欧空局发布的运动学轨道进行对比分析，Swarm系列卫星径向、切向及法向轨道差值RMS为1～2 cm，3个方向均无明显的系统误差；利用SLR观测数据对Swarm卫星非差运动学轨道进行独立检核，定轨精度为3～4 cm。

致谢：感谢CODE提供GPS精密星历、卫星钟差及地球自转参数，感谢ESA提供Swarm星载GPS观测数据、姿态数据与Swarm卫星简化动力学轨道，感谢ILRS提供SLR观测数据。