数学建模计算空间路径的方法在爬电距离和电气间隙测量中的应用

汪奕帆 冯秉佑

（嘉兴威凯检测技术有限公司 嘉兴 314000）

引言

在电器产业不断发展的现阶段，各类产品的安全性能已经被越来越多的人所重视，而不同产品的多样性和独特性，又使得确定并测量爬电距离和电气间隙的“最短”路径，变得尤为困难。本文以实际样品来举例，分享一种需要空间桥接的复杂爬电距离问题的解决方案。

1 案例分析

由于爬电距离和电气间隙不符合标准要求而发生的安全事故屡见不鲜，其中最为著名的要数2016年三星手机着火事件，据公开调查结果显示，主要问题来自于采用的SDI电池（图1）。

图1可以清晰的看到，在外部引起电池电极变形后，导致了电池电极之间的爬电距离和电气间隙减小到安全限值以下，引起电池短路，从而导致了着火事件的发生[1]。

可见，确定产品绝缘结构的组成、导电部件和易触及表面，选取正确的爬电距离和电气间隙的路径，并用适合的测量设备确定数据，是取得准确检测结果和防止误判的关键，而其中最短路径的确定则是重中之重。

2 实际举例计算

对于简单的案例我们可以通过直接测量或者简单的展开平面、几何计算，就可以得到相应的爬电距离，但是当实际样品爬电距离需要经过几个面，甚至可能需要空间桥接时，简单的测量、计算已经无法满足我们的要求，下文就以能力验证中的样品来举例，借用一种先建立三维模型，再建立数学模型，最后引入编程计算机计算的思路，重点探讨如何逐步的分析、计算需要空间桥接的复杂爬电距离问题。

2.1 样品简述

本次试验的被测样品为印刷电路板（双面板），如图2和图3。

其中： T1、T2、T3、T4为印刷电路A面的电极，R1、R2为印刷电路B面的电极，中间梯形的区域镂空。

本样品在测试中有如下特殊说明和假定：

①样片中梯形镂空区域的角全部按“尖角”考虑，不视为圆角，∠α=90 °。

②在电气间隙、爬电距离测量时，样片中电极T3、T4、R1、R2与梯形镂空区域边缘按“齐平”考虑。

③爬电距离和电器间隙测量值精确到0.001 mm。

2.2 爬电距离电气间隙的影响因素

爬电距离电气间隙影响因素有很多，如：海拔高度，电场条件，污染等级，桥接（跨接），通过中介物（如有的话）等都会对爬电距离和电气间隙产生不同程度的影响。此例中着重考察污染等级和桥接（跨接）。

污染等级：爬电距离和电气间隙极易受到外来物质污染的干扰，确定污染等级对测量爬电距离和电气间隙非常重要。

图3 样品B面

桥接（跨接）：在电器的长期使用过程中，如灰尘、其它导电微粒会积累在污染绝缘材料表面，导致沿污染物表面形成爬电路径，所以在小尺寸的“间隙”和一定角度下的“槽”，需要着重考虑桥接问题[2]。

2.3 对于实例的分析和思路

试验过程中，最为复杂的部分要属T1与R1中金属部件之间的爬电距离的路径及测量值（2级污染等级和3级污染等级均需测量）。由于T1-R1之间不在同一个平面上，也不能通过简单的展开处理将T1和R1放到同一平面上，这让求解这个爬电距离问题变得复杂了许多。

2.4 三维建模

我们通过三维软件UG进行建模（图4），建立等尺寸的模型有利于我们更好的观察样品，从而分析和寻找最短路径。

2.5 分析路径

通过模型分析，可以得到爬电距离的路径只可能存在3种情况（图5）。

①图5中T1-E-R1路线。

此路径爬电距离可以直接在样品上测得路径为：23.649 20≈ 23.649。

②图5中T1-（EH线段上的某点K1）-I-R1路线。

此路径爬电距离看似不能直接测得，实际上可以将T1-H-E沿着HE展开，使得T1,H,E,G,I在同一平面，此时两点之间线段最短，路径T1-（EH线段上的某点K）-I-R1转变为T1-I- R1，再通过简单的几何计算得到路径为：25.033 25≈25.033。

③图5中T1-（EH线段上的某点K）-（EI线段上的某点O）-R1路线。

此时需要考虑是否桥接问题。

2.6 考虑桥接问题

根据DSH-590号TCL决议单80 °角规则（沟槽桥接规则）：如果V型沟槽顶角大于80 °其爬电距离应沿着槽的轮廓进行绘制（图6）；如果V型沟槽顶角小于等于80 °，且开口宽度大于短接尺寸“X”，其爬电距离应沿着槽的轮廓进行绘制，但槽底用短接尺寸为“X”的连接跨接（图7）[3]。（2级污染等级X=1.0 mm和3级污染等级X=1.5 mm）。

由于标准IEC 60664-1和TCL决议590中只是对平面桥接进行定义，而此处可能涉及空间桥接的最短爬电距离问题，所以笔者认为简单的以面面夹角∠H1EH2<80 °即认为满足桥接条件是不合理的。

由模型可知爬电距离的最小路径必定存在，所以我们先假设通过空间桥接AB（图9中）最短路径在T1-KA-B-R1（图9中路线）取得，最后我们再验证最短路径时，在跨接点已知的情况下，如果不桥接所形成的最短路径夹角是否＜80 °，如果夹角＜80 °，则满足标准和TCL决议中平面桥接角＜80 °的要求，如果不满足则需要剔除部分角度对应的路径。

2.7 分析模型并建立数学模型

对模型中关键的桥接角进行简单的分解（图8，图9，图10，图11）。

图4 样品的三维模型

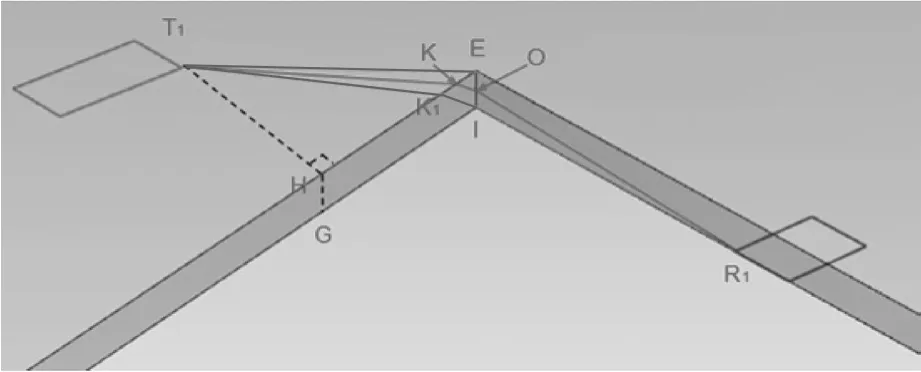
图5 T1到R1的爬电距离3种可能的路径模型

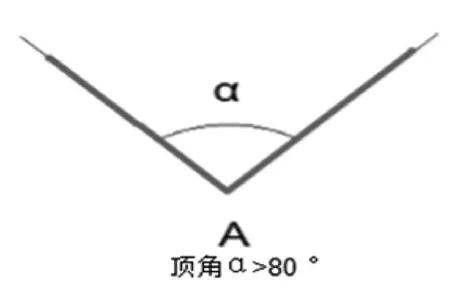
图6 V型沟槽顶角＞80 °时的爬电路径

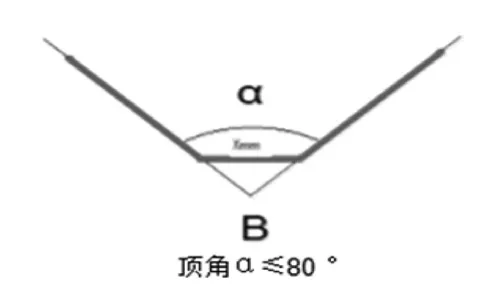
图7 V型沟槽顶角≤80 °时的爬电路径

图 8 样品桥接角局部实物照片

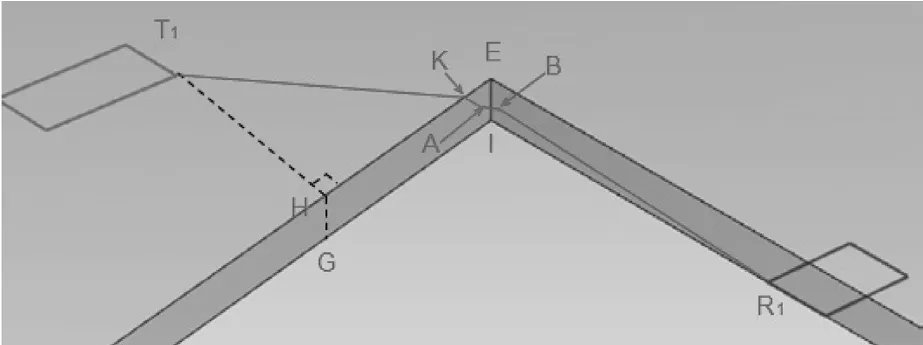
图9 样品桥接角局部模型

假设：在桥接的情况下取得爬电距离最小值，T1-KA-B-R1。

对于任意的桥接路线AB必能做出一个（H1-H2-H3-H4辅助平面）垂直于（H3-H4-R1底面）。

对图10分别沿着H-H1，H1-H3,H2-H4展开得到图11。

做AB在经过A点且平行于底面（水平平面GIR1）的辅助平面A-F-D。即AD为AB在水平辅助平面A-F-D的投影，A为辅助平面与H1H3的交点，F为辅助平面与EI的交点，D为辅助平面与H2H4的交点。

现在已知：AB=1 mm（2级污染等级X=AB=1.0 mm，3级污染等级X=1.5 mm，1.5 mm的路线有变化后面再讨论），T1H，GI，HG，IR1以及θ为定值（可以直接测量得到），求爬电距离最小值T1-K-A-B-R1。

最短路径可以分段求解T1-K-A-B-R1=T1-K+KA+AB+BR1，AB已知，由展开图11可知两点之间线段最短，即T1-K-A为一条直线时取得最短距离T1A。

设AH1为变量（0≤AH1≤HG）；角度∠BAD为变量α，由于要取得最短路径所以0 °≤α≤90 °；∠FAD为变量β，由三角形内角和为180 °可知：0 °≤β≤180-θ °；∠FDA为γ，γ=180-θ-β。

最短路径为：

式中：

T1A—为图11中T1到A的线段路径；

AB—为图11中A到B的线段路径；

BR1—为图11中B到R1的线段路径。

由勾股定理可知：

式中：

T1H—为图11中T1到H的线段路径；

AH1—为图11中A到H1的线段路径；

GH3—为图11中G到H3的线段路径；

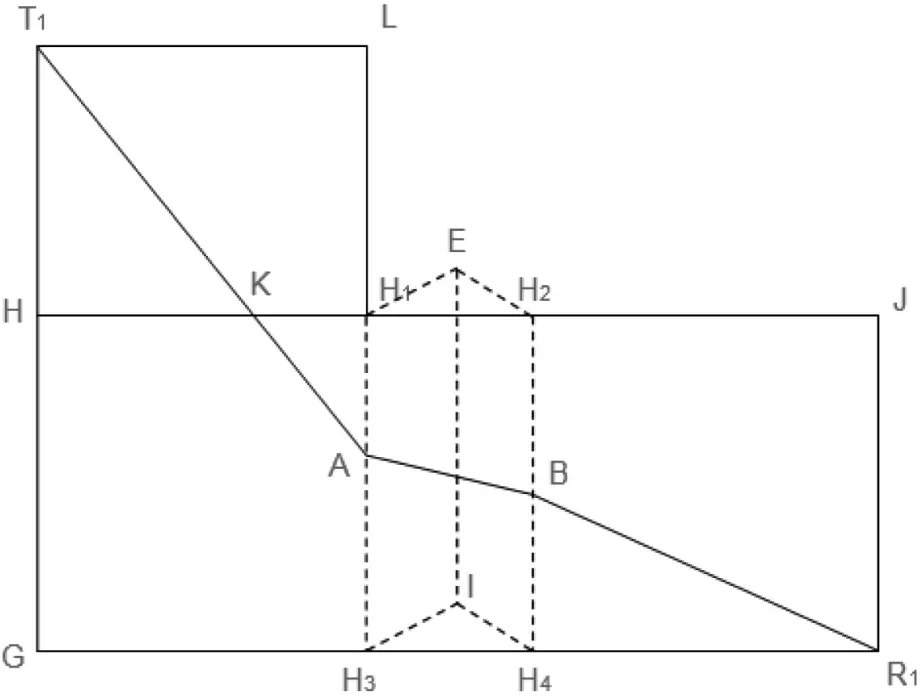
图11 桥接角展开图

BH4—为图11中B到H4的线段路径；

H4R1—为图11中H4到R1的线段路径。

式中：

GI—均为图10中的G到I线段路径；

AF—均为图10中的A到F线段路径；

HG—均为图10中的H到G线段路径；

DB—均为图10中的D到B线段路径；

IR1—均为图10中的I到R1线段路径

FD—均为图10中的F到D线段路径。

又由三角形AFD满足正弦定理：

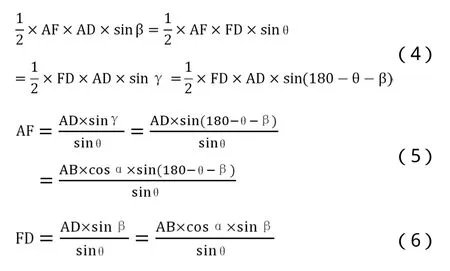
式中：

AD—为图10中A到D的的线段路径；

θ，β，γ—均为图10中的角度。

公式（3）化解为公式（7）

2.8 通过EXCEL辅助计算

在2.7的公式（7）中有3个变量α，β， AH1，通过EXCEL辅助计算。

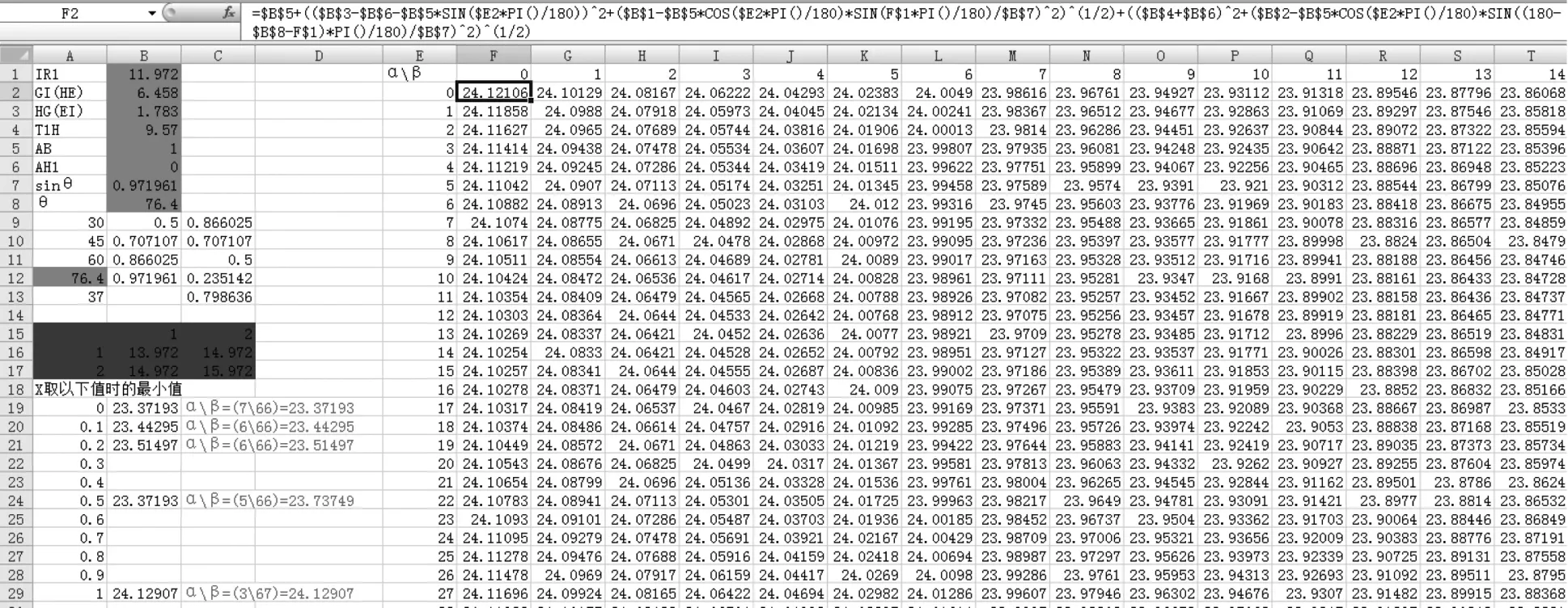
图12 通过EXCEL计算得到的T1-R1爬电距离最小值

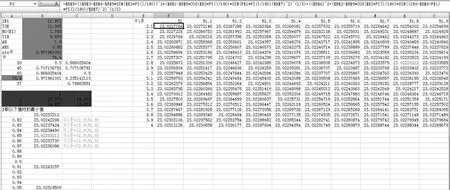
图13 不同污染等级的T1-R1爬电距离最小值

先取其中α，β两个角度做表格，找到AH1为定值时，任意角度的爬电距离最小值；又由于已知爬电距离必定存在最小值，再将AH1反复替换从最小取到最大值寻找规律，反复搜索表格中最小值，以及最小值取得的对应角度，得到T1-R1爬电距离最小值如（图12）在AH1为0，α=7 °，β=66 °时，取得爬电距离最小值为 23.37193≈23.372。

从结果可以看到路径3是明显小于路径1和路径2的值的。

2.9 计算步长的选取与结果的精确度

此时还应当对角度α，β和AH1尺寸进一步细化，计算步长选取0.1 °和0.01 mm精确度,此时取得最小值AH1为0，α=6.8 °，β=65.5 °时，取得爬电距离最小值为23.371 87≈23.372.从表1中可知：最短爬电距离到小数点后第四位才发生变化，二者数据相差只有0.000 06 mm，基本可以忽略，所以选取1 °和0.1 mm精确度已经足够满足要求。

表1 采用不同计算步长求得的最短爬电距离

图14 计算爬电距离最小值的JAVA代码

图15 通过代码计算得到的爬电距离最小值的结果

2.10 验证桥接角

最后还需要验证不桥接所形成的最短路径夹角是否＜80 °，如果夹角＜80 °，则满足标准和TCL决议中平面桥接角＜80 °的要求，此处问题又转化为了求易面直线和线段的最大夹角问题。

由于各个变量在最短路径的情况下均为已知量，可以建立向量坐标系，联立方程求解；也可以在模型上不断的穷举量取；均可证得此例中最短路径的情况下，若是不桥接所形成的最短路径夹角＜80 °（本文中就不再赘述具体证明过程）。

2.11 不同污染等级时的最短爬电距离

当污染等级为3级，AB=1.5 mm时，T1-T2和T2-T3之间路径分别小于1.5 mm，在爬电距离计算中直接跨接视为0，最短路径转化为T3-R1。同理可得最小值，但是最小值并不是在AH1为0时取得，取得最小值时AH1为0.85，α=2.8 °，β=51.8 °时，取得爬电距离最小值如（图13）为23.022 3≈23.022。

3 通过编程计算

2.7中的公式（7）也可以用编程进行辅助运算，可以更加节省时间，得到更加精确的结果，笔者使用JAVA语言辅助计算，相关环境配置此文不再赘述，具体代码如图14。

此代码由于步长太小，计算量过大，容易引起内存溢出，可以考虑变量分段计算，最后得到：当AH1为0，α=6.8 °，β=65.5 °时，爬电距离最小值的结果（如图15）=23.1873675670287≈ 23.372。

相比于通过EXCEL计算得到的结果更加精确，快捷。

4 总结

爬电距离与电气间隙的测量几乎涉及到所有类别的电气产品，测试方法和要求也仍在不断完善当中，但测量方法的核心仍应围绕路径本身，但是实际被测产品的多样性加大了测量难度，所以在遇到需要空间桥接或者类似的复杂电气间隙爬电距离问题时，引入三维建模，数学建模，利用EXCEL或编程运算是未来求解复杂的爬电距离和电气间隙最小值的一种值得参考的思路和方案。

同时文中提到的建模、利用EXCEL或简单编程计算路径的解决方案，在空间路径的测量方面有着非常实用的前景，适合一般工程技术人员在日常工作中去处理一些空间路径的相关问题，本文的介绍希望对广大读者有所帮助。