基于EPS系统传感器角度信号的游标算法研究

宋昌平 侯训波 孑L飞 李峰 郭力铭

摘要：EPS系统传感器输出的角度信号为PWM形式，可被ECU采样识别，按基本算法来测量角度，将耗费大量ECU运算资源，影响运算效率。针对传感器所输出的角度信号开展研究，经分析信号特性、角差规律等，总结角度测量的游标算法和游标可信度的评价方法，其优势较为明显。以仿真验证方式，发现当方向盘角速度较高时，游标算法所测量角度结果不可信，甚至错误。据此，提出附加角速度判断条件，确定游标算法所测量角度结果是否有效，为另一种跟随算法提供正确且有效的角度基准。

关键词：EPS系统;角度传感器;角度测量;游标算法;游标可信度;角速度

中图分类号：U463.4 文献标识码：A 文章编号：1005-2550（ 2021） 06-0061-07 Research of Vernier Algorithm Based on Sensor Angle Signal in

EPS System

SONG Chang-ping 1， HOU Xun_b0 2， KONG Fei 3， 11 Feng 4， GUO Li-ming 2 （1. Dalian Vocational Technical College， Dalian 116037， China; 2. Dalian Innovation PartsManufacturing Company， Dalian 116620， China; 3.Jiangxi ISUZU Motors Co.，Ltd. Nanchang

330103， China; 4. Foshan Factory Beiqi Foton Motor Co.，Ltd. Foshan 528137， China）

Abstract： The angle signal output by the sensor of EPS system is in the PWM form， whichcan be sampled and identified by ECU. To measure the angle according to the basic algorithmwill consume a lot of ECU computing resources and affect the computing efficiency. The anglesignal output by the sensor is studied. By analyzing the signal characteristics and the law ofangle difference， the vernier algorithm of angle measurement and the evaluation method ofthe vernier reserve are summarized， which have obvious advantages. It is found that when thesteering wheel angular velocity is high， the angle measured by the vermer algorithm is notcredible， or even wrong. On this basis， additional angular velocity judgment conditions areproposed to determine whether the angle measured by the vernier algorithm is valid or not，and to provide a correct and effective angle reference for another following algorithm.

Key Words： Electric Power Steering System（EPS）; Angle Sensor; Angle Measurement;Vernier Algorithm; Vernier Reserve; Angular Velocity

1 前言

現代汽车配装电动助力转向系统（简称：EPS系统）已非常普及。角度传感器作为EPS系统的核心部件之一，直接影响系统性能，其角度信号对于实现主动回正等功能又是必不可少的[1]，甚至高端车辆的线控转向系统采用了双转角传感器[2-3]，可见其重要程度。此外ESP等底盘电控系统也需要与EPS共享角度信号，实现底盘一体化控制，转角传感器也是关键[4]。目前EPS系统传感器较多地采用了非接触式，其输出角度信号也采用了占空比PWM形式，具有较强抗干扰能力，被广泛应用。鉴于此，本文针对Hella传感器的角度信号，开展角度测量的算法研究，并分析游标算法的角差规律及游标可信度与角速度的关联性。

2 传感器工作原理和角度信号基本特性

本文研究的EPS系统传感器为Hella非接触交变电磁感应式的扭矩转角传感器，如图1所示，它除了能输出扭矩主信号T1和副信号T2，还能输出与角度相关的主信号P和副信号S，均为PWM占空比形式的信号，这些信号是经过传感器内置IC计算处理后成为可用的信号，再传输到EPS系统控制器（简称ECU），参与系统工作[5]。其中PWM_Py/Sy/Tly/T2y是未经处理前的角度主信号/角度副信号，扭矩主信号/扭矩副信号，也是传感器的原始信号，它们是由分别固连在输入轴和输出轴上的2个转子，与PCB板上的预埋线圈和3个芯片配合产生的，当2个转子随输入轴和输出轴转动时，由固定位置的预埋线圈可感应转子角度变化。

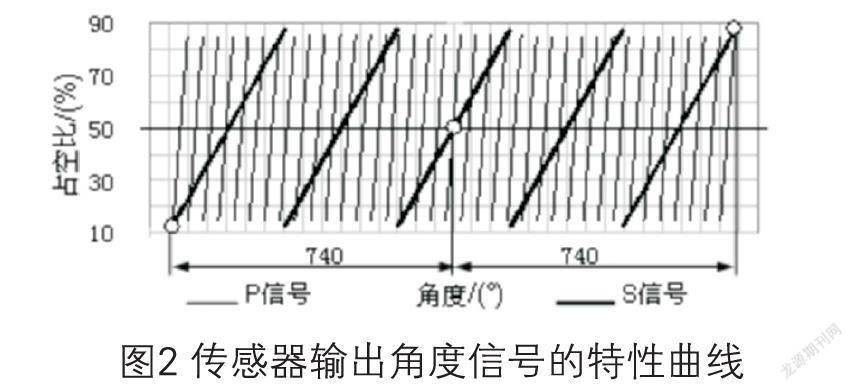
为使传感器能准确且可靠地被EPS系统应用，来测量方向盘转角，需对其原始角度信号进行标定。当不同传感器被EPS系统装配后，其原始角度信号的特性曲线的相对角位置关系是随机被固定的，没有统一基准，此时的原始角度信号若直接输出，则是不可用的。经标定后，由传感器内置IC建立虚拟的PWM_P和PWM—S信号与原始角度信号对应，此时输出则为新构建的有统一基准的信号，其特性曲线如图2所示[5]。其中PWM—P信号为40°一个循环，共37个周期，PWM__S信号为296°一个循环，共5个周期，综合角度范围为14800，且二种信号每个循环的有效PWM数值范围均为12.5%-87.5%。

如图2所示的特性曲线，可以理解为任意一段1480°角度范围内的曲线，若将其首尾相连，则是循环重复的。在任何一段14800范围内，若划分0-1480°角度刻度，则任意角度点均存在唯一的P信号值PWM—P和S信号值PWM—S组合与其对应，即可表示为θ=f（PWM▁P，PWM_S），若超出了14800范围，则会出现重复信号组合。因此，ECU通过相应算法所识别的角度为相对角度，仅在1480°范围内有效。

3 角度测量的基本算法

角度测量是由ECU对传感器输出信号进行采样，并将采样值PWM_P和PWM_S按相应算法计算，获得角度值的过程。

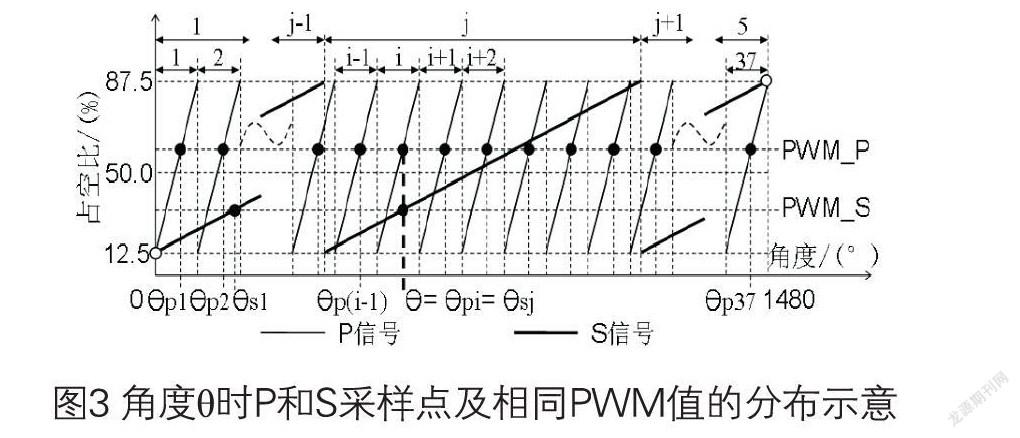
如图2所示，将PWM_P=PWM_S=12.5%特征点作为基准零点，向右1480°范围内展开，又将P信号各特性区段编号为i（ i=l、2、…、37），S信号各特性区段编号为j （j=l、…、5）。设当前角度O时，传感器输出且被ECU采样获得的角度信号值为PWM—P和PWM—S，按2种信号各自对应的角度θpi，和θsj，如图3所示分别为：θp1、θp2…θp37和θs1、…、θR5。与采样点相同PWM值所对应角度θp1，和θsj的表达式分别如下：θpi=（i-l）×40°+40°×（PWM_P- 12.5%） /75%（1）i=l、2、…、36、37θsj=（j-1）×296°+296°×（PWM_ S-12.5%）/75%（2）j=l、2、3、4、5

3.1 理想状态的角度测量基本算法

理想状态是指传感器所输出的角度信号未受到任何因素的影响。当在任意角度θ下，理想状态所对应PWM_P和PWM_S的唯一组合，都存在唯一角度点θ=θpi=θsj现象，由此可得理想状态的角度测量基本算法如下：θ=LOOKUP（0，θpi - θsj，θpi）（3）i=1、2、.，、36、37，j=1、2、3、4、5

3.2 实际状态的角度测量基本算法

实际状态是指传感器所输出的角度信号受到一些因素的影响，将产生信号采样误差。如：传感器内置磁性小齿轮的啮合存在间隙，其它机械匹配件之间也存在间隙，甚至振动以及采样电路等因素都会造成信号采样误差。为尽量降低这些误差对角度测量有效性的影响，需将PWM—P和PWM—S的误差分别对待。由于P信号受影响因素较少，以此为角度测量算法的基础，可增强测量准确度，这样PWM_P误差将成为实际状态的角度测量精度的主要影响因素;而由于S信号受影响因素较多，在实际状态下的角度测量算法中，作为辅助信号仅被过渡计算所采用，来判断置信区间范围，依此来评价可信度（又称：游标可信度）Vres（Vemier reserve）。

根据以上描述，以示例方式来展示其中规律，将归纳出实际状态的角度测量基本算法。例如：当前角度仍为O=385°时，在实际状态下仍有PWM—P=59.375%采样值，而S信号采样值，为模拟实际状态，则刻意按一系列偏差给出，其每组组合后仍分别由ECU按式（1）和式（2）计算角度θpi和θsj对应值，设△θij=θpi一θsj，再计算并搜寻其中I△θij|最小值：|△θij|min，以及与|△θij|min对应的△θij值：Aθij-m°由此可发现一个规律：当PWM—P=59.375%时，为能准确获得θ=385°计算值，需保证PWM_S=35.051±1.014%内，即θsj= 385±4°，此时角度偏差值4°就成为S信号所允许最大偏差角度，这也是对传感器输出S信号所有因素引起的总偏差要求。该规律适用于任何PWM—P采样值时，所对应理想状态下PWM—S值，其偏差符合±1.014%时，就可认为θ=θpi.是可信的，依此，实际状态的角度测量算法表达式为：

实际状态的基本算法可信度表达式为：

Vres=[100×（1-l△θij|min/4°）]%

（5）

4 角度測量的游标算法

在角度测量基本算法中，需ECU实时对传感器角度信号采样，来计算角度θpi，和θsj共185个对应值，同时还要统计I△θij-|θpi-θsj|最小值|△θij|min，并搜寻对应|△θij|min的θpi值，来确定当前被测量角度。该算法过程将耗费ECU大量的运算资源，会影响效率，甚至影响正常工作。因此，角度测量游标算法是经改进并简化后的算法，较适于被推广应用。

4.1 角差规律分析

当检测到的角度差值与标准角度差值，存在一一对应关系时，就符合游标算法原理[6]。设当前角度θ值对应角度信号采样值为：PWM_P和PWM—S，其中PWM—P采样值在37个区段中，对应同角位置上的S信号点定义为Sj-i，同时Sj-i信号点所在j区段的PWM_S=12.5%点距该Sj-i信号点角度定义为θsji;定义PWM_P采样点距i区段PWM-P=12.5%点的角度为θp，在各P信号区段中角度θp均相同，

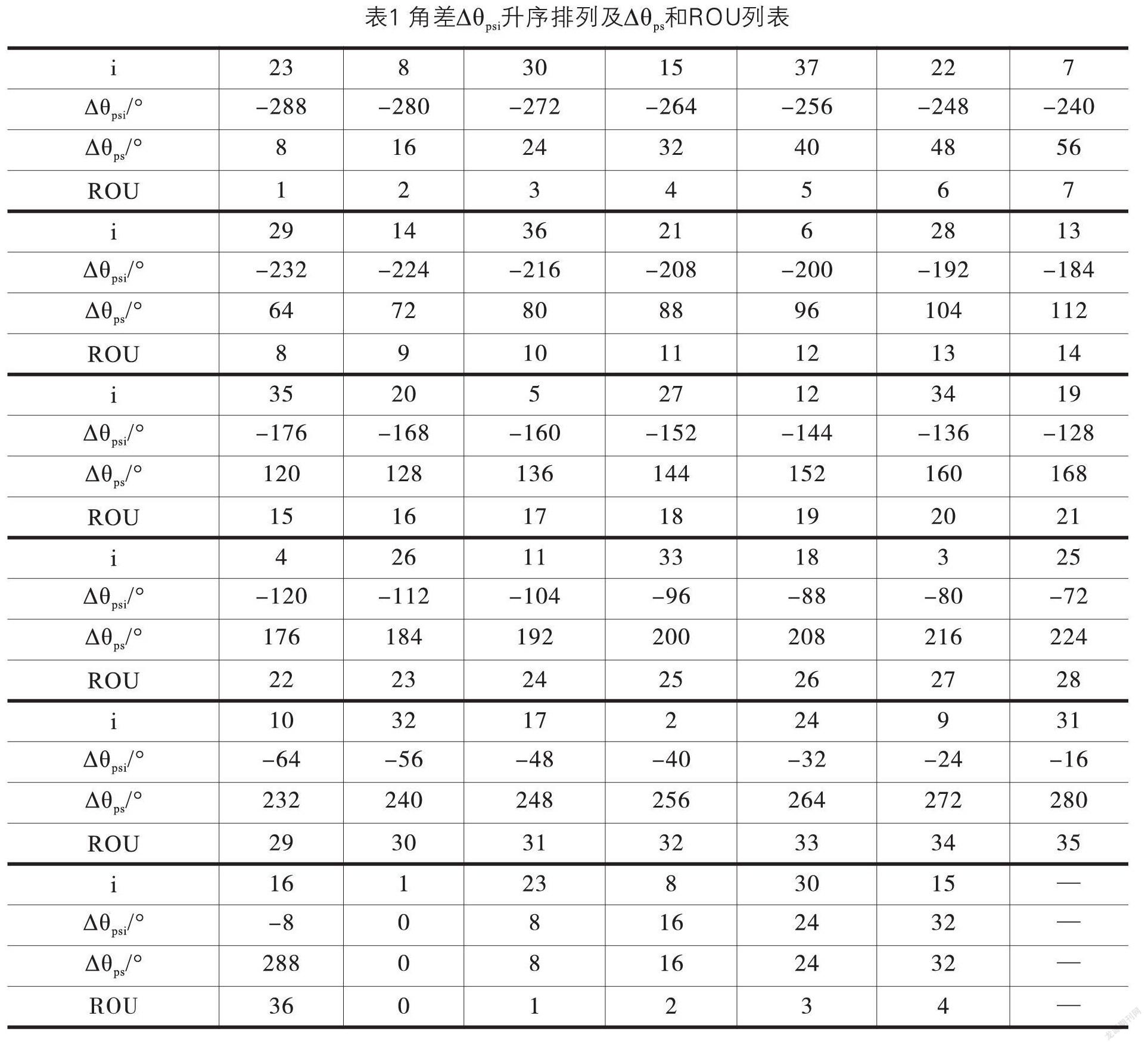
设角差△θpsi=θp一θsj-i，根据图4所示的规律，可列出37个i与△θpsi数组，再将角差△θpsi按升序排列，所对应的P信号区段编号i也随之对应。由此可以发现，在编号i=8、15、23、30四个P信号区段中，每段都会出现S信号循环切换现象，使△θpsi出现二种不同角差值，其它编号中的角差值是恒定的;还发现：将在编号i=8、15、23、30所对应角差值中负值，分别加上S信号周期角度2960后，四段编号中的角差值就统一了，依此方法将所有角差等效转化，即可使转化后角差值与编号i形成唯一的对应关系，如表1所示。对角差△θpsi进行逻辑转化为△θps，也列入表1中，其逻辑算法如下：

（6）

对表1中△θps观察发现，每间隔80就变换新编号i值。若将△θps实际值对比表中最接近的标准值，并全部归属于该标准值上，则使实际值具有明确的归属性且是唯一的。依此思路，将△θps值除以80后，四舍五入取整处理，即可达到上述目的。取整数代号定义为ROU，其结果列入表1中，ROU表达式为：

ROU=ROUND（△θps/8°，0）

（7）

从表1中还可以看出，P信号区段编号i与角差转化后取整数ROU，具备由ROU—i的唯一对应关系，并且取整数ROU还具备±40偏差的融合能力。如：实际状态下的S信号可能存在一定偏差，会引起△θpsi，和△θps产生同量偏差，这些偏差均被控制在±4°之内，最终再被取整处理后，都归属于表1中的标准ROU整数。

4.2 角度测量游标算法

在实际状态下，设当前角度θ值对应角度信号采样值为：PWM_P和PWM_S，采样点所处区段编号仍分别为i和j。按本文序号4.1中定义的P信号角度θp和S信号角度θsj-i.有如下计算表达式：

根据实际状态下所计算的角度θp和θsj-i，可得实际角差△θpsi=θp-θsj-i再按式（6）和式（7），最终可得ROU整数，参照表1中ROU→i的对应关系，将确定当前角度θ所处P信号区段编号i，由此可计算角度e值，它们的算法表达式如下：

P信号区段编号i查表的表达式：

i=LOOKUP（ROU，[ROU→i]，i）

（9）

式中，[ROU—i]表示由表1中归纳出ROU与i的对应关系数组表。

角度θ计算表达式：

θ=（i-1）×4°+θp

（10）

角度测量游标算法由式（6）、（7）、（8）、（9）和（10）组成，其中ROU与对应关系，需以数组表形式存储于ECU中，便于查表获得i值。

实际状态的游标可信度表达式为：

（11）

5 算法验证及改进

经验证，在理想状态下，角度测量的游标算法与基本算法所得结果完全吻合。而在在实际状态下，当被测角度处于i编号为1、8、15、23、30、37这些特殊区段之外时，经验证两种算法所得结果也完全吻合。针对被测角度处于典型的特殊区段时，在实际状态下的验证结果进行分析，显示出此二种算法均存在异常情况，需实施改进。

5.1 基本算法改进

当前被测角度在0°和1480°两个循环节点附近，若出现S信号误差，会引起S信号采样点所对应的P信号区段编号i大幅度突变，同时也引起实际状态的基本算法中最小角差绝对值|△θij|min≥4°现象。因此实际状态的基本算法式（4）需增加补充条件，修改为如下2个表达式来组成：

（13）

同时，还需将实际状态基本算法可信度的式（5）修改为如下表达式：

注：式（14）运算之前，必须先执行式（13）将角度θ值求解完成后，再对最小角差绝对值I△θij|min重新赋值，并计算Vres。

5.2 游标算法改进

当前被测角度在P信号区段编号i=1时，且S信号出现负向偏差时，则无法计算角度O值，并出现ROU=37现象。因此，需针对角度测量游标算法中数组表[ROU→i]进行改进，其修改数组表如下：

6 游标算法与角速度

角度传感器被装配到EPS系统中，通常标定后可信度也是按游标可信度式（11）进行计算评价，在实际产品静态检测中，通常Vres都达到了62.5%以上，说明S信号角度偏差均可控制在±1.50范围内。P信号代表角度测量精度，通常PWM_-P静态偏差为±0.03%，影响角度测量的静态精度为：±0.016°。

以上指标均在静态下进行评价，当EPS系统执行转向动作时，必然使传感器角度信号处于动态中，特别是方向盘转动角速度，对游标算法可信度Vres和角度测量精度的指标，将产生极大影响。

由于P信号频率为IOOOHz，S信号频率为200Hz，它们的信号周期不同。因此，当方向盘快速转动，在他们各自的信号周期内将产生角度误差，而不被角度信号所反映，其动态角度误差与角速度关系如图5所示：

对方向盘操作，人力极限转角速度为10000/s，按图5所示，P信号角度误差为±1°，S信号为±5°。因此，选定P信号为主角度信号进行游标算法角度测量，是较可靠的，其角度测量的动态精度为±1°。

角度测量是根据1ms为周期的采样值：PWM_P和PWM—S，再通过游标算法来获得测量角度，但由于二种信号频率不同，其中P信号每更新5次，S信号才更新1次，这样就会引起可信度Vres降低，甚至出现角度测量错误。通常普通人转动方向盘的角速度极限为800°/s，当驾驶车辆时，受安全意识压力，一般不会超出600°/s，以此为例，利用可信度来分析角速度对游标算法的影响，如图

如图8和图9所示，可以看出，当角速度为800°/s时，游标算法的测量角度结果是不可信的，若角速度再提高，则会更频繁地出现测量角度与实际角度不符，可信度Vres出現降至0%再提升的现象，这些测量结果均不可信。

如图6和图7所示，当角速度为600°/s时，未出现上述错误，其角度测量结果与实际角度是基本吻合的，但可信度下降至2.50%，也有一定的测量风险。当角速度较高时，也就相当于采样时刻的P信号和S信号有机会产生较大的相对角度误差，如图10所示，由此引起角度误差超过了临界极限时，计算所输出的角度就变得不稳定[7]。在EPS系统实际工作中，需设定可信度Vres≥25%最低限值，符合该限值要求的角度测量结果才允许被ECU应用，否则本次测量结果将被禁用。

如图10所示，在传感器角度信号已存在最大静态P和S相对角度误差1.5°及当前可信度Vres=62.5%的情况下，随着方向盘转动角速度的提高，会出现以下三种情况。第一种：当角速度小于375°/s时，Vres均大于25%，所测量角度是可信的，可被ECU应用;第二种：当角速度大于3750/s而小于8750/s时，Vres均小于25%，所测量角度是不可信的，将被ECU禁用;第三种：当角速度大于875°/s时，Vres也大于25%，但所测量角度是错误的，也将被ECU禁用。

针对第一和第三种情况，均出现了Vres大于25%的现象，还需角速度估测值作为附加判断条件，来确定角度测量结果是否有效。其判断关系式如下：

式中，w一角速度，TRUE-有效测量，FLASE-无效测量。

当游标算法所测量角度由式（ 15）判断为无效时，不能被EPS系统应用，将由另一种跟随算法所测量角度来提供，两种算法需配合使用。跟随算法是根据游标算法所确定的角度基准，以独立P信号采样值进行增量式的角度测量[8]，避免了角速度对测量的影响，同时也可扩展角度测量范围。

7 结束语

游标算法是利用EPS系统传感器角度信号，通过ECU对相对转向角度进行测量的一种方法，仅在0-1480°范围内有效。当方向盘角速度较高时，游标算法会出现角度测量错误，将引起EPS系统回正等功能被错误启动，而造成转向不平顺现象。本文提出了在游标算法中附加角速度条件，来确定所测量角度是否有效。在EPS系统实际应用中，因游标算法存在上述不足，需与另一种跟随算法配合使用。

参考文献：

[1]那少聃.用于EPS的非接触电磁感应式角度传感器研究[D].哈尔滨：东北林业大学，2015： 1-5.

[2]何磊，馬伯祥，宗长富，线控转向汽车转向盘转角传感器的容错控制策略[J]汽车工程，2015，37（3）：327-330+345.

[3]陈俐，李雄，程小宣，等，汽车线控转向系统研究进展综述U].汽车技术，2018（7）：23-34.

[4]杨财，周艳霞，方向盘转角传感器研究进展[J]传感器与微系统，2007（ 11）：1-4.

[5]宋昌平，侯训波，刘晓文，等.EPS系统传感器角度信号静态标定及算法解析[J]汽车零部件，2021（ 5）：13-19.

[6]牛勃.非接触式方向盘转角检测算法的研究[D].哈尔滨：哈尔滨工业大学2015： 22-25.

[7]罗兰.盖迈希，基于游标原理的转向角度传感器运行期稳定性监测：中国，201880088362.7[P].2018-02-02：1-10.

[8]侯训波.基于传感器P信号实现EPS补偿控制策略和算法[J].汽车工程师，2020（ 6）：39-43.

专家推荐语

王坤

东风汽车集团技术中心

整车技术部副总工程师 高级工程师

本论文对基于EPS系统传感器角度信号的游标算法进行了详细的解析性研究，对单一的游标算法的特征和缺点进行了阐述，提出了需要追加组合算法的方案，并对组合算法的方案进行了分析扣阐述，提升了算法的容错率。本文的方法和思路对于自主开发的控制器传感器的信号处理提供了参考和借鉴，具有实用性和借鉴价值，有公开发表的价值。