基于结构方程模型分析林分空间结构对草本物种多样性的影响

曹小玉,李际平,赵文菲,委 霞,庞一凡

1 中南林业科技大学林学院,长沙 410004 2 南方森林资源经营与监测国家林业与草原局重点实验室, 长沙 410004

森林物种多样性直接影响着森林生态系统的结构稳定性和功能复杂性,维持森林物种多样性是培育健康、稳定、高效的森林生态系统的关键。草本层作为森林生态系统的重要组成部分,是影响森林生态系统乔木层幼苗更新、土壤层养分循环及防止水土流失的重要因素[1- 2]。然而林下草本物种多样性的维持在很大程度上依赖于乔木层林木的空间结构。这是因为上层乔木的空间结构直接决定着林下光照、土壤养分条件、土壤质地和凋落物性质的综合差异,进而显著地影响着林下草本的物种多样性[3- 5]。但林分空间结构包含众多指标,到底是林分水平空间结构对林下草本物种多样性影响大？还是垂直空间结构影响作用大？或是林木的竞争的态势影响作用大？目前尚不清楚,还有待进一步研究。因此研究林分空间结构对林下草本物种多样性的影响具有重要的理论意义。

目前,国内外学者已对影响森林生态系统林下植被物种多样性的因素及推动力进行了不少研究,但这方面的研究大都集中在林分非空间结构因子或环境因子对林下植被的影响[6- 8],而针对林分空间结构对林下植被物种多样性的研究却很少,朱光玉等基于湖南栎类天然林49块样地的实测数据,采用Pearson 相关分析和多元线性逐步回归分析研究了林分空间结构对林下灌木物种多样性的影响[9]。曹小玉等[2]采用灰色关联度分析方法研究了亚热带3种典型林分空间结构对林下草本物种多样性的影响。但这些一对一的直接关系研究,无法考察因变量的关系且缺少整体的视角,从而掩盖了林分空间结构影响林下草本物种多样性的真实机理[10-12]。因此,选择科学的统计方法来研究林分空间结构对林下草本物种多样性的影响来说至关重要。结构方程模型作为一种多变量统计方法,它能同时处理多个因变量[13- 16]。与传统的统计方法相比较,它不仅能揭示各影响因子之间的相互关系及影响强度,而且能对整体模型的适配度进行检验,从而可以帮助我们更全面地了解林分空间结构对林下草本物种多样性影响的真实机理[17]。到目前为止,结构方程模型研究方法已在教育领域、心理学领域、经济管理领域得到了广泛应用[18- 20],其他学科领域的研究也很多,比如社会行为、职业意识等[21- 23]。然而它在林学领域的应用却比较少[24]。特别是在林分空间结构对林下草本物种多样性影响研究方面的应用还未看到。基于此,本文以针叶纯林、针阔混交林和常绿阔叶林为研究对象,基于56个样地的实测数据,用混交度和角尺度表征林分水平空间结构,用林层指数和开敞度表征林分的垂直空间结构,用Hegyi竞争指数表征林木的竞争态势,采用结构方程模型研究林分空间结构对林下草本物种多样性的影响。试图通过分析林分空间结构对林下草本物种多样性的影响关系,揭示林分水平空间结构、垂直空间结构和林木竞争态势对林下草本物种多样性变异的相对重要性,以为维持或改善林下草本物种多样性提供结构化经营建议。

1 材料与方法

1.1 研究区概况

平江县位于湖南省东北部。地处113°11′—114°9′E,23°25′—29°6′N。全县土地总面积约41.14万hm2,其中林地面积约28.80万hm2,全县森林覆盖率64%。是湖南省的重点林业县。县境气候属大陆性季风气候区,东亚热带向北亚热带过渡气候带。年平均气温16.8℃,年积温6185.3℃,年平均降水量1450.8 mm,雨量和水热充足,适宜多种树木生长。

1.2 数据来源

2019年7—8月份,采取典型取样法分别在湖南省平江县福寿林场和芦头林场,选择立地条件基本一致的针叶纯林、针阔混交林和常绿阔叶林(表1)分别设置了16块、19块和22块20 m×30 m的矩形样地,一共56块样地。采用相邻网格法将每块样地分割6个10 m×10m的小样方作为乔木层调查单元,调查因子为小样方内每株树木的树种、相对坐标(x,y)、胸径、树高、平均冠幅等基本测树因子。在每个样地四角和中心地带设置5个1 m×1 m草本层调查小样方,调查记录草本层的物种名称、物种数量、物种高度和盖度。

1.3 研究方法

1.3.1林分空间结构单元的确定

本文采用4株木法确定林分空间结构单元。为避免以边界木为对象木的相邻木落在样地之外从而影响林分空间结构指数的计算,在20 m×30 m样地四周设置了3 m的带状缓冲区以消除边界影响。

1.3.2空间结构指数的计算

本文采用林分空间结构指数混交度、角尺度、林层指数、开敞度和Hegyi竞争指数5个林分空间结构指标来分析林分的空间结构。混交度用来反应林分树种隔离程度[25],角尺度用来映林分林木的水平空间分布格局[26],林层指数用来反映林分的林层多样性[27],开敞度用来反映林分林木的透光条件[28],Hegyi竞争指数用来反映林分林木的竞争态势[29]。

1.3.3物种多样性指标的计算

本文采用物种丰富度(S)、物种多样性指数和均匀度指数来分析林下草本物种多样性水平。其计算公式如下：

(1)

Simpson均匀性指数

(2)

Shannon-Wiener多样性指数

(3)

Pielou均匀度指数

(4)

式中,pi为草本第i种的个体数占所有种的个体总数的比例,S为所在样地内草本物种种类的总数。

1.3.4结构方程模型的构建

结构方程模型包括测量模型和结构模型两部分。测量模型是建立潜变量(无法观测变量)与外显变量(观测变量)之间关系的模型,其表达公式如下：

X=Λxξ+δY=Λyη+ε

(5)

式中：X为外源指标组成的向量,Y为内生指标组成的向量；ξ为外源潜变量组成的向量,η内生潜变量组成的向量。Λx是外源指标在外源潜变量上的因子负荷矩阵,即为反映外源指标与外源潜变量之间关系强弱程度的系数矩阵；Λy是内生指标在内生潜变量上的因子负荷矩阵,即为反映内生指标与内生潜变量之间关系强弱程度的系数矩阵；δ和ε为外源指标与内生指标的测量误差。

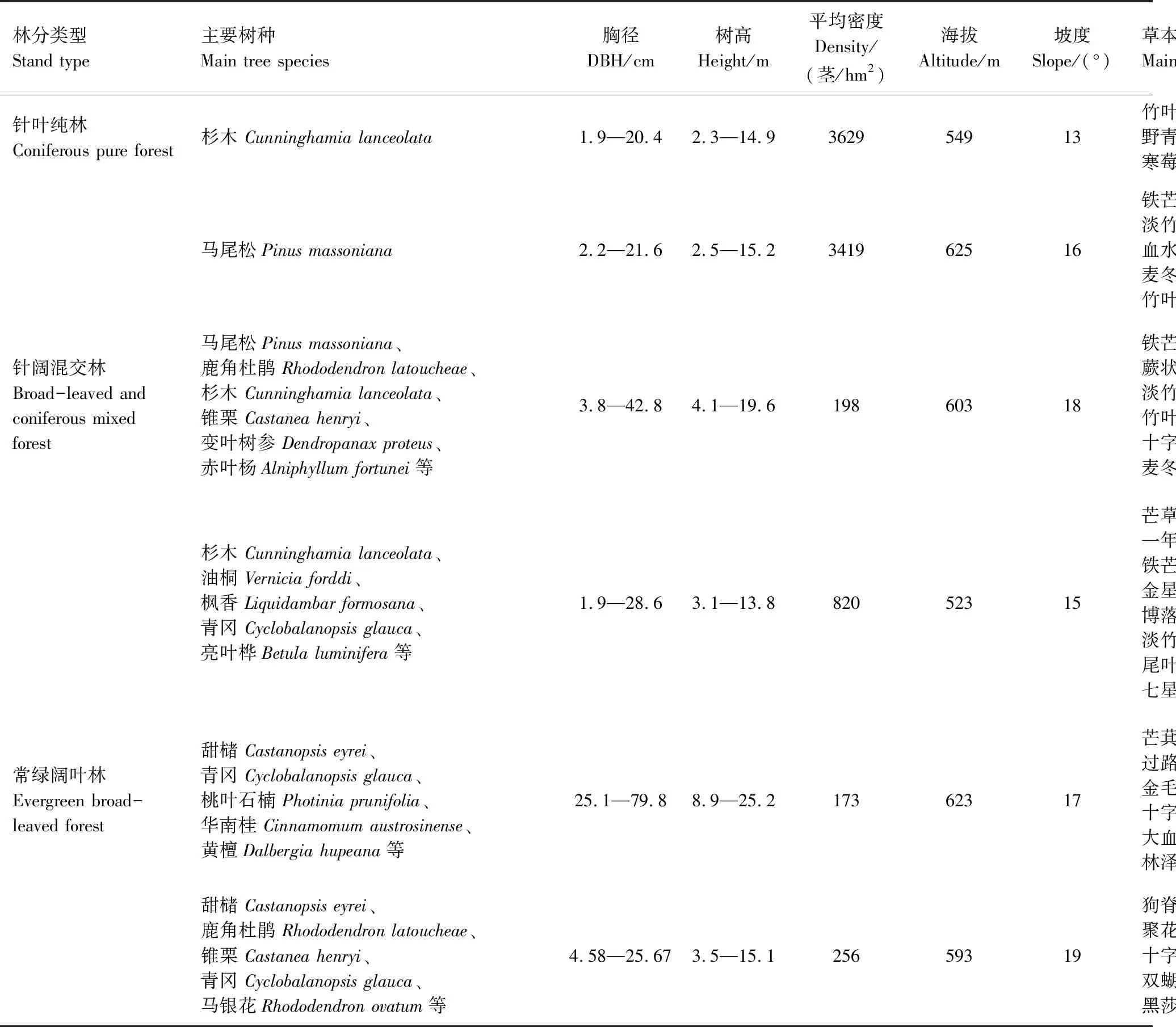
表1 各林分类型基本情况

结构模型是反映潜变量间因果关系的模型,其表达公式如下：

η=Βη+Γξ+ζ

(6)

式中：η为内生潜变量,Β为内生潜变量之间关系的结构系数矩阵；Γ为内生潜变量与外源潜变量之间关系的结构系数矩阵,ξ为外源潜变量；ζ为结构模型中干扰因素或残差值。

本研究在构建结构方程模型前,用Z-score方法对原始数据进行标准化处理,并利用方差膨胀因子(VIF)检验法删去了存在多重共性的变量。最终将林分垂直空间结构、林分水平空间结构作为外源潜变量,将角尺度和混交度作为林分水平空间结构的可测变量,将林层指数和开敞度作为垂直空间结构的可测变量。将草本物种多样性指数和草本物种均匀性指数作为内生潜变量,将草本Simpson多样性指数和Shannon-Wienner多样性指数作为草本物种多样性指数的可测变量,将草本Simpon均匀性指数 和Pielou均匀性指数作为草本物种均匀性指数的可测变量,并将将草本物种丰富度和林木竞争指数作为独立变量加入模型,构建了林分空间结构对林下草本物种多样性影响的概念模型(见图1)。

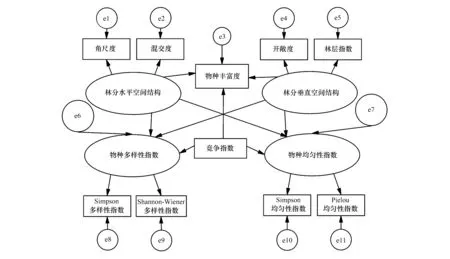
图1 林分空间结构对林下草本物种多样性影响的概念模型Fig.1 Conceptual model representing hypothesized relationships between stand spatial structure and herbaceous species diversity

1.3.5模型的适配度检验

为了确定最佳结构方程模型,本研究采用绝对适配统计量卡方自由度比χ2/df(Chi square degrees of freedom)、绝对适配度统计量适配度指数(goodness-of-fit index,GFI)和标准化残差均方和平方根(standardized root mean square residual,SRMR)对模型进行适配度检验。χ2/df介于1—3之间表示模型适配度良好。GFI的数值介于0—1间,其数值愈接近1,表示模型的适配度愈佳,一般的判别标准为GFI值大于0.90,表示模型的路径图与实际数据有良好的适配度。SRMR值介于0—1间,其数值愈大表示模型的适配度愈差,其值为0时,表示模型有完美的适配度,一般而言,模型适配度可接受的范围为其值在0.05以下。通过比较结构方程模型的χ2/df、 CFI 和 SRMR 的值,可以确定适配度最佳的模型。结构方程模型的构建及检验均使用AMOS 24.0完成。

2 结果与分析

2.1 林分空间结构

从表1可以看出研究区不同森林类型的林分混交度为0.116—0.7875,差异显著,变异系数为44.984%,平均混交度为0.4466,接近中度混交,说明林分混交度较好,树种隔离程度较优。角尺度为0.3098—0.39571,差异较小,变异系数为5.794%,平均角尺度为0.3538,接近随机分布状态,是比较理想的分布状态。竞争指数为3.5709—8.1469,差异较大,变异系数为23.279%,平均竞争指数为5.7701。林层指数为0.2261—0.7052,差异显著,变异系数为32.563%,平均林层指数为0.4445,与参照木不在同一林层的邻近木株数接近邻近木总株数的一半,林分的垂直生长空间利用较好。开敞度为0.4102—1.2184,差异显著,变异系数为33.161%,平均开敞度为06706,林分的生长空间基本充足。

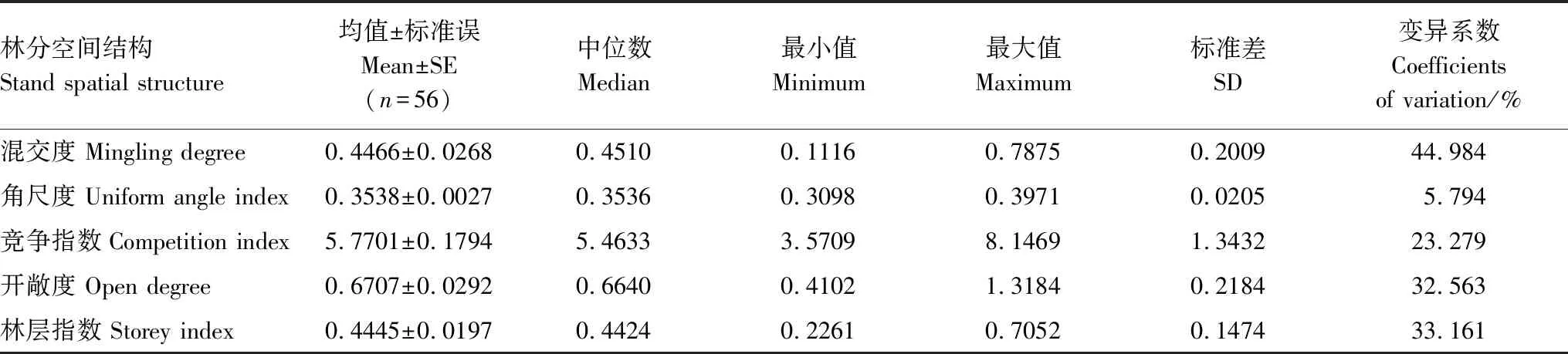
表2 林分空间结构指标基本特征统计量

2.2 草本物种多样性

从表2可以看出,研究区不同森林类型的林下草本物种丰富度、Simpson多样性指数、Shannon-Wiener多样性指数 、Simpson均匀性指数和Pielou均匀性指数差异显著,其值分别为 9—22、0.5392—0.9572、1.4164—3.2976、0.5806—0.9873和0.5367—0.9488。其中物种丰富度和Shannon-Wiener多样性指数变异程度较大,变异系数分别为31.358%和19.162%,其它3个指标变异程度较小,变异系数都在10%左右。

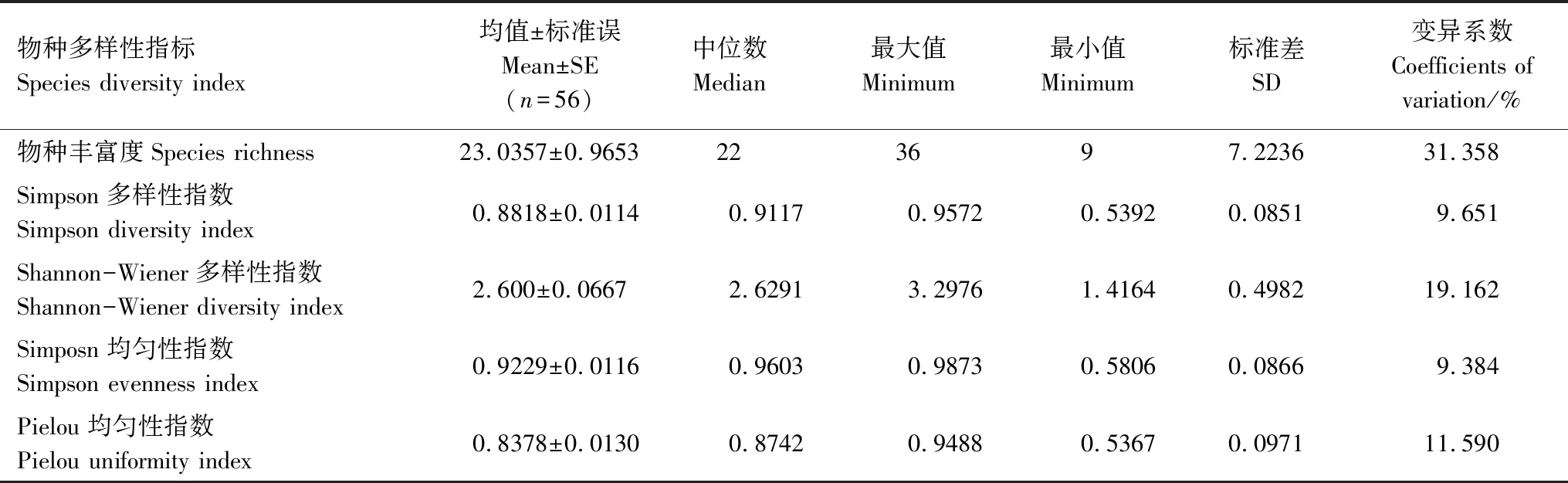
表3 草本物种多样性基本特征统计量

2.3 林分空间结构对林下草本物种多样性的影响

模型的适配度检验结果显示χ2/df的值为1.896、CFI为0.979、SRMR为0.039,说明构建的结构方程模型与数据的适配度较高,模型拟合基本理想。测量模型显示所有测量指标载荷均达到统计显著(表3)。其中在林分水平空间结构上载荷量最大的为混交度(0.80)；在林分垂直空间结构上载荷量最大的为开敞度(0.94)；在物种多样性指数上载荷量最大的为Shannon-Wiener多样性指数(0.95)；在物种均匀性指数上载荷量最大的为Pielou均匀度指数(0.95)。

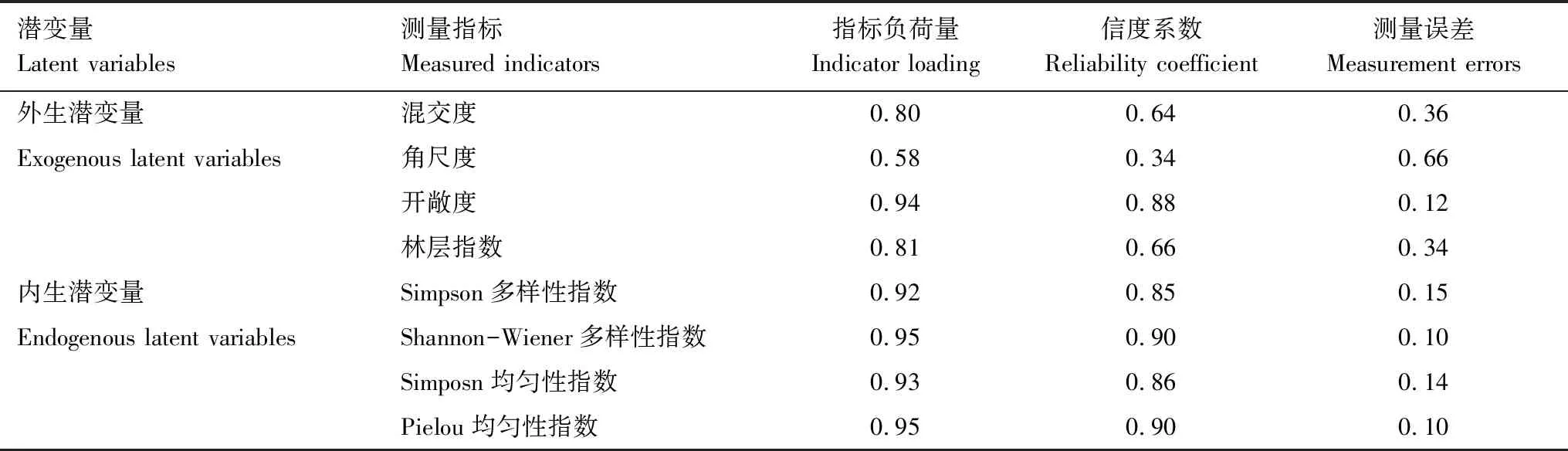
表4 结构方程模型中各测量指标因子载荷

而结构模型显示林分水平空间结构和林分垂直空间结构均对林下草本物种丰富度、物种多样性指数和物种均匀性指数均有显著的影响(P<0.01)(表3,图2)。其中林分水平空间结构对林下草本物种多样性指数和物种均匀性指数均有极显著影响(P<0.001),路径系数分别达到0.96和0.89；而对林下草本物种丰富度只有显著影响(P<0.01),路径系数为0.22。相比林分水平空间结构,林分垂直空间结构对林下草本物种丰富度和物种均匀性指数有极显著影响(P<0.001),路径系数分别达到0.86和0.43,而对林下草本物种多样性指数只达到显著影响(P<0.01),路径系数为0.16。林分竞争指数对林下草本丰富度、物种多样性指数和物种均匀性指数均为负的影响作用,其中林分竞争指数对林下草本物种丰富度和物种多样性指数均达到极显著影响(P<0.001),路径系数分别为-0.47和-0.30；而对林下草本物种均匀性指数未达到显著影响(P>0.05),路径系数为-0.04。

表5 基于结构方程模型林下草本物种多样性的总标准效应

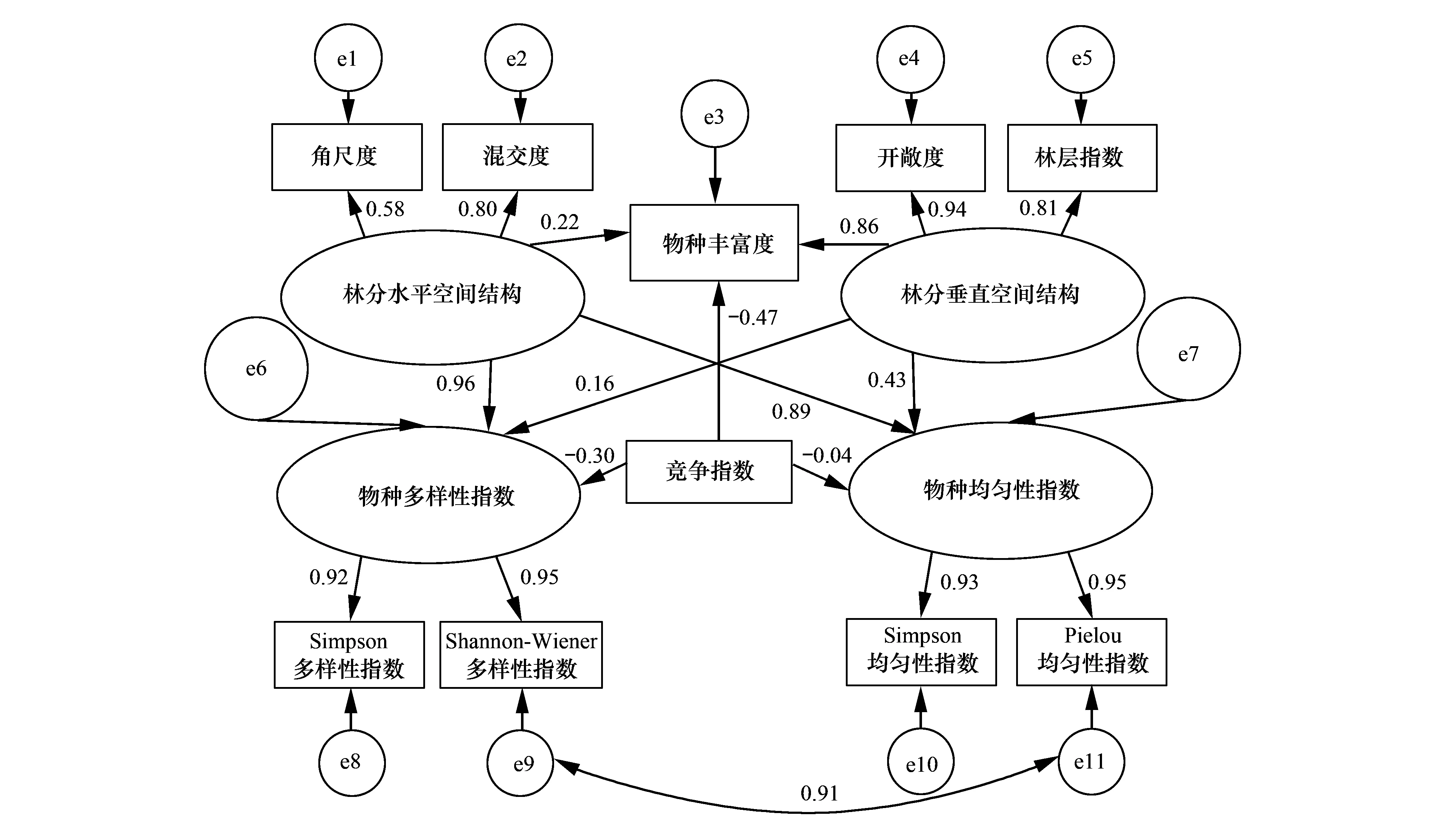
图2 林分空间结构影响林下草本物种多样性的路径图Fig.2 Final results of full model for relationships between stand spatial structure and herbaceous species diversity

3 讨论

探索林分结构与林下植被物种多样性的关系已成为林学领域研究的一个热点问题,了解林下植被物种多样性的驱动因素对揭示林下植被物种多样性的形成和维持机制意义重大[30-31],大量的研究表明,林分空间结构对林下草本物种多样性的影响,不仅归因于林分水平空间结构,还依赖于林分垂直空间结构和林木的竞争态势,但其对林下草本物种多样性的相对重要性仍不明确,值得进一步研究[32-33]。本研究用混交度和角尺度表征林分水平空间结构,用林层指数和开敞度表征林分的垂直空间结构,用Hegyi竞争指数表征林木的竞争态势,探讨了林分水平空间结构,垂直空间结构以及林木竞争态势对林下草本物种多样性的影响的相对重要性。研究结果显示林分水平空间结构极显著地影响林下草本的物种多样性指数和物种均匀性指数(P<0.001),这与前人朱光玉、黎芳等的研究结论基本一致。朱光玉等[9]研究发现湖南栎类天然次生林林下灌木的物种多样性和物种均匀性都随着乔木层林木混交度的变大而随之增大。黎芳等[34]研究也发现飞播马尾松林林下灌木和草本的Shannon-Wiener 指数都受乔木层林分角尺度和混交度的显著影响(P<0.05) 。这可能是表征林分水平空间结构的混交度和角尺度直接影响着林下草本生长的微环境和水平分布格局所致。一方面多树种混交的林分,各树种在生态位上相互抑制,降低了林木的竞争程度,为林下草本的生长释放了营养空间[35]；同时不同树种在地表积累的丰富凋落物和纵横交错、深浅不一的根系显著地增强了土壤养分的归还和循环能力,改善了林下草本生长的土壤条件[36]。另一方面,乔木层林木的水平分布格局(角尺度)直接影响着林内林窗面积的大小和位置,而林窗内草本的数量、种类及其分布的均匀程度均受林窗面积和位置的影响,研究发现小林窗内的草本层受灌木屏障作用较小,接受的光照强度适中,生长旺盛,而大林窗光照强度太大,林窗内水分减少,影响了草本对资源的利用效率,反倒不利于草本层的生长[37]。

研究结果显示林分垂直空间结构极显著地影响林下草本丰富度和物种均匀性指数(P<0.001)。这可能是表征林分垂直空间结构的林层指数和开敞度直接影响着林下光照、热量、水分、土壤、风速等一系列草本生长的环境[38]。一方面,乔木层的林木开敞度直接影响着林下有效光强度,从而在一定程度上决定着林下耐荫草本、需光量大的非耐荫草本及其普通草本的成活率,进而影响着林下草本的物种丰富[39]。另一方面,乔木层的林层结构决定着林下光斑位置和林木的蒸腾作用强度,枝繁叶茂、冠层重叠交错的林层结构,会使林分内光斑位置更均匀,林木的蒸腾作用更强。均匀的光斑位置会使林下草本的物种均匀度指数随之增加,较强的林木蒸腾作用会使林地内更易形成丰富的枯枝落叶,能增加土壤中的有机质和肥力,更有利于林下草本层的生长[40-41]。

研究也同时发现林分竞争指数对林下草本丰富度和物种多样性有极显著的负影响作用(P<0.001)。这可能是由于激烈的林木竞争会导致的林分营养空间和生活空间的不足,从而必然引起林下草本种内和种间的激烈竞争,导致林下草本物种丰富度和多样性减少。前人研究也发现,林木竞争主要发生在相邻木之间,表现为相邻木对竞争单元范围内光资源、土壤资源和水资源等的竞争,竞争水平高的林木存在排斥效应,加剧了林下草本在有限光照环境和水肥条件下的劣势地位,导致部分草本植物被竞争淘汰,从而使林下草本的物种多样性降低[42-43]。

从系统论的观点看,只有保持优良的林分空间结构,才能使森林生态系统功能得到较好的发挥,森林结构化经营与管理本质就是从复杂现象中探讨林分空间结构对林分功能的直接或间接影响关系,提出理想的林分空间结构模式,实现森林多功能经营[44]。自然森林是一个复杂的自然系统,描述林分空间结构对林分功能的影响关系时,不能单靠一对一的简单关系来直接描述,更要注重林分空间结构间的相互关系和林分空间结构影响林分多功能过程间的相互作用,并分析多个过程的影响因子和变化趋势,才能科学的揭示林分空间结构对林分功能的影响机理[45]。相比传统的统计方法,结构方程模型在解决生态系统耦合关系问题上具有强大能力和优势,它通过容易量化的可测变量来估计无法直接测量的潜变量,进而揭示潜变量的相互关系,并通过直接作用和间接作用描述这种相互关系,为揭示林分空间结构影响林分多功能的复杂关系提供独特的整体视角[46]。研究表明结构方程模型能够从整体上直观地反映林分空间结构对林下草本的物种多样性的影响。结构方程模型不仅定量描述了林分水平空间结构、林分垂直空间结构和林木竞争态势对林下草本物种丰富度、物种多样性和物种均匀性的影响,也直观地展现了其影响路径,整体上比较科学地揭示了林分空间结构对林下草本物种多样性的复杂作用。但结构方程模型对样本数量要求较高,在社会科学领域需要成百上千的样本数量,来提升模型的拟合度[47],因此,在后续研究中,需要继续增加研究样地的数量,以弥补样本数量不足的缺陷。

4 结论

林分的水平空间结构、林分垂直空间结构和林分林木竞争指数均对林下草本的物种多样有显著的影响作用。但林分水平空间结构与林分垂直空间结构与林下草本物种多样性指数均呈正相关,而林木竞争指数却与林下草本物种多样性指数均呈负相关,且三者对同一物种多样性指标的影响程度也存在差异,林分水平空间结构更好地解释了林下草本物种多样性指数和均匀度指数的变异；林分垂直空间结构更好地解释了林下草本丰富度和物种均匀度指数的变异,而林木竞争指数却更好地解释了林下草本物种丰富度和物种多样性指数的变异。从影响系数看,林分水平空间结构的影响作用最大,垂直空间结构次之,林木竞争态势的影响作用最小。因此,欲维持或改善林下草本物种多样性,应采取调整林分水平空间结构为主,垂直空间结构调整为辅,并适当降低林木竞争程度的综合经营措施。