基于模糊综合评价法的公路工程施工质量评估模型应用

贾荷柱

（山西诚达公路勘察设计有限公司，山西 太原 030006）

改革开放以来，经过几十年的快速发展，我国公路里程已经跃居世界第一。当前，我国仍然保持着在交通基础设施建设领域的高水平投入。公路作为支撑国民经济发展的重要基础设施和现代化标志，其建设和运营质量不仅反映着一个国家的综合国力，也深刻影响着社会生活的方方面面，确保公路工程建设质量对于提高社会经济发展水平和人民群众生活质量具有重要意义。

公路工程是一个复杂的系统工程，建设周期长、影响因素多，因此，借助科学有效的数学方法进行施工质量管理就显得尤为迫切和必要。基于此，本文在前人研究的基础上，建立了公路工程施工质量评价指标体系，提出了基于模糊综合评价法的公路工程施工质量评估模型，以期能够为公路工程建设质量管理提供一定的借鉴和指导。

1 质量评价指标体系的建立

能否建立科学的质量评价指标体系直接关系到评价结果的准确性，因此，质量评价指标的选择必须遵循科学的指标选取原则，即客观性、全面性、相关性、实用性、层次性原则[1]。

基于以上原则，并结合以往学者研究[2]，本文建立了公路工程施工质量评价指标体系，见表1。

表1 公路工程施工质量评价指标体系

2 模糊综合评价模型的构建

模糊综合评价法是一种系统性较强的综合评价方法，通过模糊数学理论将定性问题转变为定量问题，十分适用于处理模糊、难量化、非定型问题。本文基于模糊综合评价法构建公路工程施工质量评价模型的基本步骤如下。

2.1 基于改进AHP法计算指标权重

科学计算各级指标权重是确保公路工程施工质量评价结果准确的关键。本文采用改进AHP法计算指标权重。

AHP法是一种将定量分析与定性分析结合起来的综合评价方法，广泛应用于各种评价领域。它将复杂的问题进行拆分，并对各项指标之间的重要程度做出比较，从而生成判断矩阵，再通过该矩阵计算得到指标权重[3]。然而，传统的AHP法受到主观因素干扰较大，而且需要进行一致性检验并经过多次调试，因此就显得比较复杂低效。

鉴于此，本文引入改进AHP法，以期有效避免主观因素干扰，简化计算流程，提高评价效率[4]。具体计算步骤如下。

2.1.1 计算比较矩阵

引入九级标度法构造判断矩阵，比较标度定义见表2。

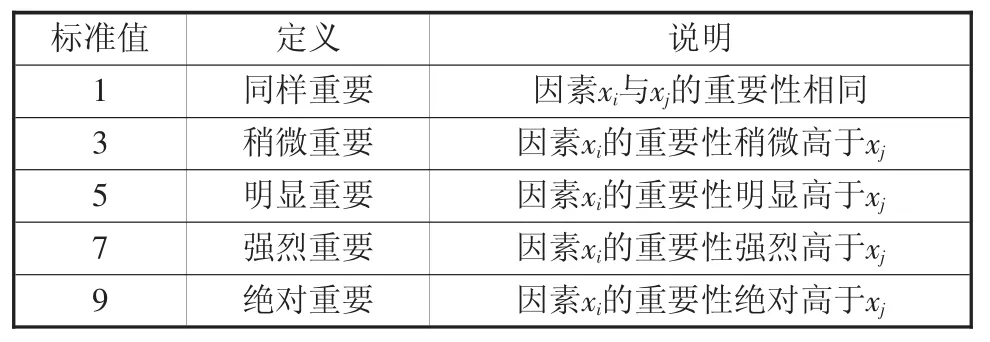
表2 比较标度

基于九级标度法，综合专家意见，构造比较矩阵A，即

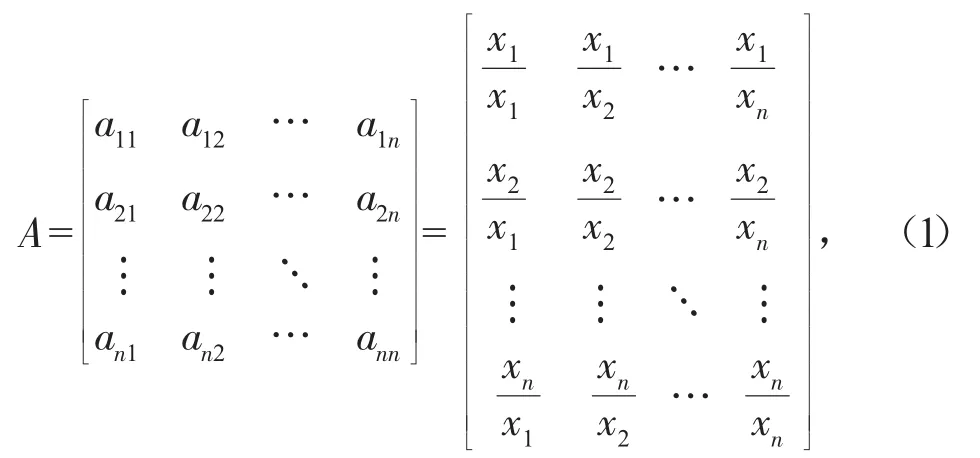
式中：aij(i,j∈n)代表第i个指标与第j个指标基于比较标度的比较结果。

2.1.2 计算排序指数

求出指标层中第i个评价指标相对于准则层中某个元素重要性的比较结果，并将比较结果求和得到排序指数如式（2）。

2.1.3 构造判断矩阵

由排序指数ri构造判断矩阵Bij，该矩阵中各元素bij可由式（3）得到。

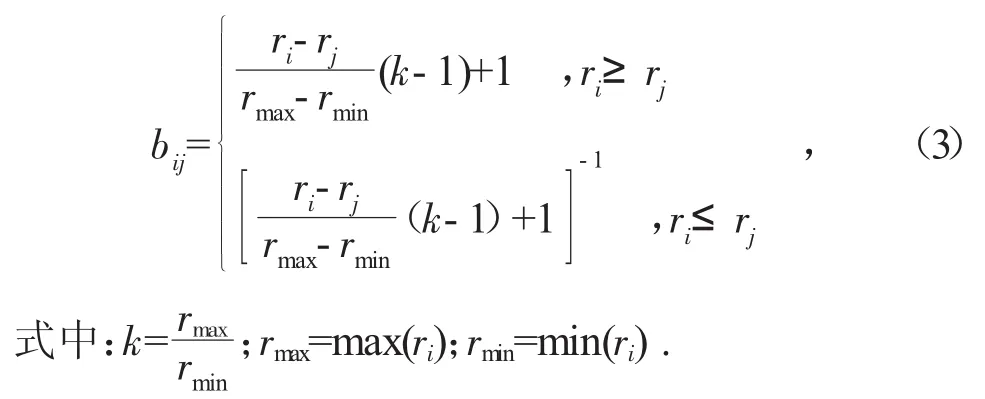
2.1.4 计算拟优一致矩阵

设拟优一致矩阵为B'ij,则其矩阵中的各元素b'ij由式（4）求得。

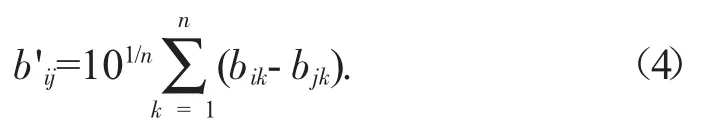
2.1.5 计算指标权重

对拟优一致矩阵B'ij做归一化处理得到矩阵Tij，设矩阵中元素为tij，则可按照式（5）计算指标权重。

最终得到指标权重向量：

2.2 建立评语集

所谓的评语集是指评价对象所涉及到的各因素的评价等级，即评语集的元素组成是评价等级。本文综合前人的研究成果[5-6]，结合项目具体情况，拟定公路工程施工质量评价等级，见表3。

表3 公路工程施工质量评价准则

给定评价等级后，邀请该研究领域的n个专家对m个指标进行打分，由此获得原始数据矩阵。

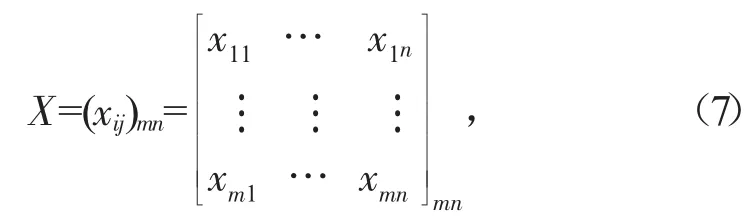
式中：xij表示第j位专家对第i个指标的打分。

2.3 指标单因素模糊评价

首先需要对单个评价指标进行模糊评价，以确定单个评价指标对质量等级的隶属程度。隶属度一般通过建立常用的隶属函数,并代入实际数据计算得到。基于指标数据的分布特征，参考以往学者的使用经验，建立了“梯形分布”隶属度函数[5]，该函数如式（8）：

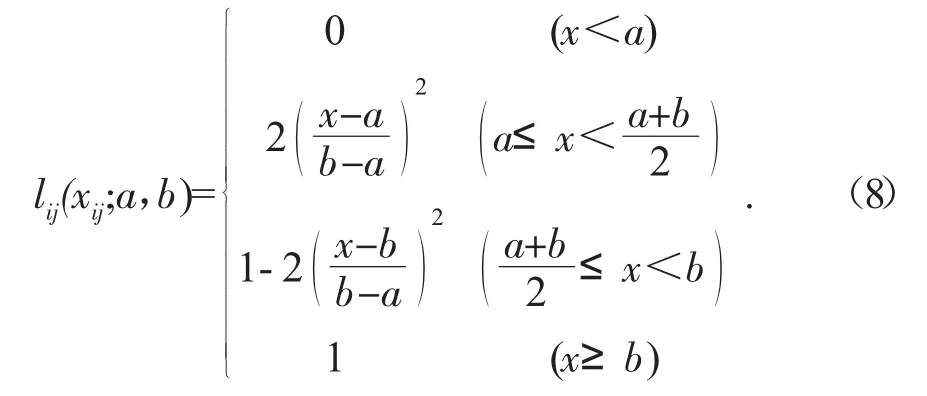
通过隶属度函数，可以得到评价指标对评价集中的评价等级的隶属度，之后得到单个评价指标的隶属度向量：

在得到m个评价指标的隶属度向量之后，可以得到一个隶属度矩阵：

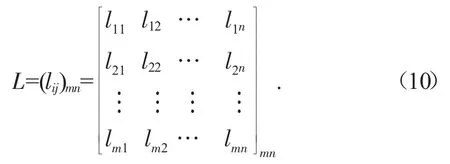
2.4 模糊综合评价

在得到隶属度矩阵L之后，就可以对各评价指标的评价结果进行综合，最终得到该评价对象的综合评价结果，即：

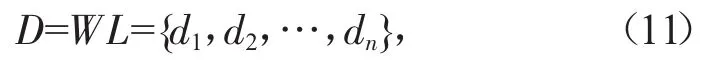
式中：D表示模糊综合评价集；dj代表该评价对象整体对评价等级j的隶属程度。一般来说，可采用最大隶属度来确定最终评价结果，即隶属度向量D中值最大的元素所对应的评语集中的评价等级。

3 实例应用

本文依托山西省国道241、省道岚马线汾河水库段改线工程进行模型应用。该项目位于岚县、娄烦县和古交市境内，连接岚县和娄烦县，是太原市、吕梁地区公路网中的主干线，是娄烦县与山西省西北部各县联系和交流的重要通道。该项目的建成能够优化区域路网结构、拓展地区发展空间、促进地区社会经济发展和改善民生，为土地和旅游资源开发起到巨大的推动作用。该线起点位于岚县梁家庄，终点位于古交市梭峪乡梭峪村南侧，路线全长16.288 km，设计速度60 km/h。

首先基于改进AHP法，结合专家经验，构造比较矩阵，首先构造目标层-准则层比较矩阵。

同理，可构造准则层-指标层比较矩阵，如

然后代入式（2）～式（6）可计算得到该项目施工质量评价指标权重，见表4。

表4 汾河水库段改线工程施工质量评价指标权重

然后邀请5位公路工程施工质量研究领域的专家对该项目工程施工质量评价指标体系中的19个三级指标进行打分，见表5，由此得到原始评分数据矩阵。

表5 专家评分表

根据式（8）～式（10）可计算得到各指标对不同施工质量等级的隶属度，见表6。

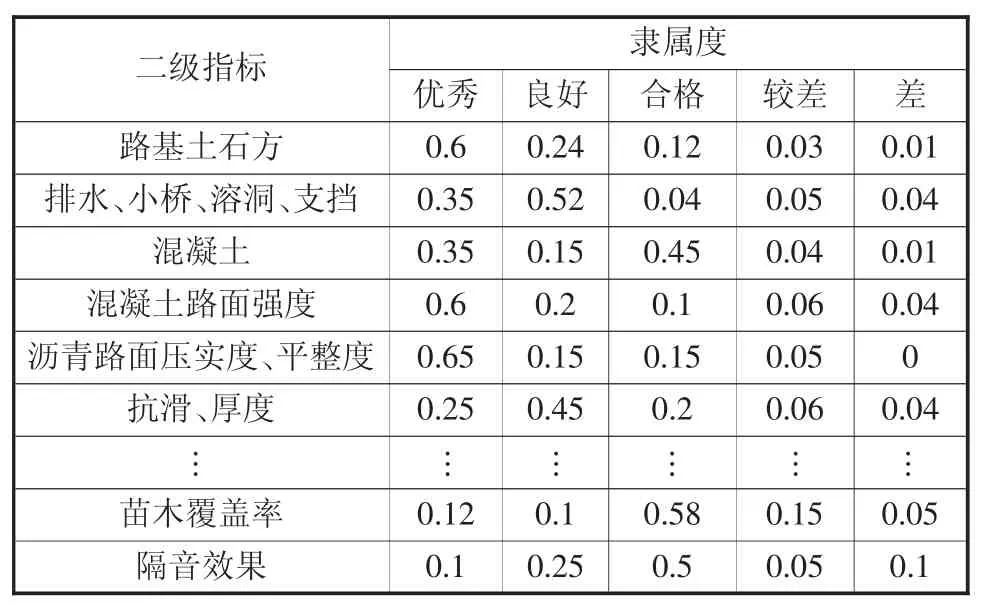
表6 汾河水库段改线工程施工质量评价指标隶属度

最后根据式（11）可计算得到评价对象总的隶属度：

D=WL={0.1367,0.4631,0.2021,0.1286,0.0695}.

根据最大隶属度原则，可得隶属度中的最大值为0.463 1，对应的施工质量等级为良好，即山西省国道241、省道岚马线汾河水库段改线工程施工质量为良好。同时，根据最大隶属度原则对上述二级指标的质量等级进行界定，可以看出应该着重提高环保工程质量，如提高苗木覆盖率、适当优化隔音等相关工程建设，以进一步提高公路工程施工质量。