基于EMD自适应阈值的铡草机振动信号去噪

王晓蓉 王海超 王春光*

(1.内蒙古农业大学 机电工程学院，呼和浩特 010018；2.内蒙古农业大学 能源与交通工程学院，呼和浩特 010018)

铡草机是我国使用最早、应用较广泛的饲草料加工机械[1-2]，研究其振动信号能为机具优化设计，提高机具生产率与降低功耗提供理论依据。采集振动信号时，由于秸秆加载、传感器及传感器线固定等问题，机具的振动信号必然会受到噪声干扰，从而会降低后续分析的准确性[3-4]。铡草机振动信号是一种非线性、非平稳信号，传统去噪方法受到限制，因此，铡草机振动信号去噪算法的研究，对指导铡草机结构设计与改善生产环境具有一定意义。

目前，小波阈值去噪是一种适用于非平稳信号去噪的算法[5-6]，并以此为基础，发展了许多关于改进阈值与阈值函数的新算法[7-8]，其中小波自适应阈值去噪算法被广泛应用[9-10]，但其仍存在小波基函数与分解层数选择困难的问题。已有研究提出了EMD(Empirical mode decomposition)分解[11]，该方法对非平稳信号具有良好的适应性与多分辨率特性，可实时、高效分解信号，故被应用于非线性、非平稳信号去噪[12-13]，但其直接将高频分量滤除，会导致信号失真。在此基础上，将小波阈值去噪与EMD分解结合[14-16]，克服了EMD去噪算法粗疏的问题，但该算法延续了小波阈值去噪的阈值选取方法，不能根据信号分解的不同而自适应改变，无法达到精确去噪。

基于上述分析，本研究在分析总结已有算法的基础上，将EMD与基于SURE(Stein’s unbiased risk estimate)的小波自适应阈值去噪相融合，拟采用EMD方法分解信号，利用自相关函数特性判断含噪分量，基于二阶可导阈值函数与SURE自适应阈值理论，实现铡草机振动信号自适应阈值去噪。

1 信号去噪

1.1 EMD阈值去噪

x(i)=s(i)+e(i)i=1,2,…,N

(1)

EMD阈值去噪算法流程见图1，具体步骤如下。

1)含噪信号x(i)经EMD分解的结果为：

(2)

式中：imf为本征模态函数，且频率由高到低排列；r(i)为残余分量；j为本征模态函数的个数。阶数低的imf对应信号高频成分，一般认为噪声主要集中在高频部分，阶数高的imf对应信号低频成分，受噪声影响较小。

图1 EMD阈值去噪流程Fig.1 Denoising flow chart of EMD threshold

2)对各阶imf求自相关函数。由于自相关函数反映了信号在不同时刻的相关程度，故含噪分量的自相关函数在零点处取得最大值，而其他点处迅速衰减至零[17]，利用此特点可以确定分界值k，即imf1～imfk分量含有噪声，imfk+1～imfn分量为不含噪声。

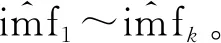
(3)

1.2 基于SURE的小波自适应阈值

选取合适的阈值与阈值函数是算法的核心内容，本研究将基于SURE小波自适应阈值与EMD阈值去噪思想相结合，依据最小均方算法，确定最佳分层阈值。根据含噪信号数学模型(式(1))，在空间域内，设观测值的函数为[18]：

(4)

g(X)属于从RN到RN的映射，若g(X)可微，则g(X)的SURE为：

(5)

其中：

本研究中，将含噪imf分量当做小波系数，观测信号可改写为：

(6)

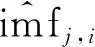
(7)

其中：

(8)

由于工程应用中真实信号s(i)无法获取，故采用SURE无偏估计，即SURE代替MSE[19]。

最小均方算法LMS(Least mean squares)是神经网络算法(Neural Networks Algorithm)中最实用的方法之一。使用LMS算法，利用最速下降算法，沿着SURE最速下降方向(负梯度方向)调整每个含噪分量imf的阈值，即下一时刻的分层阈值λj(m+1)等于现时刻的分层阈值λj(m)加负均方误差函数对λj(m)的梯度值。LMS算法迭代公式为：

(9)

式中：

式中μ为迭代步长。将式(7)代入式(9)，得：

(10)

(11)

式中：β为正整数。阈值函数式(11)的一阶导数和二阶导数为：

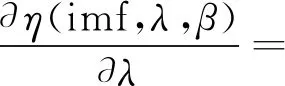
(12)

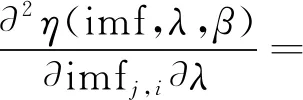
(13)

1.3 基于EMD自适应阈值算法

本研究算法结合了EMD阈值去噪算法与基于SURE自适应小波阈值去噪算法。本研究算法流程见图2，实现过程如下：

1)EMD分解。采用式(2)对含噪信号x(i)进行EMD分解，并对所得n个imf求自相关函数，确定前k个imf为含噪分量。

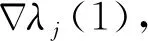
(14)

式中：σj=MAD(|imfj,i|)/0.674 5，MAD(*)为中值函数。

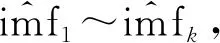
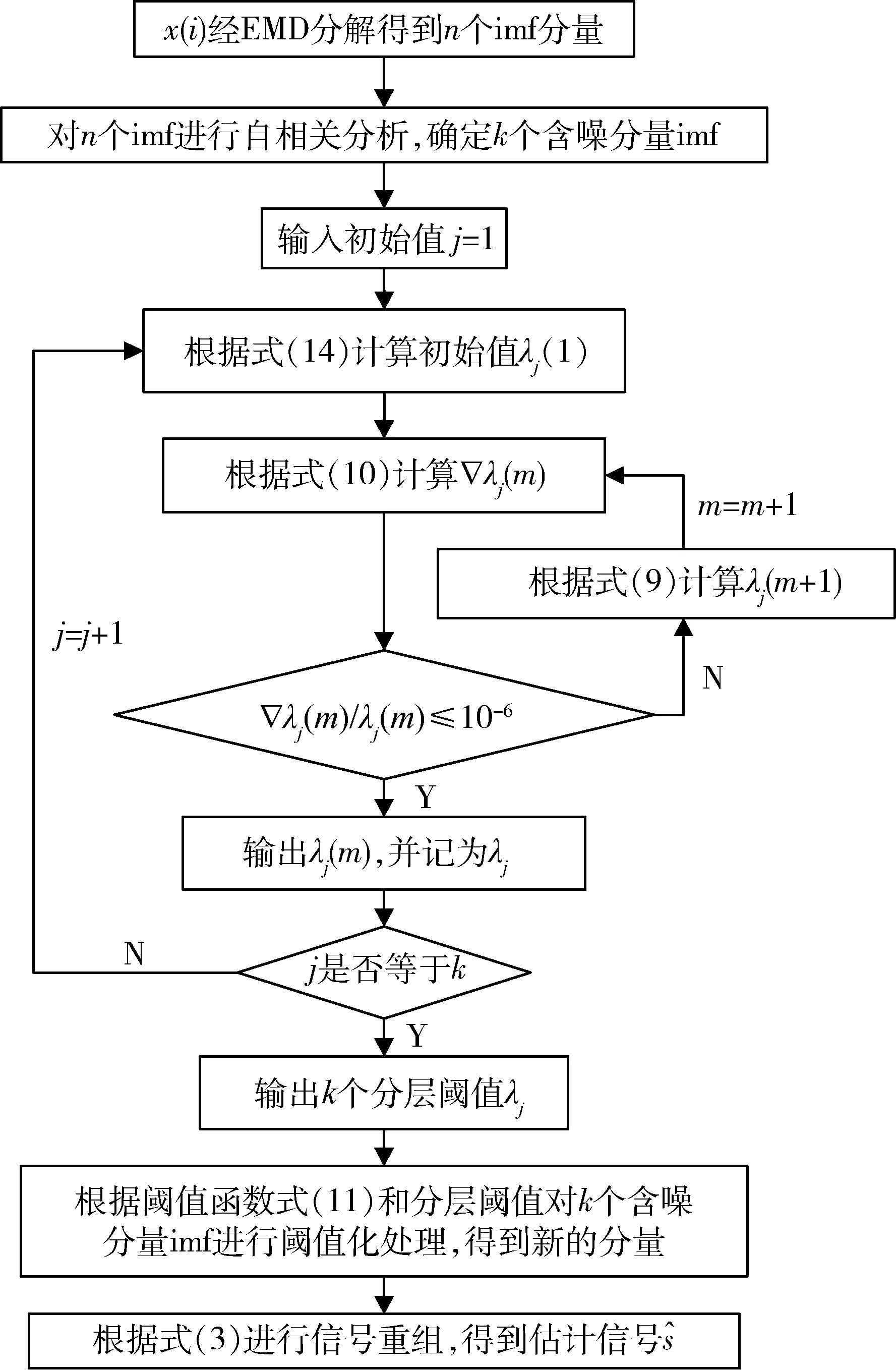
图2 本研究算法去噪流程Fig.2 Denoising flow chart of proposed algorithm

2 仿真分析

2.1 评价标准

本研究采用信噪比SNR(Signal to-noise ratio)定量评价算法去噪效果。去噪后SNR值越大，表明去噪后信号与原信号接近程度越大，证明该算法去噪性能越好。SNR计算公式为：

(15)

2.2 试验方法

从MATLAB自带基准信号中选取具有代表性的4种基准信号：block、bumps、heavy sine与doppler，截取信号长度为2 048点，与高斯白噪声叠加，得到SNR为5的含噪信号。采用小波阈值去噪法、EMD低通去噪法、EMD阈值去噪法与基于SURE的EMD自适应阈值去噪法进行对比试验，并使用SNR定量评价去噪后信号质量。

小波阈值去噪法中，选用sym5小波，分解层次为6层，软阈值函数，阈值采用式(14)确定，其中，方差估计用小波系数计算。EMD阈值去噪法采用软阈值函数，阈值根据式(14)确定。

2.3 结果分析

由图3可以看出，虽然4种算法均有可观的去噪效果，但与本研究方法相比，后者去噪后曲线比较光滑，尤其在信号长度为1 000～1 500点。由表1可见，对于4种不同的信号，4种方法去噪效果优劣排序为：EMD自适应阈值>EMD阈值>小波去噪>EMD低通。EMD低通去噪后SNR最低，因为其忽略了高频中的有效成分。而小波阈值去噪法与EMD阈值去噪法唯一不同的是分解方式，表明小波去噪法受限于小波基与分解层数的选择。EMD自适应阈值法的去噪结果最好，说明基于SURE自适应阈值的选择比固定阈值更为准确。综上所述，本研究结合了EMD分解与小波自适应阈值的优势，故与其他3种方法相比，去噪效果最优。

图3 不同算法对heavy sine的去噪结果Fig.3 Denoising results of heavy sine by different algorithms

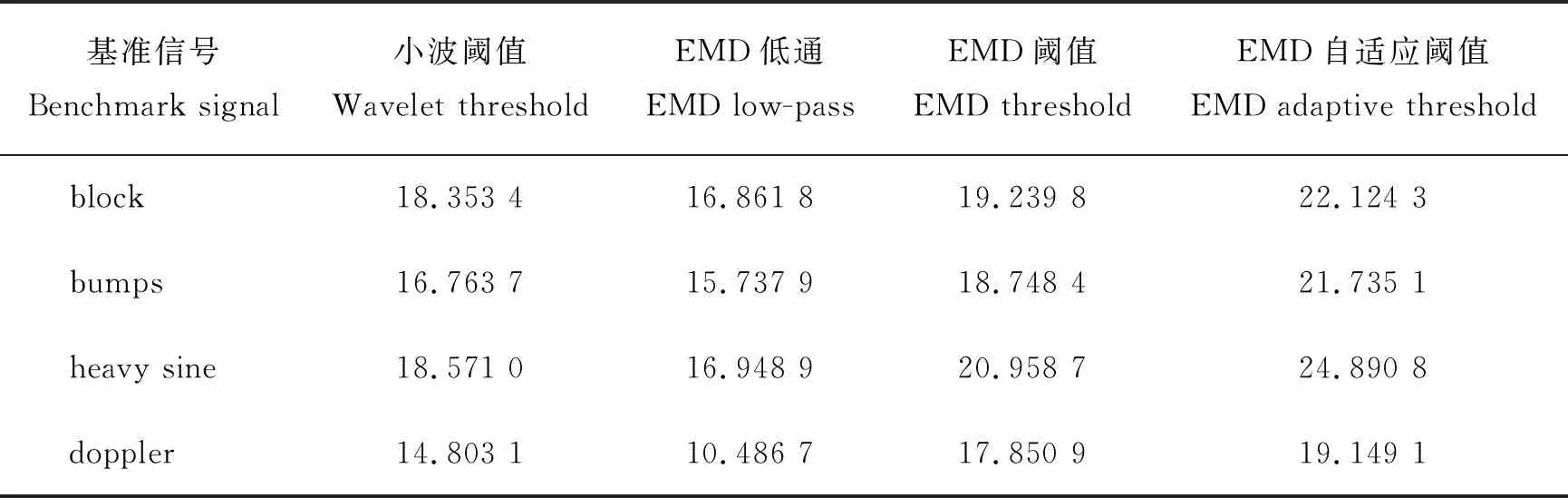
表1 不同算法对模拟信号去噪后的信噪比Table 1 SNR of analog signals after denoising by different algorithms

3 铡草机振动信号试验与结果分析

3.1 测试方案

本研究主要针对家庭使用铡草机为研究对象，由于9Z-4C型青贮铡草机使用较多，故选择为样机。该样机额定转速为800 r/min。铡草机工作时，铡切装置的动刀刀盘高速旋转，及物料、气流等综合作用，使铡草机产生振动。进料口、喂入辊、变速箱、刀盘、出料口是试验样机的主要旋转部件与工作部件，故选择这5个部件的外壳中心为测试测点。为了方便信号分析，规定样机正转时输送链运动方向为X方向，根据右手规则，水平面上垂直于X方向为Y方向，垂直于水平面为Z方向，三向加速度传感器的3个通道对应样机规定方向安装。

采用MI7106动态信号分析仪与3263A2三向加速度传感器组成测试系统，实现整机空载与负载2种工况下多点振动测试，得到5个测点时域波形。测试系统见图4，其中，分析仪的采样频率为1 500 Hz，采样点数为4 096点，采样时间1 min；加速度传感器的量程为50g，频响为1.5～1 000 Hz，灵敏度为100 mV/g。

图4 铡草机振动信号采集和测试系统Fig.4 Vibration signal acquisition and testing system of chaff cutters

经理论计算，铡草机振动信号频率集中在 200 Hz 以下的低频区域，由于机器运行与物料加载，加速度幅值大，并衰减迅速；噪声信号则呈高频特性，分散于整个信号，加速度幅值较小，波形均匀连续、无突变现象。

3.2 试验方法及结果分析

为对比4种算法去噪性能，任取一组铡草机振动信号，分别用4种算法对其进行去噪，并使用去噪后振动信号自功率谱图衡量算法优劣。原始振动信号的自功率谱与小波阈值去噪、EMD低通去噪、EMD阈值去噪后铡草机振动信号的自功率谱见图5。可见：1)原始振动信号频率分布于0～1 000 Hz，高频对应的幅值部分位于200 Hz以上，低频部分对应的幅值基本位于200 Hz以内。2)小波阈值去噪后，大于200 Hz的部分，频率幅值大幅度减小，但依然存在。说明小波阈值算法去噪能力有限，对于高频信号去除不彻底。3)EMD低通去噪法与EMD阈值去噪法去噪后，虽然克服了小波阈值算法缺点，大于200 Hz的高频幅值趋近于0，但与原始信号自功率谱图相比，这2种算法在200 Hz以内能量明显降低，这是由于EMD低通算法直接去除了高频imf分量，EMD阈值算法的阈值选取不合适，导致部分真实信号连同噪声被一起去除，造成信号失真。4)本研究方法去噪后，不仅消除了大于 200 Hz 的高频信号，还对高频imf分量进行了自适应阈值去噪，有效提取了有用信息，避免了信号失真。相比其他3种算法，本研究算法对于铡草机振动信号去噪效果更完全。

图5 不同算法去噪后铡草机振动信号的自功率谱Fig.5 Self-power spectrum of vibration signals of chaff cutters after denoising by different algorithms

4 结 论

在采集铡草机振动信号过程中，信号不可避免会受到噪声污染，为了解决振动信号含噪问题，本研究提出了一种基于二阶可导阈值函数的方法，结合基于SURE的自适应阈值，实现了EMD去噪最优阈值的自适应选择。通过对模拟信号与铡草机振动信号去噪试验分析，得到以下结论：

1)本研究结合EMD与小波自适应阈值去噪的优点，弥补了小波去噪中选择小波基与分解层数的不足，解决了EMD去噪粗略的问题。

2)对模拟信号block、bumps、doppler与heavy sine进行去噪，对比分析小波阈值去噪法、EMD低通去噪法、EMD阈值去噪法与本研究算法的去噪效果。通过定性与信噪比SNR定量分析各算法去噪结果，本研究算法比其他3种算法能够更有效地去除噪声，去噪后信号的SNR最高，并减小了对原始信号畸变。

3)对实测铡草机振动信号进行去噪，对比原始测信号自功率谱图与4种方法去噪后的自功率谱图，本研究在消除高频噪声信号的同时，还能保留有用低频信号幅值，避免了其他方法产生失真的现象。

综上所述，EMD自适应阈值去噪算法具有通用性，在铡草机振动信号降噪应用中具备良好去噪效果。