基于采样值排序的音频可逆隐写算法
2021-01-15王让定严迪群张雪垣
余 恒,王让定,严迪群,张雪垣
(宁波大学信息科学与工程学院,浙江宁波 315211)
0 概述
信息隐藏是指在人的感官无法察觉的情况下,将秘密信息嵌入到各种数字媒体中,如图像、音频和视频等。在嵌密结束后,传统信息隐藏载体会产生不可逆的失真,这被称为不可逆信息隐藏,在一些特殊场合,这种失真是不被允许的[1]。为了解决该问题,研究人员提出了可逆信息隐藏技术[2],其特点是在秘密信息被提取完毕后,原始载体能够被完整恢复并且没有任何失真,这种特性使得该技术在一些如图像处理、对抗样本等[3]重要领域有着广阔的应用前景。
2003 年,TIAN等人[4]提出一种基于差值扩展(Difference Expansion,DE)的可逆信息隐藏方法,其首先对连续的2 个像素值做差,然后将差值转化成二进制形式,最后将密信比特追加到二进制差值的最低位上。该方法操作简单,但是相邻像素之间的差值在扩展之后失真较大。THODI 等人[5]在DE 的基础上,提出利用预测误差来替代相邻像素的差值进行扩展嵌密的方法,实验结果表明,预测误差扩展(Prediction Error Expansion,PEE)相较DE 具有更低的失真,因此,PEE 引起了研究人员的广泛关注[6-7]。
上述方法的本质都是借助差值、预测误差等进行扩展嵌密,对载体的修改较大,在解决失真问题上的效果较直方图移位(Histograms Shift,HS)方法差。TSAI[8]将预测误差与HS 相结合,在增加一部分嵌密容量的前提下有效降低了失真。OU 等人[9]又在TSAI 的基础上利用多个直方图修改(Multiple Histograms Modification,MHM)来进行嵌密,弥补了TSAI 在嵌密容量上的不足。2013 年,LI 等人[10]提出一种像素值排序(Pixel Value Ordering,PVO)的可逆隐写框架,其将一副图像分成若干个固定大小的像素块,然后对像素块中的像素值进行排序,通过第二大(小)值来预测最大(小)值,最后将密信嵌入到预测误差值为“1”或“-1”的像素值中。由于该框架只对载体进行了少量修改,因此隐写后的载体具有高保真的特点。PENG 等人[11]在PVO 的基础上提出改进的像素值排序(IPVO),其增加预测误差“0”作为嵌密条件,有效提高了嵌密容量。WENG 等人[12]对像素块内的预测机制进行研究,增加了像素块内生成的预测误差个数,提高了块内像素的利用率。
目前,关于可逆隐写的研究工作大多集中在图像领域[13-15],而较少关注以音频为载体的可逆隐写算法。严迪群等人[16]将DE 框架应用在音频载体上,证实了DE 框架的通用性。WANG[17]结合音频的特点,提出一种基于改进的预测误差扩展和直方图移位的新型可逆音频水印方案,与严迪群等人方法相比,其进一步提高了嵌密容量与信噪比。XIANG[18]将音频时域采样值按照位置的奇、偶分成2 个集合,提出一种复杂的非因果预测算法来计算预测误差,然后将密信以扩展的方式嵌入到预测误差中,该方法的预测性能是目前较优的。文献[19]在XIANG 算法的基础上对容量控制进行优化,在高嵌入率的情况下其性能得到一定提升。
当前关于音频可逆隐写的研究大都围绕PEE[20-21]展开,限制这类算法性能提升的主要因素包括预测精度和嵌密机制2 个。尽管XIANG 将预测精度提升到了一个新高度,但是其仍然利用预测误差的二进制扩展进行嵌密,这种方法对载体的修改幅度较大,难以获得高保真的嵌密效果。
本文提出一种针对音频载体的PVO 可逆隐写算法。将音频时域序列分成若干个大小相同的采样块,利用音频时域相关的特点对每个采样块的复杂度进行评估,根据复杂度来确定采样块是否能够进行嵌密。此外,由于采样块的大小直接影响嵌密效率,本文进一步利用采样块的复杂度来确定最优预测采样值,以此提高采样块的嵌密效率。
1 基于IPVO 的可逆隐写算法
PENG等人[11]提出的基于IPVO 的可逆隐写算法,将载体图像划分为若干个大小为n的非重叠像素块,并将这些像素块内的像素值按照升序进行排列,得到一个有序集合{xσ(1),xσ(2),…,xσ(n)}。其中,xσ(1)≤xσ(2)≤…≤xσ(n),xσ(i)表示有序集合中的第i个像素值,σ(i)表示xσ(i)在原始像素块中的位置。
将像素值xσ(2)与xσ(n-1)作为预测像素值,分别用来预测xσ(1)与xσ(n)的大小。对于xσ(1),通过式(1)得到预测误差PEmin:

然后利用式(3)将密信比特b∈{0,1}嵌入到预测误差中得到
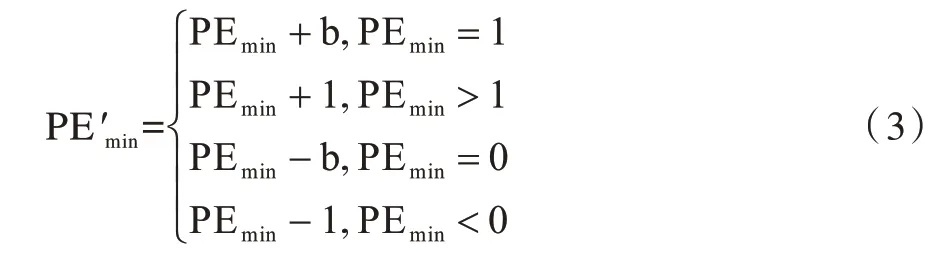
再利用式(4)得到xσ(1)的预测值
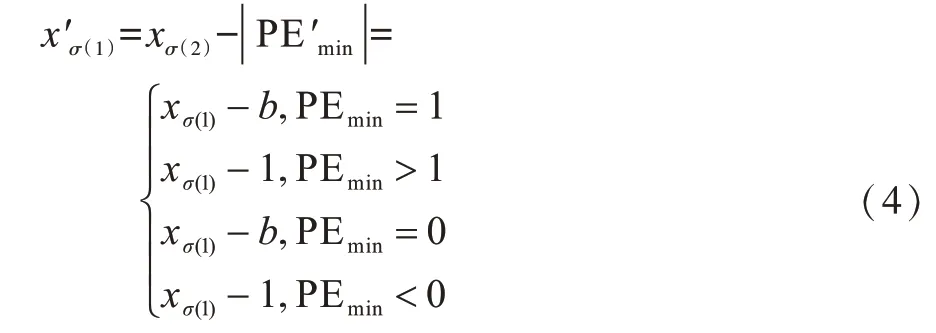
最后得到含密像素块Y=(y1,y2,…,yn),其中,,对于任意i≠σ(1),yi=xi。

其中,s和t的计算方法与嵌密时一致。然后根据得到的对xσ(1)进行恢复:
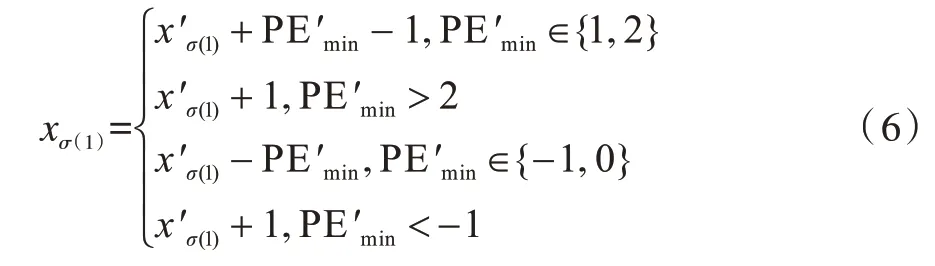
同时提取出嵌入的密信比特b:
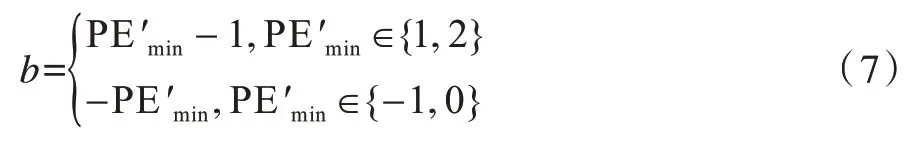
与最小值xσ(1)的嵌密操作相似,通过式(8)将xσ(n)修改为从而对最大值xσ(n)进行嵌密:
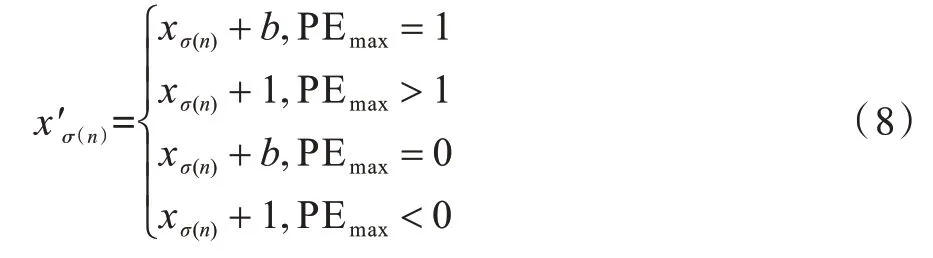
其中:
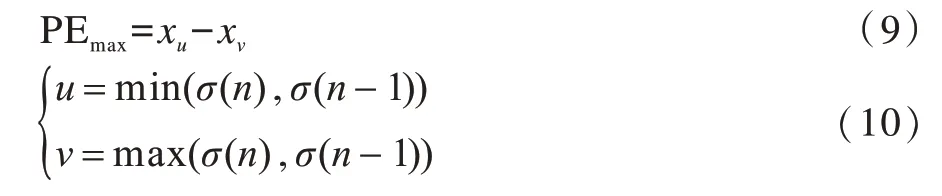

其中,u和v的计算方式与嵌密时一致。然后根据得到的进行恢复:
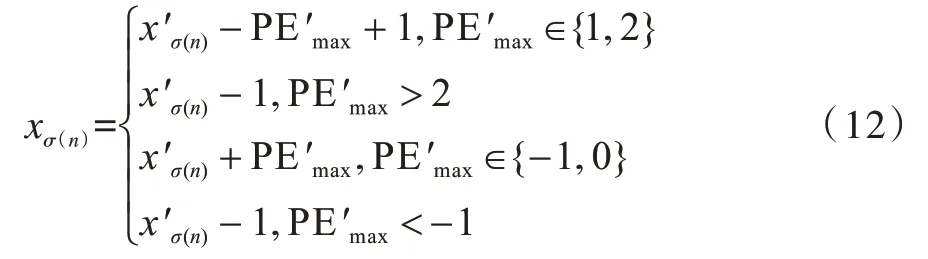
同时提取出嵌入的密信比特b:
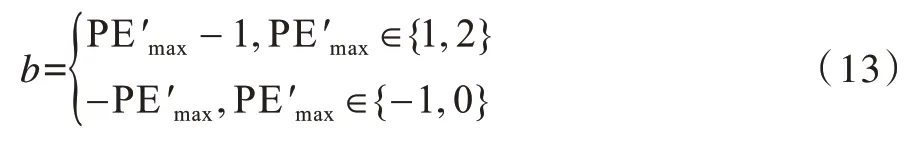
PENG 等人根据排序后的相邻像素具有高度相关的特性,利用第二小(大)的像素去预测最小(大)的像素。将密信比特嵌入到符合条件的预测误差中,对于不符合要求的预测误差,通过加1 或者减1来进行移位,以此保证解密的正确性。该方法对载体的修改较少,符合高保真的要求。然而,当分块大小n增大时,其仅预测最小(大)值可能会对其他像素值造成浪费。本文对此进行改进,并将该方法应用于音频载体上。
2 音频可逆隐写算法
本文引入采样块复杂度的概念,对采样块复杂度等级进行评估,得出最优预测采样值,利用最优预测采样值实现采样块的高效利用。
2.1 采样块复杂度
一些无损格式的音频采样值范围通常较大,在对音频载体进行分块后,如果不对采样块加以区分,会造成不必要的失真。因此,本文引入采样块复杂度Δ来衡量一个采样块内部采样值的变化幅度。首先利用事先设定的复杂度阈值Cz将采样块分成复杂块(Δ>Cz)与平滑块(Δ≤Cz),然后在进行嵌密操作时,对平滑块进行嵌密,对复杂块直接跳过。
实际上,音频的采样值是时域相关的,一个采样值的大小与其前后的采样值之间有着高度相关性。因此,本文通过与采样块相邻的前一个采样值xp与后一个采样值xq来计算该采样块复杂度。在给定密信长度的情况下,通过设定不同的阈值Cz可将密信自适应地嵌在不同的位置上。
2.2 最优预测采样值
对于一个大小为n的有序采样块X={xσ(1),xσ(2),…,xσ(n)},当n=3 时,用于预测的采样值被唯一确定,此时采样块的嵌密效率也最高,即由3 个采样值组成的采样块在理想状态下最多能嵌入两位密信。当n的值逐渐增大时,按照传统的方式选取用于预测的2 个采样值,位于这2 个采样值之间的采样值会被浪费,这样显然不合理。为此,本文设计一种确定最优预测采样值的机制,从而充分利用块内所有可能嵌密的采样值。
首先,将采样块的复杂度分为T个等级,1≤T≤m,其中,m=(n-1)/2」,·」表示向下取整。对于平滑块,满足条件的k即为该块的实际复杂度等级,最优预测采样值为xσ(k+1)与xσ(n-k),其中,k∈[1,T]。通过xσ(k+1)来预测比其小的所有采样值{xσ(1),xσ(2),…,xσ(k)},通过xσ(n-k)来预测比其大的所有采样值{xσ(n-k+1),xσ(n-k+2),…,xσ(n)}。当T确定时,{xσ(T+2),xσ(T+3),…,xσ(n-T-1)}在嵌密前后保持不变,将其记作xin。最后,将2.1 节的xp、xq与xin相结合以计算采样块的复杂度:
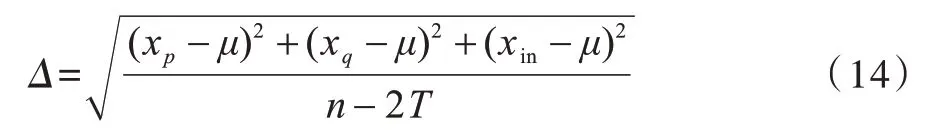
其中,μ表示xp、xq、xin的均值。
3 算法描述
3.1 嵌密算法
嵌密算法描述如下:
输入长度为N的音频载体S,长度为h的密信比特
输出一段含密音频S'
步骤1对音频载体S={x1,x2,…,xN}按照大小为n进行分块,得到采样块Si={xi+n·(i-1)+1,xi+n·(i-1)+2,…,xi+n·i},其中,xi+n·(i-1)、xi+n·i+1分别表示与子块Si相邻的前一个采样值、后一个采样值
步骤2依次遍历所有采样块,对当前子块的采样值按照升序排列,得到有序的采样块Xi={xσ(1),xσ(2),…,xσ(n)},其中,xσ(1)≤xσ(2)≤…≤xσ(n),σ(i)表示xσ(i)在原始采样块Si中的位置。
步骤3通过给定的复杂度等级T,得到子块内部用于计算复杂度的采样值{xσ(T+2),xσ(T+3),…,xσ(n-T-1)},将其与步骤1 得到的xi+n·(i-1)、xi+n·i+1相结合,通过式(14)来计算Si的复杂度Δ。
步骤4利用预先设定的复杂度阈值Cz对当前子块Si进行判断,如果Δ>Cz,说明当前子块Si属于复杂块,不做任何操作并将该采样块的采样值按照原始顺序放回S中,然后转到步骤2;如果Δ≤Cz,说明该块属于平滑块,进入步骤5。
步骤5由2.2 节得到最优预测采样值xσ(k+1)与xσ(n-k),利用式(1)、式(9)来预测{xσ(1),xσ(2),…,xσ(k)}与{xσ(n-k+1),xσ(n-k+2),…,xσ(n)},得到k个PEmin与k个PEmax,最后通过式(4)、式(8)将密信嵌入载体中。
步骤6判断密信是否嵌入完毕,如果还有密信未嵌入,则转到步骤2;如果密信嵌入完毕,进入步骤7。
步骤7嵌密结束,得到含密音频S'。
3.2 辅助信息
在嵌密过程中,由于采样值发生了改变,因此可能会产生溢出问题。为了解决该问题,本文建立一个位置映射图LM来标记可能产生溢出的采样块。16 bit 量化的音频采样值范围在[-32 768,32 767]之间,因此,如果当前块内有采样值等于-32 768 或者32 767,则令LM(i)=1;反之,LM(i)=0。在嵌密结束后,将得到的位置映射表LM进行无损压缩得到Ls。实际上,当分块大小确定后,LM的大小也被唯一确定。将压缩后的位置图Ls与分块大小n、复杂度阈值Cz、密信长度h、辅助信息结束标志EG依次连接组合成辅助信息L,将L 以LSB 替换的方式嵌入音频的开头部分。同时,为了保证可逆,把被L 替换的部分与密信一起嵌入载体中。辅助信息的各部分所占比特大小如表1 所示。

表1 辅助信息各部分所占比特大小Table 1 Bit size of each part of auxiliary information bit
3.3 密信提取与载体恢复
在接收到含密音频后,根据辅助信息结束标志EG提取出开头部分的辅助信息,依次得到位置映射表Ls、分块大小n、密信长度h,再将Ls解压缩得到原始的LM。解密过程具体如下:
输入含密音频S'
输出原始音频S,长度为h的密信
步骤1对含密音频载体S'按照大小为n进行分块,得到采样块,其中分别表示与子块相邻的前一个采样值、后一个采样值
步骤2依次遍历所有采样块,对当前块的采样值按照升序排列,得到有序的采样块表示在原始采样块中的位置。
步骤3通过给定的复杂度等级T,得到采样块内部用于计算复杂度的采样值,将其与步骤1 得到的相结合,通过式(14)来计算采样块的复杂度Δ'。由于用于计算复杂度的采样值在嵌密前后保持不变,因此Δ=Δ',从而保证了在解密时不会发生差错。
步骤4利用预先设定的复杂度阈值Cz对当前子块进行判断。如果Δ'>Cz,说明当前子块属于复杂块,不做任何操作并将该采样块的采样值按照原始顺序放回S'中,然后转到步骤2;如果Δ'≤Cz,说明该块属于平滑块,进入步骤5。
步骤5由2.2 节得到最优预测采样值与利用式(5)、式(11)来预测得到k个与k个最后通过式(7)、式(13)提取密信,利用式(6)、式(12)恢复载体。
步骤6判断密信是否提取完毕,如果提取完毕,则进入步骤7;否则,转到步骤2。
步骤7解密结束,得到长度为h的密信。
在解密后,根据辅助信息结束标志EG,将提取出的密信分成2 个部分,前一部分是原始载体头部的一段LSB 序列,将其进行替换得到完整的原始载体,后一部分即为密信。
4 实验结果与分析
4.1 实验设置
分块大小直接影响算法的性能,本文将分块大小n设置为{3,4,…,11},选取信噪比(SNR)值最高的分块大小用作最终嵌密。实验采用的载体为公开的EBU-SQAM 标准音频测试集[22],其包括70 段长度不一的音频序列。其中,(1、2)为噪音信号,(3~7)为人工信号,(8~43)为单一乐器音乐,(44~48)为纯人声音乐,(49~54)为人的语音,(55~60)为独奏乐,(61~64)为声乐与管弦乐,(65~68)为管弦乐,(69、70)为流行音乐。采样率为44.1 kHz,量化位数为16 bit。
为了简化操作,统一将载体设置为单声道。密信是随机生成的0 和1,共分为50 000 bit、100 000 bit 2 种长度。对比算法采用音频领域较具代表性的DE[16]和PEE[18]2 种算法,在Matlab R2018a 仿真软件上进行实验。
4.2 评价指标
SNR 与客观差异等级(ODG)常被用来评价隐写后的音频质量。SNR 的单位是分贝(dB),其值越高,代表隐写后音频的失真越小、质量越高。SNR 的计算公式为:
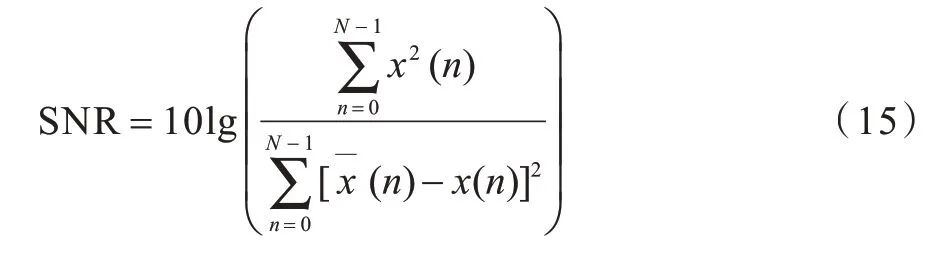
ODG 是一种音频质量客观评价指标,将参考信号和测试信号分别经过心理声学模型处理后,通过感知模型对参考信号与测试信号之间的声学特征差异进行综合评估,得到一个评价分数,即为ODG。ODG 的取值范围一般在[-4,0]之间,值越大表示音频的感知质量越高。
4.3 结果分析
隐写前后的音频波形在视觉上已无法分辨,原始音频波形如图1 所示,隐写后的波形(50 000 bit)如图2 所示,隐写前后音频波形的差值如图3 所示。
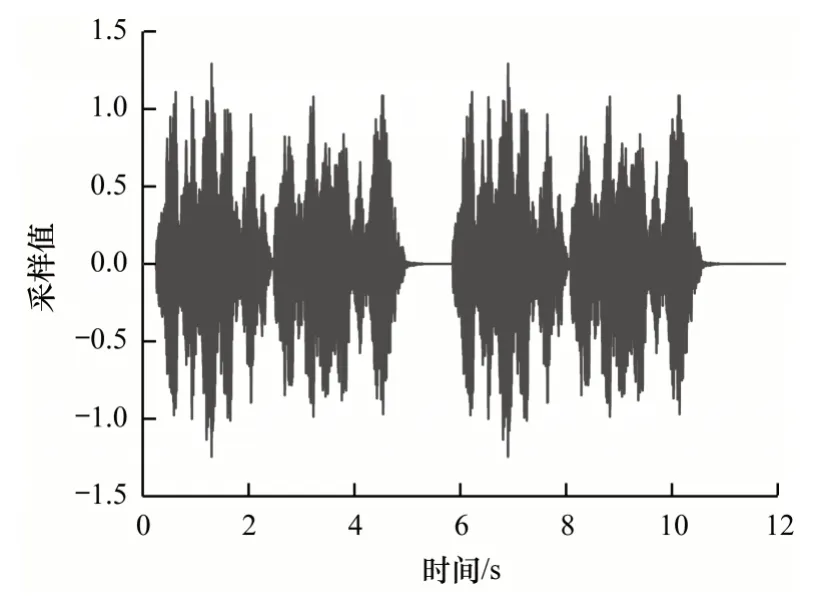
图1 原始音频波形Fig.1 Original audio waveform
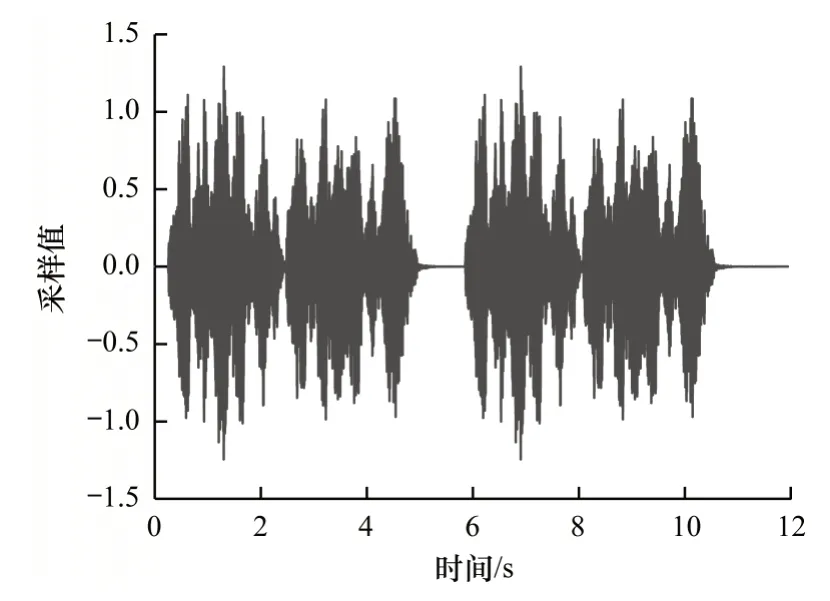
图2 隐写后的音频波形Fig.2 Audio waveform after steganography
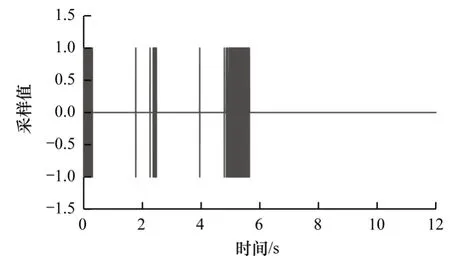
图3 隐写前后音频波形的差值Fig.3 The difference of audio waveform before and after steganography
将图1 与图2 进行对比可以看出,隐写前后音频在波形图上没有明显变化。从图3 可以看出,本文方法对采样值的修改幅度在[-1,1]之间,对载体的影响很小。为了进一步验证算法的优越性,将不同长度密信下的SNR 值与ODG 值进行对比,结果如表2~表5 所示,其中,最优结果加粗表示。
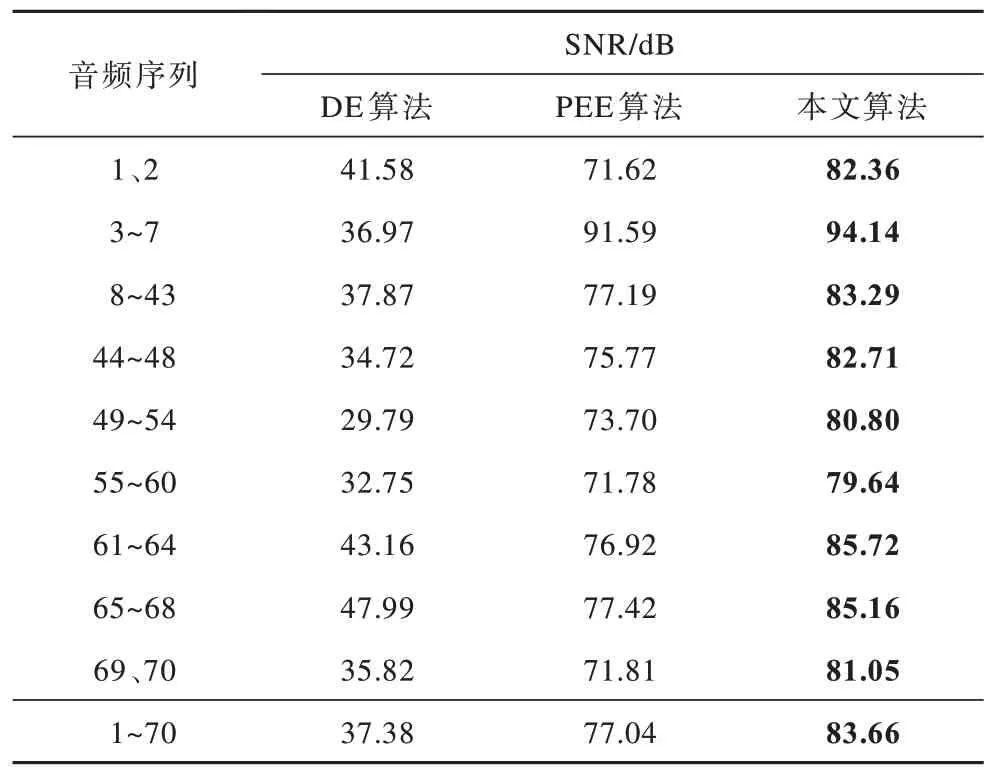
表2 密信长度为50 000 bit 时的平均SNR 值Table 2 The average SNR value when the secret message length is 50 000 bit
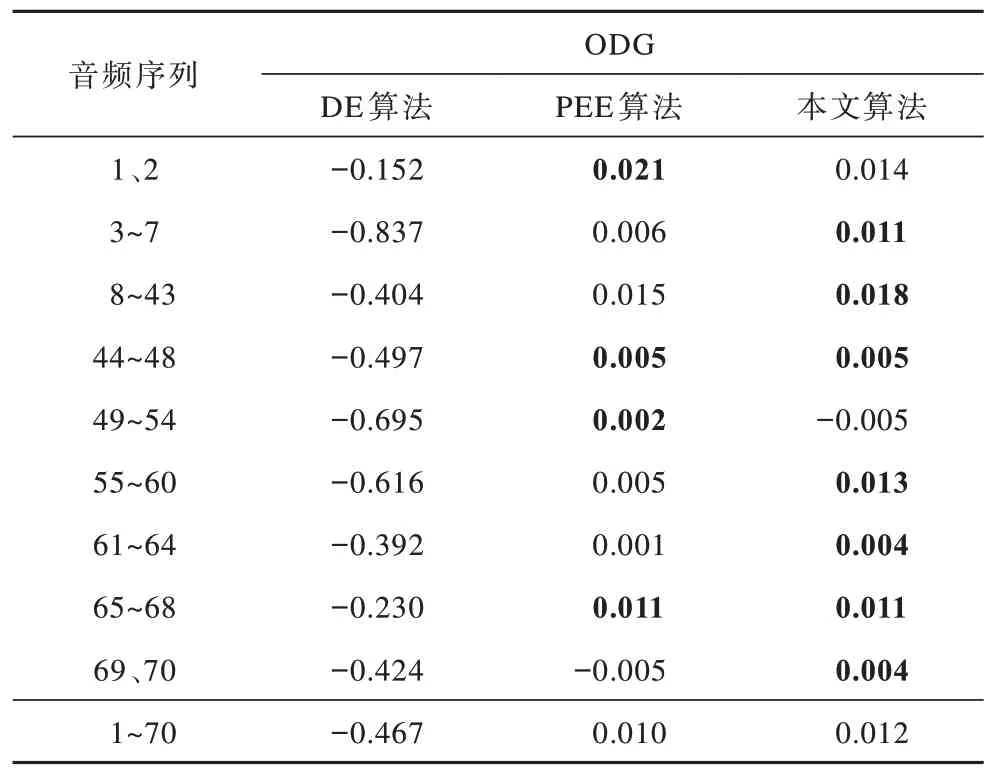
表3 密信长度为50 000 bit 时的平均ODG 值Table 3 The average ODG value when the secret message length is 50 000 bit
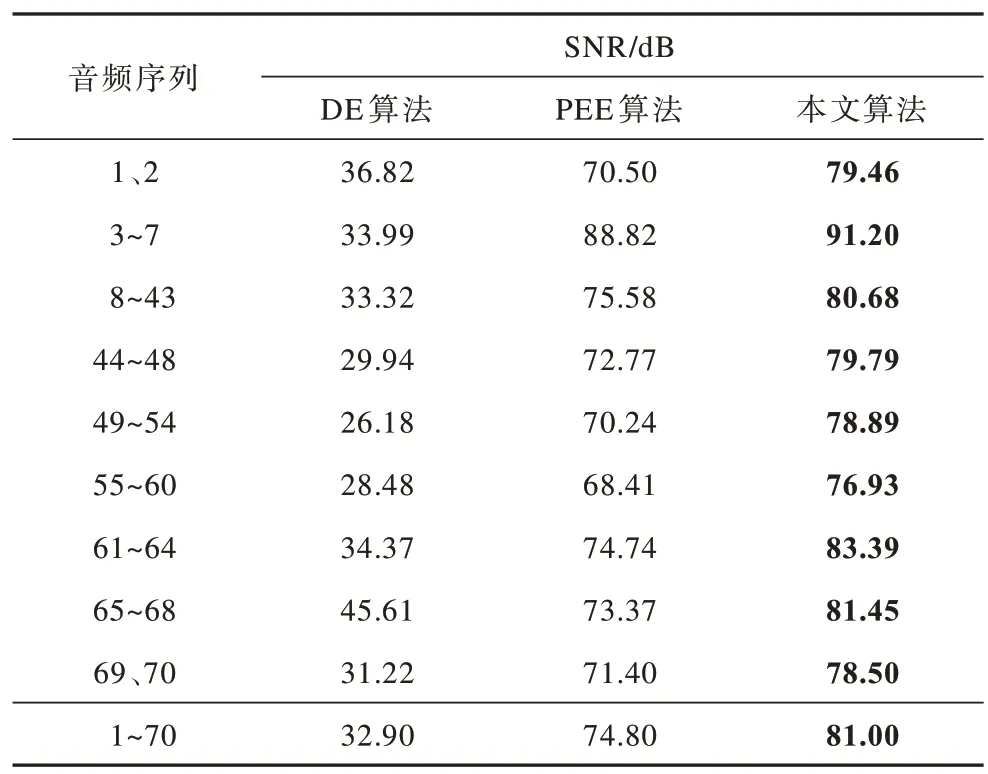
表4 密信长度为100 000 bit 时的平均SNR 值Table 4 The average SNR value when the secret message length is 100 000 bit

表5 密信长度为100 000 bit 时的平均ODG 值Table 5 The average ODG value when the secret message length is 100 000 bit
从表2、表4 可以看出,当密信长度为50 000 bit时,本文算法的平均SNR 值相比DE 算法、PEE 算法分别提高了46.28 dB、6.62 dB;当密信长度增加到100 000 bit 时,本文算法的平均SNR 值相比DE 算法、PEE 算法分别提高了48.10 dB、6.20 dB。对于9 种不同的音频,经过本文算法隐写后的SNR 值都有了明显提高,验证了本文算法具有高保真的特性。
从表3、表5 可以看出,当密信长度为50 000 bit时,本文算法的平均ODG 值相比DE 算法、PEE 算法分别提高了0.479、0.002;当密信长度达到100 000 bit时,本文算法的平均ODG 值相比DE 算法、PEE 算法分别提高了0.595、0.001。对于数据集中的9 种音频,本文算法的ODG 值均能保持一个良好的水平,并且整体上较对比算法有一定幅度的提高。
通过上述对SNR 与ODG 2 个指标的综合分析可以得出:本文算法能够很好地保证音频的感知质量,且对于不同种类的音频具有一定的普适性,在保真度上优于现有的DE 算法、PEE 算法。
5 结束语
DE、PEE 等隐写算法将密信比特以二进制位扩展的方式嵌入到预测误差值中,对载体的修改幅度较大。为此,本文提出一种基于SVO 的音频可逆信息隐写算法,该算法对采样值的修改幅度在[-1,1]之间,具有高保真的特点。同时,本文算法引入采样块复杂度的概念,根据采样块的复杂度实现密信的自适应嵌入。实验结果表明,相对DE 算法和PEE 算法,该算法的SNR 值和ODG 值较高。在嵌密过程中,采样块的大小固定不变,这在一定程度上影响了算法的嵌密容量,因此,设计更合理的分块策略以提高嵌密容量将是下一步的研究方向。
