通过数学模型分析大流行病的特征并建立预警方案

2021-01-15

科海故事博览 2020年8期

（西华大学，四川成都 610039）

1 问题重述

问题一建立数学模型，综合考虑人口数、感染数量、病死人数、疫情持续时间、经济状况、医疗条件、人口密度、防疫政策等因素，给出一个合理的界定“流行”(Epidemic)和“大流行”(Pandemic)病的定量条件。

问题二考虑到无症状感染者具有一定的传染性，且不容易发现，但全民进行病毒检测又成本太高，且时间过长，不利于复工复产，我们试图寻找一种更为有效的方法来最大限度地降低无症状感染者的传播风险，比如对一个地区进行抽样病毒检测来评估该地区的无症状感染者的分布情况，再制定不同的隔离和检测措施。请结合问题一的模型，针对一两个国家（或地区），给出切实可行的病毒检测抽样方案，并给出无症状感染者分布预测模型和针对相应预测结果的应对方案。

问题三给世界卫生组织写一封信，阐述你的团队对于疫情情况的判断，并给出一些防控建议和降低风险的思路。

2 问题分析

2.1 问题1的分析

（1）问题1的实质是结合各种人口指标和治理水平来找到界定流行病与大流行病的相关定量条件以此来真实反映出病毒的传播情况，并能够对于疫情情况给出有效的量化指标，使得疫情能在最佳时间得到良好的控制。为什么要找出这个量化指标呢？首先是为了避免造成不必要的恐慌，因此必须在公布疫情定性标准前，需要对疫情的传播范围、传播速率进行合理的分析。其次量化指标的建立有利于各个国家加强对本国的防护意识，以免疫情的控制大于某个给定的阈值，而发展到不可控或难控的阶段。

（2）各影响因素之间的关系分析。总人口数，其包含了:感染者、易感染者、排出者（因得病死亡或被治愈）。对于感染者的数量，在疫情初期，由于防疫意识没有完全建立，防疫政策没有迅速颁布，其会随着疫情的持续时间迅速上升并达到一个峰值。“经济状况、医疗条件、人口密度、防疫政策”这些因素从客观来讲共同决定了疫情的感染率，因此可利用现有的统计资料和回归方程得出感染率的变化数据依次来找出最佳控制时间段。

（3）流行与大流行的分析。大流行是指某疾病的发病蔓延迅速，涉及地域广，人口比例大，在短时间内可以越过省界甚至洲界形成世界性流行疾病。因此我们在界定大流行和流行的定量条件，可将以上因素作为判断标准，利用微分方程和相频线的分析进行进一步判别。

3 模型假设

在病毒传播期内该地区不考虑人口的变化即总人口数不变；得病后被治愈的人或身亡的人不影响病毒的感染率；假设初期，被感染人数随疫情的发展成指数形式上升；处于潜伏期的患者在一定时间后会出现患病特征成为患病者；新冠肺炎对不同年龄组的感染率略有不同，对健康人的感染率一样；问题二的模型在问题一的模型基础上进行的，所以问题一的模型假设，问题二的模型都满足；以中国为研究国家，在疫情得到控制这段时间内，某地感染者流向其他地区的比例不变,之后近似为与时间呈负相关关系；无症状患者和所有的患者的传染率是一样的；境外输入病历人员的传染率和国内感染者传染率相同；由于每天境外输入人数没有太多规律，每天境外输入病历人数按平均值计算；境外输入病历流向某地的比例也按总体数据计算；我国的境外输入病历是从2月26号开始的，为了方便，我们以下计算都以2月26号为起点计算；各个省份日均治愈率相同。

4 定义与符号说明

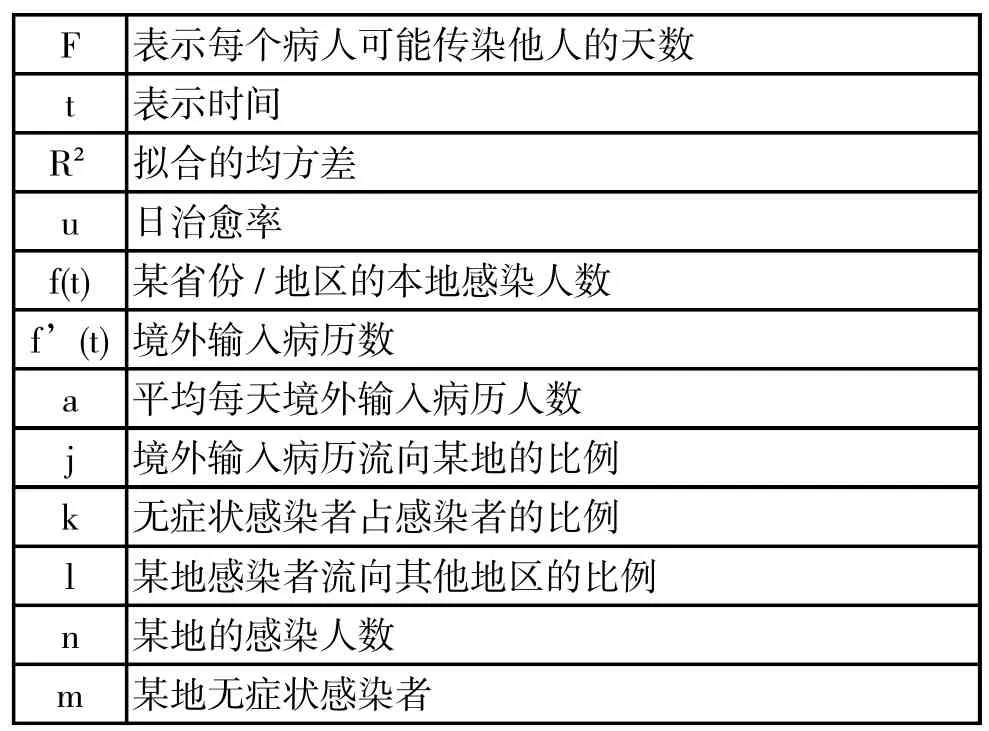
5 模型的建立与求解

5.1 问题一的模型

以我国为例，从1月28号开始，第一例病人出现到2月20达到了峰值，这里我们取k=0.5960，来带入i（t）=i0（1+K）n——①（n为t次方）进行计算，算出累计的确诊人数与实际的患者人数进行比较如图1所示。

从图形中，我们可以看出从1月28日起到2月20日，前22天病人的累计数和我们所用的K=0.5960来代入的数学模型基本上是稳合的，因此我们认为i(t)=i0(1+K)n（n为t次方）是合理的。

在此基础上因为在疫情初期政策的颁布还未下达，人民对疫情的防范意识还不够，因此使得疫情的传播速率极其的快。而后期政府采取了有力的措施，人民的防患意识增强，疫情便会过渡到缓和，其感染率也会逐渐下降，这个时候确诊人数会呈下降趋势，然而一个新的问题便出现了，那就是处于潜伏期的患者可能会造成二次波峰。因此我们采取微分方程的模型对该疫情做出更进一部的分析。

在假设中我们可知：s（t）+i（t）+q（t）+r（t）=1,,利用SIR基础模型建立微分方程组的如下所示：

在前一个模型的基础上我们可以令出K=0.5960，u=0.4，i(0)=0.001，s(0)=0.999，代入方程2利用Matlab编程软件得出“病人、康复者、处潜伏期的人”的变化情况。

对图像进行分，以及计算可知，利用相关轨迹线可知i（t）与s（t）的相关性和基本性质。令W={(s,i)|s≧ 0,i≧0,s+i≦1},对方程组②，因为方程1和方程2与r无关，将两式联立消除dt，并令

但是如果K*u*S0的值＞1，那么疫情将会持续下去，传播范围也就越来越大。因此可分析H随时间的关系图，最终确定疫情传播范围的广泛程度。

5.2 问题二的模型

5.2.1 模型建立

以中国为例，本国的感染者分为本地感染者和境外输入病历，而本地病历最先在武汉发现。根据资料显示，境外输入病历超过百分之七十在隔离期发现，固这部分人中最多只有百分之三十会流向国内。

则湖北的感染人数：1n=f(t)+f’(t)-u1t=ft+0.3atk1-ut

m1=1nj1

再根据资料，我们可以算出每天境外输入病历的平均人数a约=30，(从2月26日境外首次输入病历，至4月18日止计算结果，境外输入总人数参考高校疫情防控平台发布数据)，由问题1的模型得u约为0.02。当k值取0.15时与问题一模型得出的结果基本相同。当j值取0.012时，得出的无症状感染者与实际无症状感染者数量基本相同，以此类推，再计算出其他省份的无症状感染者人数。

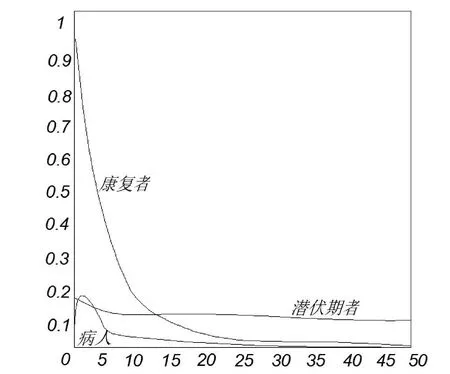
图1

5.2.2 与实际分布对比分析

模型得到的分布图大题上与实际的数据分布图相同，证明了该模型具有一定的预测能力，并可以预测未来一段时间无症状感染者的数量走向，可以为决策者采取措施提供一些参考。

5.2.3 针对相应预测结果的应对方案

政府要求发现无症状阳性检测者时，在2小时内进行网络报告，并进行奖励。各级疾控部门接到辖区内无症状感染者报告时，要求按照新冠肺炎确诊病例调查要求，24小时内完成流行病学调查和密切接触者判定，所有密切接触者一律在所在地集中隔离医学观察14天，管理要求与确诊病例密切接触者相同。

同时，国内限制出入境的条件。如医务人员之类的工作人员和取得通行证并报备的人员可以放行，其他无特殊情况不予以通行。对境外人员，持续开展拉网式全面的摸底排查，在各个入境关道设置检测点，对排查出的境外人员一律开展核酸检测。特殊的，加强对湖北入境人员的健康管理，对湖北人员统一纳入社区管理，及时进行核酸检测。

6 结果分析

6.1 问题一的结果以及模型检验

新冠状病毒在2020年1月中下旬开始在我国爆发，之后在3月4号其它国家如美国、英国、意大利等地也出现了新冠患者，并疯狂的增加，在4月1号达到了一个峰值，并后续在峰值上下波动着。目前已累计确诊215万人，现有确诊人数还有151万人，死亡人数达到了49万人已经远超2009年的新型流感所造成的危害。根有关部门的记录，把疫情期间人流量的登记（并假设境外输入病例算入一个国家最开始的已有患病人数i0）。因此可利用SIR模型：

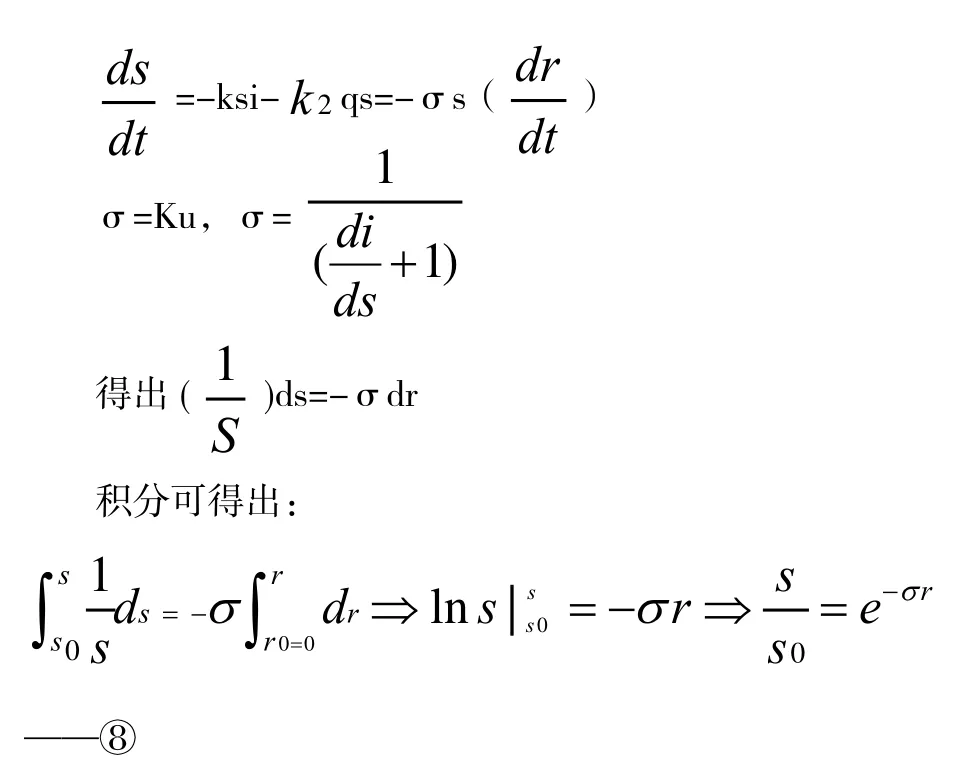
根据H=K*u*s0与1之比找出界定流行与大流行的定量条件。并可算出最佳的处理时间。通过计算出新冠病毒从2月17号（全球正式开始严肃对待）开始（计为0）也是外国病例的初有时期，传染范围指数在不同医疗情况、社会重视程度等……经济条件，随时间的变化趋势如下：与世界到达的到达时间基本相符，且扩大范围H超过了1，因此确立为大流行病，模型验证完毕。

6.2 问题二的结果及模型分析

6.2.1 抽样方案

（1）是对新型冠状病毒肺炎病例的密切接触者开展医学观察期间的主动检测；

（2）是在聚集性疫情调查中开展的主动检测；

（3）是在新型冠状病毒肺炎病例的传染源追踪过程中对暴露人群主动检测；

（4）是对部分有境内外新型冠状病毒肺炎病例持续传播地区的旅行史和居住史人员开展主动检测。

无症状感染者主要是来自于境外输入病例，所以在抽样调查时着重以对输入人员进行检测。

6.2.2 分布预测模型

以中国为例，本国的感染者分为本地感染者和境外输入病历，而本地病历最先在武汉发现。根据资料显示，境外输入病历超过百分之七十在隔离期发现，固这部分人中最多只有百分之三十会流向国内。则湖北的感染人数:

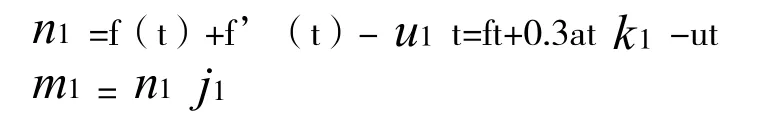
再根据资料,我们可以算出每天境外输入病历的平均人数a约=30，(从2月26日境外首次输入病历，至4月18日止计算结果，境外输入总人数参考高校疫情防控平台发布数据)，由问题1的模型得u约为0.02。当k值取时0.15，与问题一模型得出的结果基本相同。当j值取0.012时，得出的无症状感染者与实际无症状感染者数量基本相同，以此类推，再计算出其他省份的无症状感染者人数。[2]

6.2.3 应对方案