基于群体评价信息集结的中层管理者绩效考评研究 ①

刘 伟， 邱骏达

(1.江苏开放大学商学院，江苏 南京 210036；2.江苏理工学院计算机工程学院，江苏 常州 213001)

0 引 言

在现代企业管理过程中，中层管理者的创新能力和执行能力可以帮助企业提升绩效水平、改善战略品质，这类人群已经成为推动企业发展的中坚力量。中层管理者的绩效考评工作具有复杂性，科学处理考核信息，构建有效的考评体系，有助于公正地评价其综合能力，从而激励他们为企业创造更大的价值。目前，绩效考评理论中应用较多的是关键绩效考核法、目标管理法、平衡计分卡法等[1-4]，采用的数理方法主要有BP人工神经网络法，熵值法以及直觉模糊层次分析法等[5-8]。以往的绩效考评研究多集中在评价者为单一主体，决策数为具体数值的绩效评估，考评的信息相对片面，难以对中层管理者的绩效进行全方位的综合评估。

因此，从多层次、多角度对中层管理者的绩效进行评价，首先利用AHP法确定绩效考评指标以及各评价主体的先验权重。同时，将各评价者的个体评价信息映射到二维平面坐标系中，引入Steiner点的概念，采用模拟植物生长算法(PGSA)求出群体评价的最优信息集结值，并计算评价主体的综合权重，进而求出带权重的综合最优集结评价值，以此对中层管理者进行综合考评。该方法改进了传统平均方法引起的近似集结的现象，提升了群体信息集结的准确性和有效性。

1 研究方法

1.1 区间数判断矩阵的平面点集映射

将各专家给出的区间数判断矩阵映射到二维平面坐标，使得平面坐标上的点与每个专家的决策信息一一对应。对于一个多方案、多属性的群决策问题，e个专家针对m个备选方案，n个属性，给出相应的区间数判断矩阵，则这e个判断矩阵可以映射到二维坐标平面，视为由e个平面所构成的点集：

(1)

k=1,2,…,e

1.2 基于Steiner点的判断矩阵信息集结

事实上，由C(1),C(2),…,C(e)构成的平面点集代表了e个专家的个体偏好，带有权重Wi的e个专家个体偏好信息的最优集结点，恰好即是二维坐标平面点集中的Steiner点。如果能够通过某种算法求解出Steiner点，就可以找到代表群体专家最优决策的信息集结点。

2 基于PGSA的最优集结评价信息求解

2.1 模拟植物生长算法的迭代步骤

模拟植物生长算法是一种受植物向光生长机理启发而提出的智能优化算法[9]，该算法将NP问题的解空间当做是植物的生长环境，其中最优解为光源，在不同光线强度下，植物的枝叶按照设定的角度向着光源快速生长，枝叶快速生长的过程就是寻找全局最优解的过程。与其他优化算法相比较，PGSA有两方面的优势：一方面，PGSA根据枝干上的形态素浓度值确定下一步的寻优方向，且每次迭代的生长点是随机选取的数值，因此能够在较短时间内寻得全局最优解；另一方面，PGSA将目标函数和约束条件分开处理，对参数设置的依赖性较低，无需编码和解码，求得的最优解具有高度稳定性[10]。

若平面上有n个专家偏好信息点S1,S2,…Sn，利用PGSA求解最优集结点的步骤如下：定义一植物的枝干长度为l/1000，其在长度为l的有界闭箱内向东南西北四个方向生长，不断产生新的枝干。

Step1 假设X为n维空间Rn中的有界闭箱，在有界闭箱内有随机均匀的初始生长点am；

Step2 求解各生长点的生长概率：

(2)

Step3 根据以上步骤求得的结果建立在0-1闭区间上的概率空间，以随机数来选择本次迭代生长点am；

Step4 确定步长λ=l/1000，生长点am按照∂=90°旋转，用新的生长点中的局部最优集结点替换am；

Step5 如若不再产生新的生长点且达到设定的迭代次数，得到全局最优解，则停止计算，否则转Step2。

2.2 基于PGSA的专家综合权重的计算

在多属性群决策问题中，“专家权重”反映了每位专家在决策群体中的重要程度。将考评专家权重分为先验权重和后验权重，并根据实际问题将先验权重与后验权重进行合理的组合，从而获得决策过程中专家权重的有效赋权。

2.2.1 先验权重

2.2.2 后验权重

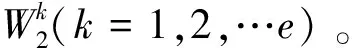
评价主体的决策矩阵越靠近群体最优集结矩阵，说明该主体的估计值偏差越小，估计结果准确。因此，专家权重的客观确定法可以采用离差和最小化的原则：即决策主体所有指标的评价值与对应的群体最优集结评价值的离差和越小，则该评价主体的权重就越大；反之，对应的权重就越小。这样可以避免专家由于主观因素对评价结果造成的估计偏差，对专家权重的赋值也更加合理，从而提高决策的准确性和客观性。

设各决策主体的决策结果矩阵为：

(3)

(4)

群体的决策结果体现了专家共同的意愿，决策结果应趋于一致。即dt的数值应越小越好，最理想的情况下应是零向量[11]。根据离差和最小化原则，定义专家的后验权重的计算公式为：

(5)

2.2.3 综合权重

决策专家的综合权重可以根据先验权重与后验权重的凸组合求得，即设决策专家的综合权重为：

(6)

2.3 基于PGSA的Steiner点求解

考虑到专家权重对于决策结果的影响，采用带有权重的最优集结方法，即解决带有专家权重的Steiner问题。即

minD=

k=1,2,…,e

(7)

式中，D为e个专家到新的最优集结点的加权距离之和。新的最优集结点E**(Steiner点)，同样可以应用PGSA求得，从而得到新的最优集结矩阵：

(8)

3 实证研究

为了验证基于PGSA的群体评价信息集结方法的科学性、有效性，以X公司的相关数据为例，进行了相关理论的实证研究，对中层管理者实施绩效考评。

根据绩效评估指标体系，将影响中层管者绩效的关键因素分层，第一层为中层管理人员绩效评估总指标A，第二层为准则层包括工作业绩、工作态度、工作能力以及管理品质四个因素，即A={B1,B2,B3,B4}，每个准则层又包括4个子准则层，共16个子准则层，即B1={b11,b12,b13,b14}，B2={b21,b22,b23,b24}，B3={b31,b32,b33,b34}，B4={b41,b42,b43,b44}，如表1。

3.1 基于AHP法的权重的计算

层次分析法(AHP)最早是由美国运筹学家Saaty提出的，是一种将定性与定量有机结合的多层次群决策方法。运用AHP确定中层管理人员绩效评估指标的权重具有一定的合理性。

表1 中层管理者绩效考核指标体系

3.1.1 各层次属性权重的计算

由于本文的重点在于运用PGSA对专家评价信息的综合集结，因此对于AHP求权重的具体步骤并不一一描述。定义准则层权重集为：

W=(w1,w2,w3,w4)

子准则层权重集为：

W1=(w11,w12,w13,w14),W2=(w21,w22,w23,w24),

W3=(w31,w32,w33,w34),W4=(w41,w42,w43,w44)

则根据AHP法，得出中层管理者绩效考核各级指标权重如下：

W=(0.4586,0.1432,0.3048,0.0934),

W1=(0.5462,0.2323,0.0838,0.1377),

W2=(0.1091,0.3509,0.1891,0.3509),

W3=(0.5086,0.1342,0.2949,0.0622),

W4=(0.5376,0.2430,0.0699,0.1494)

3.1.2 专家先验权重的计算

中层管理者工作范围较广，与企业内外各个层面都有广泛的接触，因此本文从上级、同事、下级、本人以及客户五个层次对其进行全面性的评价。但由于不同层面评价者对被评价者的具体情况了解程度不同，同时每个层次对管理者的工作要求也所有不同，因此我们需要确定每个层次的决策者权重，以增加绩效评估结果的全面性与科学性。

本文从上级，同事，下级，本人，客户五个层面，共选取了12位评价者对被评价者进行绩效考评。则根据AHP法可以得出五大评价主体的先验权重如下：

3.2 基于PGSA的绩效评价信息集结

从工作业绩、工作态度、工作能力以及管理品质4个一级指标及16个二级指标，分别按照优秀(90-100)、良好(80-89)、中等(70-79)、合格(60-69)以及不合格(0-59)五个等级对被评价者进行绩效评价。

3.2.1 判断矩阵的映射

将“优秀”、“良好”、“中等”、“及格”和“不及格”转化为对应熟知的区间数[90,100],[80,89],[70,79],[60,69],[0,59]，并根据判断矩阵映射公式(1)，将五个评价主体的评价结果转化为空间中对应的点(90,100),(80,89),(70,79),(60,69),(0,59)。则上级、同事、下级、本人以及客户五个评价主体对四个一级指标的员工初始评价值M=(mij)p×q综合分析结果如下：

3.2.2 群体最优集结评价值的求解

根据初始点M=(mij)p×q，利用模拟植物生长算法，得到的群体最优集结评价值S*=(sij)m×n：

3.2.3 决策主体综合权重的计算

根据各评价主体给出的初始评价矩阵及群体最优集结评价矩阵的偏离程度，由公式(5)，可以得出五大评价主体的后验权重分别为：

根据公式(6)，取λ=0.5，则五大主体的综合权重赋值如下：

W1=0.2646,W2=0.4434,W3=0.0801,

W4=0.1324,W5=0.0795

则五大主体的先验权重、后验权重及综合权重如表2所示。

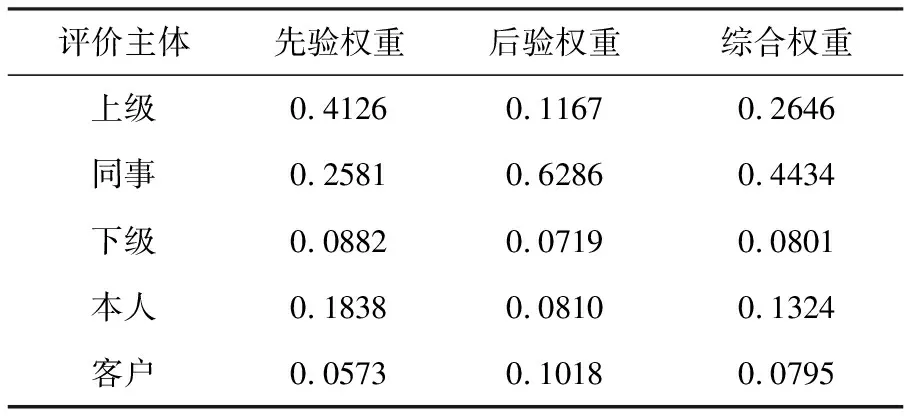
表2 五大评价主体的综合权重

3.2.4 综合最优集结评价值的求解

将五大评价主体的综合权重与其初始评价矩阵相结合，得出带专家权重的综合最优集结评价矩阵：

3.2.5 绩效评价结果的确定

根据以上步骤得到的各级属性权重及综合最优集结值，得出该中层管理人员综合评价值，如表3。

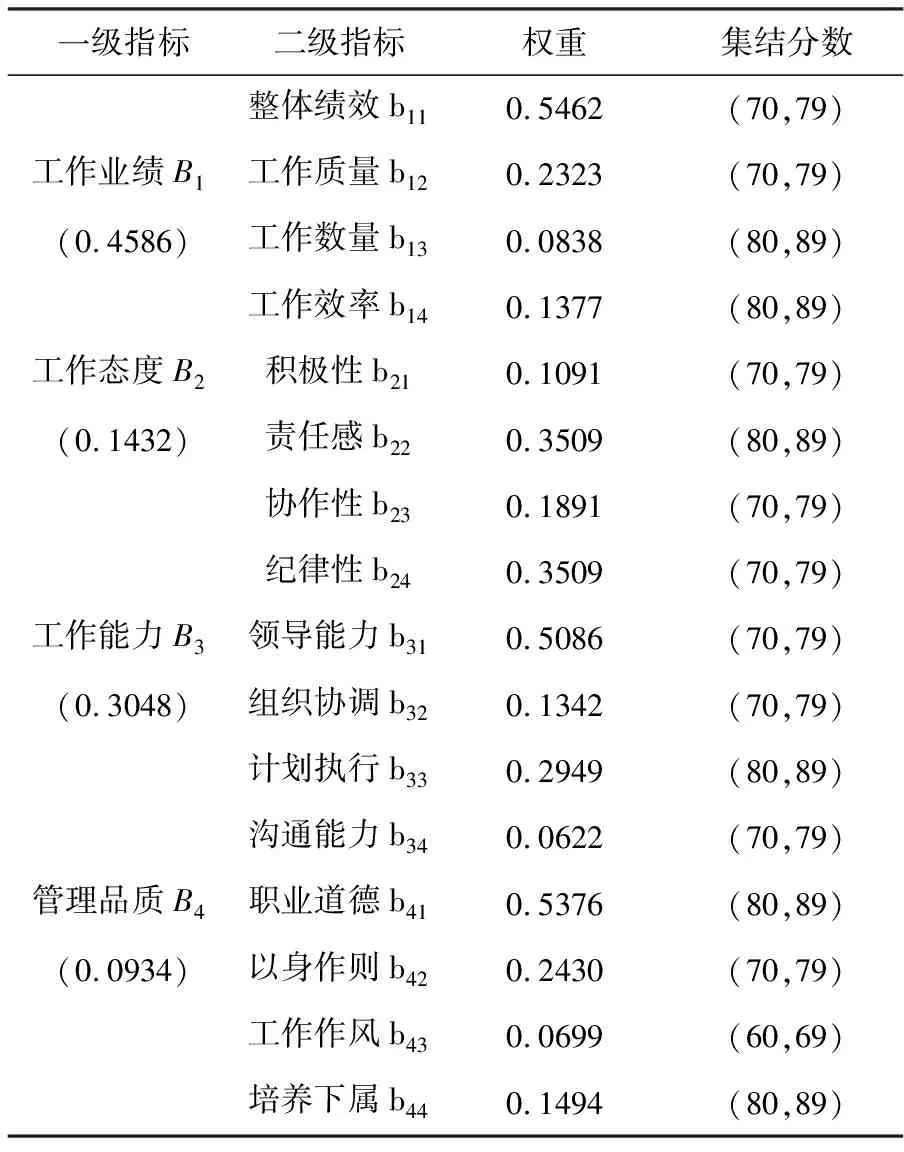
表3 中层管理人员综合评价值

首先对每个一级指标模块进行综合评价，从表3可以看出：

S1=[(70,79)(70,79)(80,89)(80,89)]

又因为

WB1=(0.5462,0.2323,0.0838,0.1377)T，

B1=S1×WB1。

通过加权平均得到该管理人员的工作业绩的综合评价B1=75.72，处于“中等”等级。同理，该管理人员的工作态度综合评价B2=78.01，处于“中等”等级；工作能力的综合评价B3=77.44，处于“中等”等级；管理品质的综合评价B4=80.66，处于“良好”等级。

而该中层管理人员的整体绩效：

A=B×WA，

B=[B1,B2,B3,B4]=[75.72,78.01,77.44,80.66]，

WA=(0.4586,0.1432,0.3048,0.0934)T

则该管理人员的最终整体绩效为77.03，处于“中等”等级。同时，如果一个员工的全部绩效以100% 计算，也说明该中层管理人员只发挥了其全部绩效的77.03%。在绩效考核中，企业可以通过对上述各模块及综合分析的结果的分析，了解中层管理者的绩效薄弱环节，有针对性的提出改善措施，以使其充分发挥个人绩效，为企业创造最大价值；同时，考评结果也是对中层管理者进行奖惩的重要依据。

4 结 论

根据X公司的实际经营情况建立了中层管理者的绩效考核体系。通过将专家判断矩阵映射到平面点集，引入Steiner点的概念，采用PGSA算法找到专家评价信息的最优集结点，从而得到最优信息集结矩阵。同时根据评价主体的评价矩阵与最优信息集结矩阵的偏离程度求出评价主体的的综合权重。最后计算出中层管理者的综合评价值，为中层管理者绩效考核提供了一种新的方法。