基于通用学习字典的机织物纹理表征
2021-01-15李立轻
占 竹 王 凯 李立轻 汪 军
(东华大学,上海,201620)
纹理反映了物体表面的信息。由于机织物特殊的形成方式,机织物纹理具有一定的周期性,并且随着原料的种类、织物密度以及织物组织结构等参数的不同呈现出复杂多变的特性。研究机织物纹理,使用字典学习方法对机织物纹理图像进行重构,不仅可以去除图像采集过程中的噪声,而且可用于疵点检测、织物密度检测和织物组织结构识别等方面,因此织物纹理的表征分析具有重要意义。
字典学习算法的主要目的是用于图像的重建,其目标是构建一个最小化训练样本重构误差的字典。ENGAN K 等[1]提出 MOD 算法,该算法通过使重建误差最小化来学习得到一个重建能力更强的字典,用l0约束稀疏编码来使获得的稀疏编码尽可能稀疏。AHARON M 等[2]提出 K-SVD字典学习算法,该算法釆用奇异值分解的方法来依次更新字典中的每个原子,并在更新原子的过程中也更新与之相对应的稀疏编码,以此来加快收敛速度。WANG J 等[3]提出的字典学习算法用局部性来代替稀疏性,因为局部性能保证稀疏性,反之不行,作者只使用与训练样本最接近的k个字典原子的线性组合来重构训练样本,以此来学习得到一个能体现局部性的字典。这些字典学习算法所构造的字典只包含某一类图像的特征,对其他类别的图像重构效果并不理想。本研究提出通用字典学习方法构造出包含多种织物纹理特征的学习字典,进而实现了对不同种类机织物纹理的有效表征。
1 字典的构造
字典的来源一般有两种,一种是直接预定义的固定字典,它是由固定的数学函数构造出来,并不包含某一特定纹理的特征,但是通过合理地选择数学函数构造字典,可以实现纹理图像的良好表征;另一种则是学习字典,以机织物等纹理图像为样本,通过机器学习算法,剔除了机织物纹理中的一些冗余信息而获得的主要纹理特征。对于字典的生成速度,固定字典的算法简单,构造速度相对较快,而学习字典的算法复杂繁琐,构造速度慢。
1.1 固定字典
通过字典元素的线性组合可以实现对样本的最优近似。固定字典通过合理地选择数学函数,其一般具有近似大多数样本的能力,例如通过离散余弦变换(Discrete Cosine Transform,DCT)构造 DCT 字 典[4],利 用 Gabor 变 换 构 造 Gabor 字典[5],利用小波变换构造小波字典[6]。当构造出字典以后,对纹理的重构可以看成一个线性规划问题,只需要求解出相应的系数,将字典和系数作矩阵的乘法就可以得到对原图像的重构图像。
DCT 字典是由离散余弦变换产生的余弦积构成的,当给定信号f(x),x=1,2,…,N-1,其离散余弦变换见式(1)和式(2)。
式中:F(u)是第u个余弦变换系数,u是广义频率变量,u=1,2,3,…,N-1。具体而言,要得到一个尺寸为m2×n2的二维可分离DCT 字典,首先构造一个m×n的一维DCT 矩阵D1D。其中第k个原子由1,2,…,n,i=1,2,…,m给出。然后除第一个原子以外的所有原子减去它们的平均值,最后得到的DCT 字典是由矩阵张量积D2D=D1D⊗D1D计算得到,当处理二维图象时矩阵具有可分离性。
1.2 学习字典
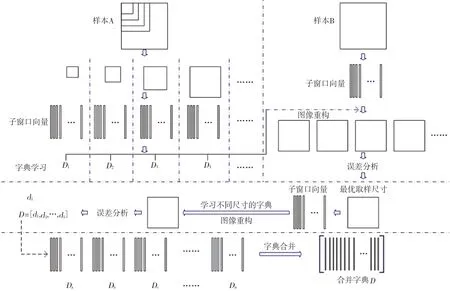
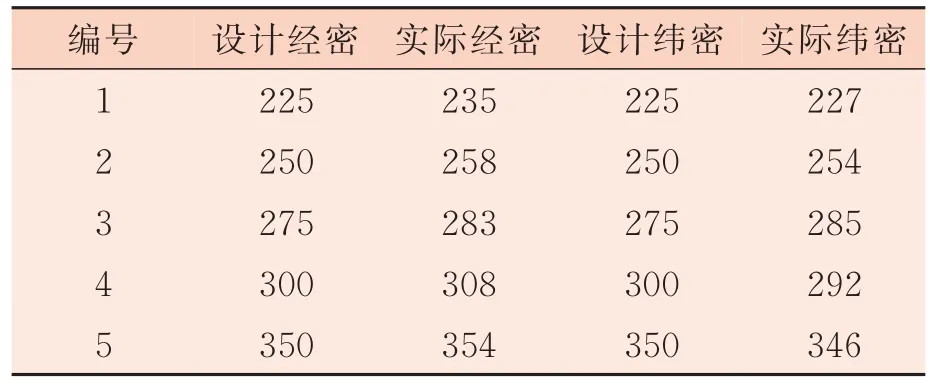
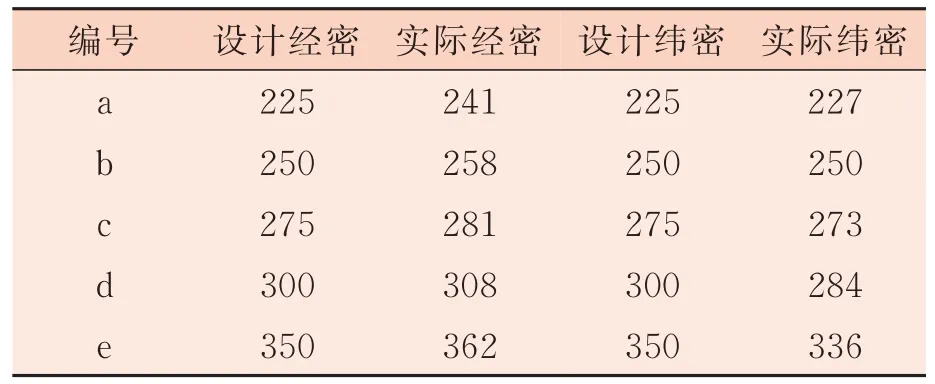
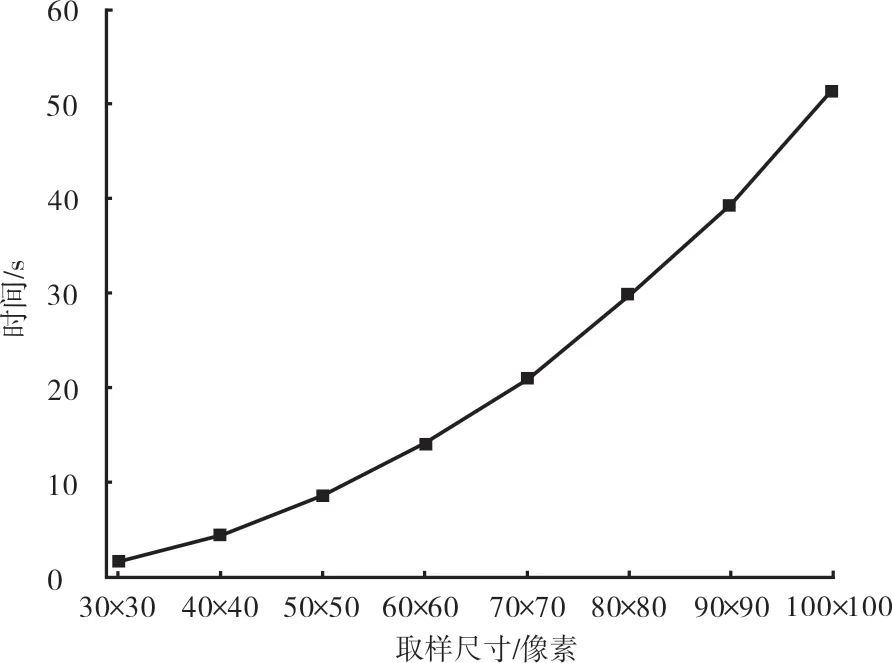
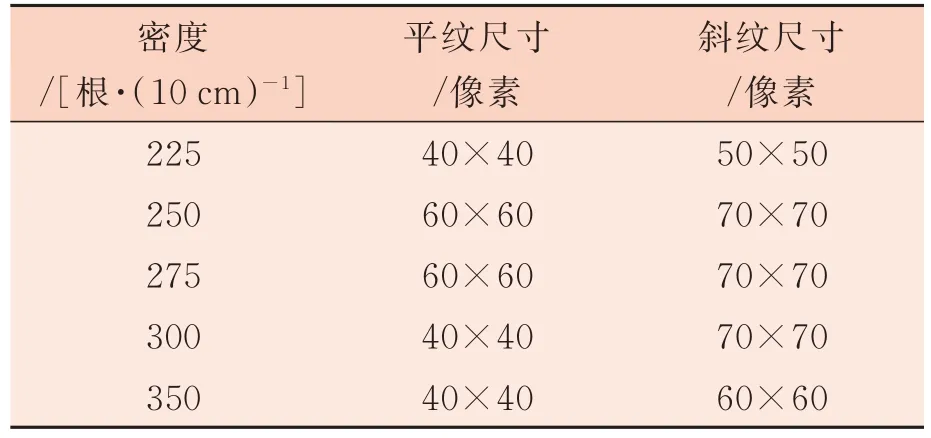
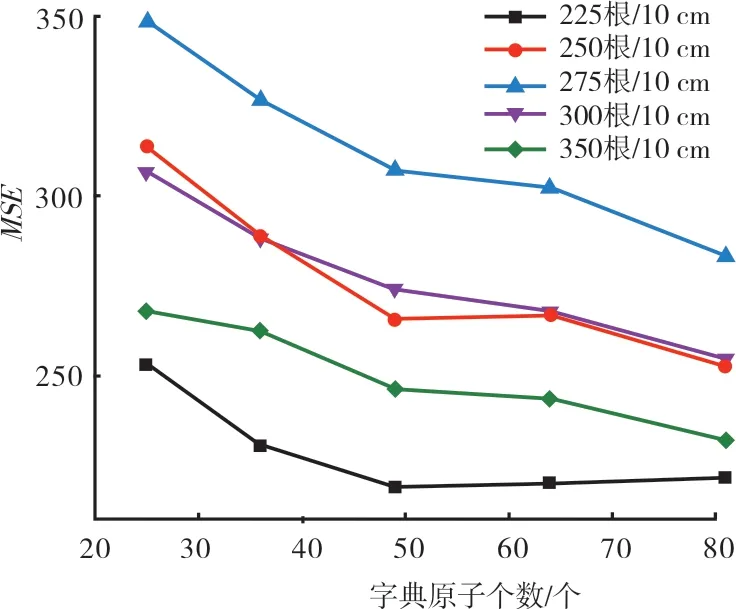
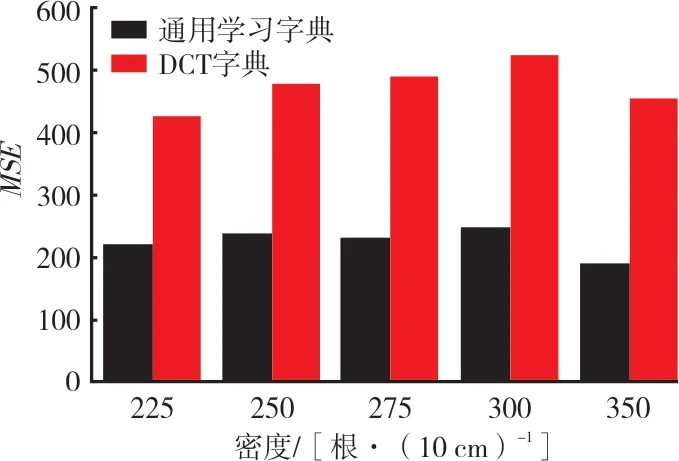
字典学习方法是近几年非常流行的一个超完备字典构造方法[7-8],其核心是利用已有的训练样本来学习得到一组自适应的基向量,该基向量应能够满足重构误差和稀疏度的要求。令学习字典字典D中 的每一列dK∈Rn称为一个原子,样本数据矩阵X=设A是X在字典D上的编码系数矩阵,记为即X≈DA,如果αi中仅有T0(T0< 式中:X表示样本数据矩阵;D为所要学习的字典;A为所对应的系数矩阵;T0为字典D的稀疏度。 K-SVD 算法是无监督字典学习中的一种经典算法,其已经成功应用于图像处理领域,包括图像重构和图像去噪[9-13]。K-SVD 算法的目标是学习得到一个过完备的字典,其通过交叉迭代更新稀疏编码和字典,最终获得一个表示能力强的过完备字典。K-SVD 算法字典更新过程中采用SVD 分解依次更新字典原子,在更新原子的同时也更新与之相对应的稀疏编码,从而加速收敛,稀疏编码阶段采用OMP 贪心跟踪算法进行求解[14]。 构造包含多种织物纹理特征的通用学习字典,优先需要考虑的两个问题是每一种织物的取样尺寸和提取的字典原子个数在保证重构质量的前提下要尽可能小。这是因为机织物纹理具有周期性,过多的样本量并不会对提高最终重构图像的质量有显著帮助,但却会显著增加通用学习字典构造的时间,合理地选择字典的大小也可以提高算法的效率。 通用学习字典构造算法流程图如图1 所示。 图1 通用学习字典构造算法流程图 对于每一种织物,提取同一块织物样本不同区域128 像素×128 像素尺寸的图像分别记为样本A 和样本B,样本A 和样本B 应该具有相同的纹理特征。以不同的取样尺寸在样本A 中选取不同数量的子样本,使用经典的K-SVD 字典学习算法计算得到不同样本量条件下的学习字典,分别使用这些字典去重构样本B,计算重构图像与原图像之间的均方误差MSE、峰值信噪比PSNR和相关系数R等指标,根据图像重构质量和算法所消耗的时间确定该种织物图像的取样尺寸。在确定取样尺寸基础上,选取不同字典原子个数学习得到不同大小的字典,使用这些字典对样本B进行重构,优选出其中重构图像质量好的字典原子个数。最后将不同织物学习得到的字典列向合并,就可以得到一个包含多种织物纹理特征的通用字典,该字典具有更好的通用性。其中,均方误差、峰值信噪比和相关系数均为客观评价重构图像和原图像近似效果的指标,其定义分别见式(4)、式(5)和式(6)。 式 中 :I代 表M×N的 原 始 灰 度 图 像是 图像I的近似图像为Frobenius-范数(矩阵中所有元素绝对值的平方和再开平方),n为每像素的比特数,一般取8,即像素灰阶数为256,Cov(I,I^)为I与I^的协方差,Var(I)为I的方差,Var(I^)为I^的方差。由以上公式可知,MSE值越大,PSNR值越小,相关系数R值越大,重构图像I与原始图像I^近似效果越好。 本研究所用样布均为全棉白织坯布,使用纱线为18.22 tex 精梳棉纱,在TNY101B-20 型全自动剑杆小样织机上设计织制了5 块不同密度的平纹样本和5 块不同密度的二上一下右斜纹样本,表1 和表2 列出了详细的设计规格参数。采用佳能9000F MarkⅡ型扫描仪采集织物样本图像,为了增加图像的对比度,在织物背面放置一块全黑的硬纸板。所采集到的样本图像皆为8 位灰度图像,灰度值为0~255 之间的整数,其中0 代表颜色为纯黑,255 代表颜色为纯白,图像尺寸为256 像素×256 像素,分辨率为600 dpi。不同密度平纹和斜纹织物样本原图如图2 所示,其中第1 行为平纹,第2行为斜纹,编号与表1 和表2 一一对应。 图2 不同密度平纹和斜纹织物样本 表1 平纹织物样本规格参数 单位:根/10 cm 表2 斜纹织物样本规格参数 单位:根/10 cm 本研究的试验基于MATLAB R2014a(64 位)软件开发环境,计算机配置INTEL CPU(2.3 GHz)和4 G 内存。为了确定每个织物样本所需的最小取样尺寸,按照本研究第2 节算法所述,从样本 A 中分别截取 30 像素×30 像素、40 像素 ×40 像 素 、50 像 素 ×50 像 素 和 60 像 素 ×60 像素一直到100 像素×100 像素等不同尺寸的图像,使用有重叠的16 像素×16 像素子窗口在截取图像上按水平和垂直方向每间隔1 个像素滑动,分别可以得到 225、625、1 225、…、7 225 个子样本,定义初始字典的尺寸为256×100,选择MSE值作为图像重构评价指标。 取样尺寸对不同密度平纹和斜纹织物图像重构误差的影响如图3 和图4 所示。可以看出随着训练样本取样尺寸的增加,重构图像的误差明显减小,当取样尺寸超过一定大小之后,再增加取样尺寸,重构误差减小趋势放缓。这是因为当取样尺寸达到某一临界值后,从训练样本内能够提取出几乎所有表征该织物的纹理特征,再增加取样量并不会对重构结果产生显著影响。 取样尺寸对学习字典生成时间的影响如图5所示。可以看出,随着取样尺寸的增大,构造学习字典的时间呈上升的趋势。 综合考虑图像重构质量和字典构造时间两个指标,以重构图像误差显著放缓的点作为各个密度织物样本图像的最优取样尺寸,取样尺寸结果见表3。 图3 取样尺寸对不同密度平纹织物图像重构误差的影响 图4 取样尺寸对不同密度斜纹织物图像重构误差的影响 图5 取样尺寸对学习字典生成时时间的影响 表3 不同密度平纹和斜纹织物样本取样尺寸 根据1.2 节对字典中原子的定义,字典原子个数即为学习得到的字典中列向量的个数。根据表3 对不同密度的织物图像选择对应的取样尺寸,选取的字典原子个数分别为 25、36、49、64 和81,训练得到字典,使用这些字典分别对样本B 进行重构,重构误差如图6 和图7 所示。 可以发现,不管是平纹织物还是斜纹织物,几乎都是在字典原子个数为49 时重构误差减小放缓或者出现最小值。这是因为过大的字典中存在冗余信息,反而不利于织物纹理的重构,因此对于所有样本设定的字典原子个数都为49。 图6 字典原子个数对不同密度平纹织物图像重构误差的影响 图7 字典原子个数对不同密度斜纹织物图像重构误差的影响 通过以上分析,每一块织物样本图像通过KSVD 字典学习算法可以得到大小为256×49 的学习字典,该字典包含对应密度织物纹理的主要特征,将这5 种密度的字典进行合并将会得到同时包含这5 种不同密度织物纹理特征,大小为256×245 的通用学习字典,如图8 所示。可以看出,通用学习字典中包含了原始织物的纹理结构信息。 图8 不同密度织物通用学习字典 DCT 字典和通用学习字典对不同密度斜纹织物图像的重构误差如图9 所示。DCT 字典的重构误差仍然比通用学习字典的重构误差大,说明该通用学习字典既具备了对多种不同密度织物的通用性,同时其重构性能也要比DCT 字典更好。 图9 DCT 字典和通用学习字典对不同密度斜纹织物图像的重构误差 本研究以不同织物密度平纹和斜纹样本为例,详细介绍了通用学习字典构造算法并应用于机织物纹理表征,确定了不同样本的最优取样尺寸和重构该样本纹理所需的最优字典个数,并比较了通用学习字典和DCT 字典对多种织物纹理图像的重构质量。试验结果表明,通用学习字典可以实现对不同种织物纹理的重构,且其重构性能明显优于DCT 字典,但是其泛化性能还有待进一步研究。
2 通用学习字典构造算法
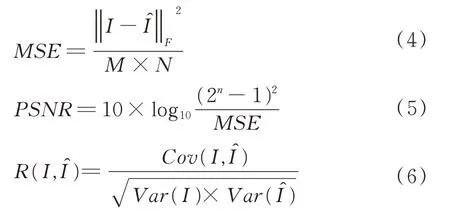
3 试验结果与分析
3.1 样本的获取

3.2 不同密度样本取样尺寸分析


3.3 不同密度样本字典大小分析

3.4 通用学习字典的重构效果验证

4 结论
