基于层次隐马尔可夫模型和神经网络的个性化推荐算法
2021-01-15郭聃
郭 聃
(四川现代职业学院电子信息技术系 四川 成都 610207)
0 引 言
个性化推荐系统现已成为电子商务、电影娱乐业以及新闻媒体领域中一个必不可少的部分,推荐系统不仅能够提高用户的浏览效率,而且能够为服务提供商带来经济效益[1]。协同过滤推荐系统是当前最为成功且应用最为广泛的一种推荐系统模型,但目前的推荐系统领域主要关注于解决用户评分的稀疏性问题和冷启动问题[2],将提高推荐的准确率作为首要目标,而忽略了用户的多样性和个性化特点[3]。
电子商务等领域中普遍存在长尾分布的现象[4],推荐系统更倾向于将“热门”项目推荐给用户,这会影响用户的满意度,也不利于服务提供商扩大经济收益。此外,对指定用户的推荐结果常常集中于少数的一些候选项目,导致推荐结果的排序成为用户满意度的又一个关键因素[5]。因此提高推荐的多样性和个性化是一个极有意义的研究方向,近期也得到了研究人员的广泛关注。文献[6]基于用户浏览的历史记录和当前的上下文场景为用户提供多样化的推荐列表。文献[7]设计了两阶段的推荐方法,第一阶段预测并补充稀疏的用户评分,第二阶段对协同过滤推荐的结果进行排序处理。目前提高推荐多样性的主流方法都是通过显式评分信息产生推荐列表,然后通过排序算法产生个性化的项目排序,这种方法所产生项目列表的多样性依然有提高的空间[8]。
用户和项目的大多数交互均为隐式信息,例如:音乐应用的用户极少对音乐给出显式评价,但是听同一首音乐的次数、听音乐的时间点和播放时长等隐式信息的价值甚至高于显式的评分信息[9]。本文充分考虑用户和项目交互的隐式信息,设计了一种基于层次隐马尔可夫模型的上下文预测算法,基于预测的上下文产生对应的推荐项目集。此外,设计了神经网络来求解协同过滤的推荐问题,其满足贝叶斯个性化排序[10]的条件,因此神经网络输出的推荐结果经过了个性化的排序处理。
1 推荐系统的问题模型
设U={1,2,…,N}为一个用户集,I={1,2,…,M}为一个项目集,交互数据集为S⊂U×I,(u,i)∈S表示用户u和项目i的交互,正反馈记为(u,i)∈S,负反馈记为(u,i)∈(U×I)-S,正反馈和负反馈包含的项目分别称为正项目和负项目,设Iu+表示用户u的正项目集,Iu-表示用户u的负项目集。
Iu+={i∈I:(u,i)∈S}
(1)
Iu-={i∈I:(u,i)∈(U×I)-S}
(2)
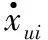
xuij=xui-xuj
(3)
式中:xuij表示对xui和xuj喜好的程度差异。
本文对用户进行个性化项目排序,目标是最大化用户正负项目i∈Iu+和j∈Iu-的概率,采用ROC曲线的AUC作为度量方法:
(4)
式中:H(·)为Heaviside函数。AUC值越接近1,性能越好。
2 层次隐马尔可夫模型
推荐系统考虑的上下文主要包括时间上下文、地理上下文、社交上下文和模式上下文,模式挖掘是最常见的上下文感知方式,但在项目数量多或者数据稀疏性高的情况下,推荐的准确率较低。本文设计了两层隐马尔可夫模型(Hidden Markov Modeling,HMM)[11]自动学习每个用户的潜在上下文,将上下文作为状态(隐变量),用户喜好的项目为观测量,学习的目标包括估计状态的转移概率、每个观测量的概率分布以及状态变化所引起的用户上下文变化,利用这些潜在状态表示用户的上下文。
2.1 总体结构
每个上下文建模为一个隐藏变量,检测用户喜好之间的相同上下文模式,根据这些模式预测用户的下一个上下文。包含两层隐藏变量,将用户对项目的正反馈序列作为训练第1层的观测序列,第1层的隐藏变量作为训练第2层的观测序列。第1层隐藏变量表示了用户关于时间的潜在上下文,第2层隐藏变量提取了不同上下文状态之间的相同模式。图1为本文HMM的结构图。
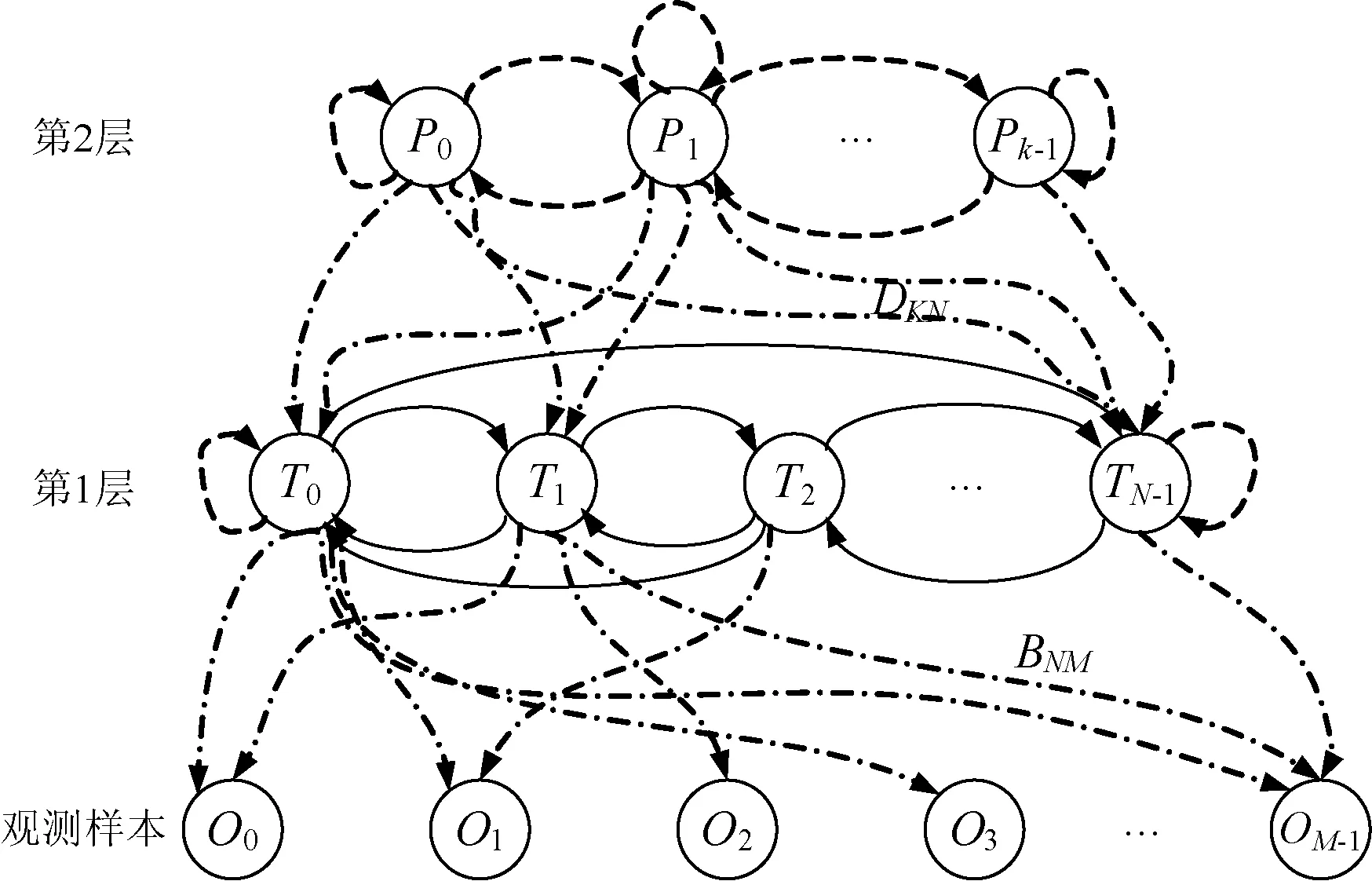
图1 层次隐马尔可夫模型的两层结构
2.2 推断过程
将HMM模型的参数表示为λ(A,B,C,D,π),N为第1层的状态量,M为项目(观测变量)的数量,A为第1层的状态转移概率,B为隐藏状态和项目之间在第1层的观测概率矩阵,C为第2层的状态转移概率,D为第2层和第1层之间的观测概率矩阵,π为初始化状态分布,设O=(O0,O1,…,OL-1)表示长度为L的观测序列,Oi表示从用户收到反馈的第i个项目。基于HMM的推荐系统需要解决以下3个核心问题:1) 计算观测序列的似然;2) 计算概率最大的状态序列;3) 估计HMM模型的参数。
直接计算问题1)需要约2L×NL次乘法运算,所以采用前向算法来减少问题的复杂度:
αl(i)=P(O0,O1,…,Ol,xl=si|λ)
(5)
式中:l为时间戳;αl(i)为在l的观测序列概率;si为马尔可夫过程的状态。
(6)
采用前向算法需要约L×N2次乘法运算,小于直接计算的运算量。
采用后向算法解决问题2):
βl(i)=P(Ol+1,Ol+2,…,OL-1|xl=si,λ)
(7)
式中:递归计算αl(i)和βl(i)。对于所有的观测变量和状态,定义以下的关系:
γl(i)=P(xl=si|O,λ)
(8)
αl(i)度量了时间l之前的相关概率,βl(i)度量了时间l之后的相关概率。状态序列的概率定义为:
(9)
根据γl(i)的定义,时间戳l可能性最高的状态是最大化γl(i)的状态si。
问题3)的解决方法是将矩阵的大小固定,然后确定合适的矩阵元素:
γl(i,j)=P(xl=si,xl+1=sj|O,λ)
(10)
(11)
(12)
2.3 基于HMM产生推荐列表
算法1是基于两层隐马尔可夫模型的上下文感知推荐算法。
算法1基于HMM的推荐算法
1.随机初始化HMM的模型参数λ(A,B,C,D,π);
2.for each 用户udo
3. for each用户反馈信息
4. 基于给定的观测序列重新估计参数λ(A,B,π);
5. 基于观测序列计算第1层的状态序列;
6. 基于第1层状态序列重新估计参数λ(C,D,π);
7. 基于第1层序列计算第2层的状态序列;
8. 基于λ(C,D,π)预测下一个上下文;
9. 基于λ(A,B,C,D,π)预测下一个项目;
10. end for
11.end for
HMM第1层:收集每个用户的反馈序列,首先更新矩阵A和B,更新每个序列第1层的转移概率矩阵和观测概率矩阵。然后寻找第1层中似然最大的状态序列,该序列等价于该用户上下文状态最相似的转移概率序列,使用Viterbi算法[12]寻找最优的隐状态序列。根据第1层发现的序列更新矩阵C和D,再根据观测的项目序列重新估计参数A和B。
HMM第2层:通过最大似然决定第2层的状态序列,该序列是第2层隐藏变量中最可能发生转移的序列,所以该序列反映了上下文的变化。基于训练的上下文转移概率(参数C和D),预测用户的下一个上下文。给定预测的上下文和观测概率矩阵B,推导出和预测上下文匹配的推荐列表。
在模型训练完成之后,将矩阵C和D相乘,预测用户的下一个上下文。然后,将矩阵A和B相乘,计算每个项目被推荐的概率。最终,基于计算的概率和预测的上下文,生成上下文对应的top-N推荐项目。层次隐马尔可夫模型的总体程序流程如图2所示。
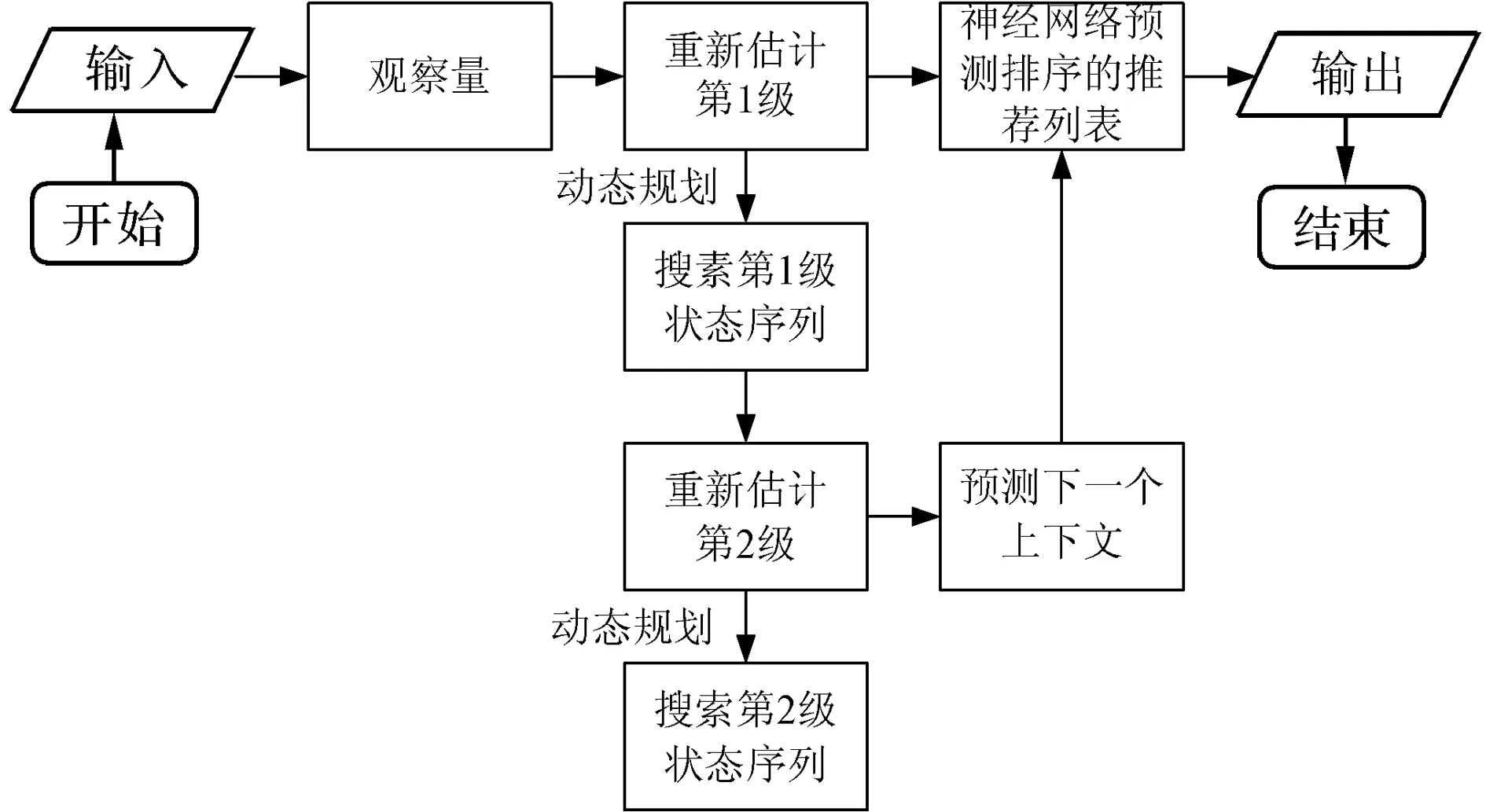
图2 层次隐马尔可夫模型的上下文学习流程图
3 基于神经网络的个性化排序模型
3.1 网络结构设计
本文网络模型是多层前馈神经网络结构,共有四层:用户层L1、隐藏层L2、项目层L3和排序层L4,如图3所示。L1层神经元数量和用户数量相等,L3层神经元数量和项目数量相等,L2层神经元数量K决定了用户和项目的规模。
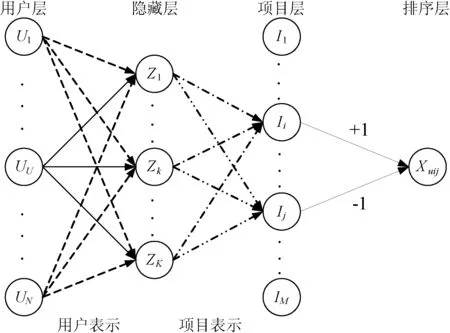
图3 本文的多层前馈神经网络结构
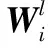
3.2 前向传播
设R={(u,i,j)|u∈U,i∈Iu+,j∈Iu-}为训练样本集。网络采用二进制形式表示每个用户:a1∈{0,1}N,表示为指示向量形式(z0,z1,…,zN), 如果j=u,则zj=1,否则zj=0。隐层L2的输出a2相应变为:
(13)
(14)
式中:k=1,2,…,K表示隐层的神经元;函数f:RR为隐层的激活函数。a2和f之间存在以下的关系:
(15)
(16)
(17)
采用Sigmoid函数σ作为排序层的激活函数,比较用户u对于项目i和项目j的喜好程度。
3.3 后向传播
采用交叉熵C作为网络的代价函数:
(18)
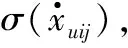
(19)
激活权重W的更新规则定义为:
W←W+αΔW
(20)
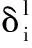
企业价值共创体系的涌现指由价值情报探测及分析系统、协调控制系统、协同生产系统等构成的企业价值共创体系整体所具有的超越各组成系统的能力。借鉴穆勒提出的判断涌现存在与否的三个判据[21]:可加性判据、新奇性判据和可演绎性判据[22-23],将企业价值共创体系的涌现分为两个层次:第一个层次是价值共创体系继承与各组成系统的能力,但其能力指标不是系统级能力指标的简单线性叠加,而是非线性的整体价值创造能力的改变值。第二个层次是价值共创体系具备的而单个体系组成系统并不具备的价值创造能力,表现在体系的整体价值创造能力指标上。
(21)
(22)
(23)
后向传播引起如下的权重变化:
(24)
(25)
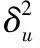
(26)
最终更新用户层u的激活神经元,因为网络的输入为1u,所以用户u的权重增量为:
(27)
3.4 Mini batch处理
本文神经网络同时处理一批样本,设一个Mini batch的样本量为p,从U中随机选择p个用户,随机选择每个用户的正项目和负项目,训练程序每次迭代中处理一个Mini patch。
3.5 偏置层
协同过滤的矩阵分解模型在预测评分的程序中引入偏置项,有助于提高预测的准确性,并且能够加快训练的速度。偏置项将评分预测划分为多个元素:用户-项目-交互项、用户偏置、项目偏置和全局偏置,用户偏置和项目偏置可理解为全局偏置的平均偏差。
本文增加一个偏置层,该层聚集所有的偏置项,偏置层位于项目层和排序层之间,根据相关的偏置项修改项目层的激活值。修改式(16)可获得偏置层的输出:
(28)
(29)
式中:bg表示全局偏置;bU为用户偏置;bI为项目偏置。排序层的输出变为:
(30)
4 神经网络和贝叶斯个性化排序的关系分析
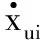
(31)
(32)
贝叶斯个性化排序(Bayesian Personalized Ranking,BPR)表示为:
(33)
式中:Θ表示所有的模型参数。推导矩阵分解模型的所有权重,可获得:
(34)
(35)
式中:p为用户权重;q为项目权重。
根据文献[13]的分析和结论,本文的神经网络实现了贝叶斯个性化排序的效果。
5 实 验
5.1 网络模型的实现方式和参数设定
本文实验的操作系统为Ubuntu 16.04,基于Pytorch verson 0.4.1实现本文的神经网络模型,Pytorch能够完全占用GPU来加速模型的训练过程,实验采用Nvidia Quadro M6000的GPU,GPU训练一个epoch的速度大约是32核CPU的5倍。采用Pytorch缺省的L2正则化和Adam优化器实时更新神经网络的权重。
实验中对Aadm优化器的学习率、隐层神经元数量和批大小3个超参数进行专门的调节,其他超参数采用Pytorch的缺省值。超参数的优化步骤为:人工设置初始化的超参数;设计局部搜索算法进行优化处理。局部搜索算法的具体过程为:选择一个参数,随机将该参数增大或者减小10%,如果网络的AUC性能得以提升,则持续该参数的变化方式;如果性能下降,则进行相反的变化方式,重复10次,选择其中性能最好的两个参数值。实验发现参数值的差异较小,最终学习率设为0.01,隐藏层的神经元数量设为K=100,批大小为500。
5.2 实验数据集和对比方法
采用Netflix数据集作为benchmark数据集,该数据集共包含100 480 507个评分、17 770部电影和480 189名用户。数据集也含有用户对电影评分的时间戳。
选择4个与本文接近的推荐系统作为对比,分别为:(1) 基于隐马尔可夫模型的推荐系统[14],简称为HMM。本文也采用隐马尔可夫模型对上下文进行建模和预测,以验证本文方法的上下文预测效果。(2) 基于模式挖掘的推荐系统[15],简称为Pattern Mining。模式挖掘是一种常用的多样性推荐系统,该方法用来验证本文方法的多样性效果。(3) 基于贝叶斯个性化排序和矩阵分解的推荐系统[16],简称为BPRMF。贝叶斯个性化排序是一种经典的个性化排序模型,本文的神经网络也满足贝叶斯个性化排序的条件,用来验证本文方法的个性化推荐效果。(4) 基于k近邻的推荐系统[17],简称为KNN。KNN是一种以推荐准确率为首要目标的推荐系统,是目前最常见的推荐系统类型。
5.3 性能评价指标
采用了推荐系统领域常用的3个性能指标评价推荐结果的准确性,分别为精度(P)、召回率(R)和F1-measure(Fm)。分别统计了top-5和top-10推荐结果的准确性。
采用流形偏置方法[18]评价推荐结果的多样性,该方法将项目集按照频率排序,然后均匀分为10个bin,同一个bin内项目的流形度相似。
5.4 推荐准确率实验
图4和图5分别为各算法top-5和top-10的推荐结果。HMM、Pattern Mining、BPRMF系统的推荐准确率均高于KNN算法,KNN算法仅考虑了用户评分的相似性,而本文benchmark数据集的评分数据稀疏性较大,所以KNN的准确率较低。HMM、Pattern Mining、BPRMF系统均考虑了数据的潜在信息和上下文信息,因此其推荐精度、召回率和F1-measure略优于KNN算法。本文方法设计了上下文预测机制,充分利用了benchmark数据集的时间戳信息,并且对推荐列表进行了个性化的排序,所以取得了较好的推荐准确性。
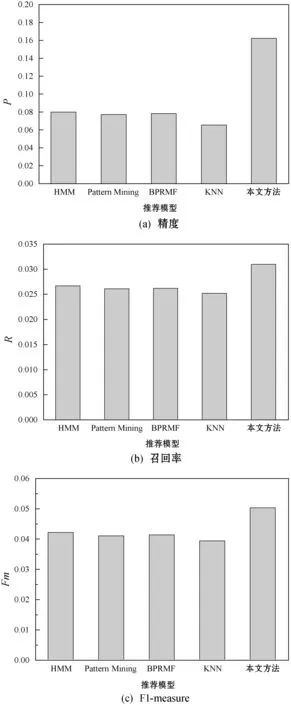
图4 top-5推荐的准确率结果

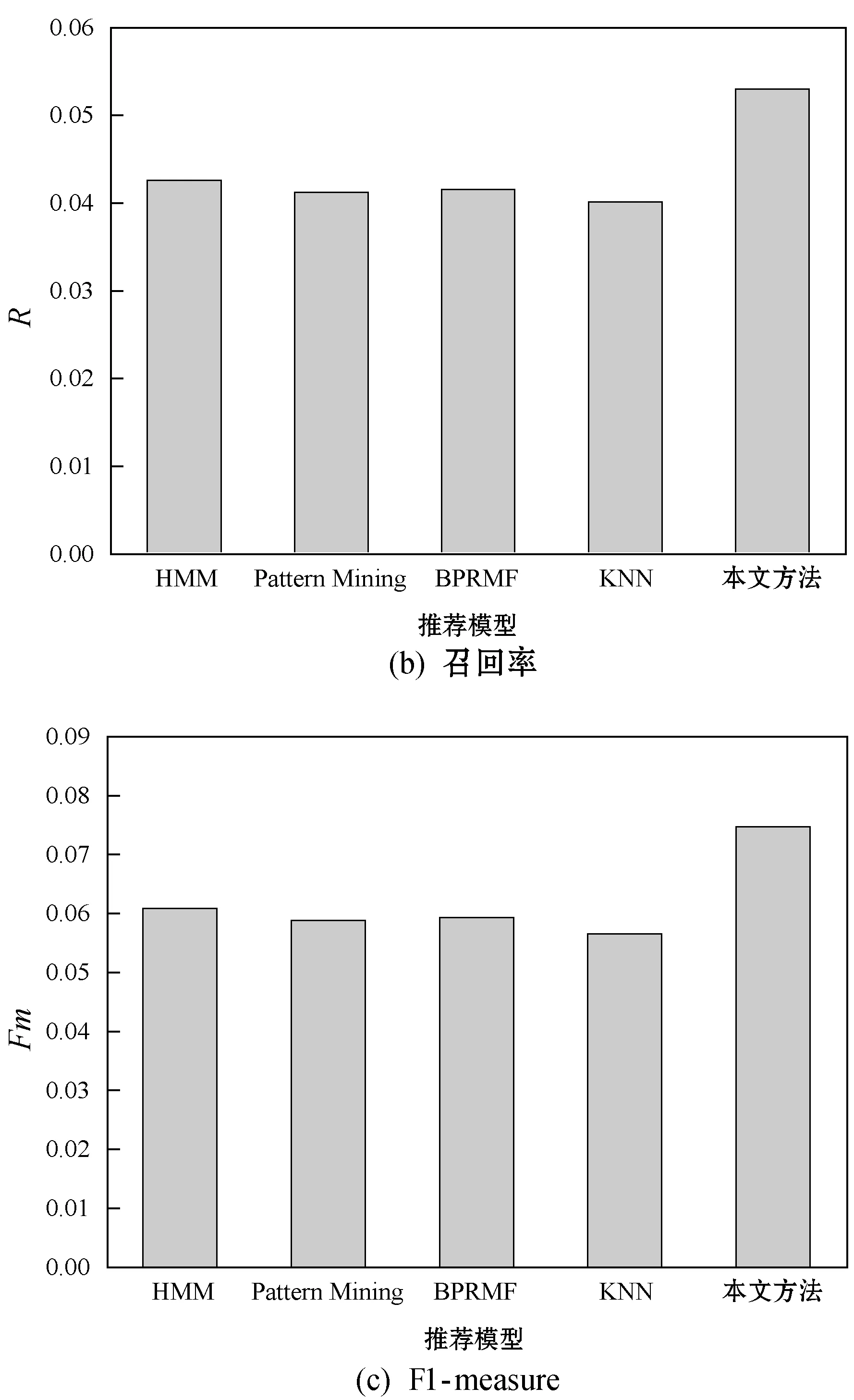
图5 top-10推荐的准确率结果
5.5 多样性实验
图6比较了本文方法和其他推荐系统的多样性。可以看出,KNN的推荐项目全部为最流行的10%项目,多样性较差;HMM考虑了数据的隐式反馈信息和上下文环境,其推荐多样性好于Pattern Mining和BPRMF。而本文方法的推荐多样性好于HMM算法,并且明显考虑了长尾分布的项目,实现了较好的推荐多样性。
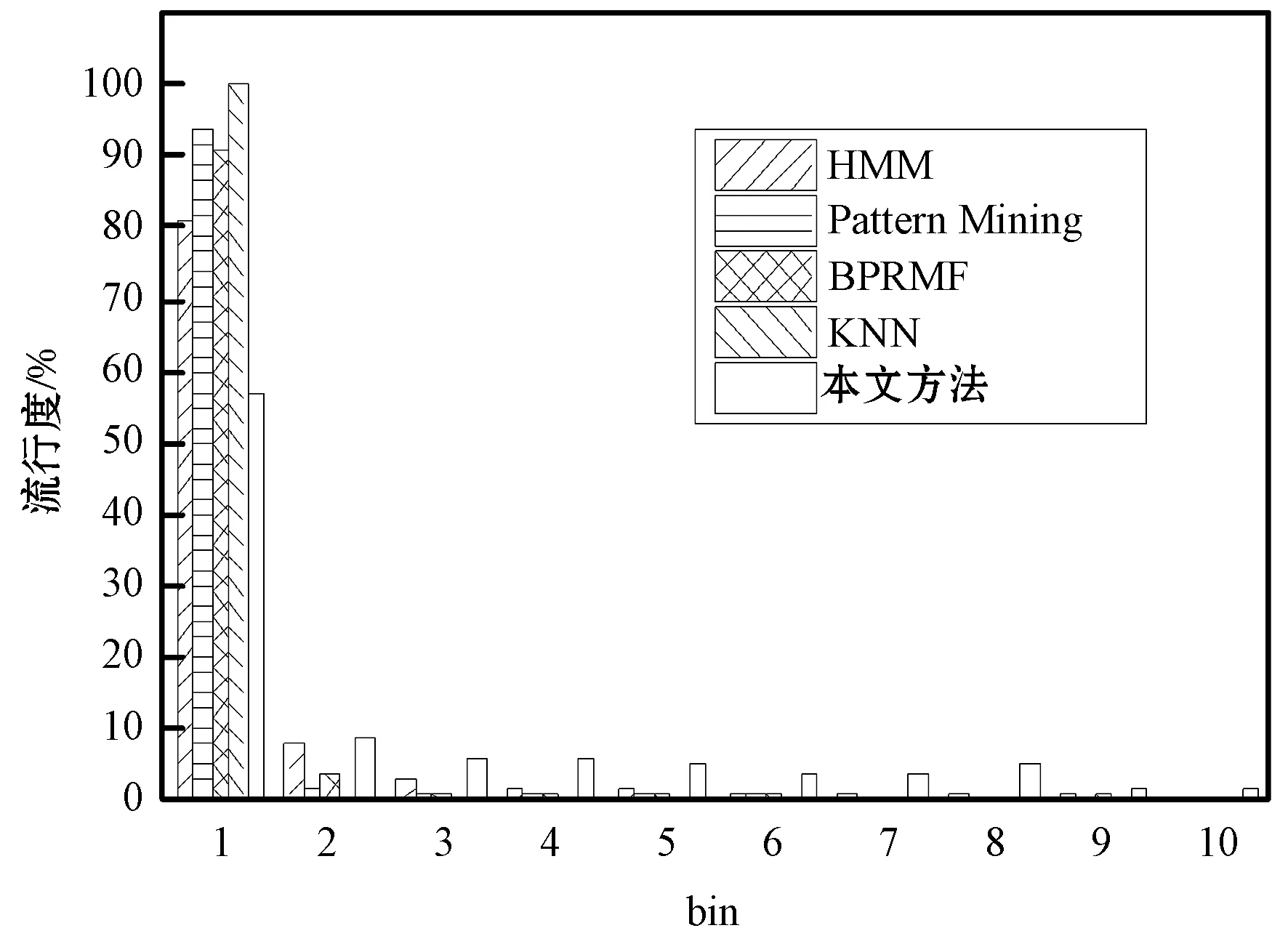
图6 推荐多样性结果比较
5.6 个性化实验
因为Pattern Mining和KNN两个算法并未考虑推荐结果的排序处理,所以仅将本文算法和HMM、BPRMFL两个包含个性化排序的算法比较,结果如图7所示。HMM系统将推荐准确率作为主优化目标,将AUC作为次优化目标,其AUC结果低于BPRMFL算法。BPRMFL则采用矩阵分解实现了个性化排序,其结果优于HMM系统。本文方法采用神经网络实现了个性化排序的目标,取得了最佳的个性化结果,其原因在于神经网络的学习能力强于一般的矩阵分解技术。
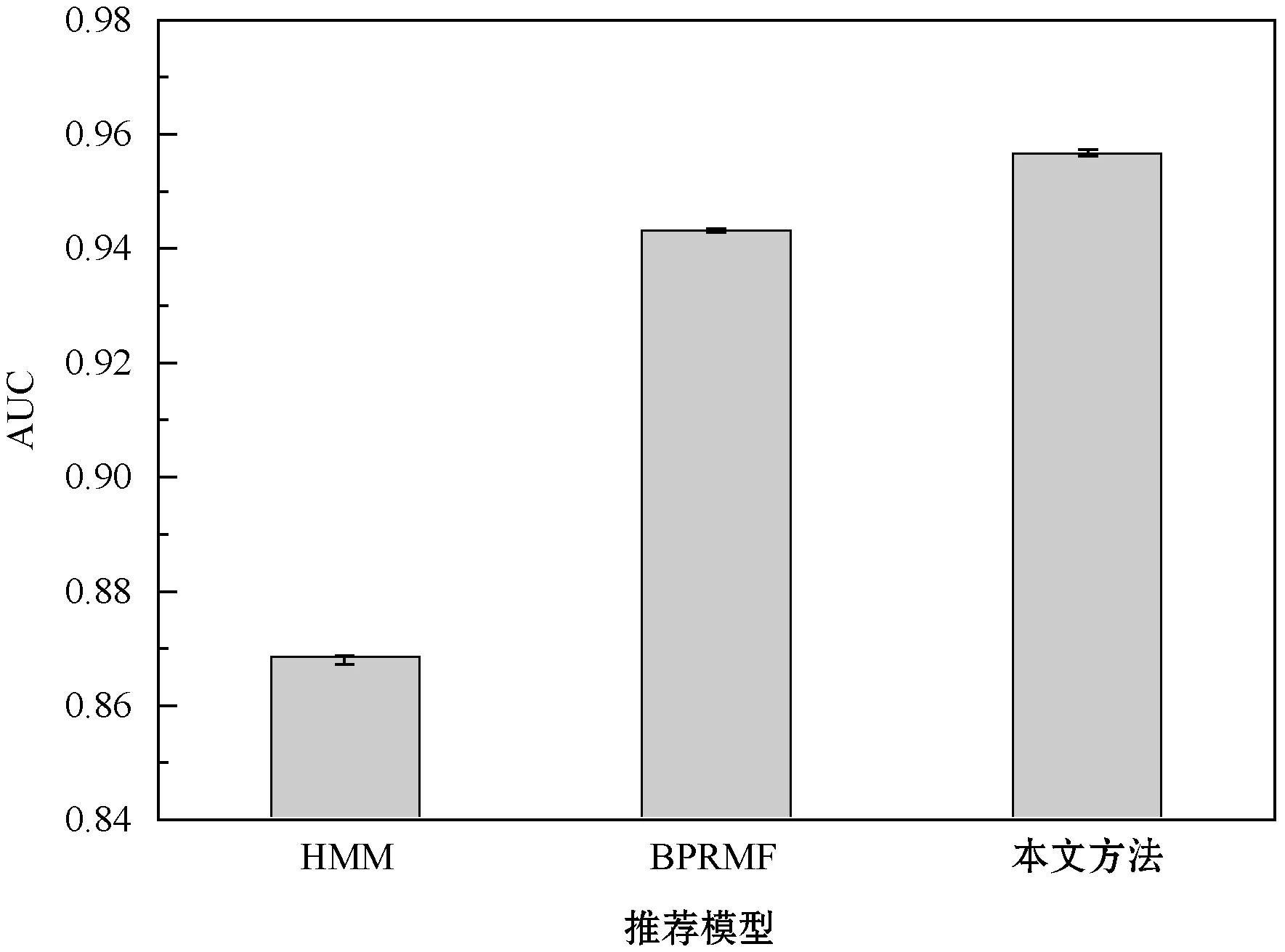
图7 推荐系统的个性化排序结果
6 结 语
本文采用两层的隐马尔可夫模型对推荐系统的上下文建模,设计了上下文的预测和推荐方法,再利用神经网络较强的学习能力,实现对推荐结果的个性化排序。基于层次隐马尔可夫模型建模用户在不同上下文的喜好变化,学习每个用户状态转移的最大似然,根据概率分布预测用户的下一个上下文,并产生预测上下文的推荐列表。此外,基于神经网络实现了个性化排序,其结果优于矩阵分解的个性化排序方法。实验结果证明,本文在保持较高推荐准确性的前提下,实现了较高的推荐多样性和个性化。
