Spark平台环境下基于Aco-k means算法的滚轴故障检测算法研究
2021-01-15刘兴建原振文
刘兴建 原振文
1(广东工商职业技术大学计算机应用技术系 广东 肇庆 526040) 2(国防科技大学炮兵学院 湖南 长沙 410111)
0 引 言
当前工业产业和工业技术的飞速发展,使旋转设备的应用领域逐渐扩大,并开始拓展到了航天、交通、电力、电子等诸多关键的高科技产业部门[1-2]。与此同时,旋转机械设备应用范围的持续扩大,对设备本身性能的稳定性提出了更高的要求。旋转机械设备在使用过程中的寿命曲线呈现出逐渐降低的趋势,由于机械设备少量磨损到完全失效是一个相对漫长的过程,频繁更换关键零部件也会显著增加设备的使用成本,因此最为有效的方式是对旋转设备整体和关键零部件的工作状态进行监控[3-4]。由于大型旋转设备的工作环境大都十分恶劣,对关键部件的连接可靠性及零部件本身的磨损情况具有极高的要求,如果关键零部件出现故障,会造成严重的工程事故和经济损失。滚动轴承是旋转机械设备中最为关键的零部件之一[5],其工作的稳定性将关系到整个设备能否安全运行[6]。如果能够采取有效方法预测出滚动轴承是否存在故障隐患,将会在很大程度上避免安全事故的发生。
关于旋转设备中滚动轴承的故障预测问题,已经成为当前国内外机械自动化领域的一个研究热点问题。文献[7]提出一种基于中值滤波和小波去噪相结合的故障预测方法,但该种预测方法过于复杂,不易操作,且预测精度和可靠性都较低。文献[8]从压缩感知的视角出发,基于信号集的变化提取滚动轴承的振动信息,但该种算法的实际可行性和适用性与理论上存在差距。文献[9]提出一种智能SVM与PCA相结合的故障预测算法研究,引入一种振动信号降维的处理理念,但该种方法仅针对少量集中故障类型有效,在算法分类和全局寻优的过程中易陷入局部最优解。大数据和云计算技术在机械故障检测中的应用已经成为一种发展趋势,尤其是Spark平台的应用,为海量故障信息的提取和处理提供了一种新的模式。本文在大数据的环境下基于Spark和蚁群k类均值聚类算法(Ant Colony System-kmeans clustering algorithm,Aco-k means)提出了一种用于滚动轴承故障预测的方法,利用Aco-k means算法在数据聚类和全局寻优中的优势,可以显著提高对滚动轴承故障预测的精度和预测效率。
1 算法总体设计
由于滚动轴承的摩擦力很小[10-11],因此在旋转设备中有较为广泛的应用,导致滚动轴承出现故障和失效的原因很多,如金属疲劳、进入异物、轴承腐蚀、轴承过载等。滚动轴承在正常工作中会发生振动,此时发生振动的频率为设备的固有频率。一旦滚动轴承发生故障,轴体与故障点发生接触,滚动轴承的振动频率也会发生相应的变化[12],这种频率上的变化是判定故障类别和故障程度的一个重要指标。由于轴承的正常磨损而发生的振动频率变化与故障变化存在差别,可以利用Spark平台环境下的大数据引擎,提取和分析待检测滚动轴承的故障特征,并基于Aco-k means算法在数据聚类分析中和全局寻优中的优势,实现对故障程度的准确定位。Spark平台是大数据产业发展到一定阶段的产物,是一种开源的数据计算框架,由于该平台采用了多节点的计算模式,因此能够在短时间内识别出滚轴数据集合的不同特征,进而识别出滚轴发生故障的严重程度,Spark平台基础框架结构如图1所示。
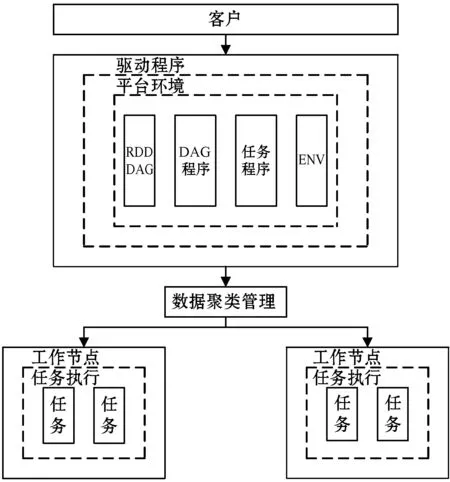
图1 Spark平台的框架结构
此外,Spark平台所应用的弹性数据集可以帮助用户实现代码转换,将提取到的故障数据集投影到平台工作节点的随机运行内存中(Random Access Memory,RAM),便于后续的数据调用和读取。由此可见,Spark平台强大的数据分析和处理功能,可以有效应对海量的滚动轴承故障数据集分析。Spark平台还具有极高的软件兼容性,能够与其他开源软件实现无缝对接[13-14],Spark平台支持市面上主流的计算机算法和计算机语言,能够为数据处理提供统一的解决方案,从而省去了大量的磁盘操作时间,能够提高对滚动轴承故障数据的识别和处理效率。Spark平台采用了弹性分布数据集(Resilient Distributed Datasets,RDD)内存计算模式,具有强大的数据迭代处理能力,增强了系统的执行速度。k means算法是故障数据聚类分析中的常用算法之一,但该方法对于样本集合中的孤立数据较为敏感[15],容易陷入局部最优解。Aco算法应用仿生学的原理对故障数据的特征项进行全局寻优,将两种算法相结合,能够最大限度地减少聚类中孤立数据点所产生的不利影响[16],提高对滚动轴承故障数据聚类分析的准确性,算法总体的流程设计如下:
Step1提取旋转设备滚动轴承工作中的时频域特征数据集,并对数据集做降维处理。
Step2对种群数据集进行初始化处理,并获取降维处理的候选故障数据集。
Step3确定聚类中心的数量及样本数据间的欧氏距离,并基于蚁群算法优化聚类中心。
Step4获取新的聚类中心及数据集合的边界,确定算法的收敛性能。
Step5基于滚动轴承故障特征聚类分析结果,最终确定旋转设备是否存在故障风险。
2 滚动轴承故障时频域特征提取
判断旋转设备滚动轴承的工作状态和故障状态,主要依靠采集到的振动信号,但该类设备的工作环境往往十分恶劣和复杂,因此提取到的振动信号往往不具有线性分布特征,而且还包含大量的环境噪声,稳定性极差。振动信号的特征提取,将会对性能评估构成重要的影响,因此传统单纯的时域振动特征提取与频域振动特征提取方法,都无法准确地提取到设备的振动特征,为此本文采用时频域相结合的提取振动故障特征数据集,进而分析滚动轴承的故障严重程度。滚动轴承发生故障时,瞬时振动状态和突变振动状态中都包含着高频率畸变故障特征,因此采用小波包变换的方法分解振动信号中的高频部分,既可以保持高频信号中的瞬态特征,又可以兼顾低频信号的特征。设提取到的滚动轴承振动原始信号为x(t),用小波变换函数η(t)和正交函数κ(t)递推及提取原始信号中的故障时频域特征,递推关系过程可以表示为:
(1)
式中:y(i)和z(i)分别为高低频滤波系数。两者表达式如下:
(2)
式中:y(i)和z(i)满足关系z(i)=(-1)iy(1-i)。将式(1)的应用范围扩展进行拓展,当i=0时,有η(t)=ζ0(t)、κ(t)=ζ1(t),则有:
(3)
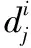
(4)
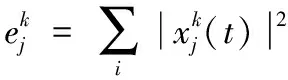
x″(t)=C×x(t)
(5)
对包含频带能量时域特征信号进行聚类处理,获取候选的节点数据集,以精确地确定旋转设备滚轴轴承的故障类别及程度。
3 滚轴轴承故障特征聚类分析
包含时频域特征的故障信号具有海量性的特征,而Spark平台的应用,为海量滚轴故障信息的提取和处理提供了一种新的模式。对原始的信号特征种群进行初始化处理,从降维处理后的滚动轴承特征数据样本集合x″(t)中随机选取h个对象作为数据的原始聚类中心,开始对全部的样本振动信号数据进行聚类处理,将数据对象按照其本身的特征分配到最适合的类别当中,进而计算出滚动轴承故障数据对象距离聚类中心的平均值,在计算过程中会存在平方误差。因此数据聚类的过程是一个反复迭代寻优的过程,不断地循环操作这一步骤,直到将故障预测误差控制在最小的区间之内。
在传统k means数据聚类算法中,常用数据间的欧氏距离来衡量和判断数据之间的相似度,以便对时频域特征相似的数据进行聚类处理。设滚动轴承特征数据样本集合x″(t)中的任两个数据a和b,满足条件a,b∈xi,则a和b之间的欧氏距离D(a,b)可以表示为:
(6)
分别设nq和mq为第q类故障数据中的样本数据与样本均值,则与欧氏距离相关的数据聚类平方误差准则函数f(D)可以表示为:
(7)
由于k means数据聚类算法数据迭代寻优的过程中对于初选值具有较高的依赖性,因此极容易陷入局部范围的最优,使滚动轴承故障预测结果出现偏差,为此本文在传统k means算法的基础上引入了Aco仿生算法,在全局范围内迭代寻优,提高k means数据聚类算法的鲁棒性。基于Aco仿生算法优化样本数据集的聚类中心,设样本数据集合中的初始故障数据特征对象xi∈x″(t),滚动轴承故障数据的聚集可视为一个半径为r的圆形区域,用函数γ(xi,r)表示以xi为中心,r为半径的区域内的故障数据数量,经Aco仿生算法优化后的聚类中心数量r(xi)可以表示为:
r(xi)=γ(xi,R)≥ζ
(8)
式中:R=[maxr(xp,xq)]/2;ζ为样本数据集开平方根函数,ζ=sqrt(h)。传统k means数据聚类算法下,滚动轴承的故障数据开始围绕着h个原始聚类中心,聚类中心可能会借助孤立的数据点表示,进而在故障特征数据聚集的过程中陷入局部最优解,影响最终的聚类效果。而引入Aco仿生算法后,能够优化原有的聚类中心,避免了传统k means算法下随机选择聚类中心,而给选择设备滚动轴承的故障预测带来不利的影响。
设χq和ωχ第q故障数据集的上逼近集与权重比例,ξq和ωζ为第q故障数据集的边界集和权重比例,则经过Aco仿生算法优化后的故障数据剧烈中心h′可以表示为:
(9)
按照Aco-k means算法优化聚类中心后,再以新的聚类中心及故障特征数据与聚类中心间的欧氏距离重新进行全局范围内的聚类划分,有助于显著提高聚类精度。同时基于最大最小原则,采用动态调整的模式调整滚动轴承故障数据簇的数量及与新聚类中心的距离,并求解出每一个故障数据簇中的上逼近集χq和边界集ξq。对在Aco-k means算法下得到的经过优化的聚类中心记性循环迭代,并逐渐调节参数,判断算法的收敛性能,最后,算法结束时获得全局最优解,准确识别出滚动轴承的故障特征与故障程度。
4 实 验
4.1 仿真实验环境设置
为验证提出旋转设备滚动轴承故障预测方法的性能,搭建仿真实验环境,仿真实验台由底座部分、步进电机、主轴、皮带、轴承等部分组成,如图2所示。

图2 滚轴故障测试实验平台组成
实验过程中系统模拟真实的工作情况,旋转动力经由步进电机与皮带向主轴系统传递,滚动轴承被安装在主轴的另一端,配备了各类传感器监控故障信号的变化情况,故障振动测试台的相关参数与测试用滚动轴承的相关参数如表1和表2所示。
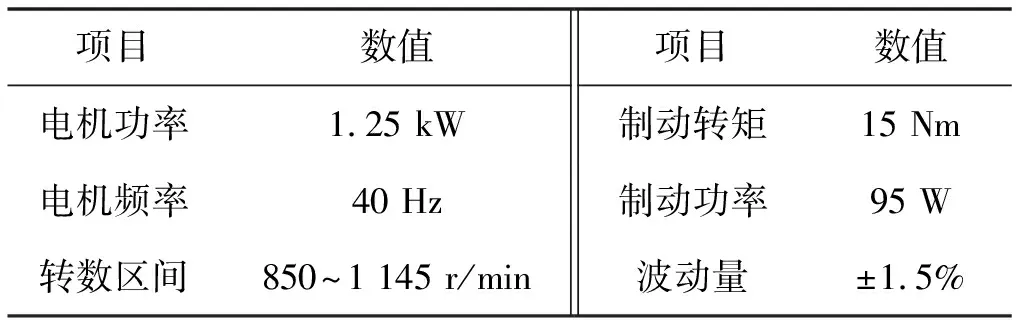
表1 滚动轴承故障测试台相关参数
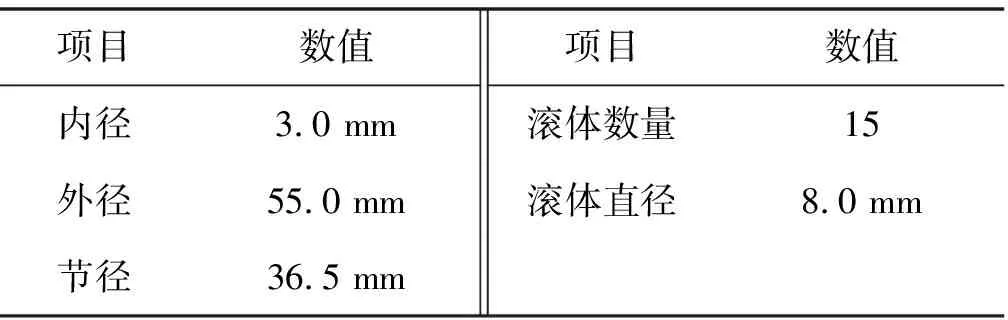
表2 实验用户滚动轴承的相关参数
本文的部分参考比较数据来自凯斯西储大学的滚动轴承的基准数据库中,其提供了不同参数条件下轴承运动和轴承故障的基础测试数据,在表1和表2的条件下从仿真实验台采集了一组样本数据,并以同等条件下西储大学的测试数据区间为标准,剔除奇异样本数据和标准差超出范围的异常数据,最终确定出实验所用故障数据样本数量为25 200个,样本长度为128。基于MATLAB 8.0软件对实验采集到的数据进行分析,在大数据的仿真环境下,为验证提出基于Spark平台和Aco-k means算法的滚动轴承预测算法的有效性,对提起的故障特征数据样本进行训练,测试提出方法的效率、预测准确率和信号解调谱的变化情况。
4.2 方法故障预测计算效率与复杂度对比
在滚动轴承故障检测过程中,故障数据集具有海量性的特征,因此预测方法的计算效率指标十分重要。用500个故障数据节点模拟既定比例条件下的数据聚类效果,并分析滚动轴承故障数据的寻优情况,能够成功识别到50个有效数据节点即可。分别引入文献[8]和文献[9]方法进行对比验证,三种方法的计算效率对比结果如图3所示。
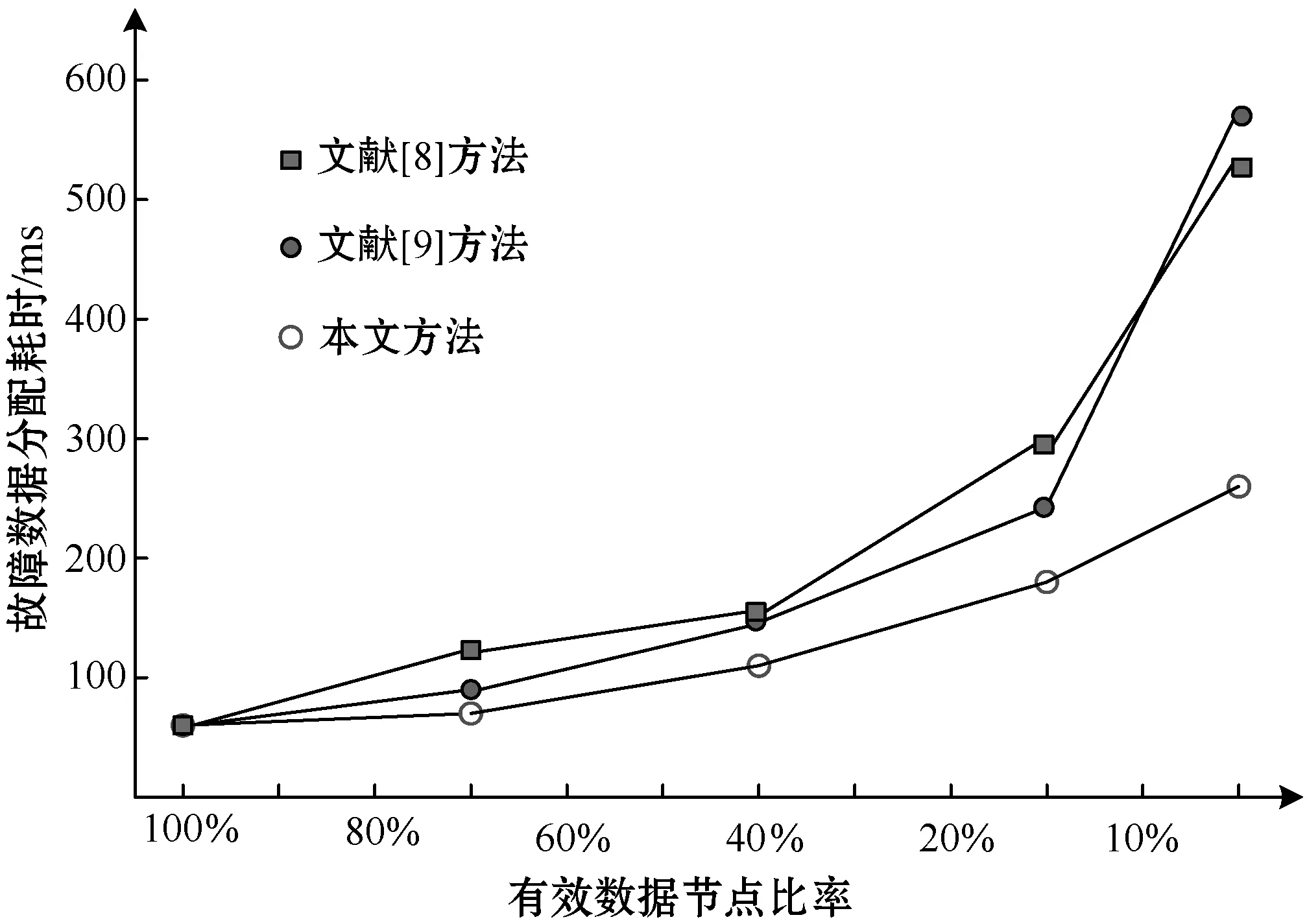
图3 不同预测方法的计算效率对比
可以看出,在同样的有效节点效率条件下本文算法的耗时更少,这主要是由于Spark平台在处理海量故障数据中具有明显的优势,而蚁群算法在全局寻优中也能够选择最短的连接,进而提高故障数据聚类的效率。Aco-k means算法随着有效节点效率的降低,这种计算效率上的优势会越发明显。
算法的复杂度也是衡量滚轴故障检测算法性能的重要指标之一,本文从算法复杂度衡量标准中的时间资源消耗维度出发,分别计算本文算法与文献[7]算法在复合训练样本条件下的故障检测耗时。在相同样本条件下时间资源消耗越多,证明算法越复杂,故障检测时的计算代价越高。具体的数据统计结果如图4所示。
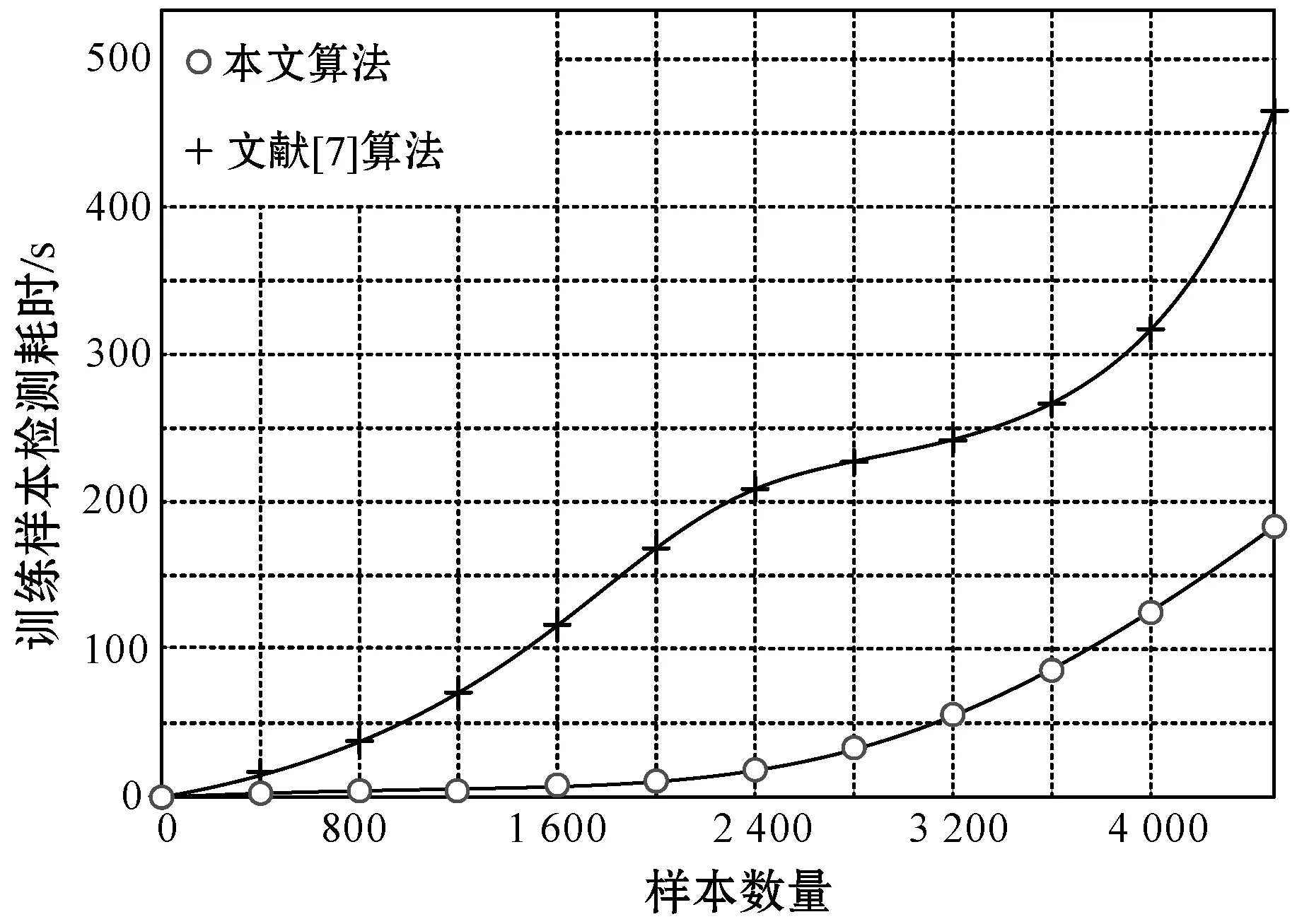
图4 检测算法复杂度的时间维度分析
可以看出,随着样本数量的增加两种算法的时间消耗都在增加,本文检测算法时间资源消耗在每一个节点都保持更低的水平,且变化趋势较为平稳;而文献[7]检测算法在样本值为1 632点和3 745点时出现了波动,单位时间资源消耗开始显著增加。由图4曲线变化趋势可知,本文算法在检测中计算复杂度更低,因此时间资源的消耗更少,同时本文算法的稳定性相对于文献[7]也具有优势,时间资源的消耗更为平稳。
4.3 复合条件下的故障预测准确率对比
旋转设备滚动轴承的故障有可能发生在外圈、内圈、滚子或三者之间的复合状态模式,6种不同的故障状态下生成的训练故障样本与真实故障样本如表3所示。
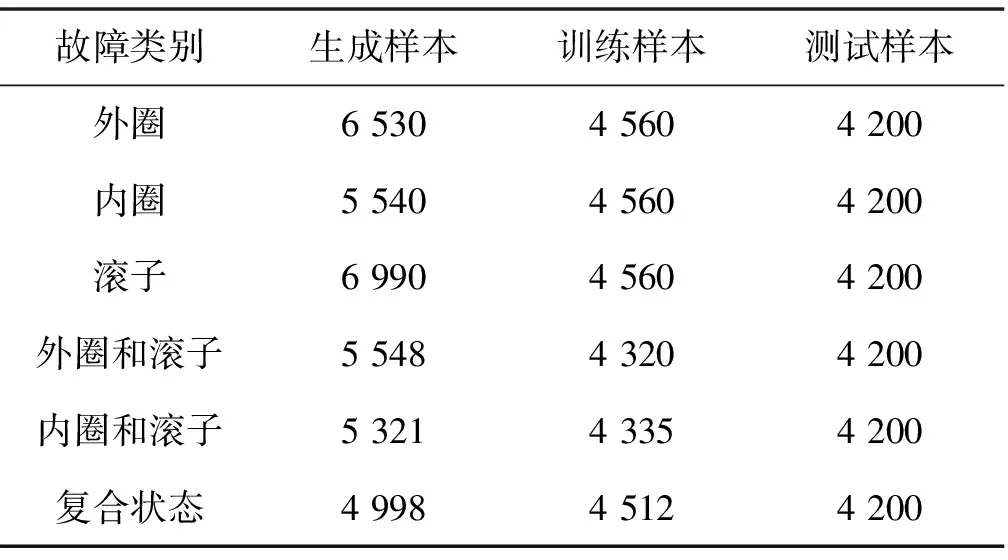
表3 不同故障状态下的测试样本数量
分别验证文献[8]、文献[9]和本文方法对全部6种滚动轴承故障状态下的25 200个测试样本故障检验的准确性,基于MATLAB 8.0软件对全部提取的样本数据故障检测准确率进行分析,6种故障状态下的准确率测试结果如表4所示。
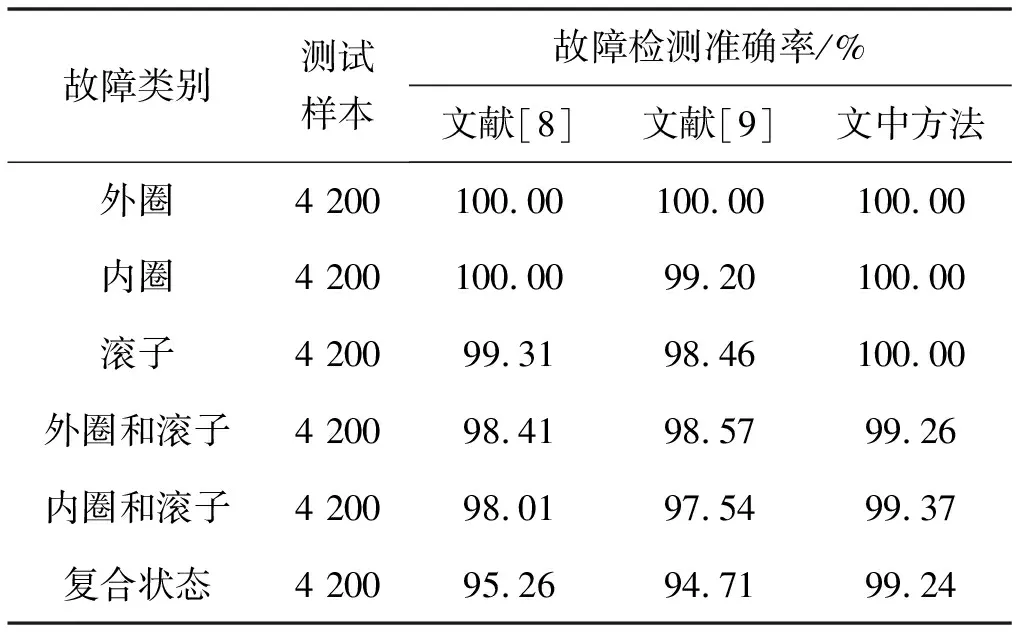
表4 三种故障检测方法的滚轴故障检测准确率对比
从测试样本的分析结果可知,单一故障条件下三种检测方法的故障检测准确率相差不大,但复合状态下本文方法的故障检测率具有明显优势。例如在符合故障状态下,文献[8]方法下的测试样本平均故障检测率为95.26%,文献[9]方法下测试样本平均故障检测率为94.71%,而本文方法的评价故障检测率仍可以达到99.24%。
4.4 不同预测方法下的故障特征提取效率对比
旋转设备滚动轴承的故障提取效率是衡量预测方法有效性的重要指标之一,在故障样本数据集中截取一段样本数量为400,其中训练信号的长度为128,先采用文献[8]和文献[9]的方法诊断是否存在故障信号,检测的频率幅值变化分别如图5和图6所示。
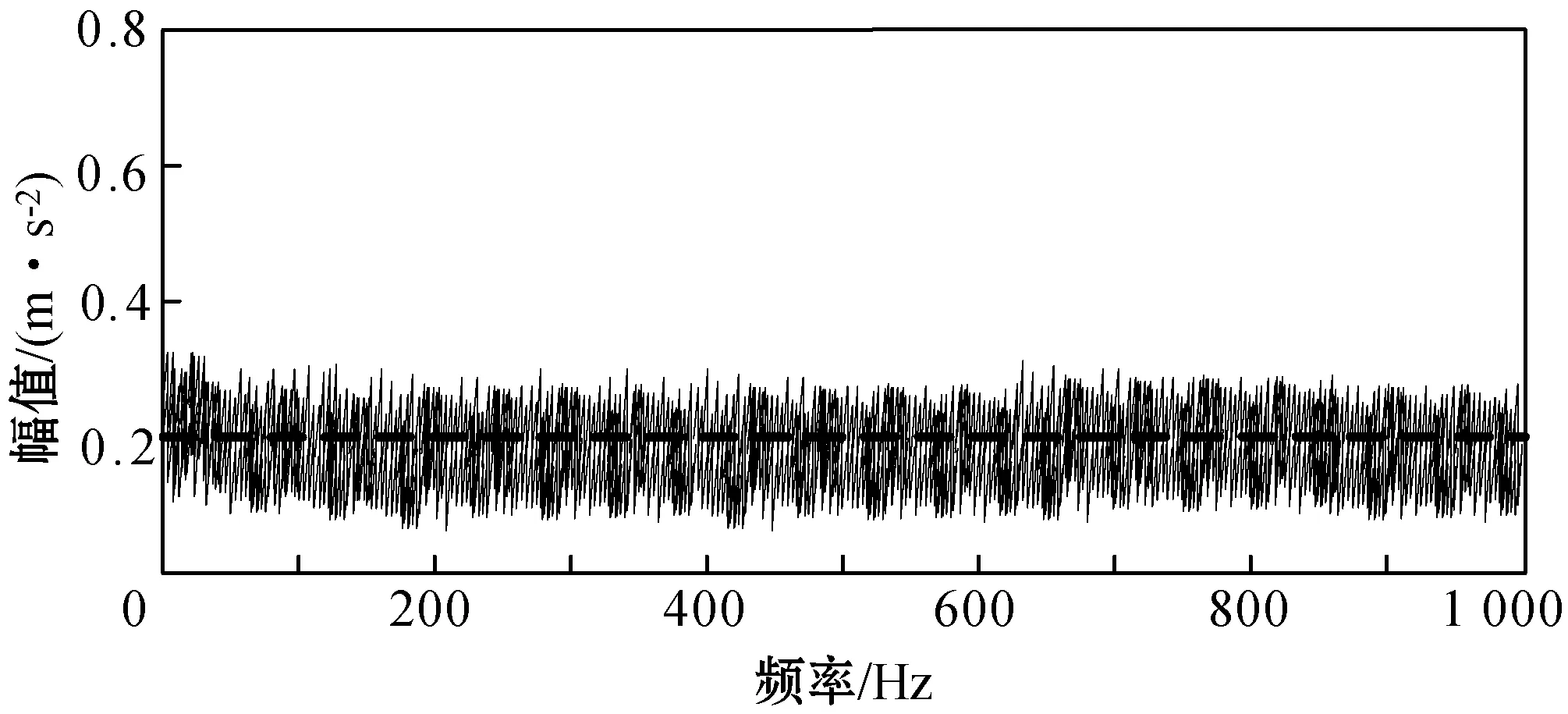
图5 文献[8]方法下的信号解调频谱
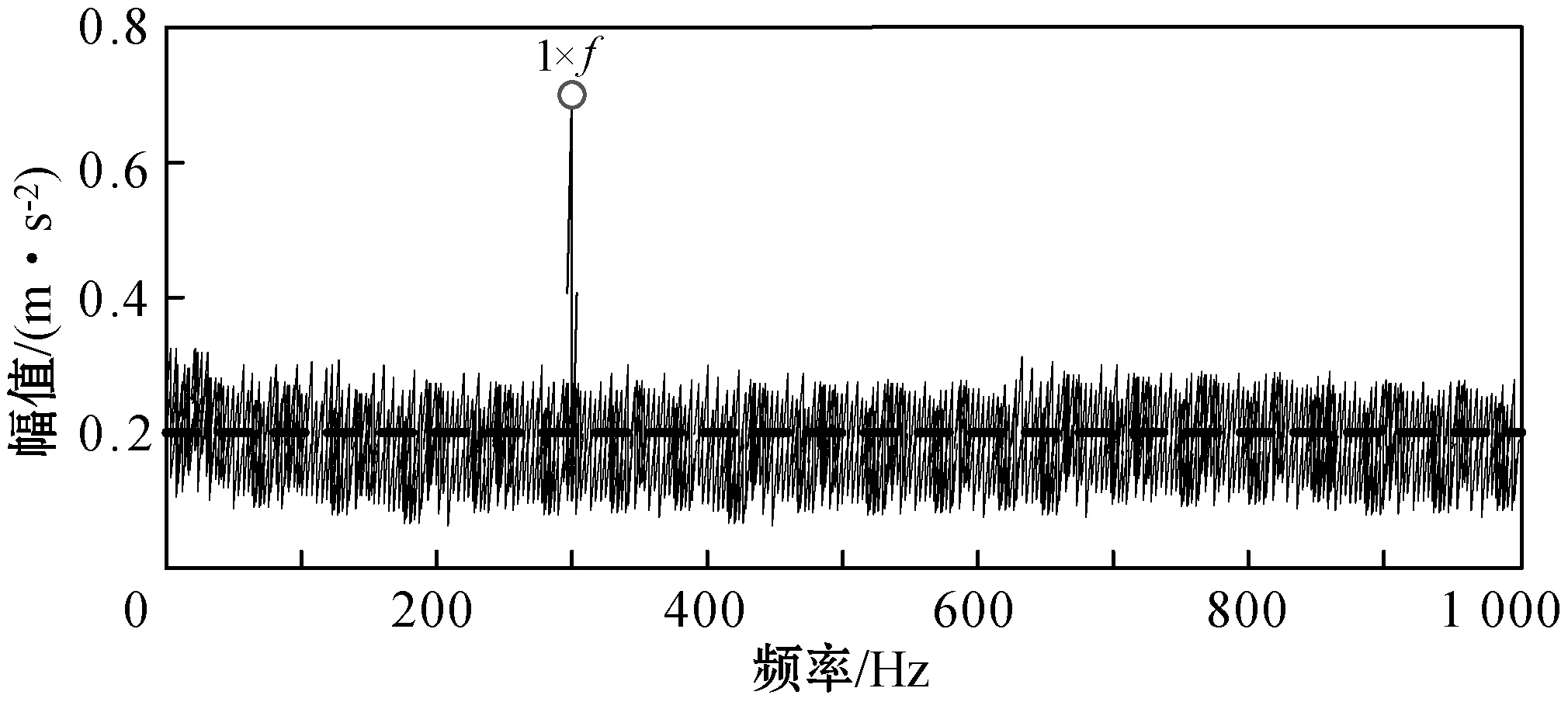
图6 文献[9]方法下的信号解调频谱
可以看出,在文献[8]方法下并未检测出故障样本集中存在信号畸变;而文献[9]方法下识别出了样本集中存在微弱的故障信号。而本文提出的基于Spark平台和Aco-k means算法的滚动轴承预测方法则可以识别出样本集合中存在的全部滚轴故障畸变点,如图7所示。
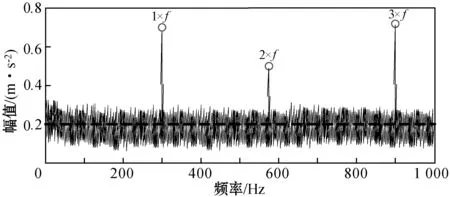
图7 本文方法检测的故障信号解调频谱
可以看出,本文方法的故障特征提取效率要显著优于传统方面,在故障检测方面具有更高的稳定性和可靠性。
5 结 语
本文在大数据环境下提出了一种基于Spark平台和Aco-k means算法的滚动轴承故障数据预测方法,在引入Aco蚁群仿生算法后,能够有效避免传统k means算法存在的局部最优解问题,实现了在全局范围内的滚轴故障集寻优。仿真实验也证明了本文方法的有效性和实用性。
