BH随机邻域嵌入在驾驶行为识别中的应用
2021-01-15杨云开范文兵彭东旭
杨云开 范文兵 彭东旭
(郑州大学信息工程学院 河南 郑州 450001)
0 引 言
驾驶行为分类在过去几年里受到了不同行业的关注。在汽车行业中,对驾驶行为进行分类,对于保证驾驶员的安全至关重要,尤其是在半自动和高度自动化的车辆中。同样,在汽车保险行业,对驾驶行为进行分类和监控对于风险评估和保险费都至关重要[1]。虽然驾驶行为分类是一个有趣的研究主题,但是目前缺乏可用的数据限制了该领域的进展。机器学习技术可以极大地促进研究,但是它们依赖于大量的数据,这些数据可以使用三种不同的方法获得:(1) 驾驶风格问卷:每位驾驶员在自我报告表中评估自己的驾驶行为,但这种方法报告的数据很少,并且会生成主观的度量。(2) 驾驶模拟器:该方法通过对实验条件进行精确控制来模拟驾驶环境,但是环境的人为性质不容易模拟。(3) 真实车辆:真实车辆在日常驾驶过程中采集的数据精度最高,是三种方法中最客观的,在最近的文献中这种方法被称为自然驾驶研究(NDS)[2]。一些代表性的例子如文献[3]中使用100辆车进行研究和最近的公路研究项目(SHRP2)[4]。本文采用第三种方法,使用嵌入不同类型传感器的智能手机在车辆行驶中采集驾驶数据。
通过传感器采集到的驾驶数据往往呈现出高维度和非线性的特点,使用经典的降维算法例如PCA、LDA和LPP等有可能会造成数据特征信息的丢失。t-SNE是目前效果最好的数据降维与可视化方法之一,但是它的缺点也很明显,比如:占内存大,运行时间长。BH-SNE是t-SNE的改进算法,解决了t-SNE计算复杂度和内存复杂度高的问题,而且同样能挖掘高维数据的非线性特性。RBF神经网络能够逼近任意的非线性函数,并有很快的学习收敛速度。因此,本文选择使用BH-SNE来进行降维,使用RBFNN进行分类,并提出一个应用于驾驶行为分类的混合模型:BH-SNE+RBFNN。
1 算法设计
1.1 t分布式随机邻域嵌入
t-SNE最小化了两个分布之间的差异[5]:(1) 度量原始数据对象之间成对相似性的分布;(2) 度量嵌入中对应点之间成对相似性的分布。假设有一个对象的数据集D={x1,x2,…,xN},目标是学习一个s维嵌入,其中每个对象由一个点表示,ε={y1,y2,…,yN},yi∈Rs。为此,t-SNE定义了联合概率pij,通过对两个条件概率进行对称,来度量对象xi和xj之间的成对相似性,计算式为:
(1)
(2)
式中:高斯核δi的带宽设置使得条件分布Pi的复杂度(perplexity)等于预先确定的u(u是一个正整数)。δi的最佳值随对象的不同而变化,并使用简单的二进制搜索找到。在嵌入过程中,利用重尾(Heavy-tailed)分布来测量yi和yj两个对应点之间的相似性qij,计算式为:
(3)
式中:yl和yk为集合ε中任意两点。
嵌入点yi的位置通过最小化联合分布P和Q之间的Kullback-Leibler(KL)距离来确定,计算式为:
(4)
这个代价函数是非凸的,它通常通过沿梯度下降方向来最小化,代价函数梯度计算式为:
(5)
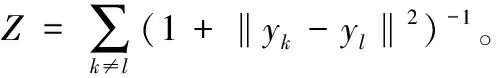
1.2 Barnes-Hut随机邻域嵌入
BH-SNE使用优势点(Vantage-point)树[6]对原始数据对象之间的相似性进行稀疏近似计算,然后使用巴恩斯哈特(Barnes-Hut)算法[7]对嵌入过程中各点之间的力进行近似计算,该算法通常被天文学家用来执行n体模拟。Barnes-Hut算法通过利用一组点对一个相对较远的点施加的力都非常相似这一事实,减少了需要计算的成对力的数量。
由于输入相似性是使用归一化高斯核计算的,所以不同输入对象i和j对应的概率pij(几乎)是无穷小的。因此,对概率pij使用稀疏逼近时不会对最终嵌入的效果产生负面影响。通过找到N个数据对象中每个对象的最邻近的|3u|个对象来计算稀疏近似值,并将成对相似性pij重新定义为:
(6)
式中:Ni表示xi的|3u|个近邻的集合;δi被设置为使得条件分布的复杂度等于u。通过在数据集上构建一个优势点树,可以找到最近邻集Ni。
为了近似计算t-SNE的梯度,将梯度分成如下两部分:
(7)
式中:Fattr为所有引力之和;Frep为所有斥力之和。计算Fattr比较容易,效率也很快,因为它可以通过对稀疏分布P中的所有非零元素求和来实现。由于Frep的计算并不容易,且费时,所以本文采用Barnes-Hut算法来有效地逼近Frep。
1.3 径向基函数神经网络
RBFNN是基于函数逼近理论建立的一种前馈网络,它比BP网络具有更好的函数逼近性能、更简单的结构和更快的训练过程。RBFNN是一个包括输入层、隐藏层和输出层的三层网络[8]。
在RBFNN中,输入层由源节点组成,隐藏层提取输入数据中的聚类特征。从输入层到隐藏层的变换是非线性的,从隐藏层到输出层的变换是线性的。隐藏层的传递函数为径向基函数,是局部分布的中心点径向对称衰减非负非线性函数。
基函数的形式多种多样,但最常用的是高斯函数,因此隐藏层神经元的输出如下:
(8)
式中:x={x1,x2,…,xNi}是具有Ni维度的输入特征向量;ci是第i个高斯函数的中心;Nh是隐藏神经元的数量;δi是RBF隐藏神经元的宽度。
(9)
式中:λ是重叠系数。整个RBF的输出是所有隐藏神经元输出的线性组合,定义为:
(10)
式中:wi为神经网络的权重。
2 识别模型
使用t-SNE算法能很好地挖掘高维数据的非线性特性,且可以将其高维空间数据的内在结构在二维空间内显示出来,揭示数据内在的分类特点,并通过数据可视化直观地表达数据间的相似性。但是t-SNE的计算复杂度和内存复杂度为数据量n的平方,这使得t-SNE只适用于数据量低于几千个点的数据集,一旦数据集过大,t-SNE的处理速度会变得非常慢,降维结果也会变差。驾驶数据集的数量特别大,显然t-SNE并不适用于驾驶行为分析。BH-SNE是t-SNE的改进算法,它只需要O(NlogN)的运算和O(N)的内存,能处理大量的数据集,而且BH-SNE同样能挖掘高维数据的非线性特性。因此本文选择使用BH-SNE进行降维。RBF神经网络能够逼近任意的非线性函数,可以处理系统内难以解析的规律性,具有良好的泛化能力和很快的学习收敛速度,而且不需要调整各种超参数,所以本文选择使用RBFNN进行驾驶行为分类。识别模型的结构如图1所示。
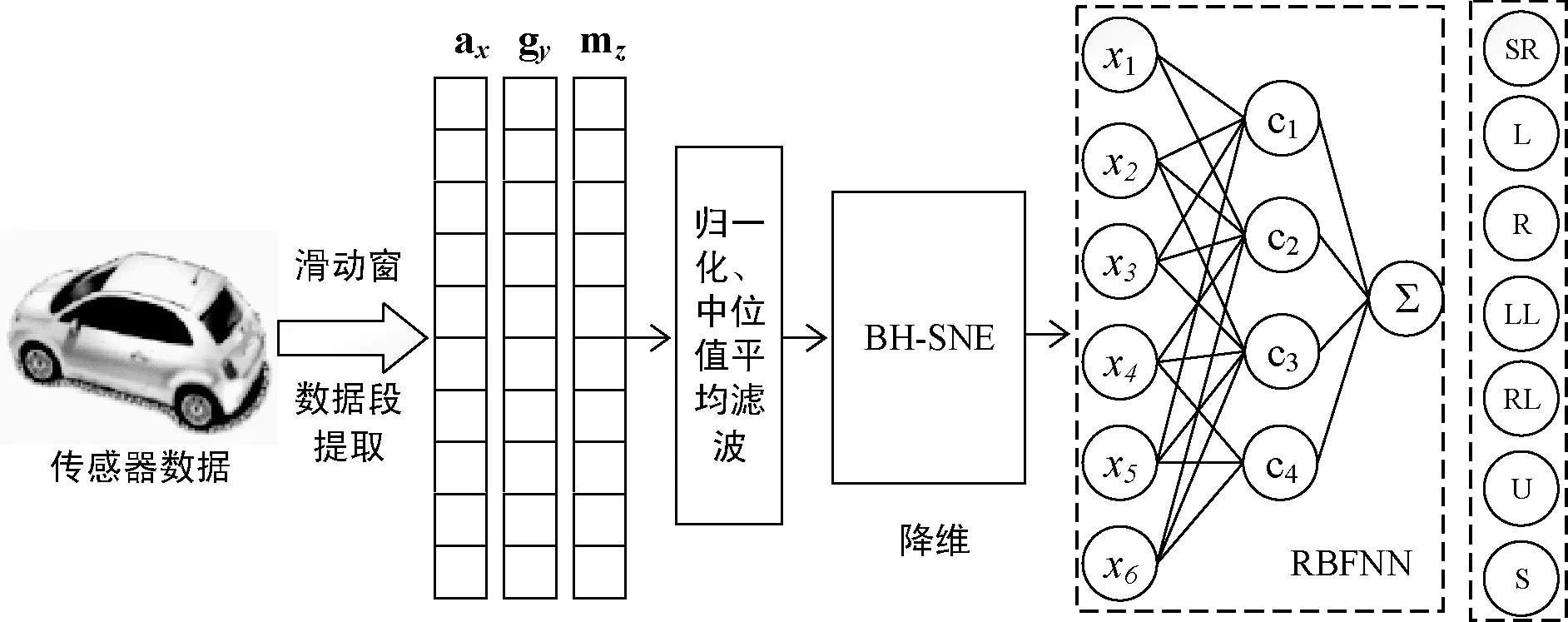
图1 基于BH-SNE和RBFNN的识别模型
可以看出,该模型自左向右由三个模块组成,分别如下:
(1) 数据预处理:使用滑动窗口来提取数据片段,数据片段为一个250×3的矩阵,再将此矩阵归一化并使用中位值平均滤波器去除噪声干扰,最后得到输入样本V{ax,gy,mz}。
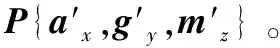
(3) 分类识别:将特征矩阵P输入RBFNN,识别出直线行驶、左转、右转、起步、停车、掉头和静止这七种驾驶行为。
算法流程进一步解释了该模型的实现细节:
输入:三种传感器数据。
输出:七种驾驶行为的概率值。
步骤1数据预处理得到样本V{ax,gy,mz}。
步骤2将ax、gy、mz依次输入到式(6)得到高维空间中的条件概率pij,低维空间中的模拟数据集ε={y1,y2,…,yN},对ε进行数据初始化,将ε代入式(3) 得到低维空间中的条件概率qij。
步骤3将pij和qij代入式(4)得到代价函数C。
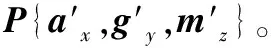
步骤5初始化聚类中心ci,确定基函数的个数,不断地调整ci直到不再变化,初始化权值wi。
步骤6将ci代入式(9)得到δi,将δi代入到式(8)得到Ri(x),最后将Ri(x)和wi代入式(10),输出当前样本在各个类别下的概率。
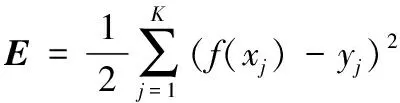
3 数据预处理
3.1 样本数据选择
过去大多数驾驶模式识别系统只使用加速度计的数据。本文决定使用加速度计、陀螺仪和磁力传感器的传感器融合输出来检测和识别驾驶运动。因为陀螺仪测量的是车辆的转向加速度,所以可以用来检测车辆转弯运动,而磁力传感器可以检测到车辆行驶方向的磁感性强度,每个方向的磁感性强度都是固定的,当车辆行驶方向变化时磁感性强度也随之改变(相当于一个罗盘)。三者配合使用,可以更准确地读出车辆的姿态(方向)。本文采用的陀螺仪、加速度计和磁力传感器可以测得运动物体三个坐标轴上的分量,假设这三个传感器测得的数据分别为G={gx,gy,gz} rad/s,加速度计值A={ax,ay,az} m/s2,设备磁力传感器M={mx,my,mz} μT。
本文使用ax、gy、mz作为样本数据进行分类,因为在A、G、M中只有这三个单轴数据能反映车辆方向的变化。认为集合T={ax,gy,mz}是区分驾驶行为的最佳信号选择。最后使用中位值平均滤波法对集合T进行滤波处理,滤除由偶然因素所引起脉冲性干扰致使的数据突变。
3.2 提取数据片段
获取到集合T的数据后,提取n个样本数据段。数据段的数量取决于所涉及的应用的类型。增加段的长度可以提高识别精度,但同时会使不同活动之间的边界变得不那么清晰。综合考虑本文采用10 s的非重叠窗口大小对原始惯性时间序列数据进行分割(几乎所有的驾驶行为如转向、起步、停车和掉头等都能在10 s内完成)。使用分段而不是单个数据点的原因是原始惯性测量的高度波动使得单个数据点的分类不切实际。因此,使用分别应用于ax、gy、mz轴上的滑动窗口来获得数据片段[9]。在25 Hz的数据采集频率下,250次数据作为一个数据段,将这个250×3的矩阵V{ax,gy,mz}作为识别模型的输入样本。
4 实 验
4.1 实验数据集
本文是以内置ARM处理器的智能手机作为驾驶行为数据采集硬件。智能手机使用配置了线性加速度传感器和陀螺仪以及磁力传感器的荣耀V10和iPhone 6S。智能手机被水平地放置在汽车仪表盘中间位置,x轴与仪表盘平齐,y轴垂直地面向上,z轴面向前进方向。汽车平台为起亚赛拉图和雪佛兰赛欧3,数据收集软件为phyphox(一个国外的传感器数据测试软件),实验采集了4名用户的驾驶行为数据,分别为直线行驶(SR)、左转(L)、右转(R)、起步(ST)、停车(P)、掉头(U)和静止(S)。采样频率为25 Hz,共收集了超过2 800份样本数据,如表1所示。
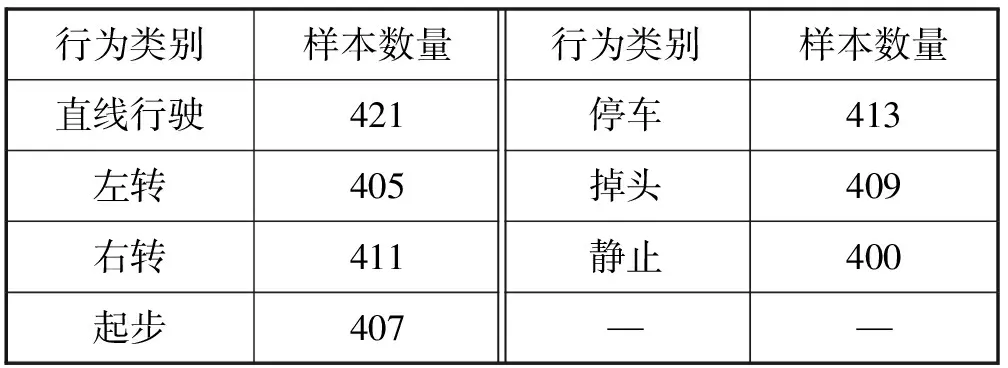
表1 实验数据集
4.2 参数设置
整个实验过程在MATLAB 仿真环境中进行。把实验数据分成三份:60%的训练集,20%的交叉验证集,20%的测试集。
BH-SNE算法的参数设置[10]:从方差为10-4的高斯函数中采样来初始化嵌入点。1 000次迭代梯度下降一次,初始步长设置为200。复杂度设置为30。所有维数大于50的数据集都使用PCA进行预处理,将维数降为50。
RBFNN模型的参数设置:径向基函数的扩展(spread) 设置为1,中心点的个数设置为7。
4.3 实验对比与结果分析
实验1探讨t-SNE与BH-SNE在降维方面的优劣,将集合T的三个数据集A、G和M分别输入t-SNE与BH-SNE进行降维,将数据从250维降到2维并显示在二维坐标中,可视化结果如图2所示。
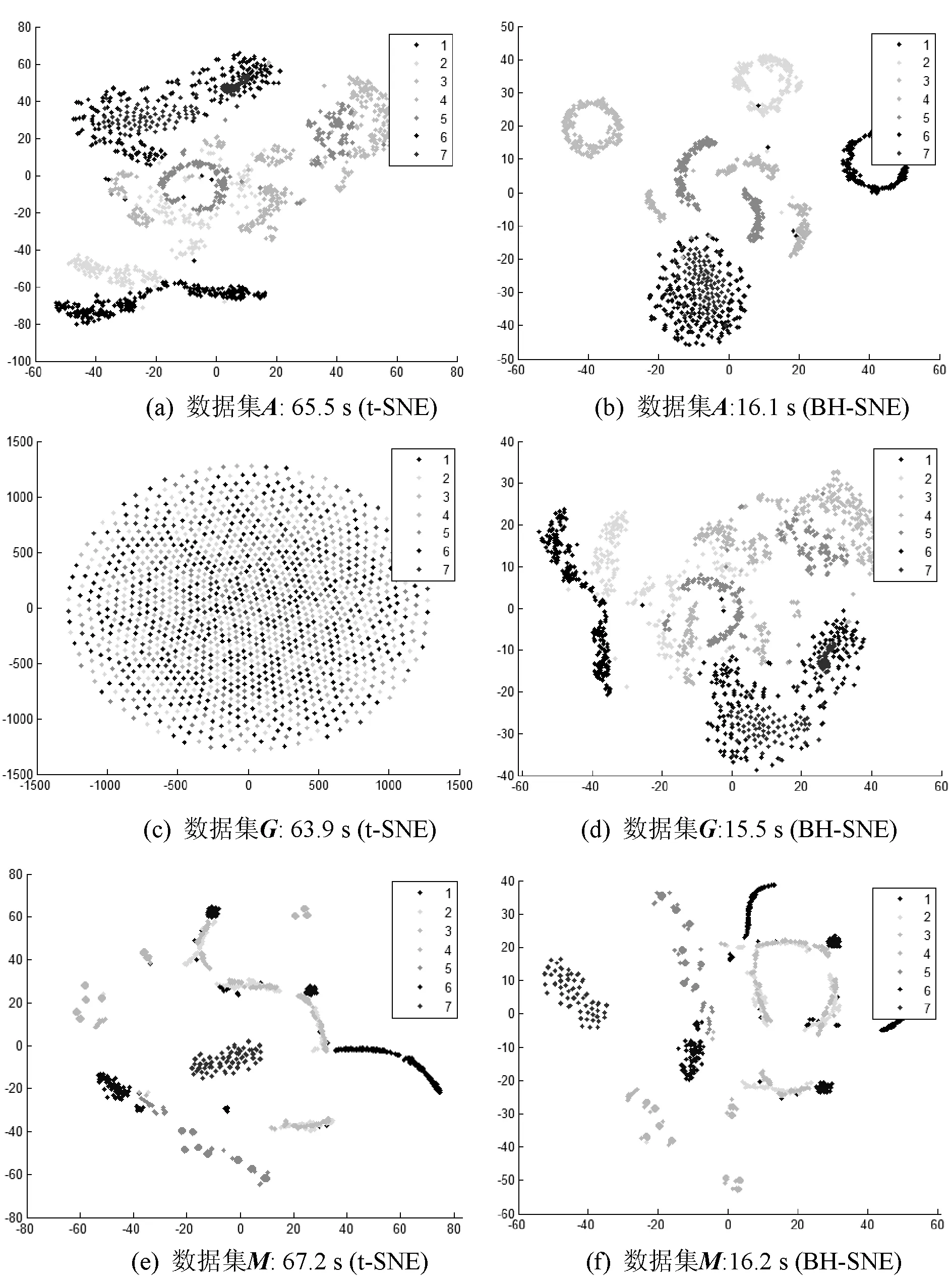
图2 t-SNE与BH-SNE的可视化效果对比
图2中,点的颜色(灰度表示)对应驾驶行为的类别可以看出,BH-SNE可以构建高质量的传感器数据嵌入。由图2(c)可以看出,数据集G的可视化效果非常差,表明t-SNE不能很好地提取数据集G的特征,而图2(d)的可视化效果非常好。同时在数据集A和M上,使用BH-SNE和t-SNE的可视化效果相差不大。综合对比,BH-SNE的可视化效果比t-SNE好,因此BH-SNE的驾驶行为数据特征提取能力比t-SNE更好,而且从计算时间上可以看出,BH-SNE的效率远高于t-SNE。综上可以说明BH-SNE比t-SNE更适用于驾驶行为研究。
实验2探讨使用BH-SNE进行降维的原因,将输入数据T分别用自编码器(AE)、主成分分析(PCA)、线性判别分析(LDA)、局部保持投影(LPP)、t-SNE和BH-SNE进行降维,然后将降维数据分别输入到BP神经网络、SVM、AdaBoostM2和RBF网络中进行分类,结果如表2所示。
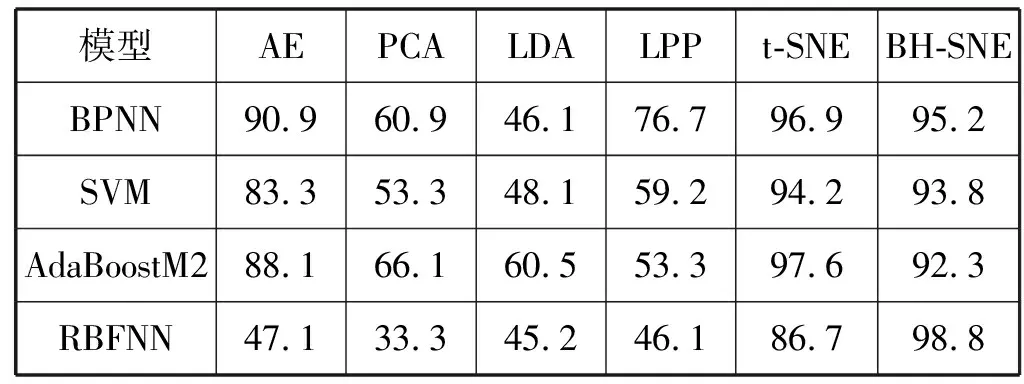
表2 不同降维模型的降维效果对比
可以看出,t-SNE和BH-SNE的降维效果要优于其他降维算法,其中t-SNE的降维效果要优于BH-SNE,但是t-SNE的运行速度太慢,且t-SNE和RBFNN结合的分类效果并不好,所以本文选用BH-SNE进行降维。t-SNE+RBFNN模型的具体识别结果如表3所示。
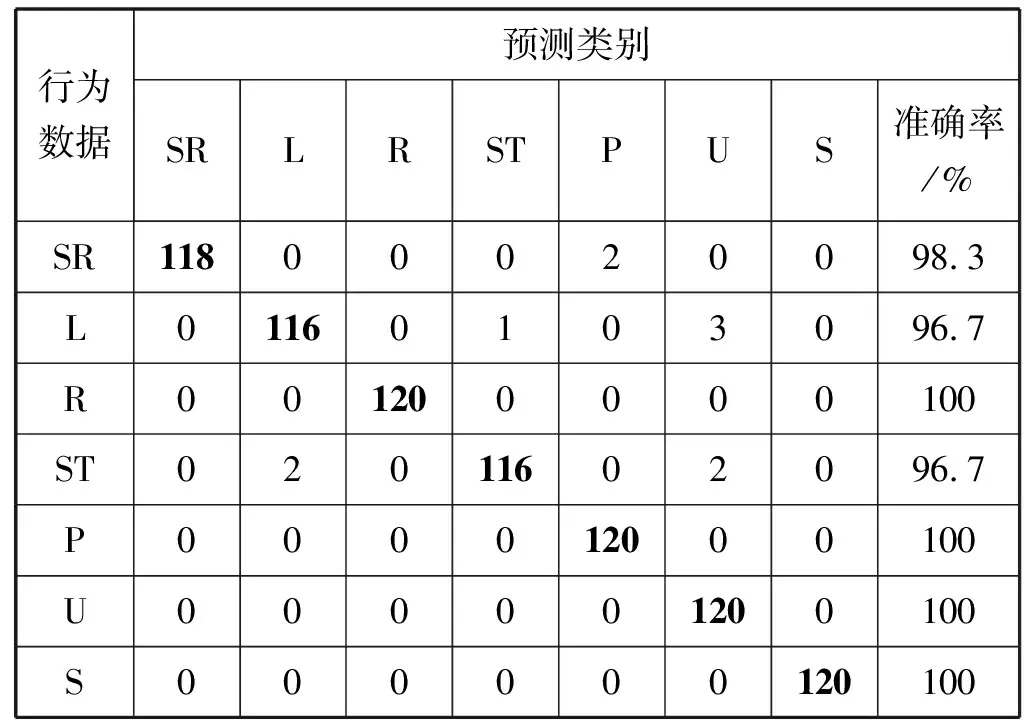
表3 具体识别结果
实验3将BH-SNE+RBFNN模型与两个传统的机器学习识别模型进行对比,比较结果如图3所示,可以明显地看出本文提出的模型识别效果最好,其他两个模型平均识别率最高的是BP神经网络的84.2%。同时将本文的模型与新型的分类模型Deep Forest(深度森林[11])进行对比,本文的模型识别效果更好。
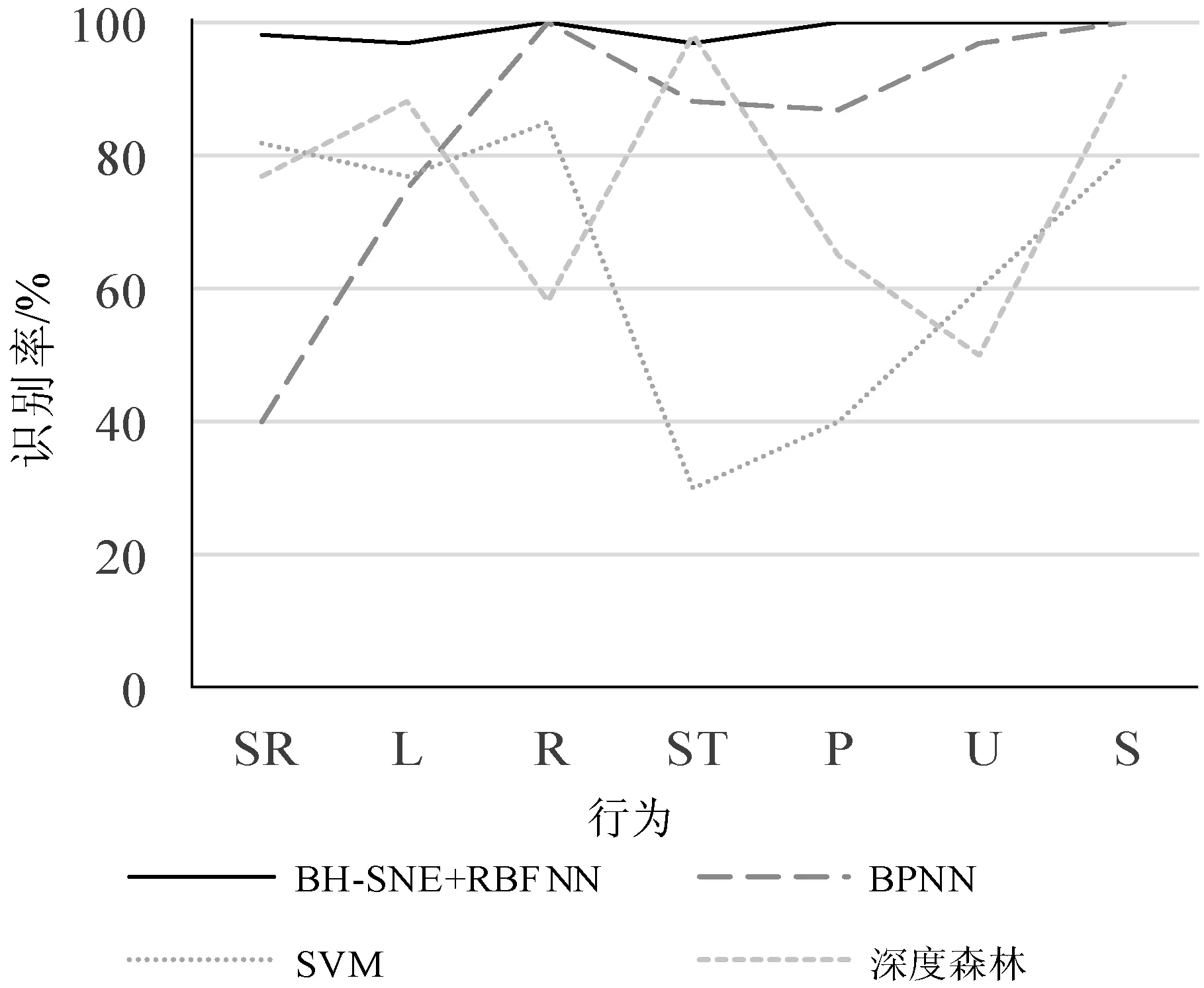
图3 常见分类模型识别效果对比
5 结 语
本文提出一种BH-SNE结合RBFNN的模型,用于识别常见的驾驶行为,包括纵向和横向运动。该模型不仅比其他分类算法具有更好的分类效果,而且能有效地处理和识别实时序列数据。BH-SNE不仅实现了降维的效果,还能通过可视化观察数据的特性。RBFNN的分类效果很优秀,而且运行速度很快。实验结果也验证了该方法的有效性和可行性,且对汽车安全行驶具有实际应用价值。
